高层建筑钢斜交网格筒结构地震易损性分析

方登甲，刘成清，杨鲸津

(西南交通大学 土木工程学院，四川 成都 610031)

3T(twisted，tilted，& tapered)设计[1]作为一种结构设计元素为实现不同长细比要求的世界各地标志性摩天建筑提供了可能性。3T设计元素塑造的新型结构之一——斜交网格结构，因其外观如镶嵌宝石般展现出简洁、直挺的建筑美而在近些年迅速风靡全球。Volner甚至提到高层建筑无疑已是进入斜交网格结构的时代[2]。近20年来，已经有许多文献研究了斜交网格结构的初始设计方法、抗震性能、抗连续倒塌能力、剪力滞后、平面立体几何形状的优化、节点连接以及试验研究等[3-4]。为了提高高层建筑斜交网格结构的性能，基于性能的结构抗震思想也被逐渐运用于斜交网格结构的设计和评估。性能设计目标通常侧重于提高结构的承载能力而推迟结构进入塑性变形[5]。由于地震的随机性和不确定性，基于性能的结构分析与评估应建立在概率基础上[6]。结构地震易损性曲线直接受性能水平的极限状态限值的影响，对于传统结构可以根据规范以及现有研究结果可以参考取值，而对于斜交网格结构因其侧向刚度较大，性能水平的极限取值很难决定。已经有学者提出方法来确定传统结构的性能水平极限状态限值，如张令心等[6]所提出的通过增量动力分析曲线的斜率判断性能水平的方法对于传统超高层混合结构的易损性评价有很高的准确性，而对于钢结构有时候因出现结构刚度硬化就可能不好做出判断；尹建华等[7]也提出基于形态点的取值方法，但对于斜交网格结构的适用性有待于进一步研究。斜交网格结构构件的塑性铰成形顺序是一个值得的研究课题之一，塑性铰开展可以演示结构渐进破坏的过程。刘晶波等[8]通过描述结构的极限破坏状态确定了性能化指标限值，可以准确评价钢管混凝土框架的易损性，但是此方法只仅限于通过第1层结构的破坏来定义整体结构性能的指标限值。

高层斜交网格结构形式往往是筒中筒结构体系，分外内筒和外筒，内外筒之间的剪力分配和地震作用下的剪力流向均影响结构的性能状态的变化和抗震性能。因此，本文通过静力弹塑性分析方法确定了斜交网格筒中筒结构(以下简称斜交筒)的性能水平及其极限状态限值，并以此对结构进行了易损性评价。在此过程中，建立与斜交网格筒总用钢量相同的框架筒中筒结构(以下简称框架筒)来做对比分析。

1 双重抗侧力结构体系

筒中筒结构的外周框架(或外周斜交网格筒)与内筒的相对强弱对结构的内力分配、抗震性能以及抗连续倒塌性能等有着密切联系。为分别讨论结构中框架筒和斜交网格筒的结构易损性的准确评估，本文以百米级高层建筑为例，用ETABS软件设计基于总质量及内外筒总用钢量相等原则的框架筒和斜交网格筒，并用有限元Perform-3D进行数值建模和非线性分析。

为能够清楚简洁地表征框架筒及斜交网格筒结构二者双重抗侧力体系的区别，研究对象为筒中筒结构，两结构平面均为30 m×30 m的矩形，结构总高度100.8 m，高宽比3.36，层高均为3.6 m。抗震设防烈度为8度(0.2g)，场地类别为Ⅱ类场地，设计地震分组为第2组，场地特征周期0.4 s。两结构的梁和柱构件均为钢结构，钢材为Q345，板构件采用板厚为150 mm的C30混凝土。楼面均布恒载、活载均取3 kN/m2。框架筒与斜交网格筒结构模型见图1。构件截面具体尺寸见表1。斜交网格筒结构的总重比框架筒结构的大0.18%，两结构总质量接近相等。斜交网格筒结构的基本周期比框架筒的小33.62%。

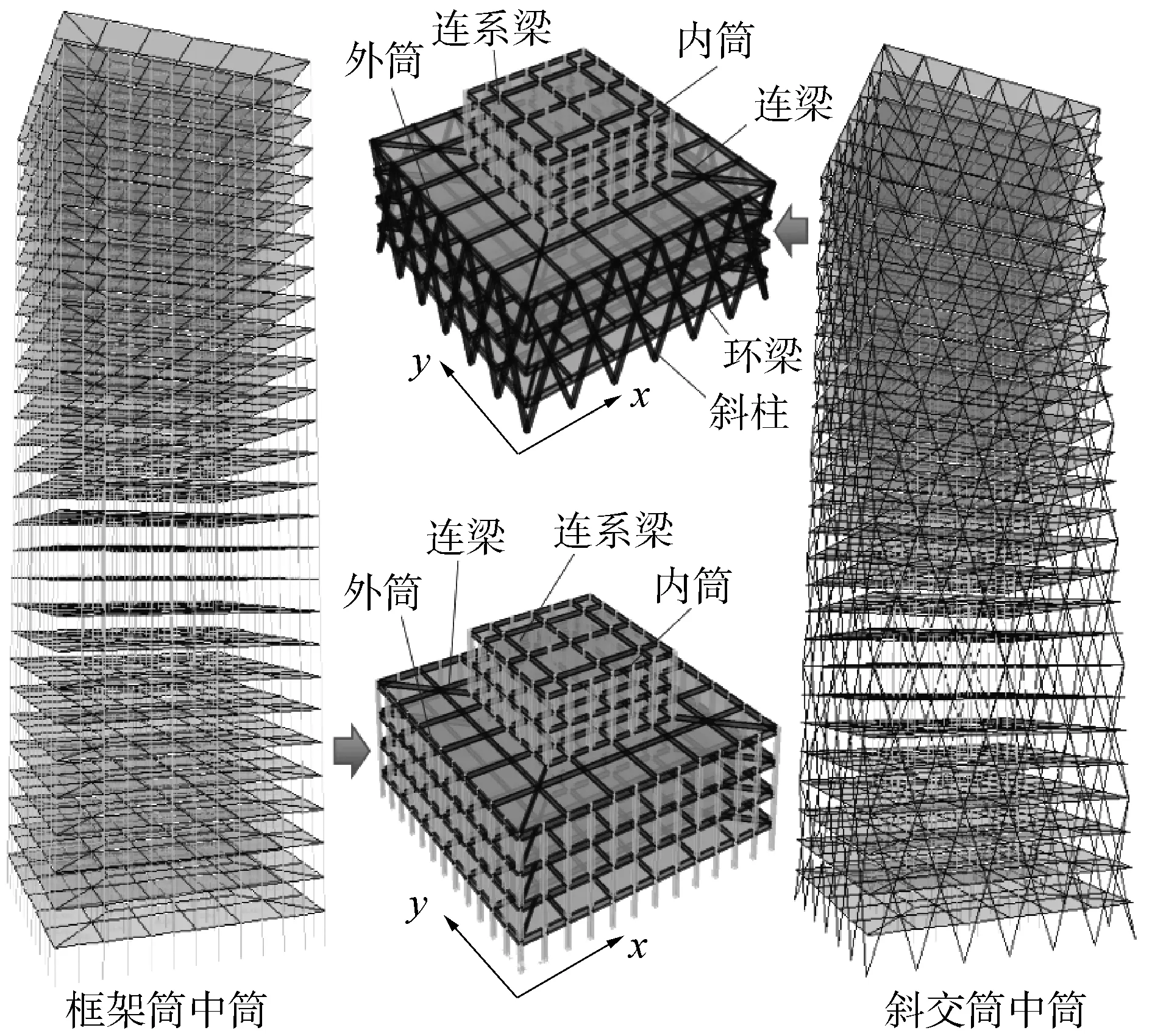
图1 框架筒与斜交网格筒结构模型

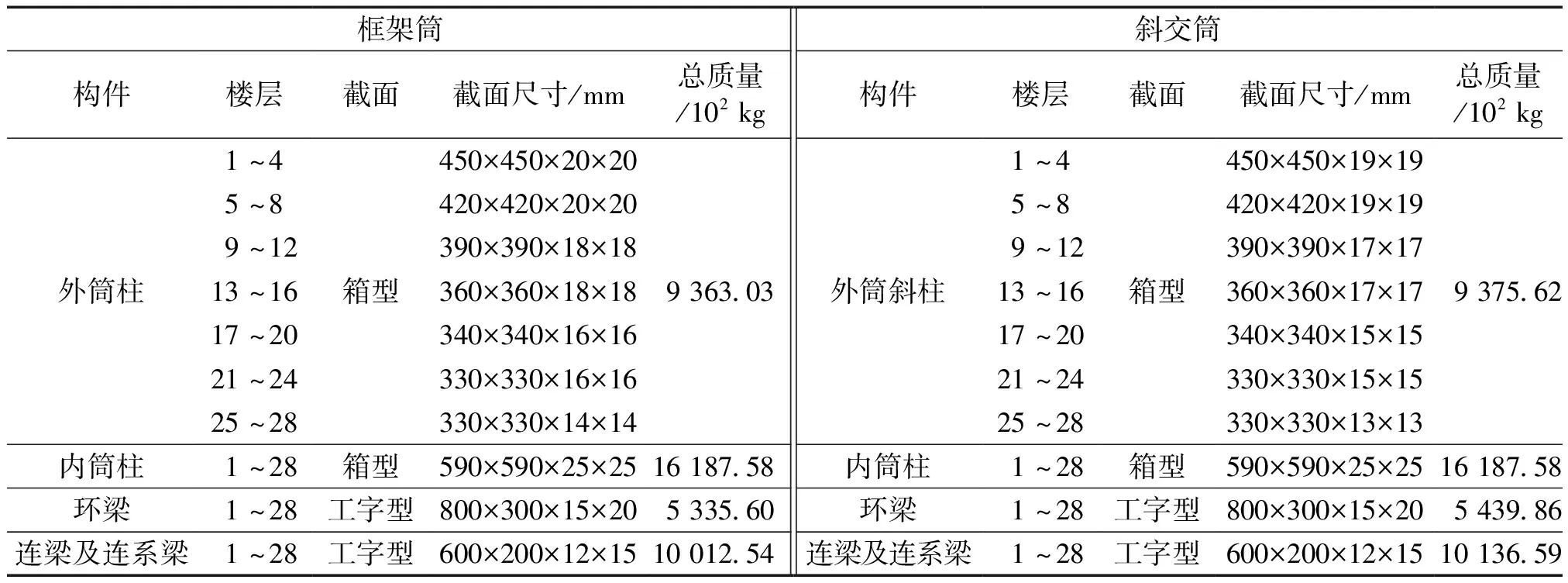
表1 构件截面信息

采用三维非线性分析软件Perform-3D的纤维模型进行非线性分析。钢材采用考虑应变硬化的三线性弹塑性模型，强屈比取1.2，极限受拉应变值取10倍的屈服应变值。按技术规程[9]的第5.4.6条规定，结构阻尼比在多遇地震取0.03，罕遇地震取0.05，计算时考虑P-Δ效应。采用纤维截面对数值模型中梁(连系梁、环梁)和柱(斜柱)的塑性特征进行模拟，梁柱构件单元由两端设置塑性区和中间弹性杆组成，并定义梁柱纤维截面的塑性区。假设所有节点均为刚接，采用平截面假定和刚性楼板约束。刚性楼板的水平质量和水平转动质量按ETABS的分析结果输入，构件和节点上的荷载按ETABS设计换算后的荷载值输入。

2 结构性能量化指标确定方法

2.1 量化指标限值的确定

衡量结构抗震性能水平的标准直接关乎结构最终的评价结果，同时也影响地震易损性曲线的形状和结构性能水平的超越概率。结构性能水平定义的实质是对结构破坏状态的预期确定。本文按通常划分习惯将其划分为“正常运行”、“立即使用”、“生命安全”、“防止倒塌”4个性能水平。量化指标限值是定义结构破坏状态的物理极限状态值LSi。因本文研究对象均为筒中筒结构，结构的变形比构件承载力能更好地反映结构整体的性能，选用最大层间位移角θmax作为量化指标来衡量结构的破坏状态相对更加合理。采用一阶模态的倒三角形侧向力分布对结构进行静力弹塑性分析。图2(a)所示为结构的推覆方向和塑性铰在其所对应荷载-位移曲线上的位置。图中B点为屈服点，IO为立即使用，LS为生命安全，CP为防止倒塌，C为失去极限承载力。以设置在承重构件上的塑性铰出现B定义为“正常运行”性能上限值LS1；以塑性铰出现IO定义为“立即使用”性能上限值LS2；以塑性铰出现LS定义为“生命安全”性能上限值LS3；以塑性铰出现C定义为“防止倒塌”性能上限值LS4。根据Pushover分析过程中塑性铰状态的变化及其所得Pushover曲线，将分析中结构各个塑性铰状态出现时所对应的水平层间位移角标注在曲线上，以确定性能水平极限状态的量化指标限值。

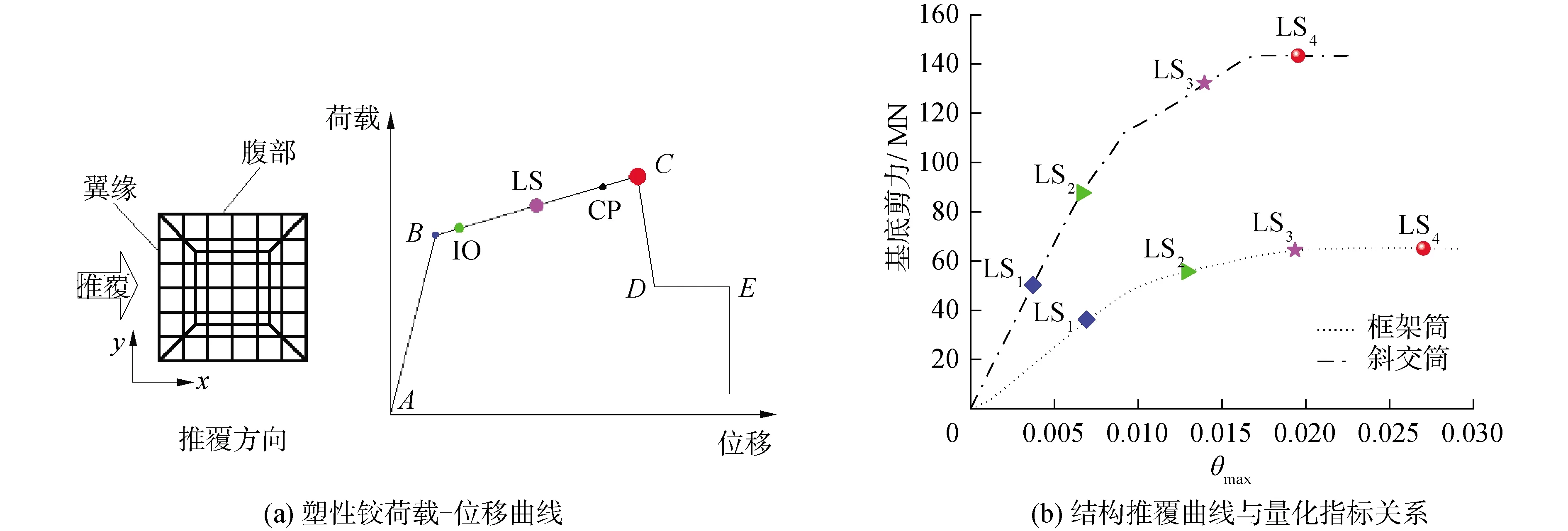
图2 性能水平量化指标限值

图2(b)给出了Pushover分析得到的结构基底剪力-层间位移角关系曲线及相应的量化位移指标限值LSi，斜交筒的水平承载力和侧向刚度要明显大于框架筒，斜交筒结构推覆曲线的初始刚度是框架筒的2.82倍。最终确定的各性能水平下的斜交筒量化指标限值总比框架筒要小，斜交筒量化指标限值LS1、LS2、LS3和LS4分别是框架筒的0.54倍、0.52倍、0.72倍和0.73倍。

2.2 塑性铰开展特点

图3(a)和(b)分别为框架筒和斜交筒在“生命安全”和“防止倒塌”性能所对应的塑性铰分布，以示2个结构塑性铰开展演化的典型差别。为了清楚显示塑性铰的分布及演化过程，仅以底部4层结构来表征。可以明显看出2个结构破坏过程的不同。框架筒结构的破坏过程以外筒腹部的底部各楼层柱脚和内筒连系梁的塑性铰开展为主，在结构倒塌之前主要由内筒的连系梁屈服耗散地震能量。内筒连系梁最终失去极限承载力的位置出现在第2层，而非第1层。因此，文献[8]中仅以第1层结构的塑性铰开展来定义量化限值的方法可能只是适用于高度较低的结构，对百米级建筑的应用可能就有了局限性。框架筒翼缘部的破坏则主要是以底层柱柱脚的破坏为主。腹部内外筒的塑性铰开展方向则由中间向两端角部位置以及由底层向更高楼层开展。

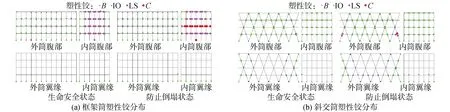
图3 生命安全和防止倒塌性能所对应的塑性铰分布

而斜交筒结构的破坏塑性铰位置分布则完全不同，斜交筒结构的破坏过程主要是外筒底部各层斜柱柱顶、柱脚以及内筒连系梁塑性铰的开展。外筒翼缘部因剪力滞后在两端角部位置塑性铰的开展比较严重。塑性铰开展严重部位并非出现在结构底层。内筒的损伤破坏程度也相对框架筒结构较轻。由此可总结出，框架筒的破坏是以内筒的连系梁为主导的，而且内筒的破坏程度比外筒要更严重。斜交筒的破坏则是以外筒斜柱和内筒连系梁的破坏为主，内外筒同时协同工作的能力较好。

斜交筒结构的破坏机理与框架筒结构的完全不同。表2中描述了不同性能水平下结构所处的破坏状态和其所对应的性能量化指标限值，主要以代表性塑性铰的出现以及结构破坏情况的分布来表达。

表2 性能水平及其破坏状态描述

3 地震易损性分析

3.1 地震记录的选取

地震动的合理选取会影响对结构性能的有效评估。综合考虑我国抗震规范[5]的要求，按照地震反应谱卓越周期与结构所处场地特征周期相近的原则[10]，通过太平洋地震研究中心数据库选取相当于Ⅱ类场地的15条地面峰值加速度(peak ground acceleration, PGA)为0.12g～0.20g的地震记录，地震动有效持时范围为29～59 s。地震加速度反应谱及其设计反应谱曲线见图4。

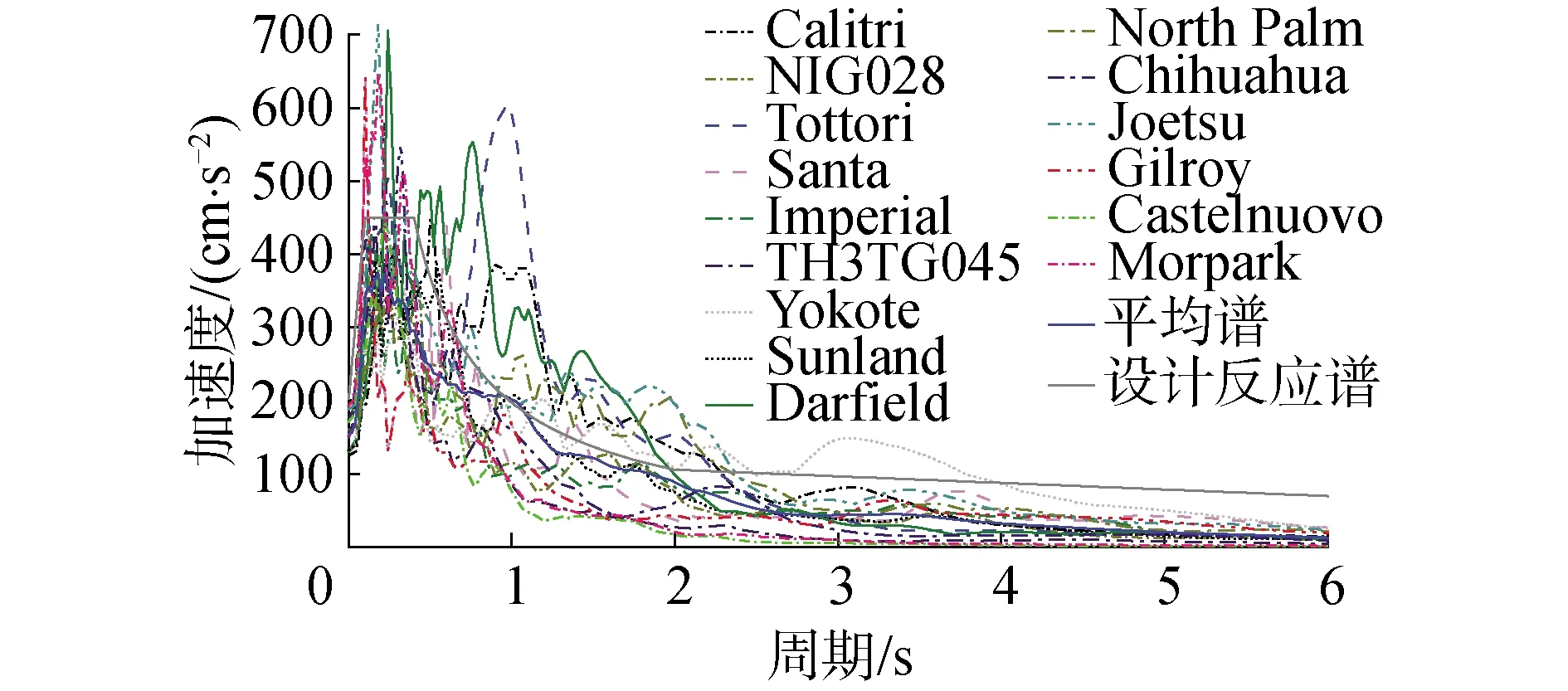
图4 地震波反应谱

3.2 增量动力分析

增量动力分析法(incremental dynamic analysis, IDA)因能对结构进行大量地震作用下的非线性动力分析，反应结构在不同地震作用下的结构响应，从而能对结构做出全面准确的抗震性能评估。将上述15条地震动记录按PGA进行调幅，对每条地震记录以调幅增量为0.1g，从0.1g调幅至1.5g。用每条地震波调幅后的PGA作为输入进行非线性动力时程分析，将计算分析得到的结果进行样条插值处理得到的PGA与最大层间位移角θmax的关系(IDA)曲线如图5所示。

由图5可知，随着地震动强度的增加，框架筒与斜交筒结构的IDA曲线均表现出了由直线向曲线的发展趋势，表明结构从弹性阶段向塑性阶段发展的过程。对比2种结构的IDA曲线可知，斜交结构的IDA曲线相对集中和收敛，这意味着斜交结构的整体性能较好，与框架结构相比，斜交结构采用相对较少的地震波条数就能满足对结构抗震性能的评估。结构在15条地震作用下的IDA曲线表现出较大的离散性，假设IDA曲线服从正态分布。地震动强度参数IM(intensity measure)取地面峰值加速度PGA，结构性能参数EDP(engineering demand parameter)为最大层间位移角θmax。取曲线中某一结构性能参数EDP值所对应的地震动强度参数IM均值μ和对数值标准差δ，所得到的(EDP,μe-δ)、(EDP,μ)、(EDP,μe+δ)3条曲线为结构的16%、50%、84%分位曲线见图6。最大层间位移角θmax均随着PGA的增大而增大，在θmax较小时关系曲线为线性变化。斜交筒结构的初始斜率均比框架筒的大。其中，斜交筒结构的50%分位曲线的初始斜率是框架筒的2.19倍。在分位曲线上可以看到有些位置的切点斜率出现增大，结构出现“硬化”。因此，通过斜率的降低来确定结构的性能点的方法[6]很难做出准确的判断。

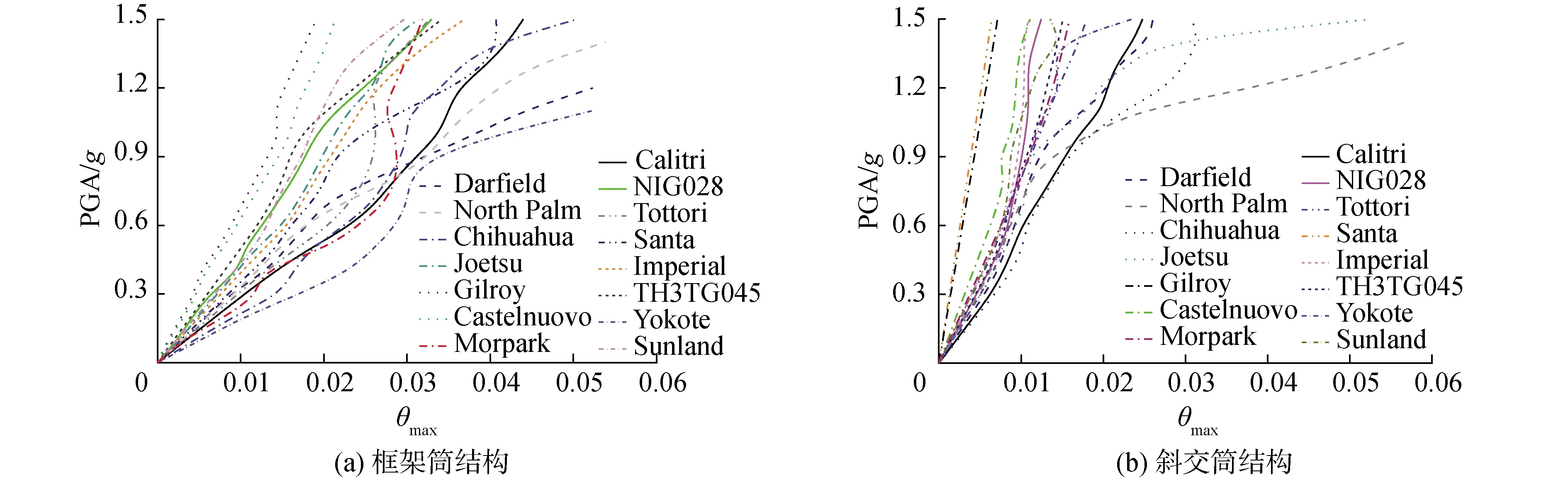
图5 IDA曲线

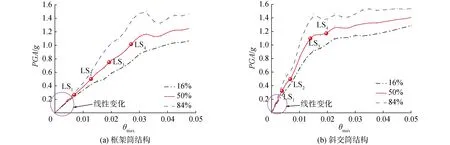
图6 2种结构的16%、50%和84%分位曲线

3.3 概率地震需求分析

概率地震需求分析通过概率方法来统计结构遭受不同强度地震的响应，利用对结构进行多条地震动下的非线性动力时程分析结果，建立概率地震需求模型。常假设概率地震需求分析服从对数正态分布，得出地震需求参数D与地震强度参数IM之间的关系方程。基于2种结构的增量动力分析结果，取峰值加速度PGA的对数值为横坐标，取最大层间位移角θmax的对数值为纵坐标。对2种结构在15条地震波经调幅后的计算数据进行对数线性回归分析。框架筒结构的地震概率需求模型线性回归方程为：

ln(θmax)=0.914ln(PGA)-3.718

(1)

斜交筒结构的地震概率需求模型线性回归方程为：

ln(θmax)=0.917ln(PGA)-4.473

(2)

易损性曲线依据地震动强度参数IM和地震需求参数D来建立，结构达到某一破坏极限状态的概率可用以下公式表示：

FR(im)=P[D≥C|IM=im]

(3)

式中：D表示地震需求参数；C表示结构的抗震性能。参照结构破坏性能的等级划分，式(1)可以表示为：

FR(im)=Pf[LSi|IM]=P[D≥Ci|IM=im]

(4)

式中：Pf表示结构失效概率；Ci表示正常运行、立即使用、生命安全及防止倒塌4个性能；LSi表示结构超过或达到以上4个性能点的极限状态。

(5)

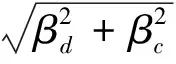
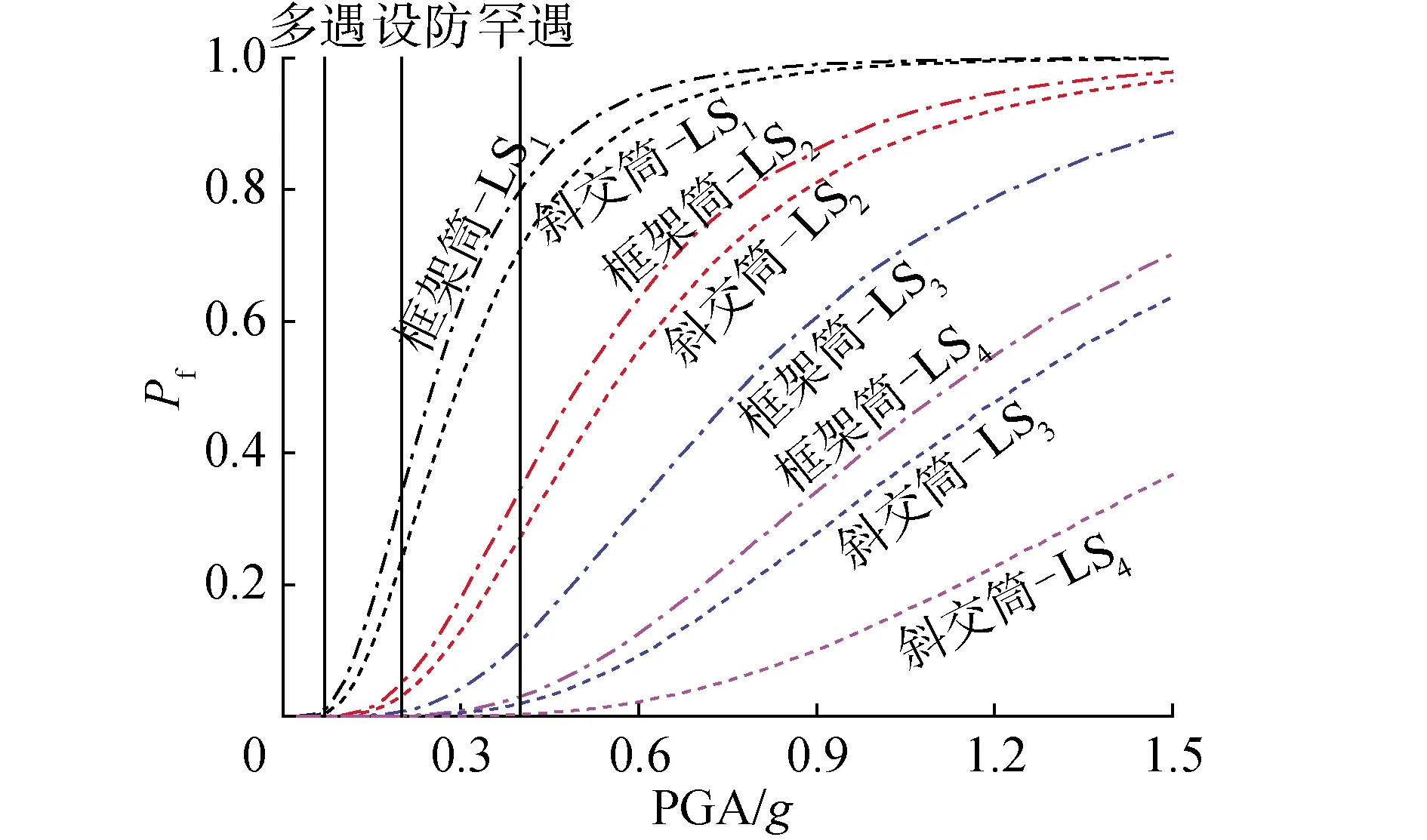
图7 易损性曲线

在本文结构所在地区规定下的8度多遇、设防和罕遇地震条件下的PGA分别为70、200和400 cm/s2，根据图7易损性曲线中各极限状态所对应的超越概率，可以得到相应结构在处于各性能状态时的概率分布情况，如表3所示。可以看出在遭遇相当于多遇地震作用下时，框架筒和斜交筒处于正常运行状态的概率分别是98.68%和99.41%，结构基本保持完好无损；在遭遇相当于设防地震下的作用时，2个结构仍有66.28%和76.42%的概率是可能处于正常运行状态的；在遭遇罕遇地震下的作用时，2个结构处于正常运行的概率分别为20.05%和29.12%，处于仅经简单修复后可继续立即使用的概率分别为45.49%和43.79%，而可能发生倒塌的概率分别仅为8.27%和1.92%。说明2个结构均能满足“小震不坏、中震可修、大震不倒”抗震性能需求，而且斜交结构更容易满足抗震性能的需求。

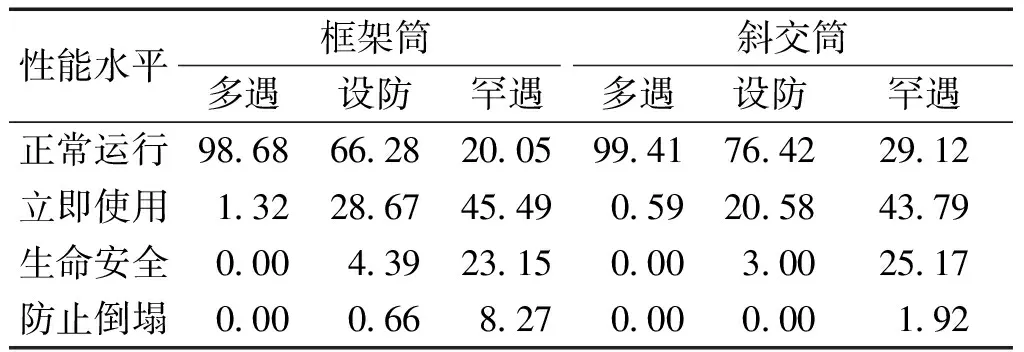
表3 各性能所处状态的概率

4 结论

1)框架筒结构的破坏过程以外筒腹部的底部各楼层柱脚和内筒连系梁的塑性铰开展为主，在结构倒塌之前主要由内筒的连系梁屈服耗散地震能量。斜交筒结构的破坏过程主要是外筒底部各层斜柱柱顶、柱脚以及内筒连系梁塑性铰的开展，结构的地震耗能过程主要靠外筒斜柱和内筒连系梁。

2)因框架筒和斜交筒两结构的侧移刚度有别。根据静力弹塑性分析先确定结构的性能水平极限状态的量化指标，再进行基于性能的易损性分析，更能体现结构的真实破坏状态和失效概率。分析结果显示：斜交筒结构相较于框架筒结构的抗震性能更优，特别是当结构遭遇超大地震作用时有更大的抗倒塌性能。本文中两筒中筒结构均能满足“小震不坏、中震可修、大震不倒”抗震性能需求，而且，斜交网格结构更容易满足抗震性能的需求。