雷达框架角约束下高空巡航导弹末制导策略

2021-07-13孙明玮周瑜朴敏楠陈增强陈志刚

哈尔滨工程大学学报 2021年7期

孙明玮，周瑜，朴敏楠，陈增强，陈志刚

(1.南开大学人工智能学院，天津 300350；2.中国运载火箭技术研究院空间物理重点实验室，北京 100076)

雷达导引头是导弹实现精确打击的重要子系统。雷达安装在导弹头部，导引头纵向框架角为目标视线角与俯仰姿态角之间的夹角。由于天线罩受到导弹气动外形、空间安装位置和机械结构的限制以及俯仰方向不对称的影响，某型高空巡航导弹雷达框架角位于一定范围时，天线罩的屏蔽作用将导致导引头不能正常工作，造成雷达工作盲区，对于最终打击精度造成很大影响。

传统的导弹雷达盲区问题都是针对命中目标前的最后时刻，由于弹目距离过近，造成雷达观测信息饱和的情形。这类问题，通用的解决办法是将控制舵卡死，使导弹按照惯性飞行。如张守钰等[1]研究了盲区期间舵处于中间位置和非中间位置对脱靶量的影响。高峰等[2]提出了一种导弹在末端盲区按舵偏角方案进行方案飞行的控制方法。针对高精度导引头的最小视场角约束问题，国内外学者开展了相关研究并取得一定成果[3-6]。但是从目前的文献报道而言，本文所研究的特殊制导过程中的雷达盲区问题还没有见诸过公开报道。

在落角约束的前提下，通过弹道分析，发现不同末制导距离对应的雷达盲区持续时间长短不同。根据系统性优化思想，本文提出了一种闭环目标估计-开环预测-闭环再修正的综合制导策略，以减小天线罩造成的盲区所导致的精度下降程度。数学仿真验证了算法的有效性。

1 导弹动力学与制导规律

1.1 导弹纵向动力学模型

导弹纵向动力学方程组[7]为：

(1)

式中：m为导弹质量；V是导弹速度；P为发动机推力；α为攻角；θ是弹道倾角；ϑ为导弹俯仰角；ωz是俯仰角速度；g为重力加速度；X为阻力；Y为升力；Jz为导弹俯仰转动惯量；Mz为俯仰力矩分量。

导弹所受空气动力和气动力矩计算公式为：

(2)

式中：S是特征面积；q=0.5ρV2为动压头；ρ为导弹所处高度空气密度；Lb为导弹参考长度；mz为气动力矩系数，cx、cy为气动力系数，这些系数均被表示成马赫数Ma，α和升降舵偏角δe函数，具体参见Winged-Cone模型[8]。Winged-Cone模型作为研究高超声速和超声速巡航飞行制导与控制的平台，目前被学术界普遍采用。

1.2 落角约束最优比例导引

导弹除了要命中目标以外，还要发挥出其最大毁伤效能和提高突防概率，因此导弹往往在纵向要以一定的姿态和弹道倾角命中目标[9]。目前最常用的落角约束最优比例导引规律为[10-11]：

(3)

图1 导引头模型

1.3 三回路过载驾驶仪设计

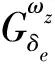
图2 三回路过载驾驶仪结构

2 目标状态估计

由于打击目标为地面或者海面低速移动目标，机动能力有限，可以假设其短时运动形态近似为匀速直线运动。为了估计目标的运动学信息(位置和速度)，需要建立弹目纵向平面惯性坐标系，如图3所示。其中ym是导弹飞行高度，xm是导弹的航程，xt是目标的横坐标。

需要注意的是，导弹在进入末制导之前一般经历了长时间的飞行，自身的惯性导航已经存在一定的累积速度和位置误差。由于对于目标信息的估计是基于弹目距离和视线角，因此，无法对于目标的绝对惯性位置和速度进行准确的估计，只能估计出把导弹视为惯性坐标系的目标相对位置和速度，而导弹的惯性误差已经包含在这些估计中。由于导弹的末制导时间很短，惯性器件此时间段内误差的进一步漂移可以忽略。可以假设目标的相对运动方程为：

xt=at+b

(4)

式中：a是目标相对运动速度；b是估计初始时刻目标的相对位置。根据图3中几何关系，可得r、q的表达式为：

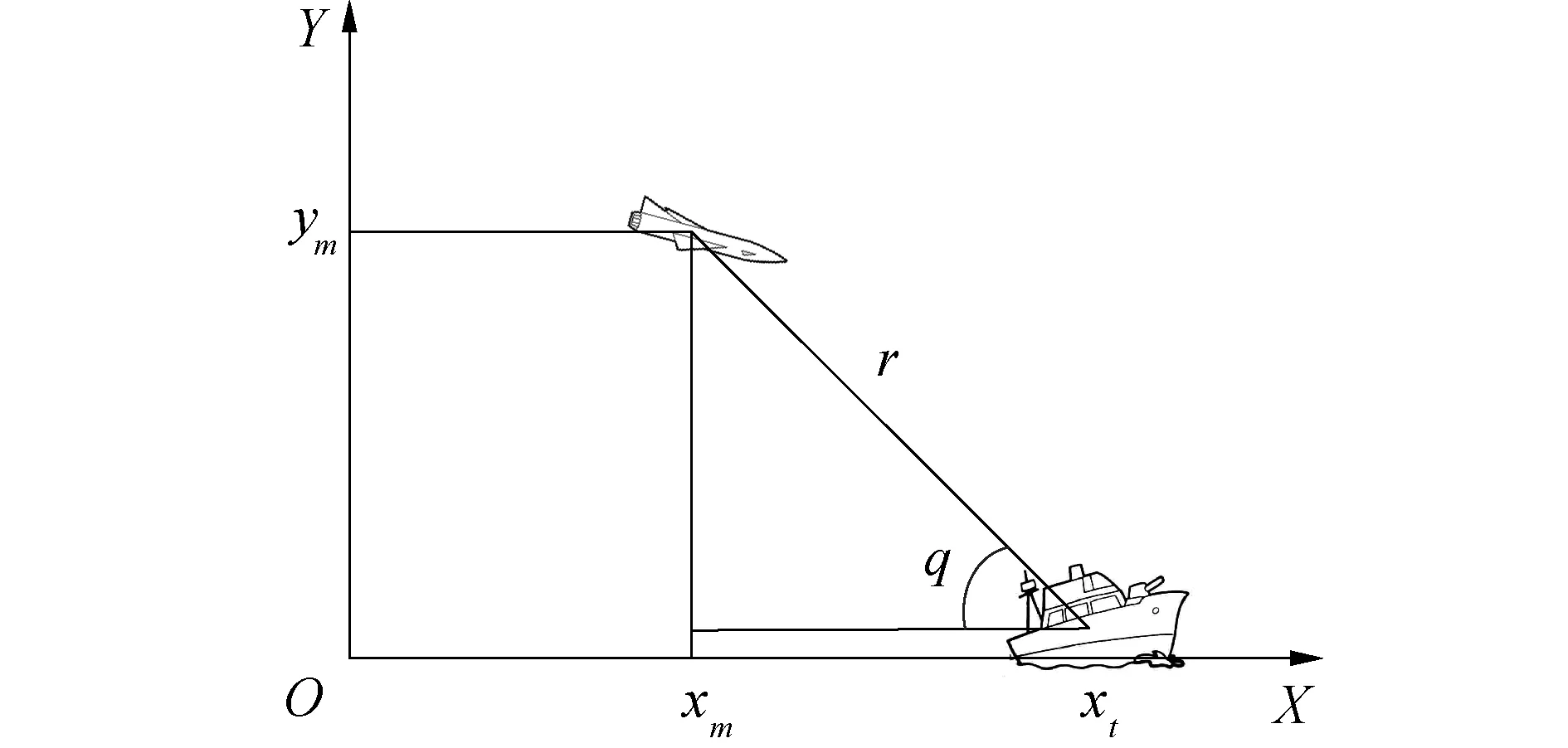
图3 导弹与目标几何关系

(5)

(6)

建立目标函数

(7)

单纯形搜索法是解决非线性最小二乘问题的实用方法[14]，使用单纯形法进行优化的流程如图4所示[15]。这里，λ是模型的参数点，表示对包含元素a与b的二维参数向量的一个估计，也是单纯形的顶点；n为待估计参数点个数；λi表示这组参数点中除对应目标值最大的参数点λM之外的其他点。根据单纯形的搜索算法，每次确定3个参数点，同时计算出λM和对应目标值最小的参数点λl，然后根据探索规则找到一个新的参数点λ*，用其取代λM，并对目标值进行计算和比较，根据算法流程，直到确定满足收敛条件的参数点。

图4 单纯形搜索法实现流程

3 数学仿真与对比分析

3.1 场景参数设置

数学仿真用到的导弹与目标的参数如下：初始高度30 km；初始速度6Ma；纵向参考长度24.384 m；参考面积334.73 m2；导引比例系数4；积分系数K1=0.025；俯仰角速度反馈系数K2=1；俯仰角反馈系数15；导引头白噪声均值0，标准差0.548 5；弹目距离测量误差±300 m；导弹速度零漂误差2 m/s；目标速度10 m/s；框架角盲区范围-5°～0°；落角约束设定值-70°。

3.2 最优制导距离的确定

本文中，将导弹高度为0时，导弹与目标的水平距离记为脱靶量。由于导弹存在落角约束，使得盲区时间长短与制导距离有密切关系。为了确定最佳制导距离，先在理想条件下，即不考虑弹目距离测量误差、导引头白噪声和雷达盲区的存在，从42 km到47 km，每隔1 km选取不同的制导距离进行仿真，研究框架角、视线角、弹道和速度随时间变化的规律。仿真结果如图5～9所示。

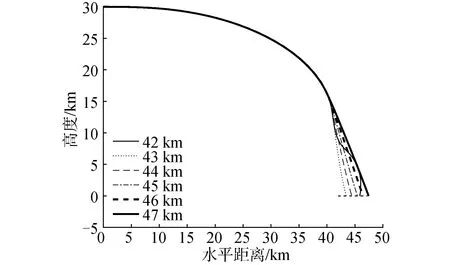
图5 不同制导距离对应的高度

由图5可以看出，当制导距离为42 km时导弹没有稳定的直线弹道，最后脱靶量严重；制导距离越大，弹道在末期越平直。由图6和图7可以看出，当制导距离为42 km时，框架角不收敛到0；随着制导距离增大，框架角最后收敛到零。当制导距离在43～45 km时，相较于其他制导距离，盲区时间短，同时导弹在脱离盲区后命中目标前雷达导引头有效工作时间长。由图8可以看出，当制导距离大于42 km后视线角可以收敛到-70°，满足落角约束要求。特别需要指出的是，当制导距离在43 km到44 km时，视线角先降低到接近-80°，后又回升到-70°，正是这段时间，视线角经过调整最后达到-70°，使导引头在跨出盲区后有效工作时间加长。图9显示了不同制导距离下马赫数随时间变化的情况。盲区时间与脱靶量统计具体仿真结果如表1所示。

图6 42 km制导距离下的框架角

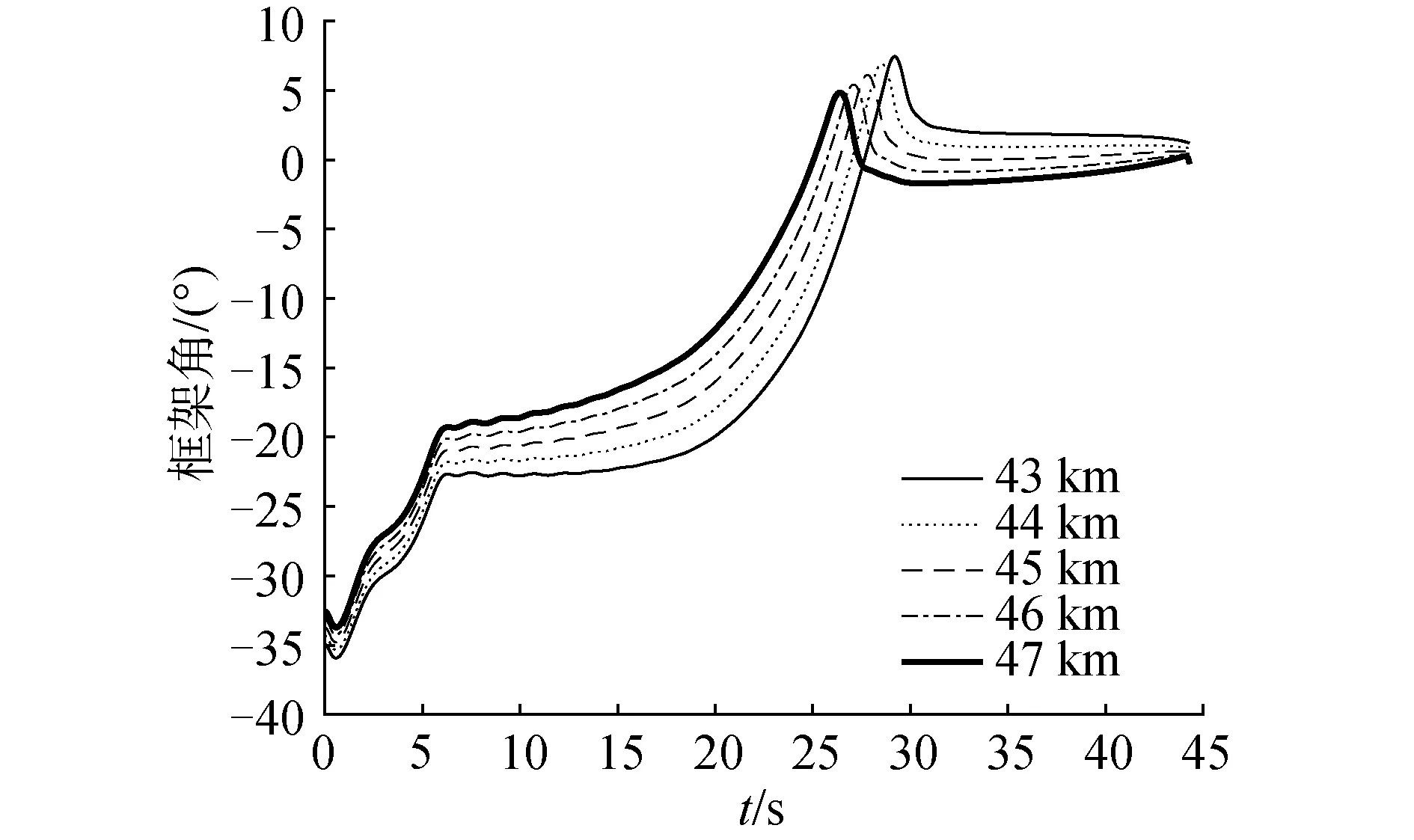
图7 不同制导距离对应的框架角

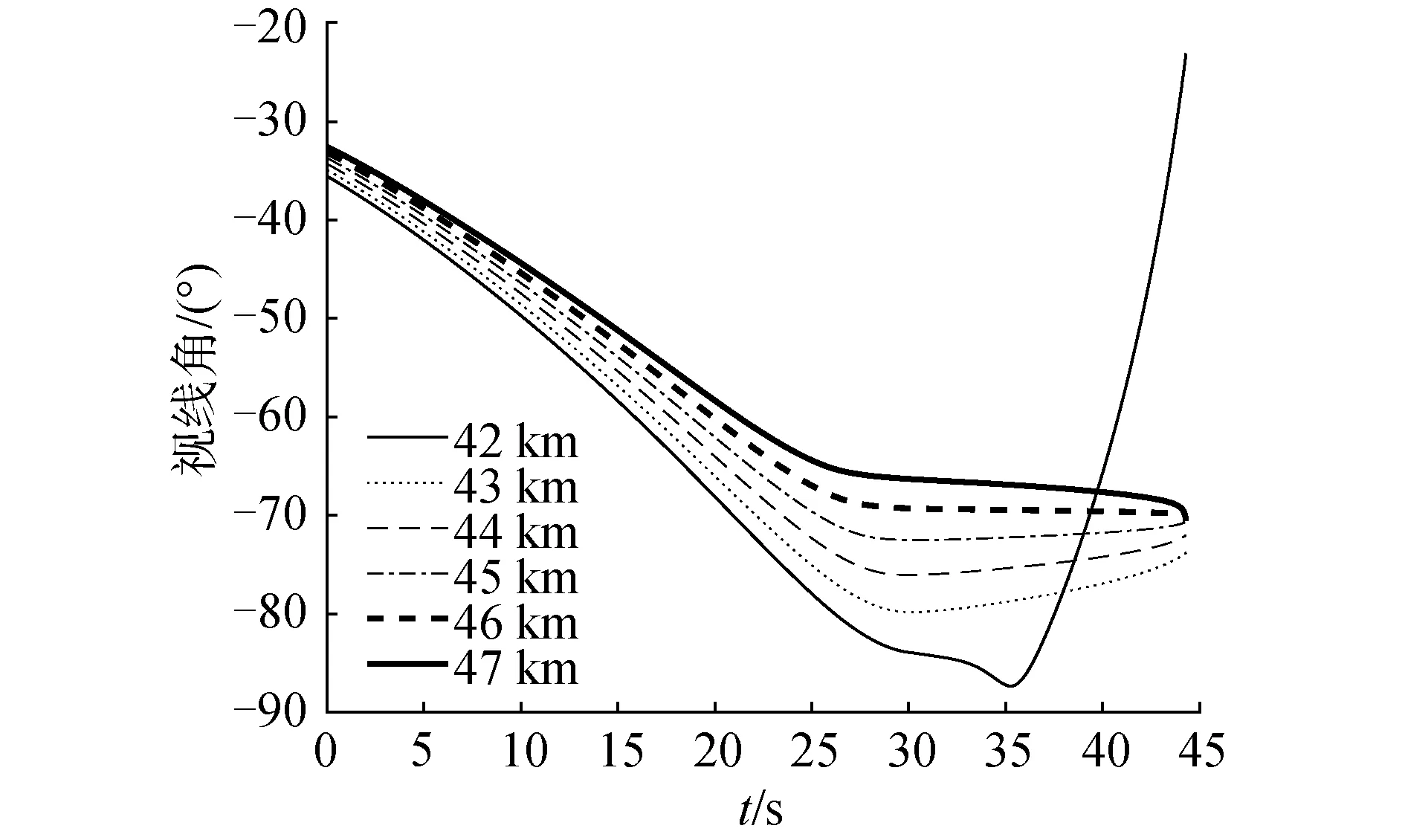
图8 不同制导距离对应的视线角

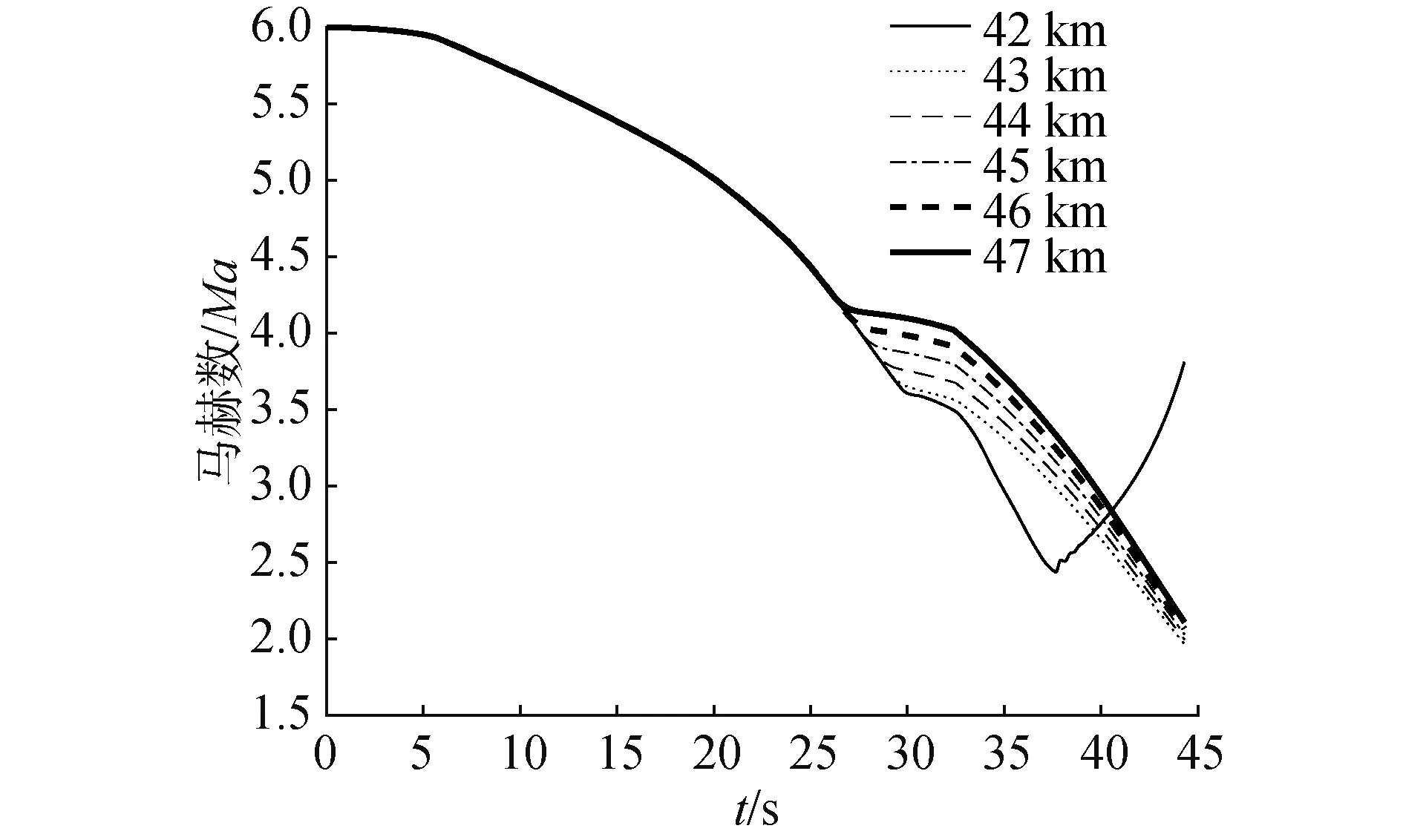
图9 不同制导距离对应的马赫数

表1 不同制导距离下脱靶量、时间的统计

根据表1可见，当制导距离为42 km时，脱靶量非常大。当制导距离超过43 km时导弹可以命中目标。在满足脱靶量要求情况下，制导距离为43 km～45 km时，盲区时间短并且之后导引头有效工作时间长。制导距离继续增加，盲区时间明显变长，导引头有效工作时间变短，脱靶量有所提高，为了提高制导精度，需要缩短盲区时间延长后续导引头有效工作时间。综合考虑，选择44 km作为最佳的制导距离，这样对于不确定性也保留了适当的裕度。导弹阻力系数和升力系数在标称值±10%摄动范围内且满足脱靶量小于10 m的条件下，最佳制导距离对应落地速度的波动范围在1.5Ma～2.3Ma。

3.3 仿真对比与分析

此类制导过程中特殊的雷达盲区问题尚未见诸过公开报道，因此可供对比的制导策略有限。为验证综合制导策略的可行性及优越性，根据导弹离开盲区之后是否继续使用目标的估测信息设计2种制导控制方案进行对比。第一种为开环制导，是指在导弹进入盲区之后(包括跨出盲区时间)，全部使用目标的估计位置形成的制导信息对导弹进行导引；另一种为本文提出的综合制导策略，雷达盲区内使用目标位置估测信息，离开雷达盲区后使用实际测量的目标位置信息。

通过单纯形搜索算法辨识出目标运动速度a，初始位置b。单纯形搜索法的参数选择如下：单纯形边长170；反射系数rr=1.3；收缩系数rc=0.45；开拓系数re=2.1；停止条件ε=0.000 1。

2种制导方案脱靶量仿真结果的统计显示，在进入盲区之后的所有时间里全部使用目标估计位置形成的制导信息对导弹进行导引，脱靶量的圆概率误差为57.20 m，而综合制导策略下脱靶量分布明显小于开环制导，圆概率误差为21.02 m。这得益于在制导末期，导引头的框架角大于零度，导弹可以根据实际测量出的目标位置信息进行导引，此时脱靶量的大小主要与导引头的测量噪声有关。在不考虑盲区的前提下，仅由噪声所造成的脱靶量的圆概率误差为10.72 m。