基于Mathematica 的牛顿环干涉与折射率关系的讨论*

张丽颖，顾菊观

(湖州师范学院理学院，浙江 湖州 313000)

1 引言

当光从光疏介质近似垂直或掠入射到光密介质时，反射光有位相突变（或称半波损失）。薄膜干涉中，当薄膜处于介质中，其上下表面反射时，两束反射光之间因位相突变必然会产生额外的位相差或光程差。对于牛顿环干涉，上下表面及干涉膜折射率大小关系不同时，其对应的额外光程差不同。目前的光学教科书，对于额外光程差给出的表达式大致分为三类，姚启均《光学教程》中额外光程差取/2-λ[1]；章志鸣《光学》教材中额外光程差取 2/λ[2]；钟锡华《现代光学基础》中额外光程差表述则取0 即不考虑半波损失因素[3]，可见上述教材对于额外光程差都没有给出一个明确的定义。郭有能[4]等人也曾在研究牛顿环干涉的过程中讨论了不同折射关系下的额外光程差，但其分析结果依旧不够准确。显然这对初学者理解半波损失和额外光程差造成了一定的困难。

另外，通过计算机软件可以模拟出各种情况下的干涉仿真图像，其结果对于分析能够起到一个很好的参考作用。唐平英[5]等人在研究光的衍射时就利用Mathematica 中交互功能更加生动形象地向读者展示了模拟图像。关于牛顿环干涉实验，目前已有许多利用Matlab 模拟得出的研究成果。例如，郭天宇、韦仙、申惠娟[6-8]等学者研究的入射光波长、曲率半径、折射率等因素对于牛顿环干涉图案变化的影响，但仿真图样基本为静态图且不够生动形象。

基于上述两个问题，将在已有的基础上进一步探究当牛顿环上下表面及干涉膜的折射率大小关系不同时，其对应的光程差的表达式。并借助Mathematica 软件模拟出的光强分布和条纹干涉图样对其进行具体分析。根据曹佳妍[9]等人的研究可知牛顿环干涉图样的改变会影响牛顿环半径的测量，因此该研究结果不仅能够更加形象直观地加深学生对光干涉现象的理解，了解和掌握Mathematica 在物理学及光学中的应用，而且对于教学工作也具有很好的指导意义。

2 牛顿环干涉原理

如图1 牛顿环结构图所示，上面部分为平凸透镜，下面部分为平面玻璃，中间部分则是平凸透镜的凸球面和玻璃平板之间形成的簿膜。当平行单色光垂直入射于平凸透镜的平表面时，薄膜的上下两表面（平凸透镜的下表面和平板玻璃的上表面）所引起的反射光线产生干涉，因相同光程差即相同厚度处对应的轨迹是圆，因此使干涉图样呈圆环状，即牛顿环。

图1 牛顿环结构图

设介质薄膜上下两表面反射光的光程差为δ，当δ=jλ时，干涉加强，形成亮条纹；当

时，干涉减弱，形成暗条纹；根据几何关系，

由于R＞＞d，d2可以略去，则

由于两列相干光的光强很接近，因此可以近似认为I1=I2=I0,则两列光波在干涉场中相遇时的光强为

3 折射率对光程差影响

由于n1、n2、n3三者关系的不同，需要考虑半波损失。半波损失是指当入射光在光疏介质中前进，遇到光密介质的界面时，在掠射或正入射两种情况下，反射光的振动方向对于入射光的振动方向都几乎相反，即产生半波损失[1]。

对于多束光线（如图2所示）的干涉问题，鲁一清[10]等人已进行了具体的讨论，结果表明只有1、2两光束会发生干涉。接下来，对于1、2两束光的光程差本文将根据折射率n1、n2、n3的大小关系分为三类情况具体讨论。

图2 光束干涉示意图

3.1 n1 ＜ n2＞n3时的光程差

根据半波损失产生条件，可知薄膜上表面反射光1产生半波损失(L1=L10+λ/2)，薄膜下表面产生的反射光2无半波损失(L2=L20)，结果两束反射光有额外位相差π，即额外光程差为λ/ 2，则光程差：

3.2 n1 ＞ n2＜n3时的光程差

根据半波损失产生条件，可知薄膜上表面反射光1无半波损失(L1=L10)，薄膜下表面产生的反射光2产生半波损失(L2=L20+λ/2)，结果两束反射光有额外位相差π，即额外光程差λ/ 2，则光程差：

3.3 n1＞ n2＞n3和 n1 ＜ n2＜n3时的光程差

根据半波损失产生条件，n1＞n2＞n3情况下1、2两束反射光均无半波损失(L1=L10，L2=L20)；而n1＜n2＜n3情况下1、2两束反射光均产生半波损失（L1=L10+λ/2，L2=L20+λ/2）。两种情况下的1、2两束反射光额外位相差都为0，即额外光程差为0，则光程差：

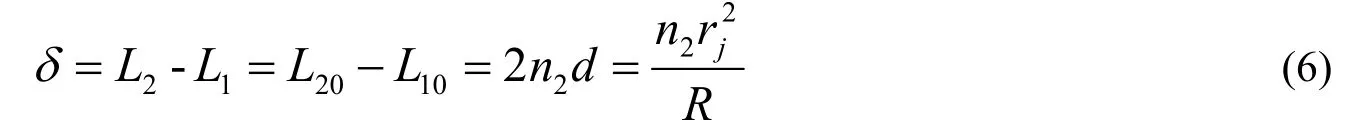
4 折射率对光强分布和干涉图样的影响

在Mathematica 仿真过程中，利用‘Manipulate’命令将交互式动态光强分布与条纹干涉图样呈现出来.通过改变薄膜的折射率n2得到以下动态仿真图像：

4.1 n1 ＜ n2＞n3时的光强分布和干涉图样

已知Δφ=，结合(3)、(4)式得到合成光强

令n1=n3=1.5、R=1.5m、λ= 550nm，改变折射率n2，可得：

从图3 可分析知，在n1＜n2＞n3的情况下，牛顿环中心光强为极小值且干涉条纹中心为暗纹。当折射率n2增大时，条纹整体向中心缩小但不消失，相邻的最大或最小的光强对应的间距逐渐变小；而对于干涉图样来说，条纹数量逐渐增多即明暗条纹间距越来越密。

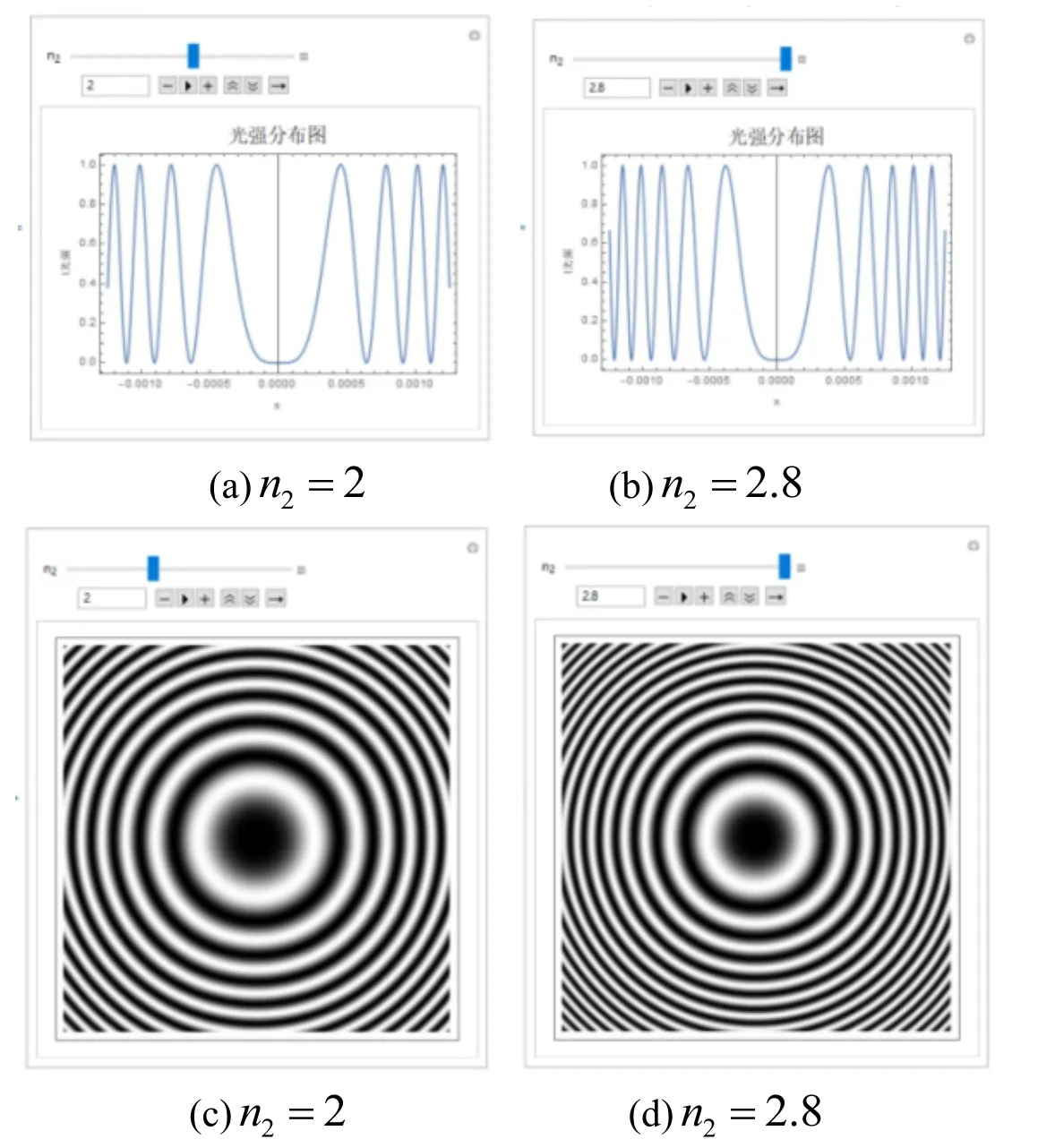
图3 n1 ＜ n2＞n3时折射率 n2改变的光强分布与干涉图样

4.2 n1 ＞ n2＜n3时的光强分布和干涉图样

已知Δφ=，结合(3)、(6)式得到合成光强

令n1=n3=1.6、R=1.5m、λ= 550nm，改变折射率n2，可得：

从图4 可分析知，在n1＞n2＜n3的情况下，牛顿环中心光强为极小值且条纹中心为暗纹。当折射率n2增大时，条纹整体向中心缩小但不消失，相邻的最大或最小的光强对应的间距逐渐变小；而对于干涉图样来说，条纹数量逐渐增多即明暗条纹间距越来越密。

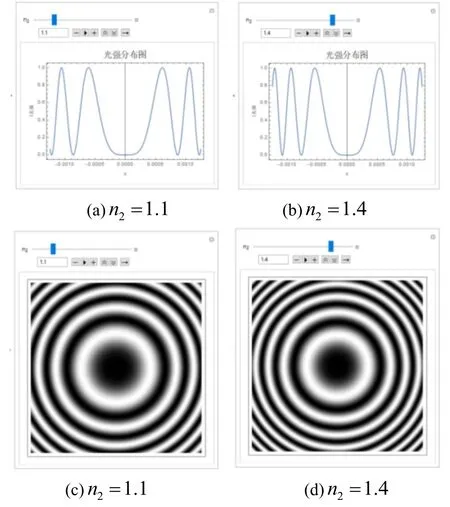
图4 n1 ＞ n2＜n3时折射率 n2改变的光强分布与干涉图样

4.3 n1＞ n2＞n3和 n1 ＜ n2＜n3时的光强分布和干涉图样

已知Δφ=，结合(3)、(8)式得到合成光强

当折射率关系为n1＞n2＞n3时，令n1=2.8、n3=1.35、R=1.5m、λ= 550nm；当折射率关系为n1＜n2＜n3时，令n1=1.35、n3=2.8、R=1.5m、λ= 550nm，两种情况下改变折射率n2得到的图像一致。

从图5 可分析知，当折射率n2增大时，条纹整体向中心缩小但不消失，相邻的最大或最小的光强对应的间距逐渐变小且明暗条纹间距越来越密。对比图3、4，可发现在折射率大小关系为n1＞n2＞n3和n1＜n2＜n3时，牛顿环中心光强为极大值，即干涉图样中央条纹为亮纹。

图5 n1＞ n2＞n3和 n1 ＜ n2＜n3时折射率 n2改变的光强分布与干涉图样

4.4 小结

在折射率n1、n2、n3大小关系不同的情况下，其干涉条纹图样的变化趋势一致：随着薄膜折射率n2的增大同一干涉级条纹由外向中心移动，所能看到的条纹数量逐渐增加，由此得出条纹半径rj和相邻条纹间距Δr会随着薄膜折射率n2的增加而减小。不同的是，对于n1＜n2＞n3和n1＞n2＜n3两种情况，在折射率n2相同时其条纹数量、明暗条纹分布完全相同且圆环中心为暗纹。而对比图5，可发现在折射率大小关系为n1＞n2＞n3和n1＜n2＜n3时，在折射率n2相同的情况下，干涉图样条纹数量增多，同一级的干涉条纹半径变小且圆环中心为明纹。

5 总结

根据半波损失原理讨论了在牛顿环上下表面及干涉膜的折射率大小关系不同时对应的额外光程差，并利用Mathematica 软件对牛顿环的光强分布和干涉现象进行了动态的仿真模拟。仿真过程中通过调整输入参数，模拟出不同折射率情况下牛顿环干涉实验的光强分布情况，生成的动态条纹干涉图样也更直观地显示出了随着参数的改变牛顿环疏密、明暗程度的变化。有利于加深学生对于牛顿环干涉知识点、半波损失和额外光程差的理解。因此，计算机模拟生成的仿真图样可以广泛用于实验及理论教学过程中，不仅能够有效地弥补实验教学中的局限，而且为学生进一步的探索与深入学习理论知识提供了不可缺少的途径。