关门时车内声场的仿真与试验研究*

刘 哲，高云凯，徐 翔，陈佳举，马 超

（同济大学汽车学院，上海 201804）

前言

车门作为汽车开闭件的重要组成部分，其关闭时所产生的振动噪声在开闭件中占主导地位［1-3］。消费者在购买汽车时，首先接触到NVH问题便是车门关闭所产生的，因此这将直接影响到消费者的购买意愿。关门工况下的车内噪声测试均是在整车制造完成后才能通过试验测试获得。因此在已制造出首批车辆的情况下，如何对后续批次车辆的车内噪声进行改进预测显得尤为重要，这对后续车门的结构改进优化有着重要的指导意义［4-7］。

近些年来，国内外许多学者对车内噪声和关门声品质问题进行了研究。史文库等［8］对某型号纯电动客车在加速和匀速工况下的振动噪声进行了研究，总结出了振动噪声特性，为下一步的优化改进提供了依据。陈昌明等［9］利用多体动力学、有限元法和边界元法分析了路面不平激励对车内低频噪声的影响。代文强等［10］采用能量有限元分析方法对高速列车车内的噪声进行了预测研究，结果发现仿真数据和测试结果在分析频带内的声压级一致性较好。王登峰等［11］利用统计能量分析法对来自动力总成振动和路面随机激励在车内产生的噪声进行了预测研究，通过试验验证了该方法的可行性。唐中华等［12］利用虚拟传递路径分析方法对车内低频振动噪声进行了分析，并根据结果对其进行了优化。Fiedler等［13］利用统计能量分析法预测了轻轨车辆的内部声压级，并对各种噪声贡献路径进行了研究。Kim等［14］提出了利用混合传递路径分析方法预测动力总成振动引起车内噪声的方法。Zhang等［15］利用有限元和边界元方法分析了车门关闭声品质，并对车门主要设计变量进行了灵敏度分析。杨川等［16］提出了一种基于经验模态分解与反向传播神经网络相结合的汽车关门声品质预测方法并验证了该方法的预测精度。Champ等［17］通过对环形圆盘进行振动噪声的数值仿真，验证了对车门关闭声品质进行数值仿真的复杂性。Kumar等［18］研究了通过改变车门的设计因素来改善关门声品质的可行性。杨川等［19］针对汽车关门噪声进行了优化分析，采用响应面法，以关门动能最小为目标，以车门主要板件厚度为设计变量，建立了一套优化流程并验证了该方法的有效性。

上述对车内噪声的研究主要聚焦激励源为动力总成或路面激励，对关门声品质的研究方法局限于数值仿真分析，均未应用到车门关闭工况下车内噪声的预测研究。因此本文中以某车型为研究对象，利用实验和仿真相结合的方法对其关门工况下车内噪声进行预测分析。本文中对车门关闭时的瞬态载荷进行离散化设计，利用传递路径分析（TPA）方法求取离散化的瞬态载荷，将其作为瞬态有限元模型的输入量，进而将其瞬态振动响应映射至声腔边界元模型，最终得到驾驶员耳旁声压。对车门关闭工况下车内噪声进行预测研究取得了一致性较好的结果。因此，本文中验证了通过离散化车门关闭的瞬态载荷对预测车内声场的可行性，并为后续批次车门的设计提供了重要指导。

1 TPA基本理论

在时域TPA理论中，对线性时不变系统，目标点响应由结构声和空气声线性叠加得到［6］:

式中:Pl（t）为第l个目标点的总贡献量响应；t为时域数据；Pli（t）为第i条路径的结构载荷对目标点l的贡献量；Plj（t）为第j条路径的空气载荷对目标点l的贡献量；n和m分别为结构载荷和声学载荷的传递路径数量。

系统中每一个目标点响应由作用在该激励点上的激励载荷乘以该条路径的单位脉冲响应函数的卷积得到，则式（1）可写为

式中:fli（τ）和qlj（τ）分别为第i条路径的结构载荷和第j条路径的声学载荷；hli（t-τ）为第i条路径的结构载荷到第l个目标点的单位脉冲响应；hlj（t-τ）为第j条路径的声学载荷到第l个目标点的单位脉冲响应。

结构载荷和声学载荷对目标点响应的计算过程类似，为了文章的简洁性，本文中以结构响应为例进行分析。在机械系统激励点附近设置2倍的参考点用于求解激励载荷，得到参考点的响应和激励点至参考点的单位脉冲响应函数，利用逆矩阵法得到激励点载荷［2］。

式中:I（t）为参考点的振动响应；f（τ）为激励点激励载荷构成的n行列向量；h（t-τ）为各激励点载荷至参考点振动响应的单位脉冲响应函数。

利用反卷积即可从式（3）中求取激励点载荷f（t）。假设反卷积的单位脉冲响应函数为r（τ′），则参考点加速度响应I（t）通过反卷积系统时为

显然式（4）成立的前提是式（5）成立:

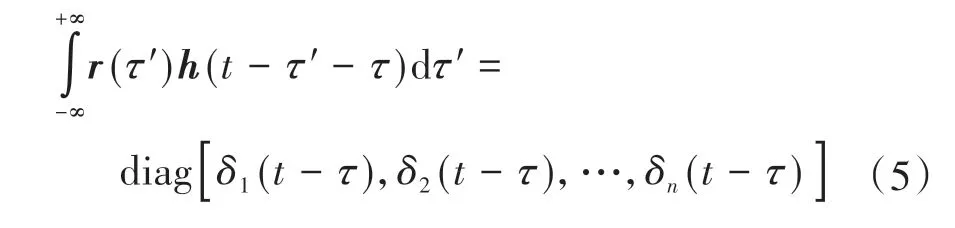
式中δ1（t-τ），δ2（t-τ），...，δn（t-τ）为δ函数。对式（5）做傅里叶变换得到:

式中:R（ω）和H（ω）分别为r（t）和h（t）的傅里叶变换；E为单位矩阵。

由式（6）可得R（ω）和H（ω）互为逆矩阵，因此首先测量得到各激励点至参考点的频响函数矩阵H（ω），通过求其逆矩阵得到反卷积系统的频响函数矩阵R（ω），利用频率采样法将其构造成有限脉冲响应数字滤波器矩阵，将参考点时域振动响应通过滤波便可得到激励点处的时域载荷。同样可以获得激励点至目标点的滤波器。

最终得到激励载荷的表达式为

式中:rn2n（t）为激励载荷fn（t）对参考点响应I（t）的单位脉冲响应函数；“⊗”表示卷积计算。

由于一般时域信号较长，应用基于分段准线性原理的离散形式对其进行离散。这种离散形式将时域信号分解为足够小的时间步长，然后对每一个步长进行卷积计算。离散形式的方程为

式中xl（tj）为第l个目标点在第j个时间步长的响应。

将式（7）代入式（8）中，可得到离散时域的响应结果。将每个时间步长依次排序，代入式（9）便可得到完整的时域响应结果。

2 分析流程

本文中分析流程如下:

（1）根据第1节中公式可知，在整车试验中测量参考点的加速度振动响应；

（2）在台架试验中测量激励点至参考点的频率响应函数；

（3）利用第1节中公式求出激励点的瞬态冲击载荷；

以Td1为界限,Td0～Td1段的斜率k1要小于Td1～Tdmax段的斜率k2,则有折线形特性曲线的数学表达式为

（4）建立整车模型，简化模型形成封闭声腔，建立车内声腔和座椅有限元模型，建立车内声腔和座椅边界元模型，建模流程如图1所示；

图1 模型建立流程

（5）将瞬态冲击载荷作用到车门有限元模型上求出瞬态加速度振动响应；

（6）进一步将瞬态加速度振动响应映射至声腔边界元模型从而得到声场处的声压值；

（7）最后将仿真数据与试验结果进行对比，确定该方法的可行性。

3 数据采集

本文中研究对象为某乘用车左前车门玻璃下位工况，开启方式为顺开式车门，关门速度为1.5 m/s。车门在关闭瞬时主要受到锁机（A1）和密封条（A2～A9）处的冲击载荷，因此对密封条处的冲击载荷进行合理的离散化处理成为建立车门TPA模型的重点。为了便于后续分析研究，将密封条处的冲击载荷离散为8个集中载荷［14］，离散化后的冲击载荷所在位置如图2所示。利用传递路径求取激励点载荷时，需要设置参考点，且参考点的数量为激励点的2倍或以上，参考点所在的位置如图3所示。通过前期的振动水平摸底试验可知，引起关门异常振动是有下位玻璃的异常振动所导致的［1-2］。由于密封条（A2～A9）处的冲击载荷仅为Y向，锁机（A1）处的冲击载荷为XYZ3向，因此离散化后的瞬态冲击载荷的自由度为3×1+1×8=11。参考点的自由度为3×16=48，因此满足TPA分析中参考点自由度为激励点自由度的2倍或以上的要求。

图2 离散化后的冲击载荷所在位置

图3 冲击载荷对应的参考点

3.1 整车试验

在图3所示参考点位置粘贴三向加速度传感器，如图4所示。三向加速度传感器的型号为PCB 35A16，信号采集系统为LMS公司的120通道数采系统，型号为LMSSC316⁃UTP，如图5所示。

图4 整车试验

图5 数采系统

由于不同操作者的差异会导致不同的关门速度，进而参考点处的振动响应和驾驶员耳旁声压响应也会不一致，因此如何确定统一的关门速度成为后续研究的关键。

在车身侧安装门速仪用于记录车门在关闭时的瞬时速度，利用弹性绳控制车门在关闭瞬时的速度，弹性绳的一端固连在车门内侧，弹性绳的另一端固连在车身内侧。弹性绳在弹性范围内，其产生的弹力与伸长量成正比，因此可以通过改变车门的旋转角度控制弹性绳产生的弹力进一步控制车门关闭时的瞬时速度。因此可以通过弹性绳和门速仪的互相配合完成常用关门速度的采集，本文中选取的常用关门速度为1.5 m/s，如图6所示。

图6 车门速度控制装置

由于车内噪声与测量位置有着直接关系，因此测点位置应该能够代表驾驶员耳旁的噪声分布，根据GB/T 18697—2002《声学汽车车内噪声测量方法》，在驾驶员耳旁布置传声器采集车内声压响应，传声器型号为MPA 201，如图7所示。

图7 车门速度控制装置

传感器的布置位置和数量如表1所示。

表1 传感器位置和数量

3.2 台架试验

由第1节可知，需要测量激励点至参考点的频率响应函数。利用力锤在图2所示激励点位置进行敲击。同理，在图3所示参考点位置粘贴三向加速度传感器拾取加速度振动响应，如图8所示。每次敲击5次取平均值作为最终的频率响应函数。

图8 台架试验

4 仿真分析

4.1 车门有限元仿真

车门系统有限元模型中，钣金件采用Pshell 2D面网格，铰链采用Psolid 3D四面体网格；车门内板和外板为包边处理采用共节点单元；车门外板和防撞梁为胶粘处理采用Area（adhesives）单元；车门内板与加强板为点焊处理采用Acm（equivalenced-（T1+T2）/2）单元；铰链和内板为转动轴连接采用Cbeam 1D单元。车门在关闭瞬时受到铰链处6个自由度的约束，为了保证有限元仿真与试验过程的一致性，在车门上下两个铰链处施加6个自由度的约束。车门有限元模型及边界条件如图9所示。

图9 冲击载荷的作用点

根据3.1节整车试验和3.2节台架试验，采集的参考点加速度振动响应和激励点至参考点的频率响应函数，利用第1节中公式求出激励点处（见图2）的瞬态冲击载荷，如图10所示，可以看出车门关闭时受到的载荷为作用时间极短的瞬态冲击载荷，符合车门关闭工况的受力情况。将求出的瞬态冲击载荷作用到激励点处（见图9），求解车门有限元模型的瞬态振动响应。

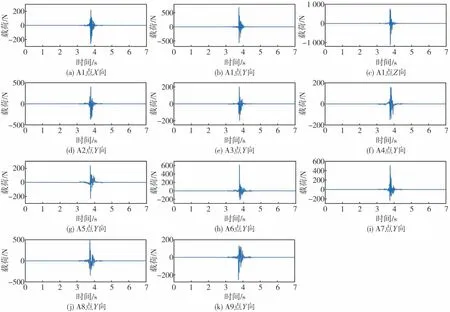
图10 激励载荷

图11为车门关闭瞬时的加速度振动响应云图，可知车门门框处的加速度振动响应幅值最大，与试验测试结果一致。

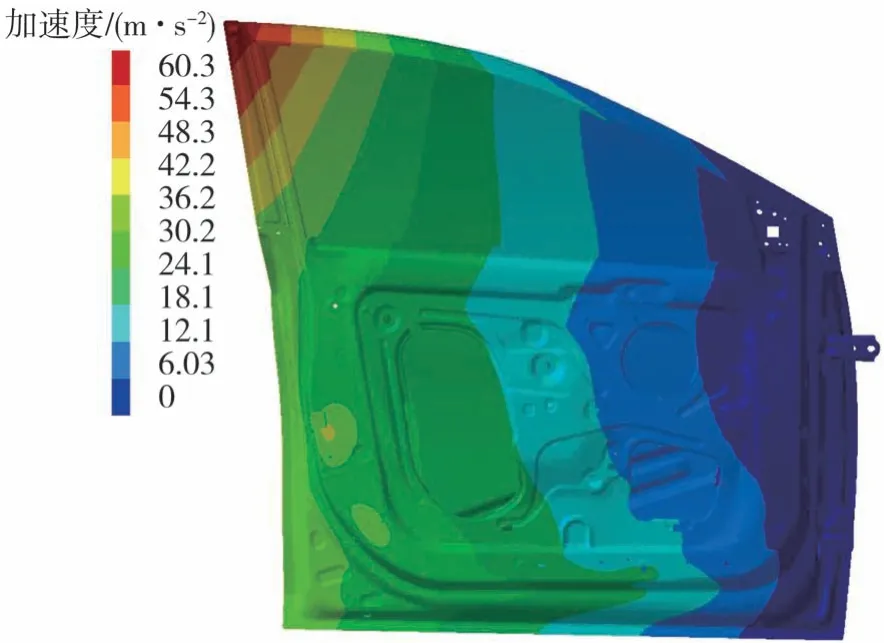
图11 车门振动响应云图

4.2 时域边界元仿真

装饰车身有限元模型包括白车身和相应零部件，共计2 489 087个单元，如图12（a）所示。进行车内驾驶员耳旁声场预测分析前需要对乘客舱空腔和座椅有限元建模，因此需要对车身进行模型质量修复并简化，填充车身的特征孔洞以形成封闭空腔，如图12（b）所示。对乘客舱空腔和座椅空腔进行有限元建模，通过布尔运算使其分离，单元大小为50 mm，均为CTETRA四面体单元，共计884 939个单元，如图12（c）所示。在乘客舱和座椅有限元的表面进行提取面网格、粗化表面等操作，得到共计7 526个单元，如图12（d）所示。

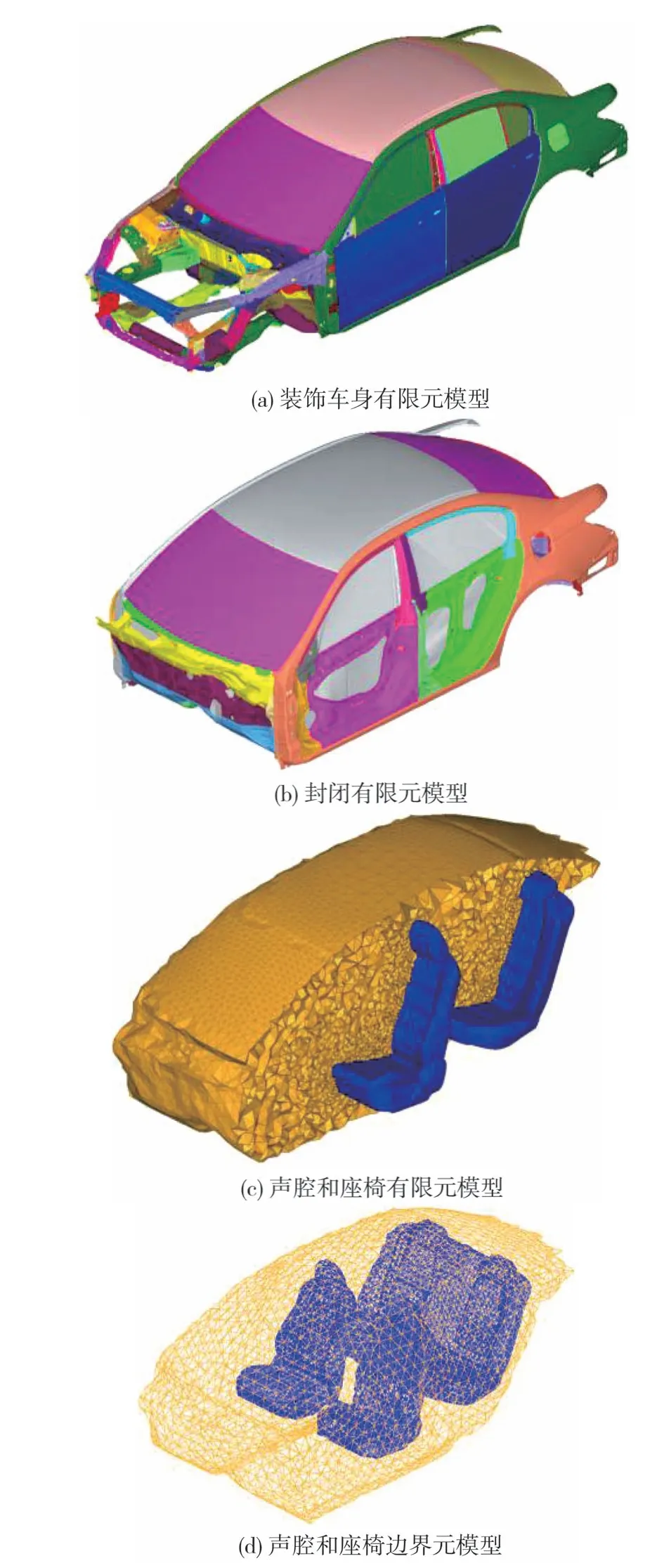
图12 边界元建立流程

本文中选择时域边界元法计算车内声场，时域边界元需要的网格为三角形面网格，因此声腔和座椅边界元模型为三角形面网格，场点模型为四边形面网格，如图13所示。定义流体为空气，声速为340 m/s，密度为1.225 kg/m3。通过声阻抗定义材料的吸声属性，座椅的声阻抗为975 Pa∙s∙m-1，内饰的的声阻抗为830 Pa∙s∙m-1。

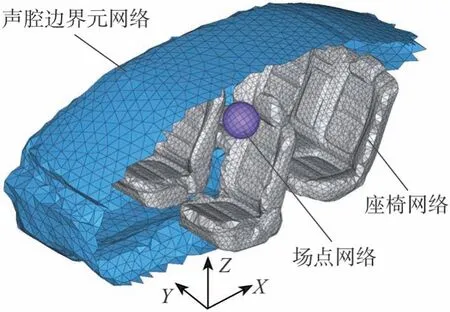
图13 边界元模型

时域边界元法是将结构有限元的加速度振动响应结果通过插值方法映射到声学边界元网格上，进而进行辐射噪声计算。图14为场点网格处的声压云图响应。进一步提取驾驶员右耳坐标位置处的声压响应，并将其转化为声压曲线，如图15所示。

图14 场点处声压响应

由图15可知，试验结果和仿真数据在整体趋势和局部峰值的一致性较好，仿真数据捕捉到了车门关闭工况下驾驶员耳旁的短时瞬态声压响应。

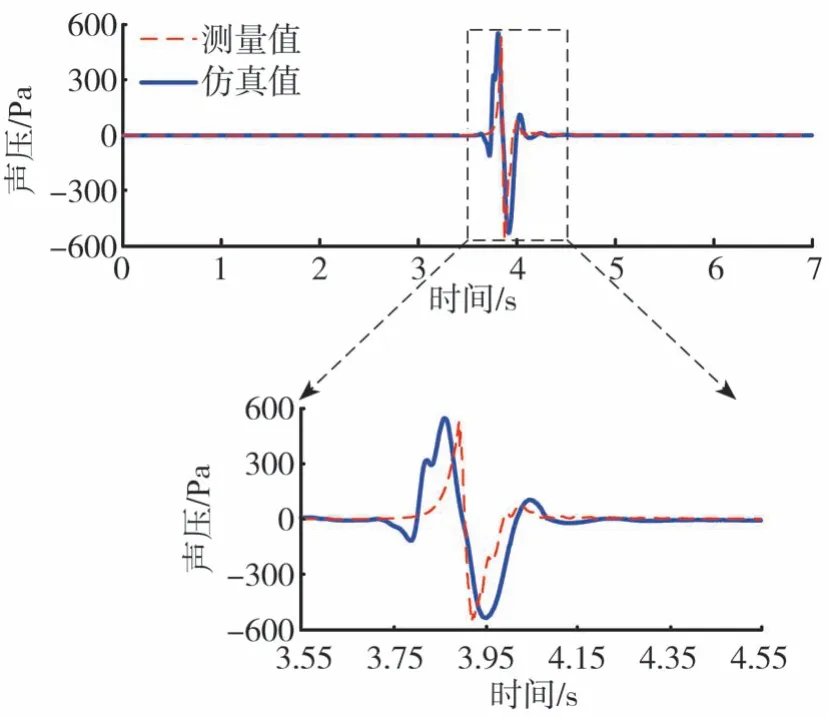
图15 耳旁声压实测值与仿真值

为了进一步比较目标点的实测值和仿真值的吻合程度，本文中采用均方根误差（RMSE）作为比较准则进行误差分析，其公式［20］为

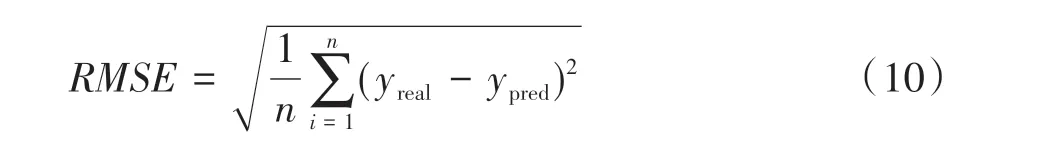
式中:yreal为实测数据；ypred为仿真数据。

RMSE值越小，表明仿真数据ypred和实测数据yreal的误差越小。驾驶员右耳处的实测声压响应和仿真声压响应的RMSE值为0.749，说明两者在趋势上重合度较好，因此本文中提出的声固耦合分析方法和离散化传递路径分析模型适用于关门工况下车内声压的预测分析。

5 结论

针对乘用车关门工况下车内声场预测仅能在整车制造完成后才能测量的问题，本文中通过设计整车和台架试验，对车门关闭载荷进行离散化设计，利用TPA方法计算出离散载荷并施加到车门有限元模型，求得车门瞬态振动响应，将加速度振动响应结果映射至声腔边界元，最终得到驾驶员耳旁声压响应，并比较了仿真数据与实测结果，得到了具有良好的一致性的结果，本文中所做的工作和得到的主要结论如下。

（1）对车门关闭工况下的冲击载荷进行了离散化研究，利用TPA方法求出了车门关闭时的瞬态冲击载荷，求出的载荷符合车门关闭工况下短时瞬态冲击的性质，验证了TPA方法在求取关门冲击载荷时的可行性。

（2）对车门进行了有限元建模、对声腔进行了边界元建模，针对车门关闭工况，进行了瞬态振动有限元分析和时域边界元的声固耦合联合仿真，得到了驾驶员耳旁声压，验证了该方法在求取关门工况下驾驶员耳旁声压的可行性。

（3）分析结果表明，通过对制造完成的首批样车进行离散化传递路径建模，在得到关门时的瞬态冲击载荷后，可以提前对后续同款车辆车门结构优化后的车内噪声进行声固耦合仿真预测，能够指导结构优化的方向，从而节省大量的人力物力，进一步促进了产品的开发流程。