一种改进的ELM-SAMME算法及应用研究∗

李克文 丁胜夺 段鸿杰

（1.中国石油大学（华东）计算机与通信工程学院 青岛 266580）

（2.中国石化胜利油田分公司信息中心 东营 257000）

1 引言

分类学习算法是机器学习中的一项热点研究内容，从传统的分类算法到新型的衍生算法，解决此类问题的方案层出不穷。黄广斌等［1］在单隐层前馈神经网络（Single-hidden Layer Feedforward Neural Network，SLFN）的算法基础上进行改进提出了极限学习机（Extreme Learning Machine，ELM）算法，针对传统反向传播（BP）神经网络［2］求解参数过多、神经网络训练时间消耗大、易陷入局部最优等缺陷，该算法以求解线性方程组的方法取代标准算法中梯度下降方法进行迭代求解的过程，求取最小二乘解得到输出层权值，简化了繁琐的迭代过程，形成一种速度快、结构简单、泛化性能好、人工干预少的学习算法。该算法常被用于解决分类、回归以及特征学习等问题。

Boosting方法［3］是一种经典的机器学习方法，在分类问题中，提升算法通过每次迭代的结果逐步的调整次轮训练样本的权重，将注意力转移到错分样本上，学习多个弱分类器后将这些弱分类器和相应迭代代数中获得的参数值进行线性组合，获得分类性能更强的强分类器。AdaBoost算法是行之有效的一种Boosting算法，它避免了标准Boosting中必须要预先计算各弱分类器分类准确率下限的麻烦，简化了模型求解过程，提升了算法实用性。经典的AdaBoost算法多被用于二分类问题的求解，而多分类问题在现实应用中更常见且其识别率更亟待提高。基于此，将AdaBoost算法扩展改进为多分类算法是一种可行的方案，现行的改进策略主要有两种［4］：一种方法是在标准算法的基础上进行结构扩展，例如AdaBoost.M1算法［5］，该改进算法要求每个分类器的分类正确率必须超过50%，这在多分类问题中对弱分类器的要求相对较高，会导致弱分类器的获取需要付出较大的时间消耗甚至无法集成至达到目标效果的集成分类器。AdaBoost.M2算法［5］也是一种直接扩展方法，相对于前者，该改进算法以误分样本权值和来代替错误率作为选取弱分类器准则，该改进算法降低了对弱分类器的要求，弱分类器的选取难度大大减小，同时提高了对错分和难分样本的关注度，但是，该举措同时增加了算法的时间复杂度，同时增加了退化现象发生的风险。Adaboost.MH［6］是另一种改进策略的代表算法，该算法将多分类问题分解为一定数量的二分类问题，弱分类器的获取相对容易，但该算法的改进思想同样提高了算法的结构复杂度及时间复杂度。针对上述缺陷，Zhu等［7］提出一种直接扩展多分类算法—多类指数损失函数逐步添加模型（Stagewise Additive Modeling using a Multi-class Ex⁃ponential loss function，SAMME），该改进算法改进了传统的AdaBoost算法中训练样本的权值重分配公式，把对弱分类器的基本要求降低到分类精度高于1/K（K为类别总数）即可，胡金海等［8］通过实验证明了SAMME算法的有效性，并将该改进算法用于发动机相关运行参数的数据挖掘实现故障诊断，并取得了良好的效果。SAMME算法虽降低了弱分类器的选择难度，但容易将一些效果较差的弱分类器集成到最终的强分类器中，造成强分类器的性能退化。

针对以上算法的不足，本文利用ELM极限学习机作为弱分类器，使用SAMME算法作为集成策略集成强分类器，并对SAMME算法的迭代过程进行改进，降低其容易引入较差弱分类器的风险，增强最终强分类器的分类性能。

2 ELM和SAMME算法

弱分类器的选取是提升方法中的关键，它决定了最终强分类器的组成，影响最终模型性能。合理有效的集成策略有助于增强最终强分类器的分类精度，使得最终分类模型在不同测试数据上的性能表现更加均衡。本节简要介绍ELM算法和SAMME算法，并进行总结分析。

2.1 ELM算法

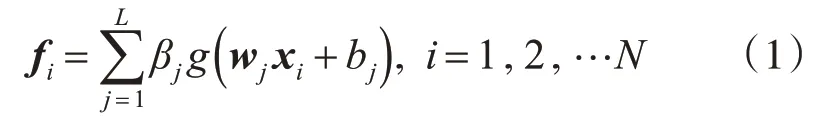
式（1）中，βj表示第j个隐层节点到网络输出节点之间的连接权值；wj=[wj1，wj2，…，wjn]表示输入节点和第j个隐层节点之间的连接权值向量；bj是第j个隐层节点的偏置。

为了求取最优的网络参数w和β，尝试最小化网络的预测输出和样本真实值之间的的差值使其为零，即，可转化为

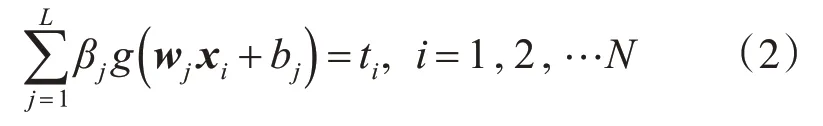
转化为矩阵形式为

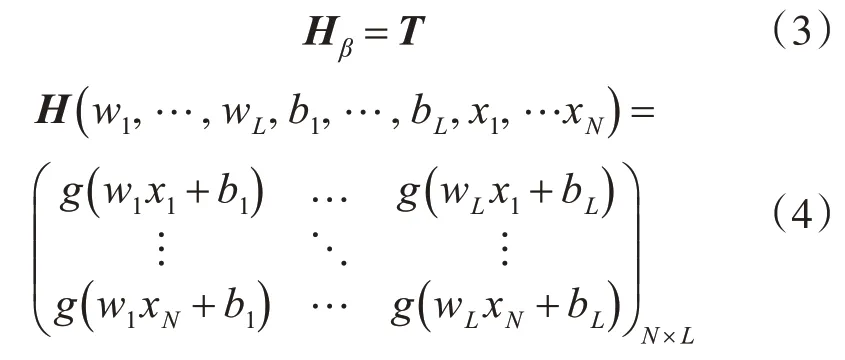
式（3）中，H表示网络隐含层的输出向量矩阵，矩阵中的第i列即为相应的隐层节点的拟合输出值；

在实际应用中，通常训练样本数N远大于算法隐层的节点数，当所选取的激活函数满足连续可微的条件，所求网络的隐含层参数w和b在训练过程中可以视为常数，无需调整网络中全部参数。然后上述模型可以通过求解最小化问题：得到权值向量β，根据广义逆原理，可计算得：

式（5）中，根据线性代数的求解法则需要求解H的广义逆矩阵H+，H表示隐层输出矩阵。

2.2 SAMME算法

提升（boosting）算法［9］的核心思想是在每一次迭代过程中，将注意力集中到错分样本上，提高错分样本的权重，使其在下一轮迭代中得到更多的关注，为了保持权值的平衡，相应的被正确分类的样本的权重会有下降。在集成策略中，分配给性能优异的基分类器较大的权重，使其在最终的结果表决中起到较大的作用。SAMME算法的操作流程［10］如下。

Step1给定含N个样本的训练数据集：( xi，yi)，xi∈Rn，yi∈(1 ，2，…，k)=Y，其中n为样本维数k为类别数，对训练样本权值进行等量初始化，并设定最 大 迭 代 次 数T D1=( w11，…，w1i，…w1N)，w1i=

Step2对t=1，2，…，T，执行1）～4）。

1）对经过Dt加权的训练数据进行训练，求得使伪误差率最小的弱分类器ht(x)；

2）计 算ht(x)的 分 类 错 误 率 ：

3）计算ht(x)的系数

4）训练数据集权值更新：Dt+1=(wt+1，1，…，wt+1，i，…wt+1，N)，其中，式中Zt为规范化因子，它使训练数据在下一轮迭代中的权值向量满足概率分布。

Step3构建所得弱分类器的线性组合，结合step2中式（3）所得系数得到最终强分类器：

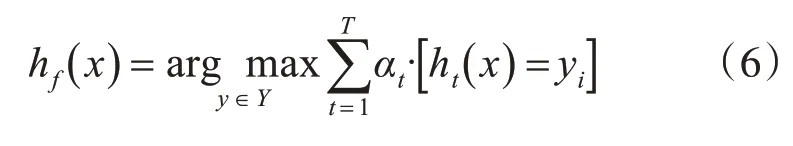
3 改进的ELM-SAMME算法

为了使SAMME算法在一定迭代次数下达到更优的分类精度，对该算法的样本权值及基分类器的权值分配过程进行改进，将该计算法记为IELM-SAMME，该算法的流程图如图1所示。

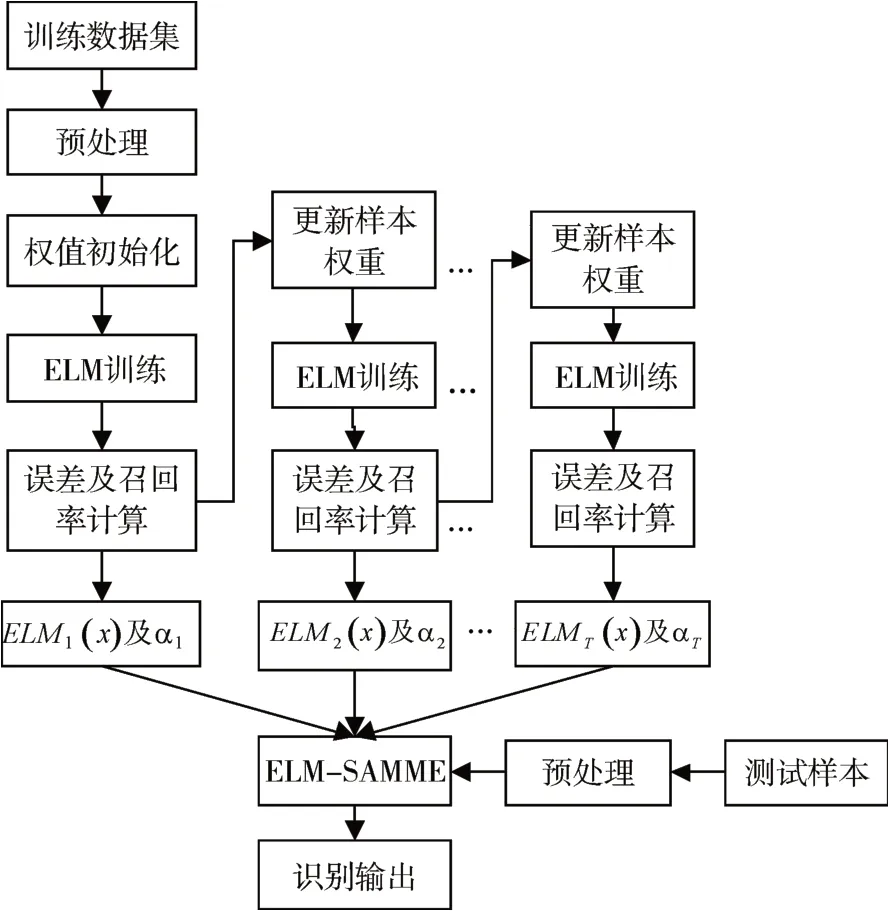
图1 IELM-SAMME算法流程

Step1对于给定训练数据集：( xi，yi)，xi∈Rm，yi∈(1 ，2，…，k)，其中k为类别数，初始化样本的权重：

Step2接下来的迭代过程t=1，2，…，T中，重复执行1）～4）。

1）将带有训练权重Dt的训练数据带入ELM模型进行拟合训练得到ht(x)。

2）计算相应的权重误差：

计算各个类别样本的召回率Rtk，比较得到最低的召回率min Rtk，将该类视为难分类，求取该类别样本在本次迭代中识别正确的样本权值和

3）根据ht(xi)在第t轮迭代中分类性能的表现，由2）中误差和召回率来决定此弱分类器权重分配：

4）为下次迭代更新样本权值：

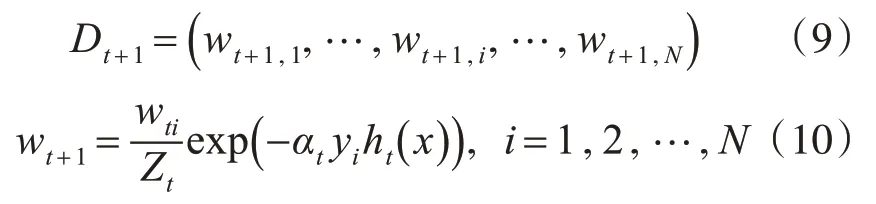
这里Zt为规范化因子，它使训练数据在下一轮迭代中的权值向量Dt+1成为一个概率分布。

Step3最终的强分类器可以通过对所得的弱分类器进行多数投票得到：

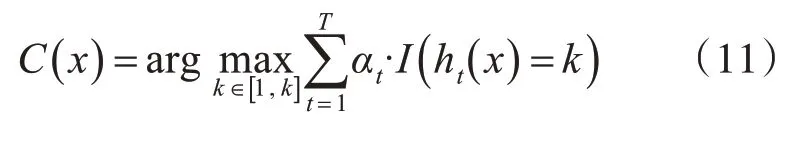
4 实验结果及分析

为了验证本文改进方法的可行性和有效性，在如表1所示的10个UCI公共数据集上进行实验，其中不平衡率为少数类样本与多数类样本数量的比值。将本文方法首先和极限学习机（ELM）算法、以SVM为 弱 分 类 器 的AdaBoost算 法［11］、标 准 的ELM-SAMME算法的进行结果进行比较，本文算法为IELM-SAMME。各方法的参数设置如下：ELM中，激活函数设置为sigmoid函数，隐层节点数L设置为 nl（n为输入节点数，l为输出节点数）；SVM-AdaBoost方法中迭代次数设置为10。ELM-SAMME及本文算法中的ELM参数同上，迭代次数同样设置为10。本文实验算法在8GB内存的Intel Core（TM）i7-6700CPU@3.4GHz的计算机上运行MATLABR2014b进行实验，实验过程中，为了减少初始化参数随机化对算法性能的影响，进行5次4折交叉验证，最后取各算法所有运行结果的均值进行性能比较。

在衡量各个分类算法在不同数据集上的分类性能表现时，仅仅选取准确率作为最终评价标准往往不能真实反映其分类性能，这是为了避免在不平衡数据集上最终评判结果的不公平性。在本实验中，选取G-mean和F1值作为实验结果的性能评价指标［12］，其定义如下：

最终实验结果如表2、表3所示，在表1所示的10个数据集上本文的IELM-SAMME方法G-mean值和F1值比单独使用ELM算法时取得效果都要好，这说明SAMME算法的应用取得了显著的成效，从结果中还可以看出改进方法尤其对不平衡率较高的样本集的识别效果有了较明显的提升。将改进方法与AdaBoost方法进行比较可以看出改进方法相比于AdaBoost方法在大部分数据集上都有提升，尤其在Ecoli等不平衡率较高的数据集上的提升尤为明显。而在平衡数据集如Iris上，改进方法获得了与传统方法相当的水平。该方法与未改进的ELM-SAMME算法进行比较仅在Iris、Wine等数据集上略差于ELM-SAMME方法。

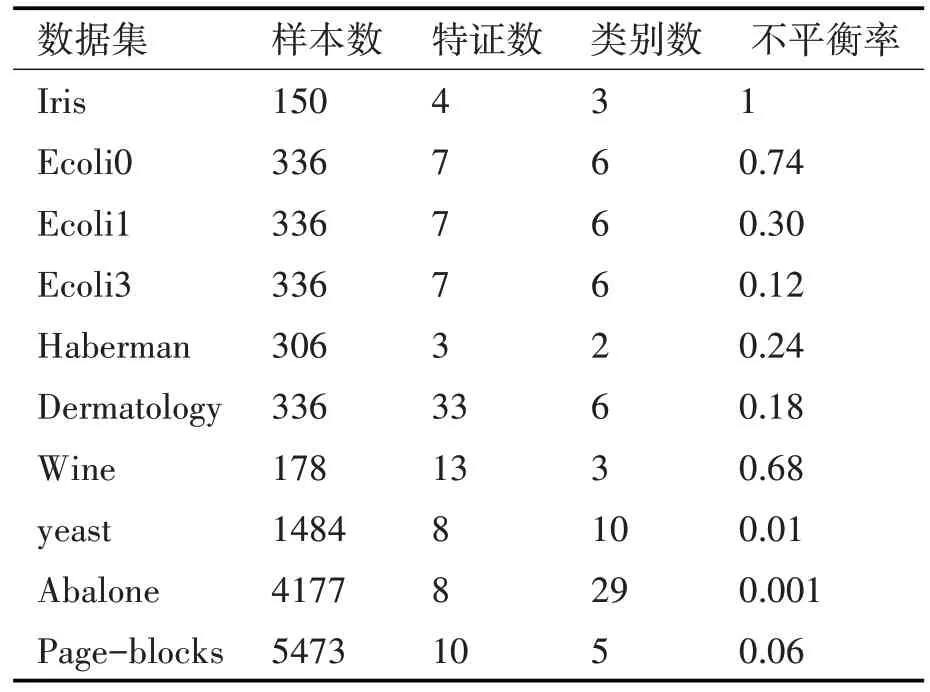
表1 15个UCI数据集及其相关特征

表2 各算法在10个数据集上的平均G-mean值

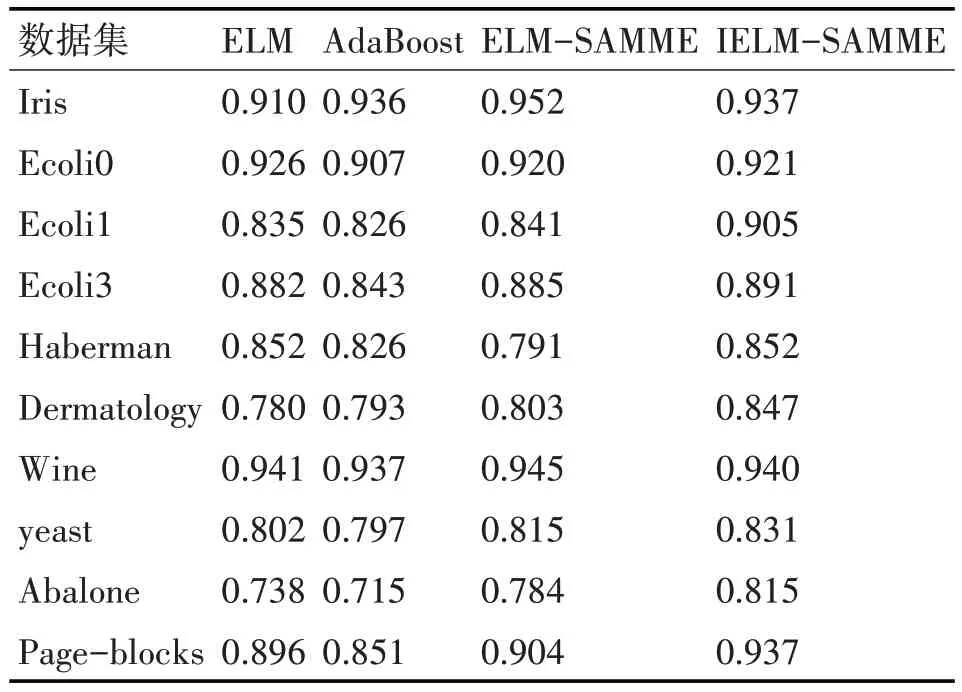
表3 各算法在10个数据集上的平均F1值

经以上对比实验证明了该算法的有效性，然后使用该算法和现行分类算法进行比较。此组对比实验仍然在表1的10个UCI公共数据集上进行，实验结果的性能指标仍然使用G-mean值和F1值来评判。此组对比实验加入Over-Bagging［13］、Under⁃Bagging［14］、EasyEnsemble［15］等算法，实验结果如表4、表5所示。由实验结果可知，该改进方法在其中的6个数据集上均取得了更好的G-mean值，在7个数据集上得到了更好的F1值。在Iris、Ecoli1、Haberman等数据集上的G-mean仅次于最优值或近似最优值，在Haberman、wine等数据集上的F1值仅次于最优值。这可以解释为在类如Iris的数据集上样本数量相对较少且各类样本比率相对平衡，各个算法模型较容易达到较好的拟合效果，此时各个算法的性能表现极有可能出现持平或存在较小的差距。而改进算法在样本量适中或者较大的数据集上表现较为稳定和高效，尤其在不平衡率较高的yeast、Abalone等数据集上获得了较其他算法都要好的效果。

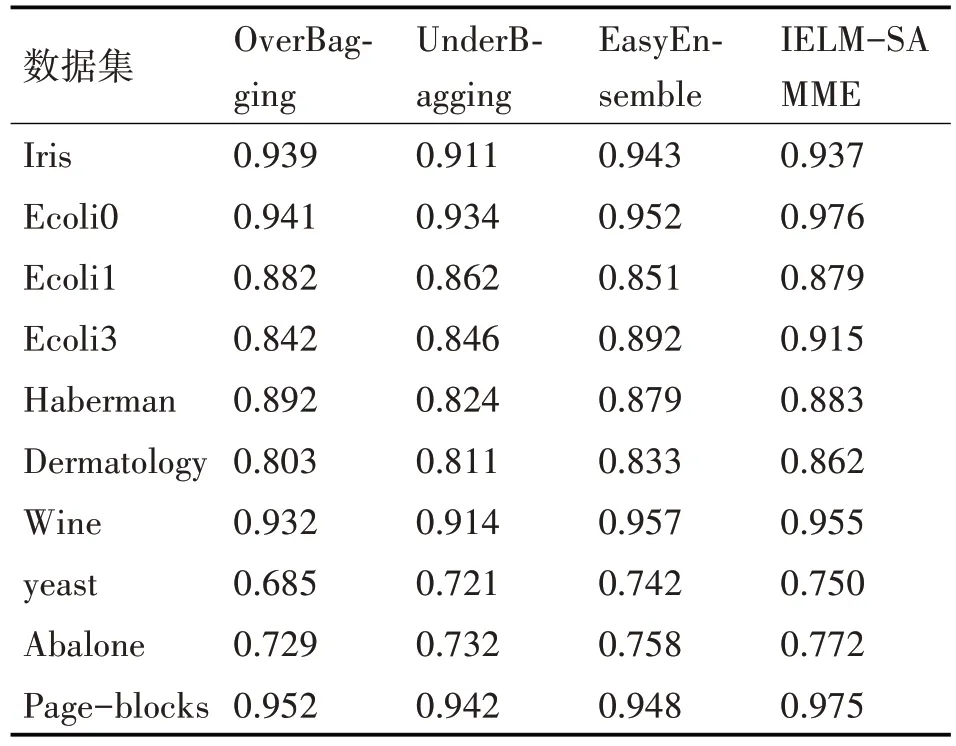
表4 各算法在10个数据集上的平均G-mean值

表5 各算法在10个数据集上的平均F1值

5 结语

本文以极限学习机为弱学习器，以SAMME算法为集成策略，在标准的SAMME算法的基础上进行了有针对性的改进，提升了算法对数据集中召回率最低的种类数据的识别敏感度，增强了算法在众多数据集尤其不平衡率较高的数据集上的分类性能，为进行相关分类研究的进行提供了参考。相比于其他算法，该算法中基学习器的计算消耗较大，集成算法的时间消耗以及执行效率都有待提高。此外，尽管目前针对极限学习机的一些分类算法被提出，但是将其应用于不平衡数据的分类应用相对较少，将极限学习机算法扩展到半监督和无监督学习任务的研究极少，以上都是有待解决的问题。