基于相似度的蚁群聚类算法∗
2021-06-29沈兴鑫杨余旺肖高权徐益民陈响洲
沈兴鑫 杨余旺 肖高权 徐益民 陈响洲
(1.南京理工大学计算机科学与工程学院 南京 210094)
(2.湖南云箭集团有限公司 怀化 419500)
1 引言
聚类[1](Clustering)是一种重要的数据挖掘分析方法,主要目标是在海量数据中找出相似的数据并按照相似度分为不同的类,从而使得一个集群内的数据项彼此相似,不同集合中的数据尽量不同。从生物学到社会学再到计算机科学等众多领域都存在相同的需求,因此聚类算法得到了广泛的应用。
蚁群聚类(Ant Colony Clustering)是一种受蚁群启发的聚类算法。意大利学者Dorigo M[2]在模仿蚂蚁群体行为的基础上提出了蚁群算法,根据蚁群的信息素机制寻找蚁穴和食物间的最短路径,并有效地解决TSP问题。Deneubourg J[3]基于人工蚁群模型结合蚂蚁的堆尸行为提出了聚类算法(Basic ant colony clustering model,BM)。Lumer E D和Fa⁃ieta B[4]在BM模型的基础上改变蚂蚁移动速度提出了LF模型,很好地解决了大数据量时的聚类问题。
相比于其他的聚类算法,蚁群聚类有以下几个优点,如灵活性、鲁棒性、分布性和自组织性。因此该算法被更多的人研究并改进。Bin W和Zhong⁃zhi S[5]研究了相似系数,并提出了一种更简单的概率转换函数。王慧和甘泉[6]加入了参数自适应调整策略,提高了蚁群聚类的准确性。乔少杰[7]研究了蚁群的分布式模型在文本聚类中的应用。Tan S C等[8]提出了一种简化的基于蚂蚁的聚类方法,该方法基于现有的基于蚂蚁的聚类系统的研究。林金灼[9]结合了主成分分析方法(Principal Compo⁃nent Analysis,PCA),提高了蚁群的聚类质量。Tao等[10]重新定义了两个数据对象之间的距离,并改进了蚂蚁丢弃和拾取数据对象的策略,从而提出了一种改进的蚁群聚类算法。Xu X等[11]提出了一种约束蚂蚁聚类算法,该算法嵌入了基于随机游走的启发式步行机制,以解决约束聚类问题。张梦佳[12]采用实时信息素更新规则,提高了蚁群聚类的收敛速度,同时提高了准确度。周峰[13]提出一种结合蚁群聚类和模糊均值聚类思想的聚类算法算法,该算法具有全局优化能力,优化了蚁群聚类易陷入局部最优的缺点。赵宝江[14]利用蚁群聚类算法来进行结构辨识,确定系统的模糊空间和模糊规则数,实现非线性系统的辨识,辨识精度高,可当作复杂系统建模的一种有效手段。
虽然以上方法优化了蚁群聚类算法,但是蚁群聚类前期收敛速度慢的问题未有效的解决。由于蚂蚁随机移动数据项的位置存在多次无效的移动,导致算法计算效率和准确性较低,对于复杂的工程,该问题更为突出。为克服这些缺点,本文提出了一种新的蚁群聚类算法,通过添加相似度矩阵将原算法中蚂蚁随机移动修改成按照相似度矩阵有目的地移动,蚂蚁随机关联修改成有目的地关联。通过实际数据集验证了新算法的性能,并与先前研究中提出的蚁群聚类算法和其他算法进行了比较,验证了新算法的有效性。
2 蚁群聚类算法
蚁群聚类算法是一种群体智能方法,受到蚁群堆积尸体和排序幼虫行为的启发而形成的一种聚类方法。因其灵活性、鲁棒性、分散性和自组织性等特点被广泛研究。
2.1 LF算法基本原理
在LF模型中,将蚂蚁的尸体建模为需要聚类的数据项,蚂蚁建模为在环境中随机移动的代理,蚂蚁移动的平面建模为一个具有边界条件的二维网格。分散在平面中的数据项通过代理拾取、搬运和放下从而将相似的数据项放在一起。数据项的取放概率受到该数据项与邻域内其他数据项的相似性和密度的影响,在拾取时,相似度越低越有可能拾取,相反,在放下时,相似度越高越可能放下。因此在网格上对数据项进行排列,使得相似度越高的数据项在平面上越靠近。
2.2 蚁群聚类算法模型
首先,将N个数据项随机地映射到一个M×M的二维平面中,并将E只蚂蚁分散到数据平面中并为每只蚂蚁ei关联一个数据项,即形成蚂蚁到数据项映射:

其中E是蚂蚁集合,N是数据项集合,F是蚂蚁到数据项的随机映射函数。
再计算出当前数据项与邻域内其他数据项的相似度f(ei),相似度计算式(2)所示。
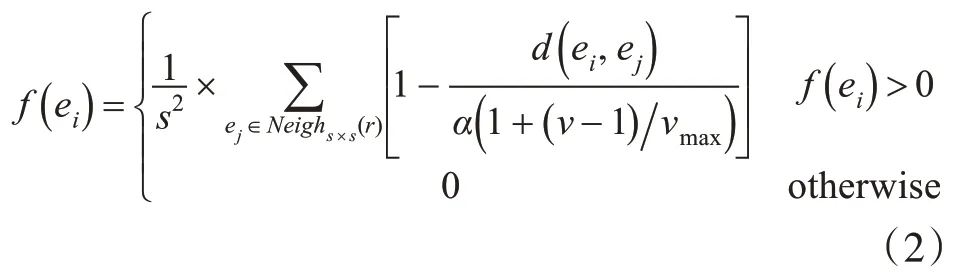
其中α是自定义的参数,用来调节蚂蚁间的相似度。V定义了蚂蚁的移动速度,vmax代表了最大速度,V随机分布在[1 ,vmax]中。s是自定义的蚂蚁的搜索长度。Neighs×s(r)代表位置r的周围s×s面积。d( ei,ej)是ei和ej之间的距离。d( ei,ej)采用欧式距离,公式如下:
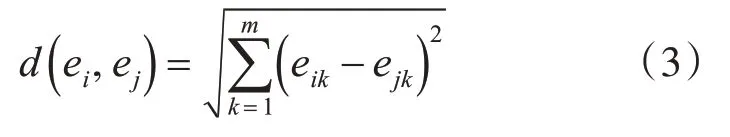
其中m是数据项的维度。
当蚂蚁处于空载状态需要拾起数据项时,按照如下公式计算拾起概率pp:
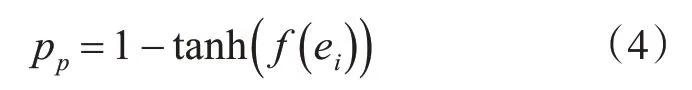
其中f(ei)是ei的相似函数,tanh(x)函数的定义如式(4)所示。

其中c为自定义的常量,用来调节算法汇聚的速度。
当蚂蚁处于负载状态需要放下数据项时,按照如下公式计算放下概率pd:

tanh函数和pp概率曲线图如图1所示。
在本模型中,蚂蚁在拾起或者放下数据项后随机移动,数据项与领域内的数据项相似度可能不高,因此下次被移动的概率又会增加,从而降低了聚类的速率。同时,当负载的蚂蚁放下数据项或者空载的蚂蚁没有拾起数据项而需要重新关联数据项时,数据项的关联也是随机的,增大了再次关联的概率,导致聚类速率降低。
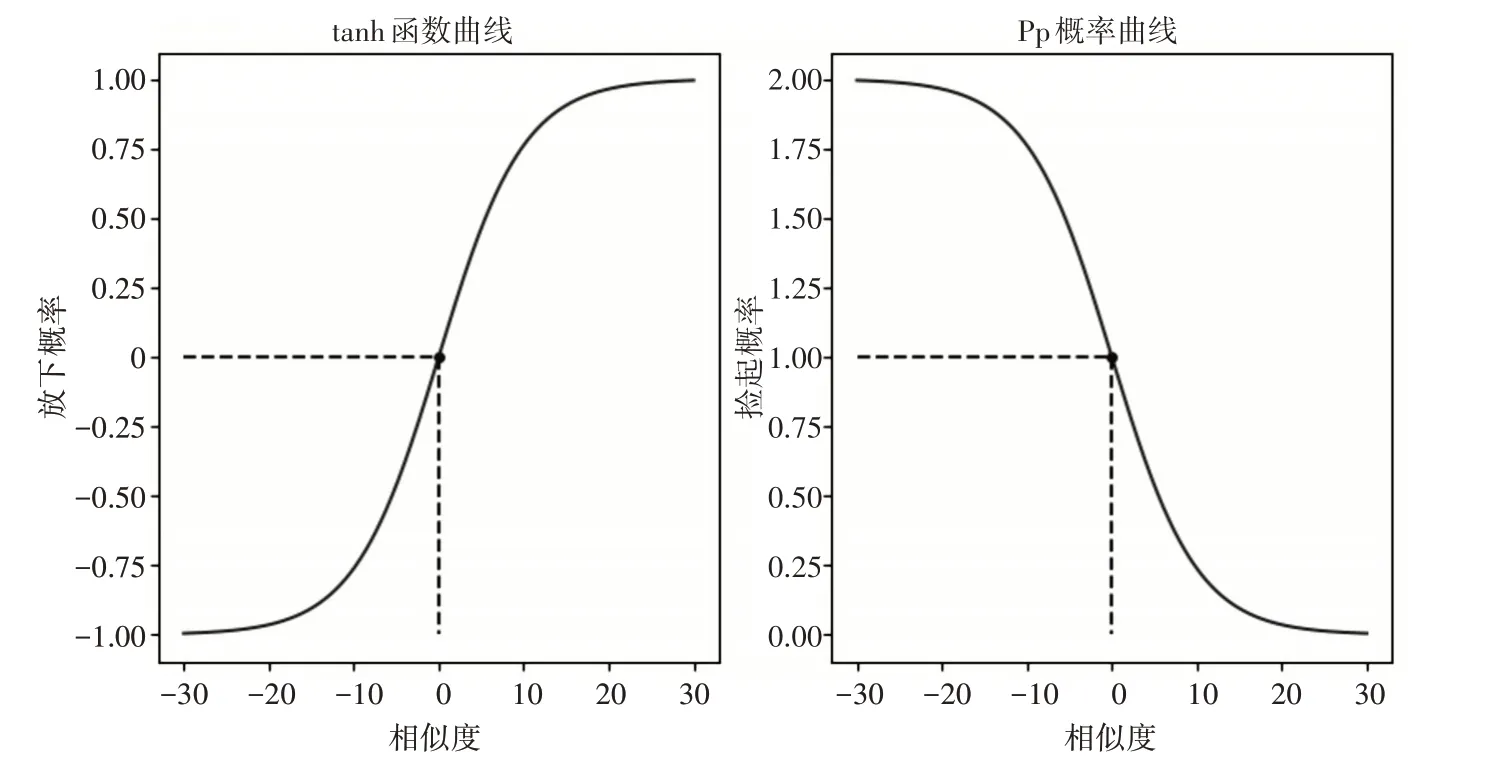
图1 tanh函数图和pp概率曲线图
针对以上两个缺点,本文在原有算法基础上设计了相似度矩阵,让蚂蚁按照相似度有目的地移动,同时在蚂蚁需要映射数据项时,根据相似度矩阵有选择的映射,从而加快聚类的速度。
3 改进的蚁群聚类算法
传统的蚁群算法移动蚁卵或者关联蚁卵时都是随机,存在无效移动与映射,导致聚类效率降低。改进的蚁群聚类算法在原有算法基础上设计了相似度矩阵,蚂蚁按照相似度有目标地移动,同时有选择地映射到数据项,从而加快聚类速度。
3.1 算法原理
蚁群聚类通过蚂蚁移动数据项,使相似度高的数据项在平面上尽可能靠近,从而形成聚类簇。在此过程中,将数据项移动到相似度高的区域附近可以大幅提高聚类速度。蚂蚁因放下或者未能拾起数据项时需要重新关联数据项。此时,当前数据项和邻域的相似度较高,需要移动的概率较低,因此,关联相似度低的数据项,增加操作次数可以提高聚类效率。
3.2 算法实现过程
3.2.1 建立相似度序列矩阵
首先计算每个数据项和其他数据项之间的距离。由于余弦相似度计算简单、直接,对于单独判断两个数据对象的相似度准确率高,因此本算法采用余弦相似度来计算数据项间的距离,其定义如下:

其中ei、ej表示两个不同的数据项,eik、ejk表示不同数据项所代表的矢量坐标值,n表示数据项的维度。
然后对余弦距离标准化,形成相似矩阵(Simi⁃larity Matrix)。该矩阵是一个N×N的对称矩阵,表示N个数据项两两之间的相似度,形如:

其中,dij是数据项i和对象j之间余弦距离的标准化表示。当数据项i和数据项j越相似,其值越接近0;相反,两个数据项越不同,其值越接近1。
再以相似矩阵为基础,以列为单位,按照相似度从高到地的顺序进行排序,形成相似度序列矩阵,形如以下公式:

其中函数f(x)是以矩阵x为参数的快速排序函数,sij表示与第i个数据项相似度排序第j个的数据项的序号,sij∈(1…n)。数据项与该数据项的 相 似 度 最 高 ,因 此 [s11s12…sn1]=[1 2…n]。
3.2.2 提高蚂蚁的移动目的性
在蚂蚁移动数据项时,首先根据以下公式确定当前数据项的邻域。
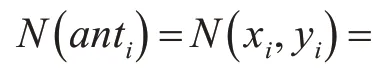
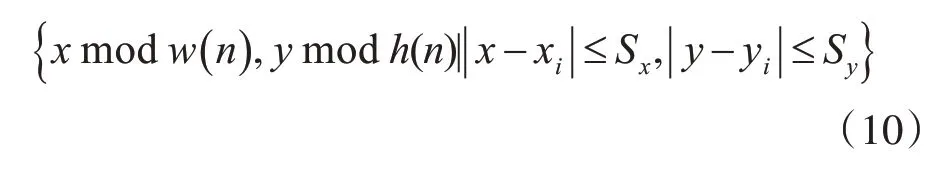
其中anti表示第i只蚂蚁,位于( xi,yi),Sx和Sy分别代表该蚂蚁水平方向和竖直方向的视野。数据项领域如图2所示。

图2 数据项领域范围
然后确定邻域中的数据项,即ej∈N( anti),再按照相似度序列矩阵找出邻域中相似度最高的数据项,将当前数据项移动到该数据项附近。
Algorithm1:Similar Move
1)Input:Index of current spawn
2)Ouput:Index of most similar spawn
3)Calculate Neighbor Area(N(oi))
4)Get column i of Indexmatix
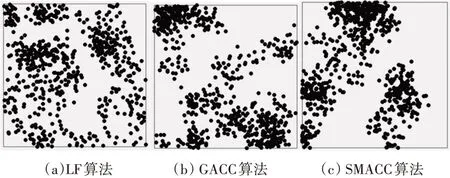
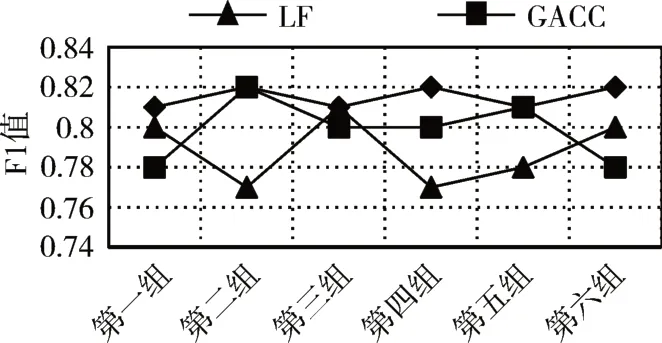
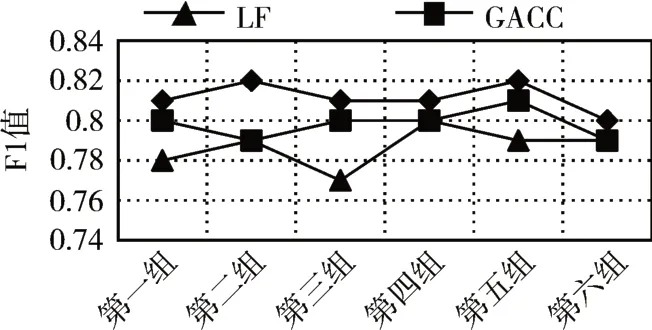
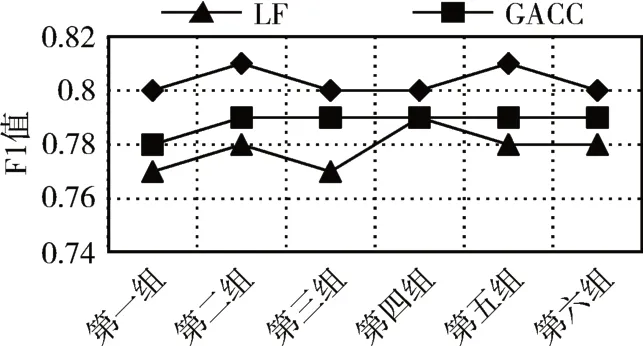
5)For j=1;j 6)k←Indexmatix[i][j] 7)If okϵN(oi) 8) Move oinearby ok 9) Return k 10) Else 11) Continue 12) End if 13)End for 14)Return Spawn number-1 3.2.3 增加关联的目的性 按照相似度序列矩阵找到和当前数据项最不相似的数据项并映射到该蚂蚁,伪代码如下: Algorithm2:Dissimilar Mapping 1)Input:Index of current ant i 2)Output:Index of most dissimilar spawn k 3)Get column i of Indexmatix 4)For j=Spawn number-1;j>=1;j-- 5)k←Indexmatix[i][j] 6)If oknot occupied 7) Map current antito ok 8) Return k 9)Else 10) Continue 11)End if 12)End for 为验证改进算法的有效性,本文设计了仿真实验,通过不同数据集和不同算法的实验结果对比,验证了本算法的有效性。 实验所用的数据集:本实验采用了UCI数据集中最常用的Iris,Wine,Haberman,Balance-scale数据集,数据集的简介如表1所示。 表1 样本参数 本文的算法采用了相似度矩阵(Similarity Ma⁃trix)提高算法的聚类效率,记改进的蚁群聚类算法为SMACC(Similarity Matrix Ant Colony Clustering)。 用LF算法,文献[15]中的GACC(GAnt Colo⁃ny Clustering)算法和SMACC算法对Iris,Wine和Haberman数据集进行聚类,在同样迭代4000次的情况下,运行结果分别如图3、图4、图5所示。由结果可以看出,对Iris,Wine和Haberman数据集迭代4000次后,SMACC算法聚类结果最明显,GACC算法有明显的聚类趋势,而LF算法仅有聚类趋势,这表明本算法相对其他两种算法有较高的聚类效率。Balance-scale数据集的样本个数远大于其他数据集,在迭代4000次后很难比较聚类的效果,图6是三种算法迭代10000次后Balance-scale数据集的聚类结果。结果可以看出,SMACC在大数据集的聚类效果明显优于其他两种算法。 图3 Iris数据集 图4 Wine数据集 图5 Haberman数据集 图6 Balance-scale数据集 Iris数据集和Wine数据集有相似的样本个数,但Wine数据集的属性个数远大于Iris数据集的属性个数。比较图1和图2可知,属性个数增加,聚类效果有所降低。但是,由于SMACC算法采用余弦距离计算数据项间的相似距离,余弦距离更有利于区分高维度的数据项,因此,SMACC在高维度数据项的聚类效果远优于其他两个算法。在相同的迭代次数下,Iris数据集的聚类效果比Wine数据集的聚类效果好。 在一次迭代过程中,如果放下或者未捡起数据项的蚂蚁数量占总量的90%时,表明聚类基本完成。三种算法分别在四种数据集上收敛时的六次平均迭代次数如表2所示。 如表2所示,使用相同数据集时,SMACC的平均迭代次数明显小于其他两种算法,该结果表明本算法有效地提高了聚类速度。Balance-scala数据集中,SMACC的迭代次数远小于其他两种算法,说明该算法更适用于大数据集的聚类。 表2 平均迭代次数比较 F-measure从查准率和查全率综合的角度衡量聚类算法的结果。其一般形式如式(2)所示: 其中,β是查准率和查全率的权重比,P是查准率,R是查全率。 本文采用F1值比较四种数据集上三种算法的聚类效果,结果如图7~10所示。 图7 Iris数据集 图8 Wine数据集 图9 Haberman数据集 图10 Balance-scale数据集 比较三种聚类算法对四种不同数据集的F1值,GACC和SMACC算法与LF算法的聚类效果总体相似,但GACC和SMACC略好于LF算法。随着数据集中样本数量的增加,三种算法的F1值总体有所下降,由于SMACC算法在蚂蚁移动的过程中有目的地移动,所以数据簇中相似度总体比较高,所以在Balance-scale数据集中F1值明显高于LF和GACC算法。同时,由于蚁群聚类是基于群体行为的聚类方法,随着数据量的增加,聚类结果的波动也减小。图8中,由于数据的维度增加,样本的区分度有所降低,但SMACC采用余弦距离作为相似距离,所以F1值略高于其他两个算法。 蚁群聚类是一种利用群体智能的聚类算法,其灵感来自蚁群聚集其尸体的行为。该算法具有鲁棒性强,适合分布式等优点,但是因为蚂蚁随机移动数据项而造成多次无效移动以及资源浪费。针对该问题,本文设计了相似度矩阵,使蚂蚁在相似度矩阵的指导下有目的地移动和关联,从而加快聚类速度。 仿真实验中,对比了本算法和其他两种算法对UCI数据集中四个实际数据集(Iris,Wine,Haber⁃man,Balance-scale)的聚类性能。结果表明,新的蚁群聚类算法在保证聚类精度的基础上,能够以较高的速度解决聚类问题,同时具有很好的计算稳定性。但是SMACC依然存在局部优化的问题,在接下来的工作中希望通过参数的动态调整来解决该问题。4 实验结果与分析
4.1 实验环境与实验数据集

4.2 实验结果与分析




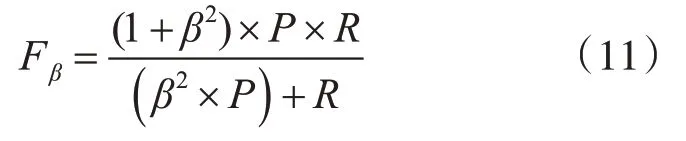

5 结语
