基于双曲切比雪夫逼近的光谱模板构造∗

于 苗 蔡江辉 杨海峰

（太原科技大学计算机科学与技术学院 太原 030024）

1 引言

郭守敬望远镜（LAMOST）［1～4］是一种特殊的反射施密特望远镜，有效孔径为3.6m～4.9m，焦距为20m，视场为5°，其焦面上可防止4000根光纤，因此在一次曝光中LAMOST可以同时观测到4000条光谱。在恒星和星系的科学研究方面，LAMOST有着巨大的研究前景和价值。LAMOST巡天得到的光谱复杂多样，有各种类型的光谱。对天体光谱的分析首先需要进行光谱的自动识别，因此研究恒星自动识别与分类方法具有重要意义［5～6］。

恒星自动识别与分类系统的正确率和可信度取决于恒星光谱模板库的质量。目前常用的恒星光谱模板库主要有MAFAGS［7］、MARCS［8～11］、Kurucz理论模板库［12］。MAFAGS模板库是一套步长较细的网格光谱数据，MARCS模板库只包含F、G、K型星模型并且对冷星更适用，Kurucz模板库是恒星大气模型网格数据。共包含约9561个模型，大部分为正常恒星模型。该恒星理论光谱库的构建分成两部分包括大气模型的计算和理论光谱的合成，即从大气模型的输入量：表面有效温度Teff、表面重力加速度g、元素丰度（［M/H］）到光谱的输出量：流量（x），波长（λ），这是一个非常复杂的非线性映射过程。

上述三种恒星模板库的构造方法适用于所有来源的恒星光谱来构造相应模板库。然而将其运用于LAMOST巡天得到的恒星光谱数据时并不能很好地对恒星光谱数据进行自动识别和分类。基于以上缺陷，韦鹏［13］等在构造了包含183条模板光谱，61个不同的子类型的适用于LAMOST的恒星光谱模板库，该模板库是韦鹏从约100万条LA⁃MOST DR1恒星光谱数据中经过一系列操作筛选出来的，被广泛应用于LAMOST光谱分类工作中，该模板库的构造方法复杂。

上述现存的恒星理论光谱模板库构造方法较为复杂，给恒星光谱自动识别和分类带来了一定的困难。因此本文提出了一种基于切比雪夫双曲线逼近的恒星光谱模板构造方法。该方法首先将光谱数据分段，分为多个小光谱段，得到具有多个波段并提取波长流量信息，然后依据波长流量信息基于切比雪夫双曲线逼近提取每类光谱数据特征谱线的形状特征，最后将提取出的光谱数据特征谱线的形状特征与标准光谱特征谱线比较。

2 理论基础

2.1 函数逼近与一致逼近

函数逼近［14］就是用简单函数逼近已知的复杂函数。通常步骤为首先通过复杂函数在有限点集上给定函数值，再在包含该点集的区间上用公式给出函数的简单表达式。即对于函数类A中给定的函数（fx），要求在另一类较简单的便于计算的函数类B中找到一个函数p（x），使p（x）与（fx）的误差在某种度量意义下达到最小。函数类A通常是区间［a，b］上的连续函数，记作C［a，b］，而函数类B通常为n次多项式等。

将函数逼近问题中的逼近函数与给定函数之间的逼近方式给出一种定义，换言之，一致逼近［15］是度量连续函数（fx）和逼近多项式p（x）之差的一种标准，即对于区间［a，b］上的连续函数（fx），对于给定的任意小正数ε>0，存在多项式p（x），使不等式

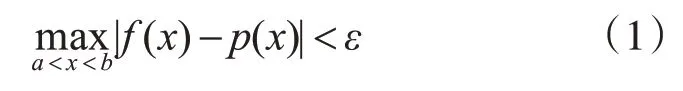
成立，则称多项式p（x）在区间［a，b］上一致逼近于函数（fx）。显然，如果精确度越高，即ε越趋近于0，则用来逼近的多项式p（x）的次数一般也越高。

2.2 切比雪夫逼近

切比雪夫逼近［16～17］是切比雪夫基于一致逼近提出的确定逼近的最快的多项式的方法。切比雪夫逼近的思想是：不让逼近多项式的次数n趋向于无穷大，而是先把n固定。

定义（偏差）：次数不超过n次的实系数多项式的集合为pn，p(x)∈pn，f(x)∈C[a，b]，f(x)与p(x)的偏差定义如下：

定义（切比雪夫逼近）：对于函数f(x)，在pn中寻找一个多项式p*n(x)，使其满足：

此时p*n(x)对f(x)的偏差和其他任一p(x)对（fx）的偏差比较时是最小的，我们称p*n(x)为f(x)在［a，b］上的切比雪夫逼近。

在切比雪夫逼近中，逼近多项式p*n(x)的选择很多种，包括代数多项式、三角多项式以及有理分式函数等。

3 基于切比雪夫双曲线逼近的分段式模板构造方法

3.1 切比雪夫双曲线逼近

显然，切比雪夫逼近定义是用一个多项式逼近一个连续函数。将切比雪夫逼近的思想扩展到用一个多项式逼近一组连续函数，得到该组连续函数的切比雪夫逼近多项式，可描述为对于区间［a，b］上的l个连续函数f1(x)，…，fl(x)，p*n(x)为该组连续函数的切比雪夫逼近，则p*n(x)满足：

此时，pn*(x)对每一个连续函数fi(x)的偏差和不超过n次的实系数多项式的集合pn上其他任意多项式p(x)与fi(x)的偏差相比时都是最小的。

因为任意曲线都可通过拟合近似表示得到函数表达式，因此将每个连续函数fi(x)看作区间［a，b］上的曲线Si(t)，那么对于l个连续函数求切比雪夫逼近就转化为对l条曲线求最佳逼近。在此基础上，切比雪夫双曲线逼近最初来源于上述对多条曲线的切比雪夫逼近。其中心思想是将对多条曲线的切比雪夫逼近等价到对两条曲线的切比雪夫逼近上，这两条曲线分别是最大值曲线和最小值曲线。此时式（4）可转化为

每一条曲线与最佳逼近之间的偏差最小简化为最大值函数或最小值函数与最佳逼近之间的偏差最小。其中，Smax(t)为该组曲线在区间［a，b］上的最大值曲线，其定义为

Smin(t)为该组曲线在区间［a，b］上的最小值曲线，其定义为

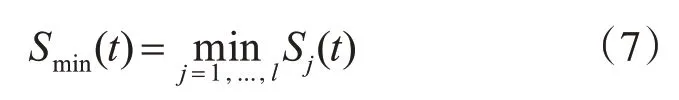
S*(A，t)为该组曲线的切比雪夫双曲线逼近。得到S*(A，t)的方法是先用函数来假设该最佳逼近，然后求出系数的值，具体的函数表达式就可知了。用函数形式表示最佳逼近，假设最佳逼近的形式表示为

此外，为求解式（5）引入一个变量z，该变量z表示任意一条曲线与最佳逼近间的最小差值，其表示为

此时，解决上述最佳逼近函数的问题转化为解决线性规划的问题。该线性规划可表示如下：

目标函数为

约束条件为

通过求解该线性规划问题可得最小偏差z和最佳逼近函S(A，ti)。

3.2 算法描述

基于切比雪夫双曲线逼近的分段式恒星光谱模板构造方法，将所有光谱按类分组，相同类型的恒星光谱视作一组并提取各组光谱的波长和流量信息，对每一组光谱数据进行分段，使每一组光谱分为具有若干段的同类型光谱组，对于各段的波长流量信息，将波长作为自变量，流量作为因变量，得到相关曲线。对每一条曲线进行归一化，再分别通过式（6）、（7）计算该组曲线的最大值曲线和最小值曲线。引入变量z，用多个未知参数和多项式基的代数和的形式表示该组光谱的切比雪夫双曲线逼近，用最大值曲线、最小值曲线和式（9）定义变量z，运用式（10）、（11）线性规划的方法在每段光谱上做切比雪夫双曲线逼近，得到各组的整体态势。具体步骤如下。

算法：基于切比雪夫双曲线的恒星光谱模板构造方法

输入：LAMOST数据集D，光谱类数X，分段长度T，光谱维度W

输出：各类恒星光谱模板

1）对每条光谱归一化

2）将每条光谱按T分段，总段数为S

S=「W/T⏋

3）for x=1 to X do

4） 根据式（6）、（7），计算得到Smax（t）and Smin（t）

5）for s=1 to S do

6） 根据式（10）、（11），计算min z，S(A，ti)

7） end for

8）end for

9）该组光谱的切比雪夫双曲线计算完成

本文的算法内容主要包括两个部分，第一部分是光谱数据分段，第二部分是在每类已分段的光谱数据实现切比雪夫双曲线逼近。光谱数据分段的时间复杂度为O（n），实现切比雪夫双曲线逼近的时间复杂度为O（n2），算法的整体时间复杂度为O（n2）。

4 实验分析

在1台Inter（R）core（TM）i7-6500U@2.50GHz笔记本电脑，Windows 7操作系统中使用Python语言在PyCharm平台实现了基于切比雪夫双曲线逼近的分段式恒星光谱模板构造方法。

4.1 实验数据选择

本实验主要在LAMOST DR5恒星光谱数据上进行实验得到适用于lAMOST恒星光谱数据的恒星光谱模板。每条LAMOST光谱数据都有相应的波长和流量信息，波长范围在3700～9000。本实验选取原本由pipeline分类得到的A、F、G、K、M五类恒星光谱数据，信噪比不低于20。具体数量如表1所示。

表1 恒星数据情况

4.2 实验结果与分析

4.2.1 各类恒星模板光谱

本实验在上述数据集上进行操作，得到的各类恒星模板光谱如图1～5所示。

图1 A型光谱模板

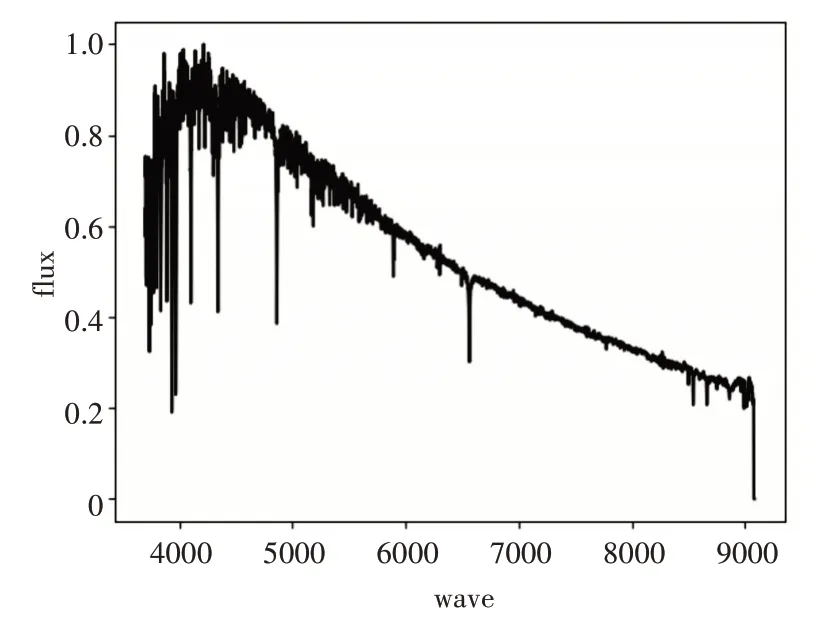
图2 F型光谱模板

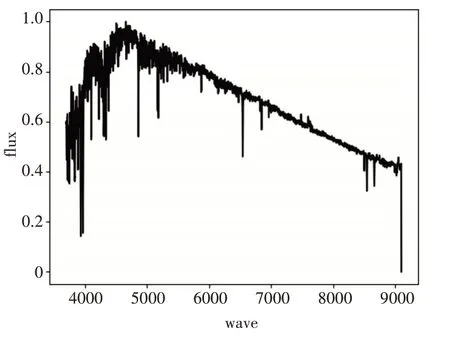
图3 G型光谱模板

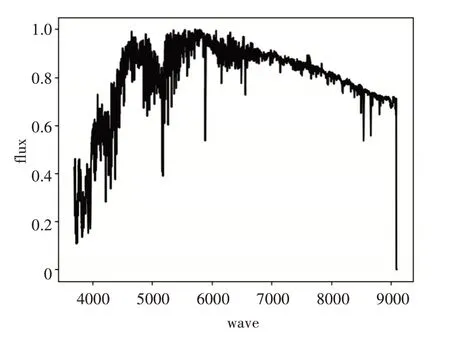
图4 K型光谱模板

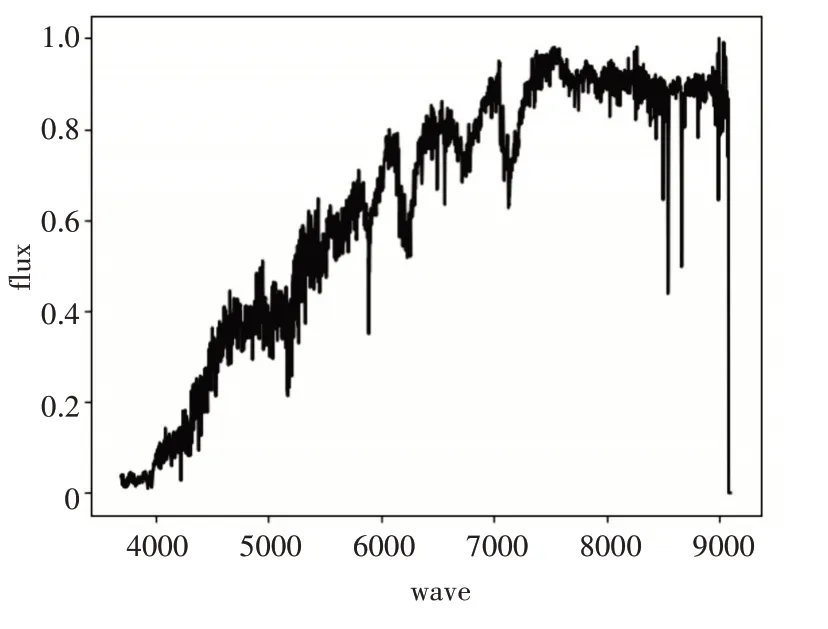
图5 M型光谱模板

4.2.2 整体态势分析

从上述模板光谱中看出不同类型的恒星光谱模板谱整体走势是不相同的，具有明显的差异性。具体分析图1～5，从A型光谱到F型光谱再到G型光谱，大致来看蓝端高红端低并且峰值逐渐向红端移动。K型光谱，已经变成红端高蓝端低，再到M型光谱完全变成红端与蓝端的差距加大，并且蓝端变得非常高。上述计算所得的各类恒星光谱模板谱的整体态势与互相过渡变化满足各类光谱整体走势理论。因此，本文所提方法构造的恒星模板谱具有可信度。

4.2.3 与其他光谱模板的比较（数量）

该实验在A、F、G、K、M五种恒星光谱数据情况下实验具体选取了A1IV、F0、G0、K0、M0共5个子类的数据。在现行的韦鹏等构造的183恒星光谱模版中，子类A1IV的模板谱数量为4，子类F0的模板谱数量为4，G0的模板谱数量为2，子类K0的模板谱数量为3，子类M0的模板谱数量为10。每一个子类的模板谱的数量皆大于1条。然而运用上述方法对每一个子类恒星光谱都可以得到唯一一条模板谱。模板谱数量减少，大大提高了恒星自动识别和分类的效率。

5 结语

本文提出了一种切比雪夫双曲线逼近的分段式恒星光谱模板构造方法，该算法采用将整条的光谱划分为多段子光谱，提取其相应的波长和流量信息，并得到光谱的最大值曲线和最小值曲线。通过切比雪夫双曲线逼近利用偏差的最小值z和最佳逼近的代数表达式，最大值和最小值曲线通过线性规划的方法得到一组曲线的切比雪夫双曲线逼近，将其作为该类恒星光谱的模板谱，最终通过该方法得到恒星光谱的模板谱。采用恒星光谱数据集验证了方法的有效性。本文下一步的研究方向为考虑如何能提高算法的运行速度，加快实现各子类恒星光谱模板谱的构造。