伙伴学习,思维在不同层次的学生中悄然发生
——《解决问题的策略》教学设计
2021-06-25文|袁园
文|袁 园
【教学内容】
苏教版五年级下册第七单元。
【教学过程】
一、我会思考-交流中明晰策略
出示例1:
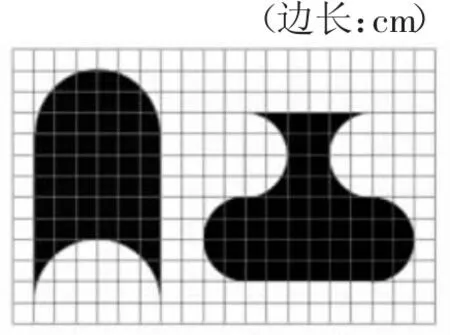
师:今天我们一起来研究解决问题。这有两个图形,你能一眼看出哪个面积大一些吗?
生:不能。因为这两个图形看起来比较复杂,有些地方还是有弧度的,我不会直接比较。
师:看来直接比较似乎有点困难,你能想到什么策略来解决这个问题呢?
【设计意图:课始,以复杂的图形比较大小为切入口,使学生发现原有比较大小的方法(数方格、直接计算)并不能解决问题,需要寻求新方法来比较大小,激发学生原有经验中的转化体验,让学生开始感悟转化的策略。用“能一眼看出哪个面积大一些”这个问题引导学生去思考,并且让学生说一说这个问题的难度在哪儿,促使学生主动参与学习,寻求解决问题的思路。】
师:老师给每个学习小组准备的信封里都有这样两个图形,请大家看一看、想一想,如果有困难,还可以剪一剪、画一画。
活动要求:
1.在《练习单》上画一画、标一标,表达出你比较的过程。
2.完成后和你的小伙伴分享一下你是怎么比较的?
3.认真倾听其他同学发言,积极反思与自己的想法是否一致?做好分享准备。
●组别:火箭组(共5人)
对应活动内容:阅读例题,讨论如何比较两个面积的大小。
组内角色:小先生1→学生n(小先生主要承担组织、评价职责)
成果共享:汇报交流。
小先生1:老师给我们每个学习小组都准备了一些材料,你们想怎么比较?一起来说说看。
生1:用数格子的方法进行比较。通过这样的方法,我发现两个图形都是48格。
小先生1:这种方法你们觉得怎么样?
生2:我不喜欢这种方法,容易产生误差。
小先生1:那谁有更加准确的方法可以进行比较呢?
生3:我是把左图上面的半圆剪下来,向下平移8格,再把右图两个凸出的半圆剪下来拼到上面,就能得到两个完全一样的长方形。
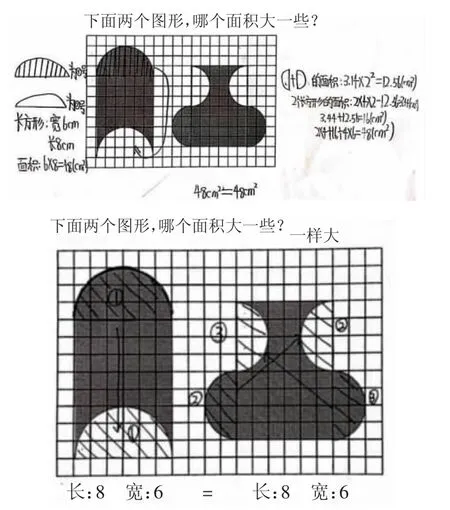
小先生1:如果用剪拼,还有不一样的方法吗?
生4:把左图下面的部分剪下来,向上平移8格,就成为一个长8cm、宽6cm的长方形。把右图左右两边凹进去的部分分别剪下来,拼到下面的两边,得到一个长方形,和左图变化后的长方形的面积相等。
生1:我还想到了一种,把右图沿对称轴剪开翻转,拼成一个同样的长方形。
小先生1:这次给我们提供了剪刀,如果没有这些,可以怎么做?
生3:在《练习单》上表示过程,将去掉的划掉,需要补上的画上去。方法和剪拼的差不多。
小先生1:方法都差不多,就是把这两个图形都转化成了长方形。
师:明明是比较原来这两个图形的面积,为什么要比较后来这两个长方形?
生:原来的图形不规则,难以比较。但是,运用了转化的策略,通过平移、旋转把它们都变成了长方形,就能比较出大小了。
师:这么多种方法都不一样吗?它们之间有什么相同的地方?
生:它们都是把不规则的图形变成长方形。
师:这里的“变”在数学上称为转化。可见解决问题需要找到合适的策略,今天我们重点研究图形中的转化策略。
师:比较转化前后的两个图形,什么变了?什么没变?
生:形状变了,面积没变。
【设计意图:在当前教学环境的背景下,一个班几十名学生,如果忽视个体之间的差异而制定整齐划一的学习目标,实际上难以满足不同层次水平学生的学习需要。在分层的基础上,教师应结合不同层次的学习目标,合理制订各层次学习目标,不同层次的小组根据自己小组的实际情况共同协商选择适合自己小组的学习目标。通过学习,选择哪项学习目标,应掌握到何种程度,并努力去达到选择的目标。学习小组之间的学习方式是多样的:有些学习小组无法直接观察转化,他们可以画出转化的方法,再比一比,也可以在剪拼的过程中逐步体会;甚至有些学习小组进行探索存在困难时,可以在其他小组或者教师的帮助下,先看懂其他小组学员是如何进行操作的,再去尝试,从而体会并得到转化的方法。在整个研究过程中,充分尊重学生,基于已有的知识和经验,有的小组会用数方格的方法,讨论并主动发现数方格的方法并不方便。通过一系列分层的具体活动,将两个复杂的图形转化成简单的长方形,从而得出结果。从数方格比较到转化比较,在不断发现问题、解决问题的过程中,转化的意义逐渐凸显出来。】
二、我会实践-实践中巩固策略
师:刚刚我们研究了不规则图形的面积,下面一起来看看这个实际问题。请在学习小组里讨论。

1.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
●组别:勤奋上进组(共4人)
对应活动内容:尝试解决并讨论如何进行周长的比较。
组内角色:小先生n→学生1(小先生主要承担组织、评价职责)
成果共享:汇报交流。
小先生:谁来说说怎么想的?
生1:将右边图形的边进行平移,平移后就是一个长方形,等于长方形长加宽之和,所以两个图形的周长一样长。
小先生:你们都是这么思考的吗?
组内其他成员表示赞同。
【设计意图:在组内由小先生组织组员进行“练一练”,因为这道题难度较低,且学生已经有了之前练习的经验,所以不难解决。教师通过巡视发现组内这道题基本都已解决,课堂上不再组织统一反馈,符合学生的实际学习需要。】
三、我会回顾-回顾中提升策略
师:看似复杂、不熟悉的问题进行适当地变化,变成较为简单的、比较熟悉的问题的过程,就是转化的策略。对“转化”有感觉了吗?对它有印象吗?很久以前古人就已经运用转化的方法解决问题了,想一想,曹冲是把什么转化成了什么呢?(讨论曹冲称象)
生:把大象的质量转化成石头的质量。
师:其实转化这个策略我们并不陌生,我们曾经用转化的策略解决过哪些数学问题?小组里先讨论看看。
●组别:数学探秘组(共5人)
对应活动内容:回顾相关内容。
组内角色:小先生n→学生n(小先生主要承担组织、评价职责)
成果共享:汇报交流,白板展示。
小先生1:我们好好想一想,说说看。
生1:把异分母分数转化成同分母分数进行计算。
生2:把除数是小数的除法转化成除数是整数的除法。
生3:把平行四边形转化成长方形来计算面积。
生4:三角形和梯形都是转化成平行四边形来研究面积的。
小先生:我们在学习这些内容时,为什么要进行转化呢?
生2:这些知识的学习,都是把未知转化成已知。
小先生:看来我们想的还很多,一起把过程写在白板上吧。
【设计意图:通过引导学生回忆已经学过的内容,将那些零散的知识系统化,使学生认识到解决问题一般要经历化未知为已知的过程,也为学生今后解决问题指出了一个新的方向。真正的学习要有学生思维的参与,比如这里学习小组先进行讨论,得出一定的结论后,为了使其他同伴看清自己的方法,使用了白板这个学习媒介。当他们将过程用文字和图形在白板上展示后,就能看出他们思维的过程。尤其重要的是,教师能看出学生探究过程中出现的问题,以便在接下来的教学过程中做适当调整。】
四、我会练习-练习中提升学力
●组别:快乐数学组(共5人)
对应活动内容:完成相应练习。
组内角色:小先生n→学生n(小先生主要承担组织、评价职责)
成果共享:汇报交流。

1.明明和东东在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
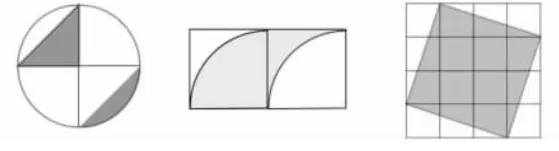
2.用分数表示各图中的涂色部分。
小先生:第一题谁来说说看是怎么想的?
生1:看起来比较复杂,但是如果把右边的两块草坪进行移动,就会发现和右边的图形一样了。

组内其他成员表示赞同。
生2:第二题第一个是四分之一,第二个是二分之一,第三个是十六分之九。
小先生:你们都同意吗?
组员赞同。
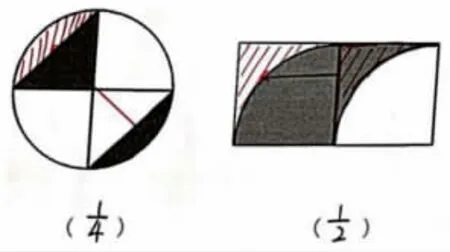
生3:将第三幅图中涂色正方形旋转,正好是9格,因此算出结果是十六分之九。
生4:第三幅图中空白部分的四个直角三角形可以拼成两个面积是3格的长方形,正好是6格,这样涂色部分的面积是10格。所以答案是十六分之十。
生5:第三题我们答案不一样,但是我感觉都是对的啊,这是怎么回事?
小先生:那我们等会就把这个问题提出来问问其他小组吧。
师:刚才大家在小组内交流时遇到了什么困难?
生:其他题目我们都同意,但是最后一题出现了两种答案,我们感觉都是对的。
(学生介绍两种思路)
师:刚才提到了旋转,我们一起看一看课件,旋转后这个正方形是9格吗?a、b两条线段的长度不一样,所以旋转后并不是9格。
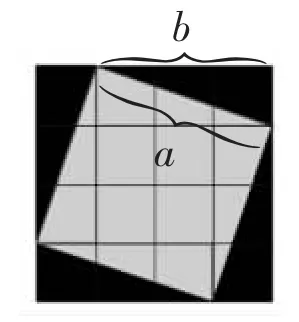
【设计意图:第三个图形相对复杂,更容易激起学生的探究欲望。当学生出现不同想法时,让学生自己说一说、辩一辩,在比较中体会选择合适的转化策略。】
五、全课小结
师:课的尾声老师想和大家分享一句话:天下难事,必作于易;天下大事,必作于细。———老子《道德经》。
