落实“四基”目标 感悟数学思想方法

文|刘占双（特级教师）

《数学课程标准（2011年版）》将“使学生获得数学的基本思想”作为数学课程总目标的“四基”之一，强调了数学思想方法的重要性。数学教学不仅承载着知识、技能的传授，还应该让学生在学习中感悟到知识背后的数学思想方法。在多年的教学实践中，对于如何向学生渗透思想方法，更好落实“四基”目标，我做了一些尝试，现总结如下：

一、巧妙导入，渗透数学思想方法

好的开始是成功的一半。每节课的导入环节，我会结合教学内容创设生动有趣的情境，引导学生发现问题、提出问题，让学生感受到数学有用、有趣。学生在解决问题时，我会顺势而为，启发学生思考解决类似问题时曾经用到的思想方法。

例如，在教学《平行四边形的面积》一课时，创设了“阿凡提买地”的故事情境。阿凡提：“巴依老爷，我想从你这里买一块地，可以吗？”巴依老爷：“当然可以，我这里有两块土地供你挑选，一块土地的形状是长方形，另一块土地的形状是平行四边形，价钱都是1个金币。”

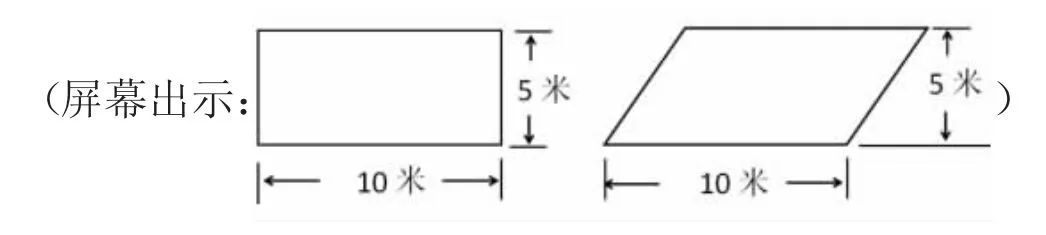
学生根据故事情境提出下面的问题：

1.买哪块土地比较划算？

2.这两块土地的面积各是多少平方米？怎样计算平行四边形土地的面积？

学生的思维被激活，提出了以上几个问题。我顺势而为，高兴地说：“同学们真爱动脑筋，想出了这么多很棒的问题。长方形的面积我们已经学过了，今天我们重点研究平行四边形的面积。如何计算平行四边形的面积？能不能把平行四边形转化成我们学过的图形，再计算它的面积？”

问题提出后，我没有急于让学生马上回答，而是先让学生独立思考，然后同桌讨论交流。学生积极动脑，大胆想象，最后大家一致认为可以把平行四边形转化成长方形，再计算它的面积。

二、巧设活动，感悟数学思想方法

《数学课程标准（2011年版）》明确提出，数学教学是数学活动的教学，让学生在动手实践、自主探究、合作交流中掌握必备的基础知识和基本技能，积累数学经验和思想方法。数学活动既包括学生在课堂上学习数学时的探究性学习活动，也包括与数学课程相联系的学生实践活动；既包括生活中进行的活动，也包括课程教学中特意设计的活动。

“数学的基础知识、基本技能、基本思想、基本活动经验”是一个有机的整体，是互相联系、互相促进的。基础知识和基本技能是数学教学的主要载体，需要花费较多的课堂时间；数学思想则是数学教学的精髓，是统领课堂教学的主线；数学活动是不可或缺的教学形式。在课堂时间的安排上应该有意识地给“数学思想”的教学预留适当的时间，但是“数学思想”的教学不能空洞地进行，一定要以数学知识为载体，并且应该注意将数学知识与数学思想融为一体。

例如，《平行四边形的面积》一课的探究环节。

为了让学生深入探究平行四边形面积的计算方法，进一步感受转化的思想方法，我引导学生利用平行四边形卡纸进行深度学习。

我给学习小组提出如下活动要求：

1.猜：平行四边形的面积可能与什么有关？

2.剪：把平行四边形剪拼成学过的图形。

3.算：算出平行四边形的面积。

4.议：小组讨论平行四边形面积的计算方法。

我给每位学生发放如下学具：平行四边形卡纸、剪刀、透明塑料方格纸等，让学生按照活动要求开展探究活动。

学生通过独立思考、动手实践、合作交流等活动，找到了平行四边形面积的解决办法：可以先把平行四边形转化成学过的长方形，再利用长方形面积的计算方法，算出平行四边形的面积。学生汇报演示之后，教师再利用课件演示平行四边形剪拼成长方形的过程，引导学生进一步理解：平行四边的底边相当于长方形的长，平行四边形的高相当于长方形的宽，平行四边形的面积就是长方形的面积，由于长方形的面积=长×宽，因此，平行四边形的面积=底×高。

通过课堂教学让学生获得活动经验，主要目的是培养学生从数学的角度进行思考，直观地、合情地获得一些结果，并想办法验证自己的猜测。小学数学中基本的活动经验分别是直接的活动经验和间接的活动经验。数学活动经验不仅是操作的经验，还包括学生思维的经验，也就是在数学活动当中思考的经验。学生形成智慧不仅需要掌握基础知识，也需要在活动当中获得经验。因此，我们在课堂教学中要充分挖掘课程资源，尽可能多地让学生在动手操作中经历知识的形成过程，积累数学活动经验，感悟数学思想方法。

三、巧妙练习，强化数学思想方法

数学是思维的体操，通过数学学习，要让学生掌握必备的基础知识，形成技能，还要让学生在思维上有所发展，素养得到提升。因此，在设计课堂练习时，既要考虑设计基础达标练习，还要设计思维提升和感悟思想方法的练习。例如，学习《组合图形的面积》一课后，可以设计如下几个层次练习。

1.基本练习，巩固“双基”的同时感悟数学思想方法。

计算下图的面积。（先分成基本图形，再测量需要的数据，并计算面积）

本节课的教学目标之一是学生会用分割或添补的方法把组合图形转化为学过的图形，并会计算其面积。为了实现上述目标，我设计了上面两道基本练习。

2.变式练习，提升思维的同时感悟数学思想方法。

用不同的方法计算下面图形的面积。（教师为每位学生准备了用卡纸做成的如下图形）

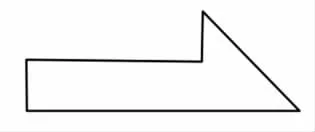
活动要求：

（1）想一想、画一画。想办法把上图转化成学过的图形，在图中画上分割线。

（2）剪一剪、看一看。沿着分割线剪开，看看转化成了哪些基本图形。

（3）量一量、算一算。量出需要的数据，计算图形的面积。

让学生用不同的方法计算组合图形的面积，旨在培养学生思维的灵活性和开放性，让不同层次的学生都能在原有水平上得到发展，学生感受到解决问题策略的多样性，同时感悟到转化的思想方法在解决问题时发挥的重要作用。

四、总结提升，深化数学思想方法

思想方法的感悟，既要体现在知识形成、发展和应用的过程中，又有赖于学生自觉地进行回顾和反思。在教学中也应有意识地组织学生开展回顾和反思活动，引发学生对所学知识进行更深刻的思考：遇到新问题时，我们是怎样解决的？你积累了哪些成功经验？引导学生看到具体活动过程背后的思想方法，体会思想方法的引领作用。

例如，《组合图形的面积》一课，学生经过自主探究、合作交流和汇报展示后，绝大多数学生对组合图形面积的计算方法已初步理解，但仍有少数学生对“转化”的方法印象不深，所以教师还要引导学生进行回顾反思，并利用课件演示组合图形转化成基本图形的过程，使学生进一步理解“转化”的思想方法。

再如，教学《异分母分数加减法》，下课前我会引导学生回顾反思：“计算异分母分数加减法有哪些策略？画图、通分、化小数这几种方法有什么相同的地方？”使学生能够整体地认识到这些方法都运用了“转化”的思想，把新知转化成了旧识，深刻感悟知识背后的思想方法。

实践证明，让学生掌握基本的数学思想方法能使数学更易于理解，领悟数学思想方法更有助于学生新知的学习，提高学生分析问题和解决问题的能力。