基于前测分析 寻找贴合学生的有效学习路径

王优琴

摘 要：数学教师要充分了解学生的认知发展水平和已有的知识经验，对其进行客观的分析，设计开展有效的教学实践。主要通过对“直角”这一概念的前测统计与分析，发现学生学习直角这一知识的难点、困惑点，教师通过利用丰富学材、多元联动、空间想象等方法寻找贴合学生的学习路径，有效地促进学生对直角概念的认知。

关键词：前测分析;学习路径;多元联动

一、课前思考：“认识直角”一课的重要性

古文云：“离娄之明，公输子之巧，不以规矩不能成方圆。”这里的矩是指曲尺：一直一横成直角的尺，是木匠打制方形门窗桌凳必备的角尺。可见在战国时期，人们已经认识并用到了直角。

直角是构成生活中许多特殊图形的基本要素，在认识直角之前，学生对于三角形与四边形的构成要素（边、角、顶点）已经有所认知，但尚未进一步察觉其角度的特殊性，在引出直角概念之后，学生对这些图形的构成要素有了更进一步的认识：直角三角形有一个直角，长方形、正方形有四个直角，生活中，很多物体表面都有直角。学习直角既是实际生活的需要，又是学习后续知识的基础：比直角小的角称为锐角，比直角大的角称为钝角，此时的直角具有了工具性的作用，它被作为一个标准、一种参照物区分锐角与钝角，同时对于直角特点的认识也是学习垂直的基础，平面上两条直线的垂直关系的引出与直角息息相关。

小学阶段对于直角的研究主要经历三个阶段。一是定性研究阶段。这是直角概念的启蒙阶段，这一阶段对于直角仅是初步认识，学生能描述像三角尺上的这样的角就是直角即可。二是定量研究阶段。这一阶段，学生对直角的认识由质向量过渡，对于直角的认识再不仅仅停留在表象阶段，而且要从量的角度对直角进行定义：90°角是直角。三是同一平面内两直线特殊位置关系阶段。当两条直线相交成直角时，这两条直线互相垂直，在这一阶段学生以交角是否是直角来衡量平面中两条直线的位置关系。

二、学习前测，探底学生心中的直角

课前，我以问卷调查的方法对城区两个班级80个学生进行了前测调查，探底学生心中的直角，了解学生的认知基础和起点水平，以期更好地展开教学。

（一）你听说过直角吗？

直角这一名称对于学生来说并不陌生，“直角转弯”“直角尺”等在学生的生活学习中经常被提及，因此有92.3%的学生都听说过直角。

（二）判一判，是直角的请打“√”。

（三）你觉得下边的三角尺上有直角吗？（如果有，请你描一描。）

找三角尺上的直角对于学生来说有一定难度，64.1%的学生无法正确找到两把尺子上的直角，如果将这两把尺子斜放置，如：，能正确找到直角的学生更是寥寥无几。

（四）你觉得一副三角尺上的兩个直角，它们一样大吗？

学生一致认为不同的直角，边的长短不同，开口方向不同，所以直角的大小也是不一样的。

三、基于前测分析，寻找贴合学生的有效学习路径

有效的学习路径并不是指最特别的教学方法或者手段，而是教师根据不同学生设计的最适合他们的教学方案。从前测的数据分析来看，学生对于直角的认识仅停留在放“正”的直角，他们对直角的判定容易受到开口方向、边的长短等非本质因素的影响。为了构建完整的直角概念，丰富直角表象，凸显直角的本质特征，教师通过丰富学材、多元联动、空间想象、凸显关系等教学方法，让学生经历直角概念的形成过程。

（一）丰富学材，完整建立直角概念

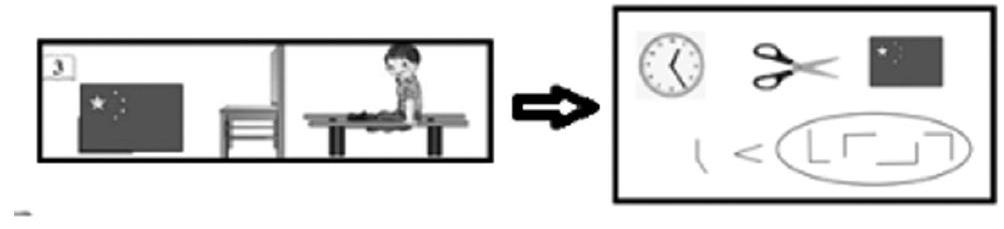
为了让学生体会直角是一类特殊的角，直角有着所有角的构成特点，但又有其特殊性——大小相等，建议教师舍弃教科书中的椅子和双杠两幅图，增加两个反例实物图：钟面和剪刀，然后从学生熟悉的国旗图里直接引出不同方向的四个直角，初步建立直角表象。这样的处理——从三类角中提取出直角作为本节课的研究对象，使“直角”这一新概念在学生已有的认知结构中找到一个最佳的“生长点”，有利于让学生了解角与直角的关系，体会直角是一类特殊的角。

（二）多元联动，丰富直角表象

建立直角表象，感知直角的本质特征，是本节课的教学重点，也是学生学习的难点。学生对于直角的认识仅停留在放“正”的直角，他们仅接受一边是水平，另一边呈铅直情况的直角，倾斜摆置的直角不被认可。针对这一学情，教师设计了有效的操作活动，利用多元联动，丰富直角表象，构建完整的直角概念。

1.叠一叠，比一比，揭示直角本质特征

三角尺上的直角对学生来说是最熟悉的，虽然说有一部分学生能正确找出三角尺上的直角，但是对于直角的本质特征：大小相同，学生并不接受。为了突破这一思维定式，教师安排了多个操作活动：（1）找一找，老师手中一副大三角尺上的两个直角，比一比这两个直角的大小。（2）同桌互相找一找手中的一副小三角尺上的直角，比一比这两个直角的大小。（3）比一比老师大尺子上的直角和学生小尺子上的直角的大小。（4）猜一猜全国各地小朋友手中三角尺上的直角是否一样大？直角是一把“标尺”，是衡量锐角和钝角的依据。教师从学生最熟悉的三角尺上的直角入手，通过找三角尺上的直角，并通过多次比较、多次重叠，促使经验不断累积，让体验更趋丰盈，用实践揭示直角的本质特征，明确所有的直角大小相同。

2.转一转，指一指，丰富直角表象

从前测发现学生对于直角的表象只停留在“直的”“方方的”“一横一竖的”，为了丰富直角表象，教师设计了不断转动三角尺，让学生找不同开口方向的直角的活动，逐步丰富学生的直角表象。

【课堂回顾一】

师：看，老师手里有一把三角尺，你能找到尺子上的直角，用手势比划出来吗？

师：尺子转了起来，你还能找到直角吗？

在初步感悟实物图中的直角后，教师充分利用三角尺，引发学生对三角尺上的直角的关注，让学生寻找三角尺上的直角，然后转动三角尺，继续让学生寻找放置方式不同的三角尺上的直角，从而揭示出直角的概念，初步感悟直角变式图，建立丰满的直角表象。

【课堂回顾二】

（活动一：不断旋转直角，请学生判断转动后是不是直角）

（活动二：拉动直角的两条边，再次判断是否还是直角）

教师将两次操作活动后的直角搬迁出来，并质疑学生：第一次变出来的三个角都是直角，第二次却不是了，为什么？学生交流释疑：直角旋转后，虽然开口方向变了，但是它的大小没变，但如果拉动直角两边，就改变了角的大小，它就不是直角了。通过这一操作活动，既丰富了直角表象，同时又凸显了直角的本质特征：直角都一样大。

3.看一看，辩一辩，加深直角本质认识

能正确判断斜放的直角是本节课的教学难点。初步认识了直角后，教师安排一道判断直角的练习题（如下图），以学习单的形式，先独立判断，然后寻找相同点和不同点。对于直角的判断，教师应该让学生自由发表意见，然后通过辩论交流，统一明确验证方法：借助三角尺中的直角进行比对，通过观察是否完全重合来确定是否是直角，让学生感受到用三角尺比一比的需要，加深对直角本质的认识。

4.找一找，创一创，深化直角概念

空间观念的形成不像拍照，想建立空间表象、几何模型，必须有“动手”的过程。在学生初步认识了直角后，教师安排找一找身边的直角，并通过摆一摆、拼一拼、折一折、画一画等创造直角活动，学生在“找”“拼”“搭”“折”“画”自由多样的操作活动中加深对直角的认识，获得深刻的体验，这不仅是动手实践的过程，更是尝试、想象、推理、验证、反思的过程。

（三）空间想象，突破定势，凸显关系特征

在学习本节课之前很多学生对于直角的认识往往都停留在直角是长方形（正方形、三角形）的一部分，为了凸显直角其实是两线之间的一种特殊的位置关系，为垂直与平行服务，在练习环节安排了以下数直角练习。

【课堂回顾三】

师：你觉得老师画的是直角吗？（电脑验证后延长直角的两条边）现在你能找到几个直角呢？（生上台指直角）

师：现在有几个直角了呢？

生：8个。（上台指一指）

平面上两条直线的垂直关系的引出与直角息息相关，直角的学习最终是为垂直服务，在此之前，學生从来不会想到关注直角的两条边，一直将直角作为长方形、三角形的一部分来进行判断，为了打破这一思维，教师将直角的两条边慢慢反向延长，呈现两条相交的直线，再请学生判断有几个直角，最后完整呈现正方形图，学生找齐图中的8个直角。这样的安排，更加有利于学生对于两条直线的位置关系的关注，为学习垂直做准备。

参考文献：

卡尔·B.数学史[M].秦传安，译.北京：中央编译出版社，2012.