小学课堂教学中渗透数形结合数学思想的方法

桑青卓玛

【摘要】众所周知，数学始终是小学课程的重要组成部分，是研究自然科学的重要基础，在小学教学活动中扮演着十分重要的角色，数形结合能将抽象问题直观化、复杂问题简单化、隐形问题形象化，有利于激发学生学习数学的兴趣和提升数学教学的效率。对于小学教师而言，如何渗透数学结合的思想，发挥数形结合的优势，帮助同学们更好的学习数学知识成为本文研究的课题。

【关键词】小学数学;渗透教学;数形结合

1. 数形结合思想的教育价值

著名数学家华罗庚曾说：“数与形是相辅相依，永不分离的。”所谓数形结合思想，即是利用形象直观的空间形式将抽象的数学理论和数量关系展现出来，按照“数”与“形”的对应关系，充分发挥两者的优点，利用两者的相互转化来解决实际的数学问题[2]。总而言之，数形结合这一数学思想，可以将复杂问题简单化和抽象问题具体化，促使学生突破问题表述和形式的束缚，深刻理解数学问题的核心要义，实现了抽象思维与形象思维的充分融合，有利于培养和提升学生的思维能力和观察能力，不断增强学生的数学思维意识，为未来的数学学习奠定坚实的基础。

数形结合思想在小学尤其是中高年级的数学教学中具有很大的教育价值，小学生正处于心智发展的关键时期，准确理解和掌握数学教材中的全部数学理论和知识是很困难的，积极将数形结合思想应用于小学数学教学工作中，有利于改善“一言堂”單调枯燥的教学模式，促使学生亲身经历数学活动的过程，与此同时，学生正确理解问题是解决问题的关键，“数”与“形”之间的正确转化，为数学问题的解决提供了新的思维方式，当数学问题的数量关系较为复杂时，利用“形”的方式可以使问题迎刃而解。

2. 数形结合思想的教育优势

（1）抽象问题直观化

“分数”存在着一定的抽象性，小学生在理解分数问题时往往弄不清楚分数表示什么，很多同学无法比较分数的大小，这就对后续分数计算等问题直接造成影响。而数形结合可以将抽象问题直观化，使得小学生对“分数”这个数学问题有直观的认识，变得不再惧怕数学，乐于学习数学，也能学好数学，为后续学习打下良好基础。

（2）复杂问题简单化

小学生在学习时常常对已知条件较为复杂的题很抵触，无法找出已知条件中的各个变量，不能理顺清楚各个已知条件变量之间的关系，导致求解困难，进而感觉数学学起来困难有抵触情绪。对于这类问题，应用数形结合的思想，将复杂的问题简单化，使得已知条件清晰明了的展现在眼前，学生学习时会很清晰，解题时也很容易很多。

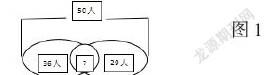
案例2：班级有50名同学，午休时间同学们买零食，其中喜欢吃糖饼的同学有36人，喜欢吃豆干的同学有29人，问同时喜欢吃糖饼和豆干的同学有多少人？

解题过程中借助数形结合的思想，利用韦恩图表示相互包含的关系，让学生瞬间抓住题中已知条件，在脑中形成数量关系网图，通过图像回忆所学知识，找寻已知条件之间的关系，将复杂的问题简单化，轻松解题。

（3）隐形问题形象化

方程教学始终是小学教学中的重点和难点，也是未来数学学习的重要基础。在实际的教学工作中，学生对未接触过的隐形问题有想象的困难，所以，教师必须要采用数形结合的教学方式引导学生准确掌握列方程的方法，这样才能有效的利用方程解决实际问题。

案例2：在教师节来临之际，校园内掀起了送贺卡的活动，已知李老师和王老师共收到贺卡7张，其中王老师收到贺卡3张，请利用列方程的方式求李老师收到贺卡多少张？

首先，可以假设李老师收到X张贺卡，列出以下方程：

X+4=7即是解决此题需要列出的方程，加深了学生对“字母表示数”这一概念的理解，本题中将“隐形”参数X形象化为教师的贺卡，并且展现在同学们的眼前，这样绝大部分学生都能够准确理解这一方程的意义，并且能够顺利解决这一问题，显著提升了解题效率。

3.小学课堂教学中渗透数形结合的数学思想的方法

2011年颁布的《义务教育数学课程标准（最新版）》中明确指出数学课程改革的总体目标：“获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”对于小学教师而言，新课程改革打破了多年来形成的课堂教学重视双基的传统，面临这种改革，教师既要转变教学观念，又要提升教学素养。教师在小学课堂中渗透数形结合的数学思想，主要通过以下形式：

（1）图形感知理解渗透法

德国哲学家康德认为“缺乏概念的直观是空虚的，缺乏直观的概念是盲目的。”因此结合低段小学生的年龄特点，以“图形直观”的形象思维代替数学计算教学中的抽象思维，更好地形成数学语言的直观表象性，利用图形将数学抽象概念转化为看的见的数学知识，使学生更好的理解和掌握数学概念。教师在课堂中可以画出图形，如图1所示。然后一个一个抹去图形中的圆圈来让学 生们充分理解减法的意义。

（2）动手操作理解渗透法

数形结合教学方法在小学低段数学教学的有效运用，提升学生的计算能力，引导学生在“感知——表象——概括”的过程中动手操作，在体验中感知数学规律，调动学生的感观，在大量直观形象的事物中获得感性知识和积极探索的习惯，理解算理，并自己总结出算法。当学生养成良好的画图习惯后，就会在解决数学问题的时候自然而然地结合图形分析问题，促成幼儿的动手能力以及独立思考和解决问题的能力。如设计长方形花辅，长10米，划去一个最大的正方形后，在剩余的花圃的四周围上篱笆，这个篱笆应该多长。通过画图可以使这个问题变得一目了然，学生在动手操作中也可以更加轻松地解决这个问题。可以让同学们用绳子动手操作起来，自己加深对题目的理解，进而学会数学方法的运用。

总之，数形结合思想，以小学数学教学阶段的认知程度上可理解为对数学问题的一种解决思维方式方法。对于数形结合数学思想的教学渗透，能够帮助小学生对小学数学知识有结构性的理解，同时也能够提升他们学习数学的独立性能力与整体学习效果，并有效解决生活中数学问题。

参考文献

[1]崔娜娜. 小学低年级数学教学中数形结合思想的渗透[J]. 中外交流，2021，28（4）：1386.

[2]庄美良. 小学数学教学中数形结合思想的渗透研究[J]. 科普童话·新课堂（上），2021（12）：60.