一些特殊图的剖分图的能量

张海东

(兰州交通大学数理学院 甘肃 兰州 730070)

0 引言

本文考虑的图均为简单无向连通图。设图G的顶点集为V(G)={v1,v2,…,vn}，边集为E(G)={e1,e2,…,en}。若图G中两个顶点vi与vj相邻，则记为vivj，并用di表示顶点vi的度，也即是与vi相邻顶点的数目。设图G的邻接矩阵为A(G)=(aij)n×n，其中当vivj∈E(G)时，aij=1；否则aij=0。

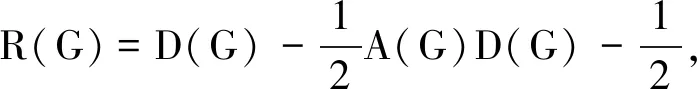
记图G的关联矩阵为B(G)=(bij)n×m，其中

并将B(G)的转置记为B(G)T，易得图G的规范的无符号拉普拉斯矩阵Q(G)满足[5]

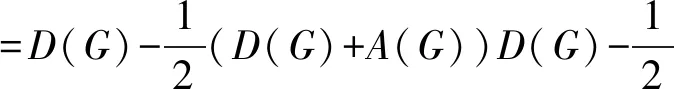
=In(G)+R(G)

(1)

其中In为n阶的单位矩阵。

剖分图S(G)是在图G的每条边插入一个新顶点所得到的图。显然，S(G)是一个二部图，因此，V(S(G))=V1∪V(G)，其中V1是新插入的度为2的顶点集。

1 主要结果

定义1[6]友谊图Fn是将3长圈C3的n次复制收缩在一个公共顶点所得(如图1)，其中n是任意正整数。显然，Fn的顶点数和边数分别为2n+1和3n。

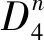
图1 友谊图

图2 荷兰风车图

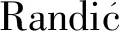
RP(Km,n,λ)=λm+n-2(λ2-1)

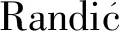
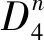
引理5[7]若M是一个非奇异方阵，则

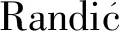
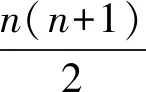
则

R(S(Kn))

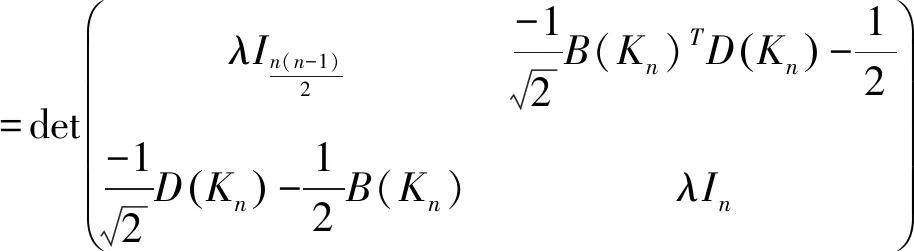
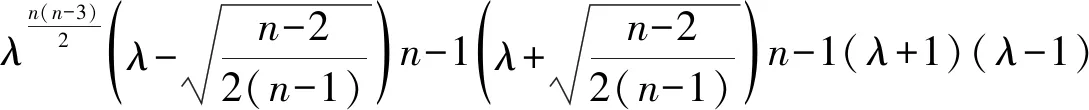
证明易知S(Km,n)的顶点数为mn+m+n，并且S(Km,n)的度对角矩阵D(S(Km,n))和邻接矩阵A(S(Km,n))分别为

则

R(S(Km,n))

det(λImn+m+n-R(S(Km,n)))

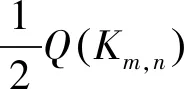
det(λImn+m+n-R(S(Km,n)))

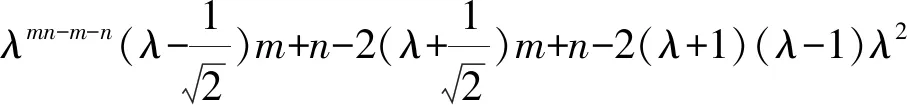
证明易知S(Fn)的顶点数为5n+1，并且S(Fn)的度对角矩阵D(S(Fn))和邻接矩阵A(S(Fn))分别为

则

R(S(Fn))

det(λI5n+1-R(S(Fn)))

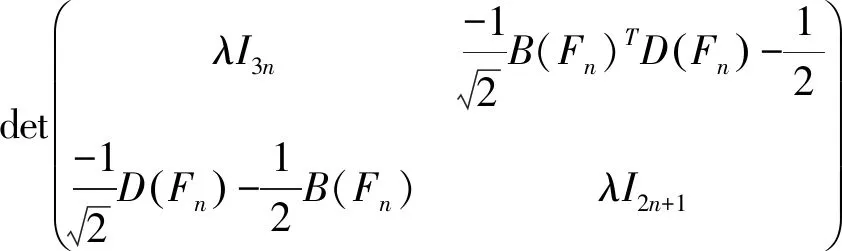
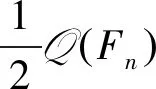
det(λI5n+1-R(S(Fn)))

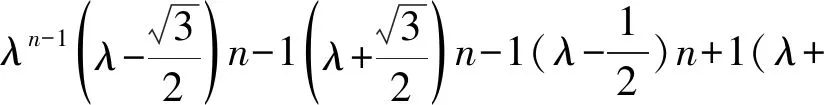
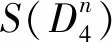
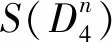
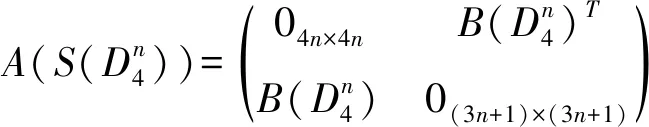
则

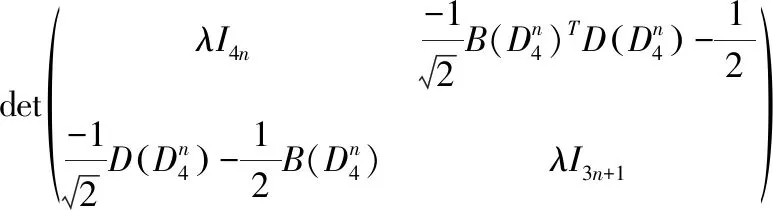
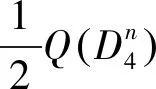
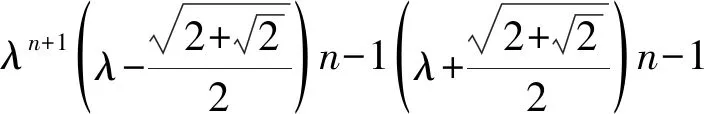
2 结语