开发具有可重构结构的运输机器人

М Ю Рачков，武 确

(莫斯科理工大学 俄罗斯 莫斯科 107023)

在紧急情况下，例如火灾，以及在对人类有害的操作(如排雷)中，有必要以自动方式将适当的技术检查或救援设备运送到工作区域。而解决此问题的简便方法就是使用带有指定设备的运输机器人。

考虑到在现实工作中会经常在非结构化环境中工作的特殊性，所以制定了开发自动运输机器人的方案[1,2]。如果在紧急情况下使用带有安装车载设备平台的履带式运输机器人[3]，那么这些机器人就需具有在未知环境条件下能自由移动，且在平坦路面上能高速运动的能力，但是由于缺少轮子，它们不仅在平坦表面上的移动速度会降低，而且当它们遇到与自身高度相当的障碍物，或遇到楼梯状障碍物的时候会无法越过障碍物。

根据所遇到的问题，经过精心设计加了轮子后的机器人通过模拟仿真得出可以在各种类型的表面上移动，包括在城市环境中需要克服的复杂障碍(例如阶梯楼梯)；该机器人在平坦表面上的移动速度超过了仅装有履带式螺旋桨车辆的移动速度[4]，而且使用寿命将会更长(因为履带在沥青或混凝土等坚硬表面上行驶时会有磨损)。该机器人应用范围广，不仅可以在崎岖不平的地形上移动，而且能克服各种形状的障碍物，包括那些高度大于自身高度的障碍物[5]。

1 运输机器人的构造

机器人的设计建议包含一个组合的推进系统，该系统包括可变换的履带和车轮组(如图1)。

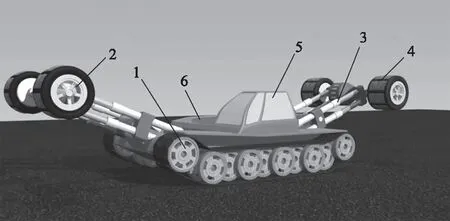
图1 运输机器人注：1-履带组；2-轮组;3-伸缩杆；4-延伸部分(长钉)；5-车载控制系统；6-技术平台

该机器人在技术平台的侧面有两个履带驱动器，在履带组之间的平台前面和后面各安装了两个车轮驱动器[6]。其独特之处在于，车轮驱动器的颈轴通过杠杆与平台连接，杠杆驱动器放置在平台上，可以使车轮驱动器相对于平台垂直移动。伸缩杆的长度可以变化，这使得机器人可以克服各种障碍。而且，车轮上还有一些延伸部分，可以用荆棘(长钉状)的形式制成。该解决方案增加了车轮的直径并提高其越野能力。

已经在SolidWorks软件中创建了机器人的运动学模型来研究其运动的各种模式。通过带有可伸缩元件且带有履带组升高的轮组在平坦表面上移动，这样可以提高机器人的移动速度(图2a)。

在不平坦表面上的运动仅由履带组执行(图2b)，车轮驱动器在此模式下升高，以提高通行性。

可以通过同时使用车轮和履带组来克服复杂几何形状的楼梯和障碍物，在这种情况下，车轮组相对于履带组的位置角度、杠杆的长度以及车轮轴颈的延伸高度则取决于楼梯和障碍物的大小和形状(如图2c、2d)。根据运动学仿真的结果显示，该机器人具有克服各种障碍的能力。

图2 机器人在各种类型表面上的运动模式注：a)平坦的表面；b)凹凸不平的表面；c)楼梯；d)复杂几何形状的障碍物

2 机器人控制系统

机器人控制系统可以根据道路和障碍物的特征自动重新配置履带和车轮的位置，这些特征取决于障碍物的高度、障碍物的宽度、平台倾斜角度、到障碍物的距离以及是否存在下一个上下台阶等数据[7]。图3显示了机器人控制系统的框架。

控制对象是带有技术设备的机器人平台[8]。履带和车轮速度控制单元根据操作员的命令以编程方式或远程方式设置相应速度的值。测量和转换单

元使用传感器收集有关外部条件的信息，将其转换并传输到操纵器和峰值控制单元，并根据此信息重新配置机器人的参数，即可控制伸缩杆的倾斜和伸展以及轴颈的长度。跟踪测量单元的结构如图4。

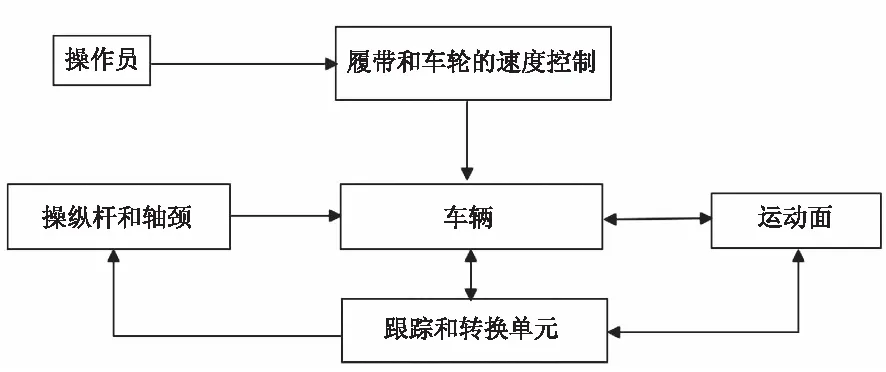
图3 机器人控制系统

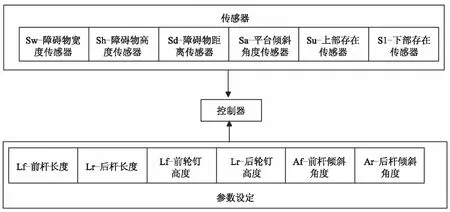
图4 跟踪测量单元

微控制器从传感器接收到有关位置和障碍物的信息后，发出信号以更改设计参数的配置，即杠杆的长度，倾斜角度以及轴颈的高度。当机器人移动时，从传感器接收到的当前信息会发生改变，随之微控制器根据该信息产生相应的控制信号传输给驱动系统。

3 机器人的实验模型

机器人的实验模型是该机器人的微型复制品，它是根据标准组件制成的，即带有内置驱动器的车轮组和履带组，它由遥控器控制。实验模型的一般视图,如图5所示。

图5 实验模型的一般视图

如图5所示，模型的总体尺寸为：长500 mm，宽250 mm，高170 mm。当车轮组移动时，机器人的长度和高度也会随之改变。

在机器人的实验模型中，每个轨道的驱动控制单元都包含一个由变频器控制的异步电动机。速度反馈由电机轴上的测速发电机来完成。来自测速发电机的信号被馈送到ADC输入，然后以数字形式被馈送到基于比较设备和数字控制器构建的轨道速度控制单元。在该系统中使用调节器可以补偿与电机轴上力矩变化相关的运动速度变化。随着扭矩增加，转速降低，调速器调节控制信号以保持速度恒定，同时控制电动机的最大交流频率。

杠杆由具有电动机过载和短路保护功能的直流电动机驱动。为了确定臂的倾斜角度，使用了来自光学传感器的信号，这些信号通过ADC转换为数字形式。用于确定所需控制信号的算法在用于计算倾斜角度和杠杆长度的程序中实现。

工作能力结构的可操作性通过无线电频道上的远程手动控制进行了测试。测试表明，该机器人可以执行所有运动模式，包括沿着楼梯上下运动。

4 用于杠杆延伸控制的执行器的仿真

为了分析控制单元的操作，以使用全尺寸机器人的参数扩展控制杆，在Matlab应用程序中的Simulink中使用相应的标准模块进行了仿真。杠杆扩展控制的仿真方案,如图6所示。

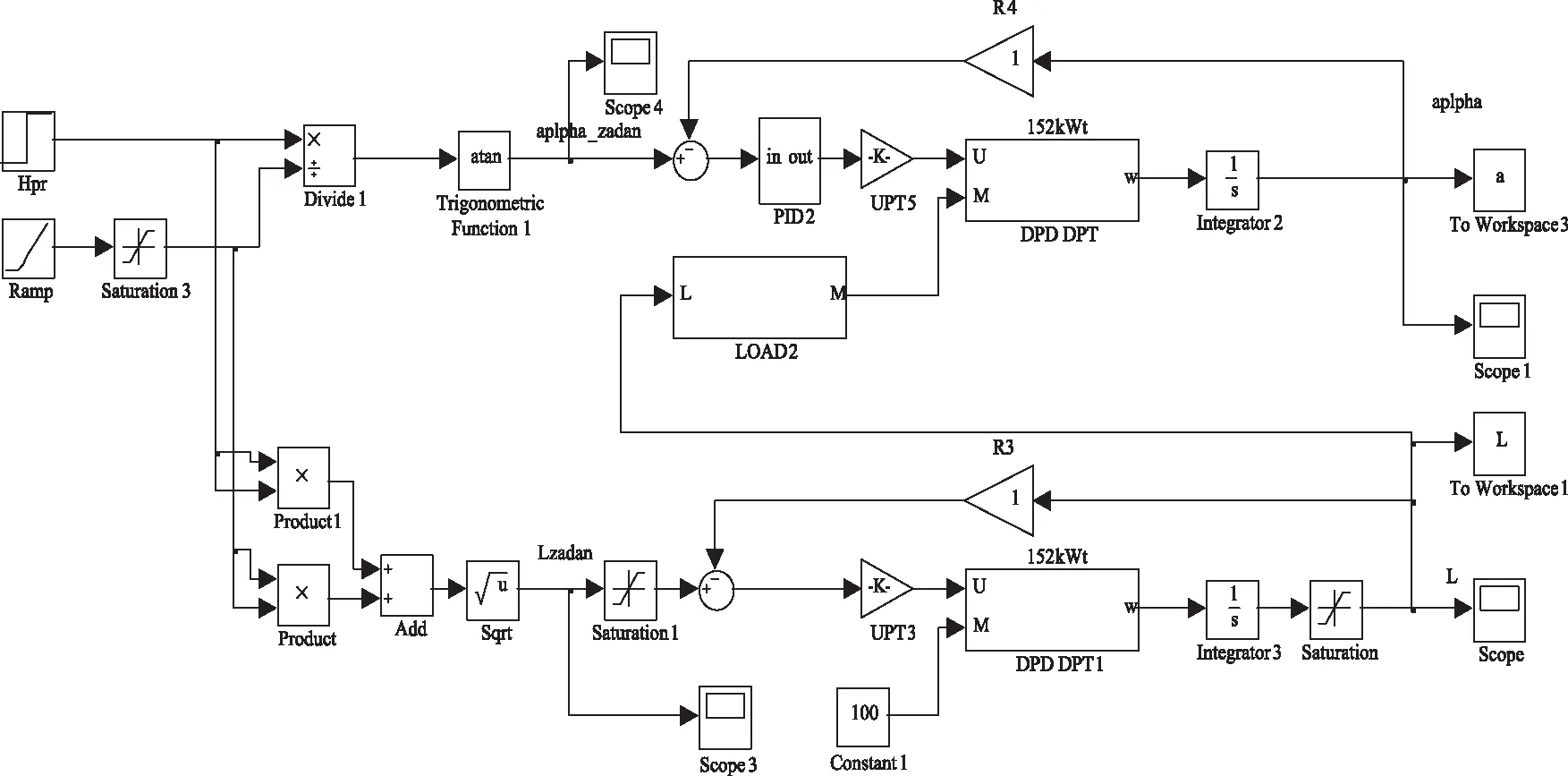
图6 杠杆扩展控制的仿真方案

用于计算杠杆角度和长度的输入控制参数是障碍物的高度和到障碍物的距离(如图7所示)。

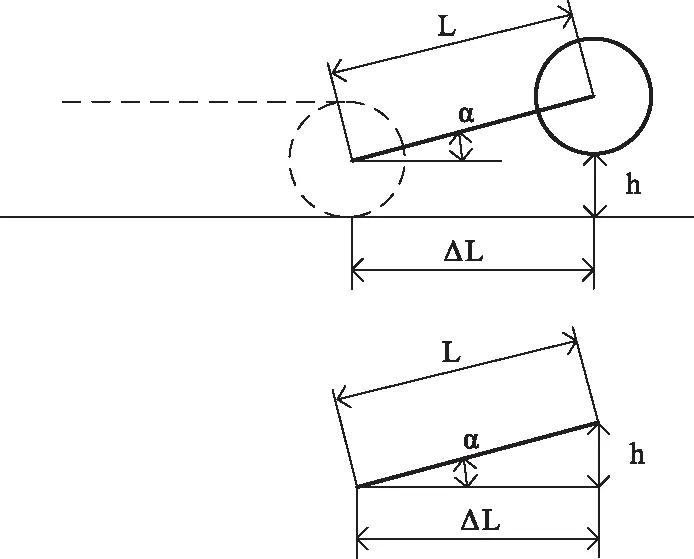
图7 计算杠杆长度和倾斜角度 注：L为杠杆的长度；h为障碍物的高度；ΔL为到障碍物的距离；α为杠杆的倾斜角度

根据计算方案，设置杠杆长度的公式为

其中L是杠杆的长度；h是障碍物的高度；ΔL是到障碍物的距离。

计算杠杆倾斜角度的公式为

其中，α是杠杆的倾斜角度。

在杠杆角度控制回路中使用典型模块，特别是标准PID控制器。在对操纵杆控制模块进行建模时，以阶梯函数的形式设置障碍物的高度。到障碍物的距离是使用与接近障碍物相对应的斜坡模块通过线性函数设置的。由于此值不能为负，因此通过使用Saturation3模块将距离限制下限设置为零。使用Divide1和Trigonometric Function1模块计算杠杆的倾斜角度。杠杆长度是使用Product、Add和Sqrt模块计算的。饱和模块位于控制信号计算模块之后。它将这些信号限制为最大允许值。例如，杠杆的长度不能超过1.5 m，并且角度限制为90°。杠杆长度驱动器上的负载被认为是恒定的，并由一个常数给出。杠杆角驱动器上的负载定义为作用在杠杆上的机器人的重力。考虑使用瞬态过程来研究Simulink程序包中的已开发模型[9]。以下是对杠杆长度稳定性的研究结果，其输入参数是到障碍物的距离，输出参数是杠杆的长度。

图8显示了杠杆长度控制单元的瞬态响应。从图中可以看出，其形状对应于非周期性过程，因此系统是稳定的，因为图线趋于达到稳态值(在这种情况下为1)。 图上没有过冲和振荡过程，调节时间约为0.3 s。

在脉冲响应(图9)上，可以看到其收敛到零的过程，这也表明其系统的稳定性。

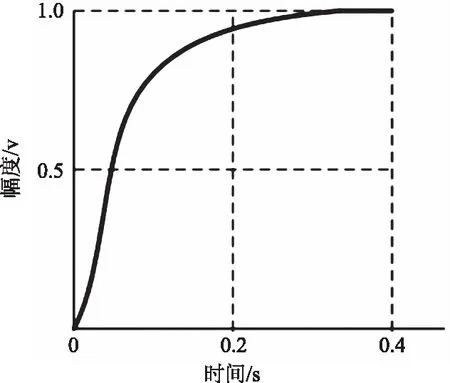
图8 杠杆长度控制单元的瞬态响应

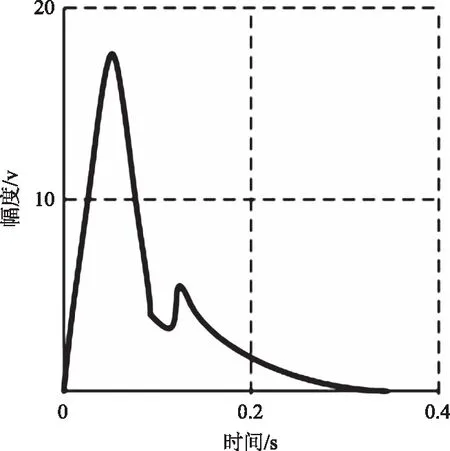
图9 杠杆长度控制单元的脉冲响应

根据对相频(PFC)和幅频特性(AFC)的研究结果(图10)，可以得出结论，系统是稳定的，因为幅频特性(AFC)在0值以下。

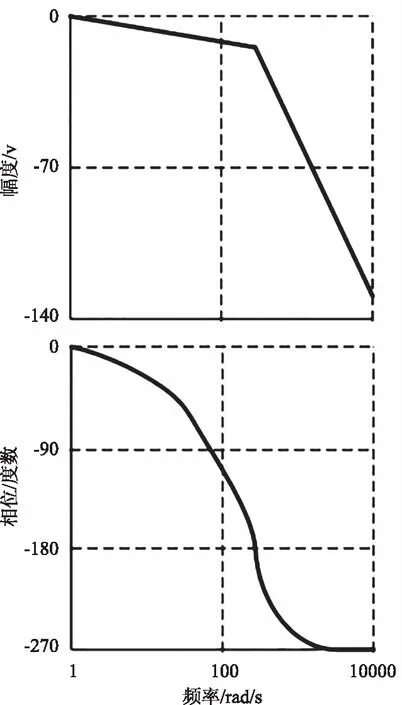
图10 幅度频率响应图(上)和相位频率响应图(下)

因此，满足了稳定性条件，因为频率响应曲线比相位响应曲线穿过180°线的时间早于零值。幅度稳定性裕量由AFC图确定为在PFC图与180°线相交的频率下到OX轴的距离。在这种情况下，稳定裕度为12.9 dB。

另外，系统的稳定性通过奈奎斯特准则进行了检验(如图11所示)。

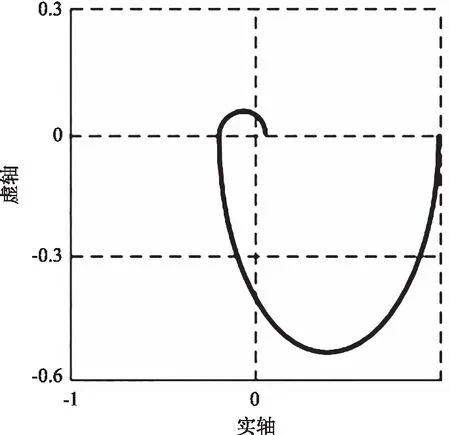
图11 奈奎斯特曲线分析图

在这种情况下，稳定性条件是曲线图不应覆盖坐标为(-1，i0)的点。从获得的结果可以看出，该条件已得到满足。因此，此系统是稳定的。图上标记的点对应于0°和180°线的频率响应和相位响应的交点。

因此，对杠杆长度驱动器控制系统的仿真，根据各种标准已证实了其稳定性。

5 结论

开发了一种运输机器人的新方案，该方案可以实现在高风险区域以及人类难以到达的地方执行各种类型的工作。机器人的自动控制系统设计可以根据移动表面的类型和由测量单元确定的障碍物的大小来重新配置其结构。

为研究机器人的不同运动模式，我们在Solid-Works软件中创建了机器人的运动模型。且基于标准组件的远程控制机器人的实验原型也已创建。在实验室的测试中也证实了可以克服各种障碍的能力。并且通过在Matlab Simulink程序中对杠杆伸展控制系统进行了仿真，也显示了给定参数下系统的稳定性。结果显示可用于创建全尺寸实体机器人。