全国名校数列综合拔高卷（B卷）答案与提示

一、选择题

1.C 2.C 3.C 4.A 5.C 6.B 7.D 8.D 9.B 10.A 11.D 12.B 13.D 14.C 15.C 16.B 17.B 18.A 19.D 20.D 21.C 22.B 23.B 24.B 25.A 26.A 27.C 28.D 29.C 30.D 31.C 32.B 33.C 34.C 35.C 36.D 37.A 38.D 39.B 40.A

二、填空题

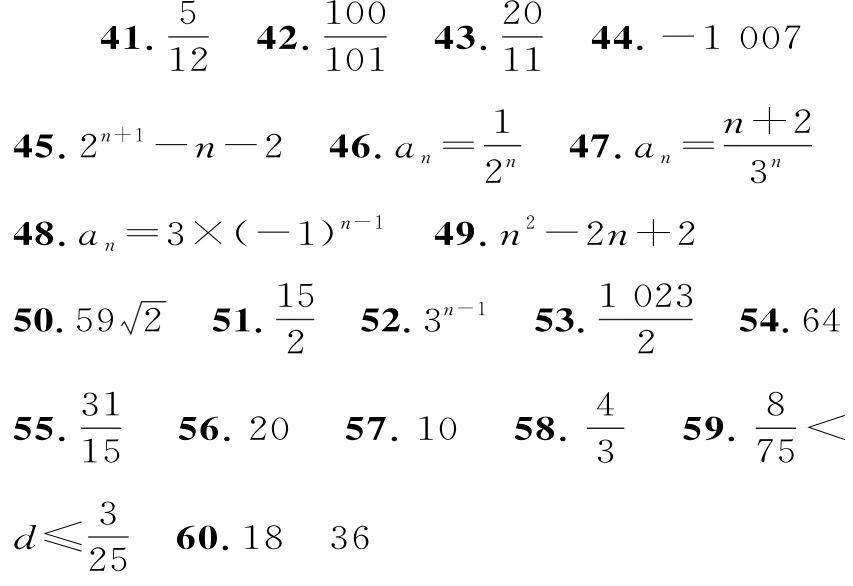
得,log2（a1a2a3）=15,所以a1a2a3=215。

设等比数列{an}的公比为q,因为a1=8,所以an=8qn-1。

因此,8·8q·8q2=215,解得q=4。

所以an=8·4n-1,an=22n+1。

（2）由（1）得bn=2n+1,易知{bn}为等差数列,Sn=3+5+…+（2n+1）=n2+2n。

三、解答题

61.（1）由bn=log2an和b1+b2+b3=15

由a1,12a5,2a3成等差数列,得a1+2a3

63.（1）由a2n-2nan-（2n+1）=0得[an-（2n+1）]· （an+1）=0,所 以an=2n+1或an=-1。

又数列{an}的各项均为正数,所以an=2n+1。

（2）由 （1）知bn= （-1）n-1·an=（-1）n-1·（2n+1）。

所以Tn=3-5+7-9+…+（-1）n-1·（2n+1）。①

可知-Tn=-3+5-7+9+…+（-1）n-1·（2n-1）+（-1）n·（2n+1）。②

①-②得,2Tn=3-2[1-1+1-1+…+（-1）n-2]-（-1）n·（2n+1）=3-2×（-1）n-1（2n+2）。

所以Tn=1+（-1）n-1（n+1）。

64.（1）因为数列{an}满足a1=2,an+1-an=2n-1（n∈N*）,所以a2-a1=20,a3-a2=21,a4-a3=22,…,an-an-1=2n-2（n≥2）。

把以上n-1个式子相加得,an-a1=20+21+…+2n-2（n≥2）。

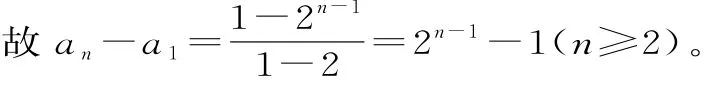
又a1=2,所以an=2n-1+1（n≥2）。

a1=2也满足式子an=2n-1+1,所以an=2n-1+1（n∈N*）。

当n=1时,a1=S1=1;

当n≥2时,an=Sn-Sn-1=（2n2-n）-[2（n-1）2-（n-1）]=4n-3。

当n=1时,a1=1也符合上式,所以数列{an}的通项公式为an=4n-3。

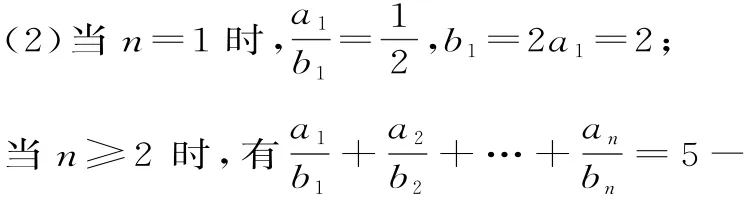
又因为S3=2a3-1,所以a1+2a1+4a1=8a1-1,解得a1=1,an=2n-1。

（2）由 （1）知,bn=log2（an+1·an）=log2（2n×2n-1）=2n-1。

68.（1）当n=1时,a21+2a1=4S1+3=4a1+3,因为an＞0,所以a1=3。

70.（1）设数列{an}的公差为d。

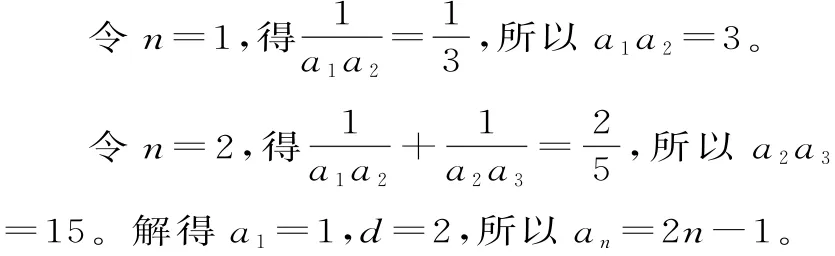
（2）由（1）知bn=2n·22n-1=n·4n。

所以Tn=1·41+2·42+…+n·4n。

4Tn=1·42+2·43+…+（n-1）4n+n·4n+1。

两式相减,得: