基于EWM-TOPSIS模型的房柱式采场布置方案优选研究
2021-06-01李全明褚衍玉史先锋
魏 杰,李全明,褚衍玉,王 虎,史先锋
(1.中国安全生产科学研究院 矿山安全研究所,北京 100012;2.矿山采空区灾害防治国家安全监管总局安全生产重点实验室,北京 100012)
随着石材矿山地下开采的推广,地下开采硐室规模越来越大,随之而来的安全隐患也越来越多。对于地下矿山,采场布置参数是决定矿山安全和高效生产的重要参数[1-2]。合理的采场布置方案,不仅要保证采场开采期间的安全性,还应尽可能提高矿石的回收率,以保障矿山的经济效益。因此采场布置方案的优选是一个涉及多层次、多参数的决策过程,需综合对采场的安全性和经济性两方面效益进行比较来确定最优参数[3]。传统地下矿山采场布置方案的优选多采用经验法和工程类比法来决定,这些方法受决策人的专业知识、经验等主观因素影响较大,难以综合考虑各方面因素的影响,具有极大的主观性及随意性,确定的采场参数也难以兼顾矿山的安全和经济效益[4]。近年来,数学分析方法被越来越多地运用于矿山工程方案优选中,文献[5]建立了基于相似优选比原理和模糊数学原理的多因素决策模型,对采矿方法的技术经济指标进行综合评价,从而实现对采矿方法进行优选;文献[6]采用层次分析法和模糊数学法建立了采矿方案优化综合评判体系,对各个采矿方案参数进行优选,最终由模糊矩阵选出最优方案参数;文献[7]通过神经网络法研究了一种用于优化煤矿地下采场结构参数的算法,并成功运用于实际采矿工程中;文献[8]基于人工鱼群算法、响应面法和Vague理论,构建了优化采场结构参数的Vague-RSM-AFSA模型,实现量化采场结构参数的优越度,以此来对采场结构参数进行优化。
上述分析方法的应用弥补了传统方法在决策分析中受单因素和主观因素影响的缺陷,在一定程度上实现了对评价对象的客观优选,但上述分析方法在指标权重的确定方面均存在一定的不足,而且部分方法无法确定复杂指标体系的权重,因此不适用于复杂指标方案的优选。
优劣解距离法(technique for order preference by similarity to ideal solution,TOPSIS)[9-11]是一种通过求解有限个评价对象与目标最优解的接近程度来确定评价对象优劣性的多目标决策分析方法,被广泛应用于矿井安全领域决策分析和工程设计方案优选当中。优劣解距离法能充分利用原始数据的信息,在计算过程中消除数据不同量纲的影响,因此可以引入不同量纲的评价指标进行综合评价,评价结果能定性反映不同评价对象的优劣程度。另外,鉴于传统分析方法指标权重系数确定不合理的难题,本文在TOPSIS法的基础上引入熵权法(entropy weight method,EWM)[12-13]来确定指标权重,建立EWM-TOPSIS综合指标评价模型,进一步优化评价指标,使其更具客观性,从而保障评价结果更具可靠性和合理性。
1 采场布置方案评价指标体系建立
评价指标体系的确定是采场方案优化的重要前提,这一基本工作的科学性对整个评价结果的合理性有着直接影响。在整个评价指标体系中,各因素间既相互联系,又相互制约,在评价指标的选取上,应本着高效准确的原则,尽量选取少的指标,反应最主要和最全面的信息。
矿山生产中,安全与经济的矛盾始终存在,以地下石材矿山为例进行分析。石材矿山为提高石材生产的成材率和品质,常采用房柱式采矿法进行开采,其地下采场的稳定性决定于矿房和矿柱尺寸等采场布置参数的合理与否[14]。采场布置参数过于保守,能够保障矿山生产的安全,防止事故的发生,但会导致企业经济效益的降低;采场结构参数过于激进,虽能提高矿山开采效率和经济效益,却不能保证采场的安全性。因此,确定合理的采场参数,应统筹兼顾采场安全与经济两方面因素,即在确保安全的前提下,最大限度地提高矿石回收率,以确保矿山的经济效益。根据房柱式采场的工艺特点,确定采场安全性指标包括:顶板的最大拉、压应力,顶板的竖直位移,矿柱的最大拉、压应力,矿柱的竖直位移;经济性指标则主要为采场的矿石回收率。
基于上述分析,建立采场布置方案评价指标体系,如图1所示。
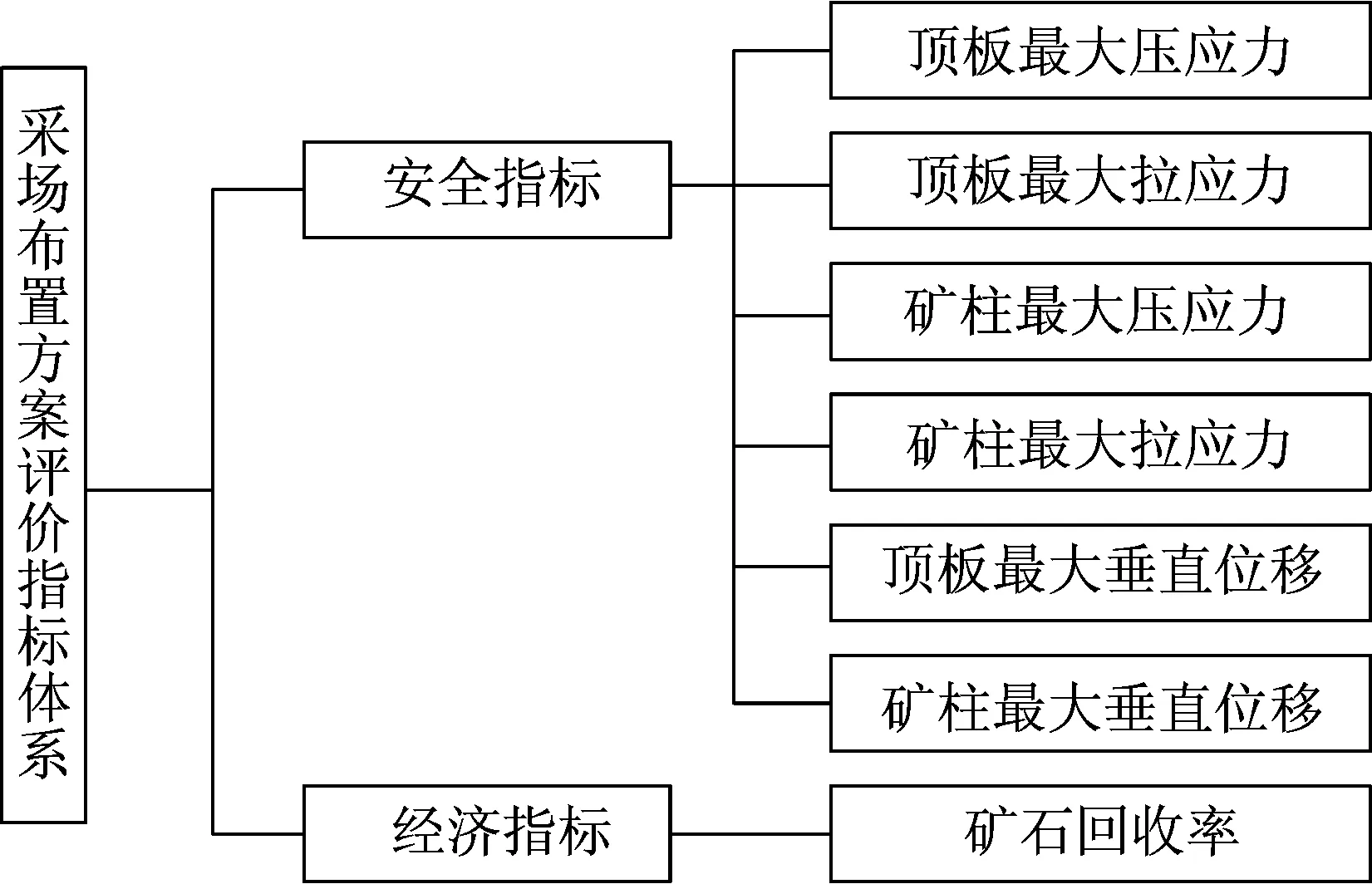
图1 采场布置方案评价指标体系
2 EWM-TOPSIS指标评价模型的建立
(1) 构建决策矩阵Z。根据采场布置方案的指标体系,建立多属性决策矩阵,即
(1)
其中,xij(i=1,2,…,m;j=1,2,…,n)为第i个方案的第j个指标参数值。
(2)决策矩阵标准化处理。因为决策矩阵中各类参数的单位不统一,所以对矩阵进行无量纲标准化处理。常用的标准化方法是平均值法,计算第j个指标下第i个方案的指标值比重dij,则可得:
(2)
(3)基于EWM法确定指标权重。在多指标决策问题中,以指标权重系数来表示各个指标的重要程度。
因此确定合理指标权重是整个采矿方案优选过程中最重要的步骤。
根据信息论的基本原理,信息是系统有序程度的一个度量,而熵是反映系统无序程度的一个度量,信息量越大,系统无序性越小,熵值越小[15],因此信息熵能比较客观地评价指标的有序度与效用。EWM法是一种客观赋权方法,实际运用中,EWM法根据各指标的变异程度,利用信息熵计算出各指标的熵权,再通过熵权对各指标的权重进行修正,从而可以得出较为客观的指标权重。
首先,计算第j个指标的信息熵S(dj)和输出熵C(dj),即
(3)
(4)
然后,计算第j个指标对应的差异系数H(dj),可得:
H(dj)=1-C(dj)
(5)
最后,计算第j个指标的权重Wj,即
(6)
根据(6)式可计算出每个指标的权重,指标权重向量为:
(7)
(4)构建加权决策矩阵V。则有:
V=(vij)m×n=(Wjdij)m×n
(8)
(5)确定正、负理想解C+、C-。则有:
C+={(maxvij|j∈J1),(minvij|j∈J2)},
C-={(minvij|j∈J1),(maxvij|j∈J2)}
(9)
其中:J1为安全性指标集合;J2为经济性指标集合。
(6)根据正负理想解,计算各评价对象到理想解的接近程度,与正理想解越接近的评价对象即为最优评价对象,则有:
(10)
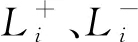
3 实例分析
四川某大理石石材矿山,原为露天开采,近年来由于受环保因素影响逐渐转为地下开采,企业为提高矿石的成材率,采用房柱式采矿法进行开采,以采高20 m、推进深度60 m布置采场,根据理论分析确定了3种采场布置方案,各方案采场布置参数见表1所列。

表1 各方案采场布置参数 m
通过数值模拟方法对3种方案进行分析,得到各方案下采场的安全性和经济性指标参数,见表2所列。
针对3种备选方案,建立采场布置方案综合评判指标体系。并根据方案指标参数(表2)构造决策矩阵Z,再根据(2)式对决策矩阵Z进行无量纲标准化处理,得到标准化矩阵Z′,即

表2 各方案指标参数汇总

(11)

(12)
根据EWM法原理,基于(3)~(6)式确定权重向量W;再由标准化矩阵Z′和W,根据(8)式计算得出加权决策矩阵V;最后根据(9)式计算正、负理想解C+、C-。得到的W、V、C+、C-分别为:
(13)

(14)
C+={0.062 6,0.020 2,0.005 4,0.017 0,0.007 7,0.001 5}
C-={0.100 6,0.025 8,0.006 2,0.267 3,0.021 4,0.008 9,0.001 4}
(15)


表3 各方案综合评价结果

4 结 论
(1) 针对地下石材矿山房柱式采场工艺特点,从安全性和经济性两方面考虑,选取7个主要指标构建了采场布置方案评价指标体系,并利用EWM法计算出了各参评指标的权重,弥补了传统决策分析方法指标权重设置不合理的缺陷。
(2) 在TOPSIS法的基础上,建立了EWM-TOPSIS综合指标评价模型,并应用于某地下石材矿山采场布置方案的优选,经计算分析,得到采场各方案的优劣顺序,最终确定方案Ⅰ为采场的最优布置方案。
(3) EWM-TOPSIS综合指标评价模型结合了EWM法和TOPSIS法的双重优点,既能够充分利用原始数据信息来构建评价指标,也能对参评指标进行合理赋权,保证了评价结果的科学性与合理性,对于解决房柱式采场方案优选的难题具有实际意义,也为相似工程的解决提供了参考。
