阿舍勒铜矿二步骤采场回采充填体稳定性分析

文 兴 赵 亮 黄 敏

(1.长沙矿山研究院有限责任公司，长沙 410012；2.金属矿山安全技术国家重点实验室，长沙 410012)

随着矿山充填采矿技术的发展，阶段空场嗣后充填二步骤回采工艺在地下矿山得到了广泛应用[1-2]。二步骤回采过程中，一步骤开采矿房，采用尾砂胶结充填，二步骤，开采矿柱采用尾砂充填或废石充填，矿房充填体(即一步骤充填体)将作为矿柱回采时的围岩，其强度和稳定性关系到二步骤采场(矿柱)回采的安全和经济效益[3-4]。目前充填体稳定性的理论计算方法有蔡嗣经验公式法、Terzaghi模型法、Thomas计算法、卢平计算法、Mitchell 计算法等[5]。

随着数值模拟技术的快速发展，计算结果能动态反映开挖和充填过程中围岩的位移、应力及塑性区等变量，越来越多的矿山工程采用数值模拟方法进行稳定性分析[6-14]。如张帅帅等应用 FLAC3D探究胶结充填体内开挖巷道对其稳定性的影响[12]。曾凌方等[13]基于数值模拟对3种充填方案进行了对比，选择了回采安全性最好的充填方案。臧传伟等[14]对上向水平分层充填法，采用理论计算和数值模拟相结合的方法，确定的采场结构参数合理可靠，实现了卧虎山铁矿安全高效的开采。寇永渊等[15]利用ANSY和FLAC3D数值模拟软件，对+1 000 m中段水平矿柱回采期间充填体及地表的应力和位移变化趋势进行分析，揭示二矿区井下充填体及地表在整个回采过程中的动态地压分布规律，综合评价了二矿区+1 000 m水平矿柱回采期间充填体的稳定性。

本文以阿舍勒铜矿深部一步骤采场充填体为研究对象，采用理论计算和数值模拟相结合的方法，计算和研究二步骤采场开挖后两侧充填体的稳定性，客观分析和评价一步骤采场充填的合理性，为矿山采场充填设计优化和二步骤采场回采工艺优化提供依据，对矿山深部采场安全开采和技术经济指标控制具有重要意义。

1 工程背景

阿舍勒铜矿深部采用大直径深孔阶段空场嗣后充填采矿法，一步骤开采矿房，隔一采一，采用尾砂胶结充填。采场垂直于矿体走向布置，采场宽12.5 m、长30～40 m、高50 m，实际充填高度为55 m(含凿岩硐室5 m)，主要采用1∶4、1∶6和1∶8的灰砂比充填体，充填设计根据现场情况确定，0 m中段北1#采场为二步骤采场，其两侧分别为北2 #采场和0 #采场，为一步骤回采采场，充填设计如图1、图2所示。

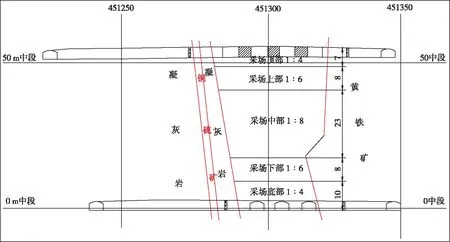
图1 0 m北2#采场充填设计示意图

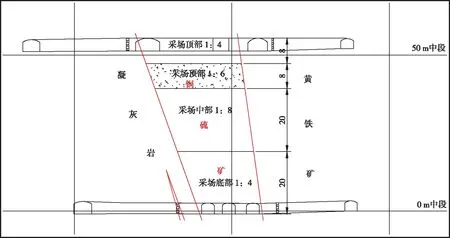
图2 0 m中段0#采场充填设计示意图

2 充填体稳定性理论计算

充填体稳定性理论分析主要通过对充填体受力状态及围岩相互作用进行一定的条件假设，求出充填体内应力与充填体暴露参数之间的关系，并以此为依据，确定充填体保持稳定所需强度[16]。考虑不同计算方法的原理和使用条件，结合阿舍勒铜矿充填采矿现状，本文采用Thomas计算法和Mitchell 计算法对一步骤采场胶结充填体强度分别进行了计算。Thomas计算法计算充填体底板的垂直应力公式见式1。Mitchell 计算法计算充填体矿柱的安全系数计算公式如式2。

(1)

(2)

式1中，h—暴露的充填体高度，m；w—暴露的充填体宽度，m；γ—充填体密度，kN/m3；σv—作用在充填体底部的垂直应力，MPa。计算时，γ取16.5 kN/m3，h取50 m，w取30 m，计算得出充填体底板的垂直应力σv=0.31 MPa。深部一步骤采场底部充填体强度设计值一般>3 MPa，因此，采场底部充填体强度满足要求，一步骤采场底部充填体稳定性较好。

式2中，C—充填体的内聚力，MPa；φ—充填体的内摩擦角，°；B—充填体宽度，m；H—暴露的采场高度，m；L—采场充填体的平面暴露长度，m；γ—充填体密度，kN/m3；ψ—平面破坏角，ψ=45+φ/2，°；Wnet—滑动块体质量，kg；He—滑动块体的有效高度，He=H-(B×tanψ)/2，m。计算时，充填体内聚力C取0.2 MPa，内摩擦角φ取27.5°，充填体宽度B取12.5 m，暴露的采场总高度H取50 m，采场充填体的平面暴露长度L取30 m，γ取16.5 kN/m3。计算得出北1 #采场两侧充填体底部安全系数为2.6，中部(暴露高度25 m)安全系数为1.8，充填体安全、稳定、可靠。

3 充填体稳定性数值模拟计算

为了进一步研究二步骤采场开挖后，其两侧胶结充填体的稳定性，采用数值模拟方法进行计算分析，本文计算采用加拿大Rocscience系列岩土专业软件中的Phase 2。

3.1 数值模拟计算方案

以0 m中段北1 #采场为研究对象，该采场位于1号矿体9 #与7 #勘探线之间，采场宽12.5 m，矿体平均倾角81°，矿体平均厚度约28.5 m，其北侧为北2 #采场，南侧为0 #采场。基于Phase 2软件建立数值模拟模型如图3所示，模型共950个单元，502个节点。数值模拟计算采用Mohr-Coulomb本构模型。模拟采用的材料力学参数见表1。首先进行原岩应力平衡，其次对0 m北2#采场开挖，再对0#采场开挖和充填，最后对0 m北1#采场进行开挖模拟。

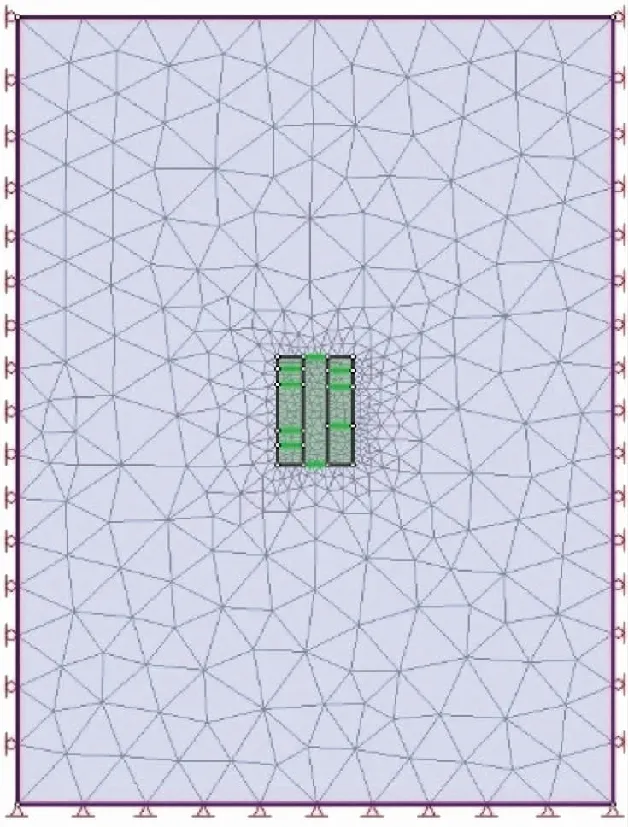
图3 数值计算模型和网格图

表1 矿岩体及充填体材料物理力学参数

3.2 数值模拟计算结果分析

从整体位移量、最大主应力、最小主应力及塑性区四个方面进行对比分析，综合分析0 m中段北1 #采场开挖后，采场两侧充填体的稳定性状况。

1)位移计算结果分析

0 m中段北1 #采场开挖后，整体位移云图如图4所示。从图4可以看出，采场两侧充填体整体位移随着高度的变化均呈现出逐渐递增的趋势，采场底板两边角位置处整体位移较小，最小值为2.07 cm，采场顶板两边角位置处整体位移较大，最大值为4.17 cm，其中0 #采场一侧的整体位移稍大于北2 #采场一侧的整体位移。这是因为，0#采场中部1∶8灰砂比充填体厚度较大，且与下部充填体材料属性相差较大，而北2 #采场上下充填体的灰砂比分配较为均匀。

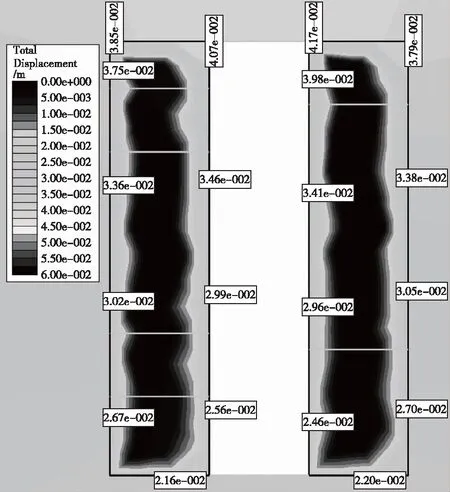
图4 整体位移云图

采场两侧的整体位移随充填体高度变化情况如图5所示。从图5可以看出，采场侧帮整体位移较为接近，两者变化趋势大体相同，在重力及侧帮应力释放的共同作用下，采场侧帮整体位移随着采场高度的增加而逐渐增加，最大位移发生在顶板两端角位置。总体来看，两侧帮充填体整体位移量较小，表明两侧充填体稳定性较好，发生垮塌、冒落的可能性较小。

图5 开挖后采场两侧整体位移变化

2)应力计算结果分析

0 m中段北1 #采场开挖后，采场最大主应力与最小主应力云图如图6、图7所示。采场两侧的应力随采场侧帮高度变化情况如图8、图9所示。从应力计算结果可知，采场两侧帮充填体最大主应力随着充填体侧帮高度的增大呈现出先减小后增大的趋势，由1.19～3.29 MPa逐渐减小为0.59～0.86 MPa，之后又逐渐增大为1.02～1.31 MPa，表明充填体侧帮最大主应力在两侧帮中央位置得到了充分释放。另外，0 m中段0#采场一侧的最大主应力稍小于北2#采场一侧的最大主应力。这是因为，0 #采场下部1∶4灰砂比充填体厚度较大、强度高、支撑能力强。最大主应力普遍小于充填体的极限抗压强度(1∶4、1∶6、1∶8灰砂比充填体抗压强度分别为3.0、2.0、1.5 MPa)，只在采场边角处出现了局部超过充填体极限抗压强度情况。采场两侧帮充填体最小主应力随着充填体侧帮高度的增大呈现出逐渐减小的趋势，由0.36～1.21 MPa逐渐减小为-0.06～0.07 MPa，表明侧帮充填体由压应力状态逐渐转换为拉应力状态，应力在两侧帮位置得到了充分释放，但拉应力集中区域较小，且均未超过对应位置充填体的极限抗拉强度(1∶4、1∶6、1∶8灰砂比充填体抗拉强度分别为0.2、0.1、0.05 MPa)。

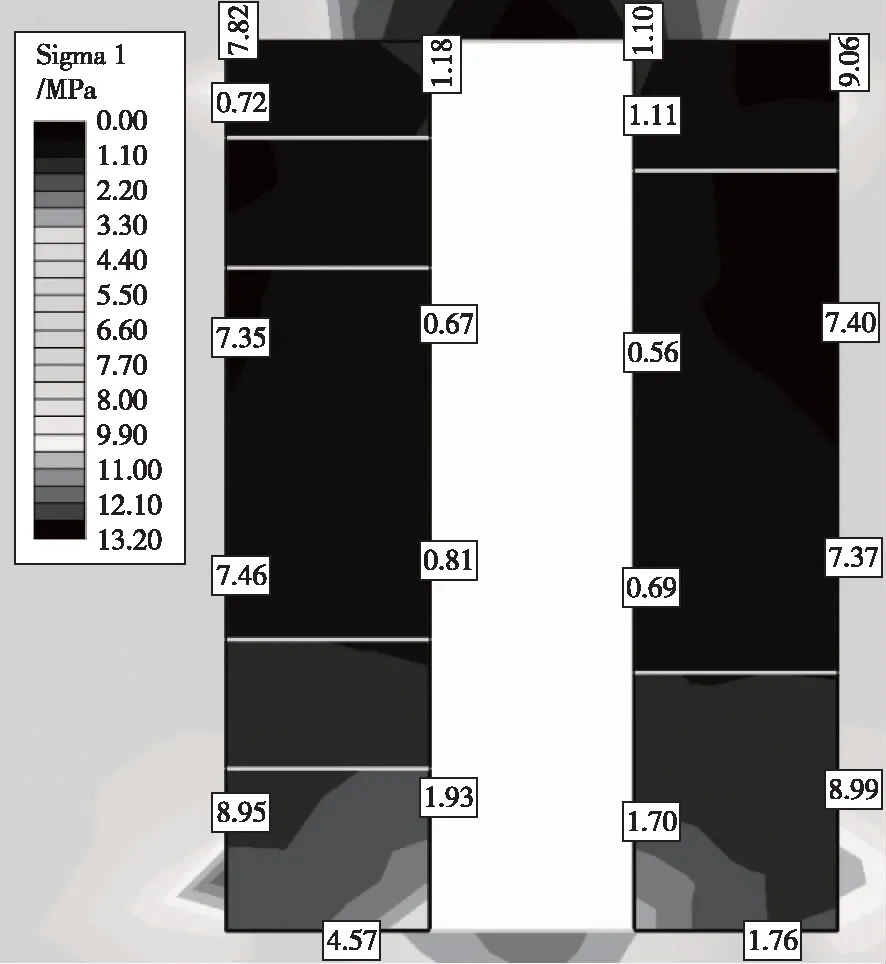
图6 开挖后采场两侧最大主应力分布云图

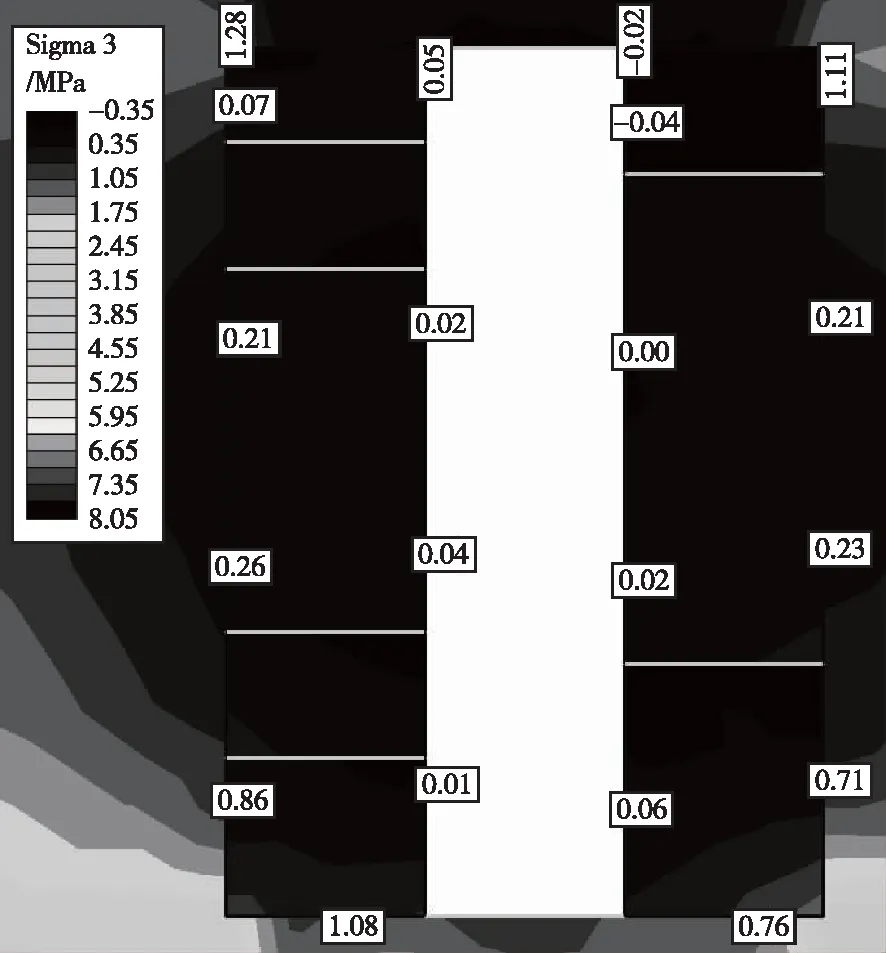
图7 开挖后采场两侧最小主应力分布云图

图8 开挖后采场两侧最大主应力变化

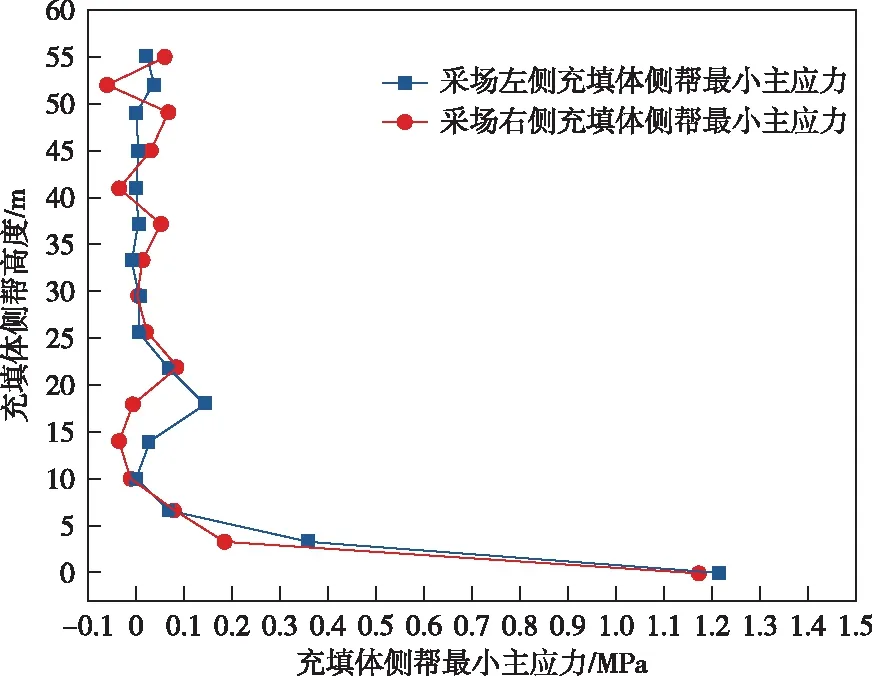
图9 开挖后采场两侧最小主应力变化

综上，0 m中段北1 #采场开挖后，采场两侧的充填体稳定性较好，产生大范围垮塌、冒落的可能性小。

3)塑性区计算结果分析

0 m中段北1 #采场开挖后，采场两侧充填体的塑性区分布如图10所示。从图10可以看出，充填体内部塑性区主要分布在不同灰砂比充填体的交界面以及采场两侧充填体边角部位，破坏趋势均为拉伸破坏。总体来说，塑性区分布范围有限，且塑性区拉伸破坏区域未大范围相互贯通，由此可以得出，北1 #采场开挖后，采场两侧充填体稳定性较好，不会产生大范围的垮塌、冒落。

图10 0 m中段北1#采场开挖后塑性区分布

4 结论

1)一步骤采场设计充填强度大于计算得到的稳定性所需强度，满足采场二步骤开采技术要求。二步骤采场开挖后，两侧充填体整体稳定性较好。

2)二步骤采场回采后，最大位移发生在顶板两端角位置，侧帮位移整体较小；充填体两帮应力得到了充分释放，最大主应力普遍小于采场的极限抗压强度。塑性区分布有限，且拉伸破坏区域未出现大范围相互贯通，采场两侧充填体的稳定性较好，产生大范围垮塌、冒落的可能性小。

3)试验采场两侧一步骤采场充填设计强度能满足开采要求，充填体稳定性良好，有较高的安全系数。