进给系统爬行对沟道磨床精度的影响研究
2021-06-01梁兵兵赵小勇朱嘉敏周庆成
梁兵兵,王 勇,赵小勇,朱嘉敏,金 平,周庆成
(1.合肥工业大学 机械工程学院,安徽 合肥 230009;2.安徽力成机械装备有限公司,安徽 池州 247100)
QMB125球笼沟道磨床常用于球笼钟形壳弧球道粗精磨,加工沟道的直径范围在45~100 mm,沟道的加工过程由星形套的摆动和砂轮在导轨上的移动以及砂轮的磨削共同组成,因此砂轮随工作台在导轨上的进给运动对被加工工件的精度有很大影响[1]。进给系统低速进给时易出现爬行现象,爬行导致切削稳定性下降,使得加工精度降低[2],因此,研究沟道磨床进给系统的爬行机理,对提高被加工工件的加工精度和表面质量有重要意义。
近年来,关于机床进给系统的爬行问题有较多研究文献,但对沟道磨床方面的研究却很少。文献[3]在对数控机床的动力学仿真中,通过改变丝杆的转速,对工作台上同一点在不同转速下的振幅情况,以及不同点在同一转速下的振幅情况进行了分析,但对影响工作台振幅的具体因素没有深入研究;文献[4]通过对电机直连滚珠丝杠工作台式进给系统进行数值仿真,获得了阻尼,刚度,静、动摩擦因数差及Stribeck速度等参数对爬行频率的影响规律,但对各影响因素之间的耦合问题没有深入研究。QMB125球笼沟道磨床是汽车等速传动轴加工的重要装备,本文通过模拟QMB125球笼沟道磨床的进给过程,获得连续的进给数据,并分析影响磨床磨削精度的因素。
1 伺服进给系统爬行分析
1.1 磨床进给系统组成
QMB125球笼沟道磨床长2 200 mm,宽1 800 mm,高2 150 mm,如图1所示。该磨床主要包括床身、立柱、主轴箱、摆动回转台、定位夹具、沟道磨削砂轮、摆动传动组件等。当磨床工作时,砂轮随工作台在导轨上进给到给定位置,摆动回转台会以固定的角度来回旋转,在当前工位加工完毕,定位夹具会旋转至下一工位继续加工。
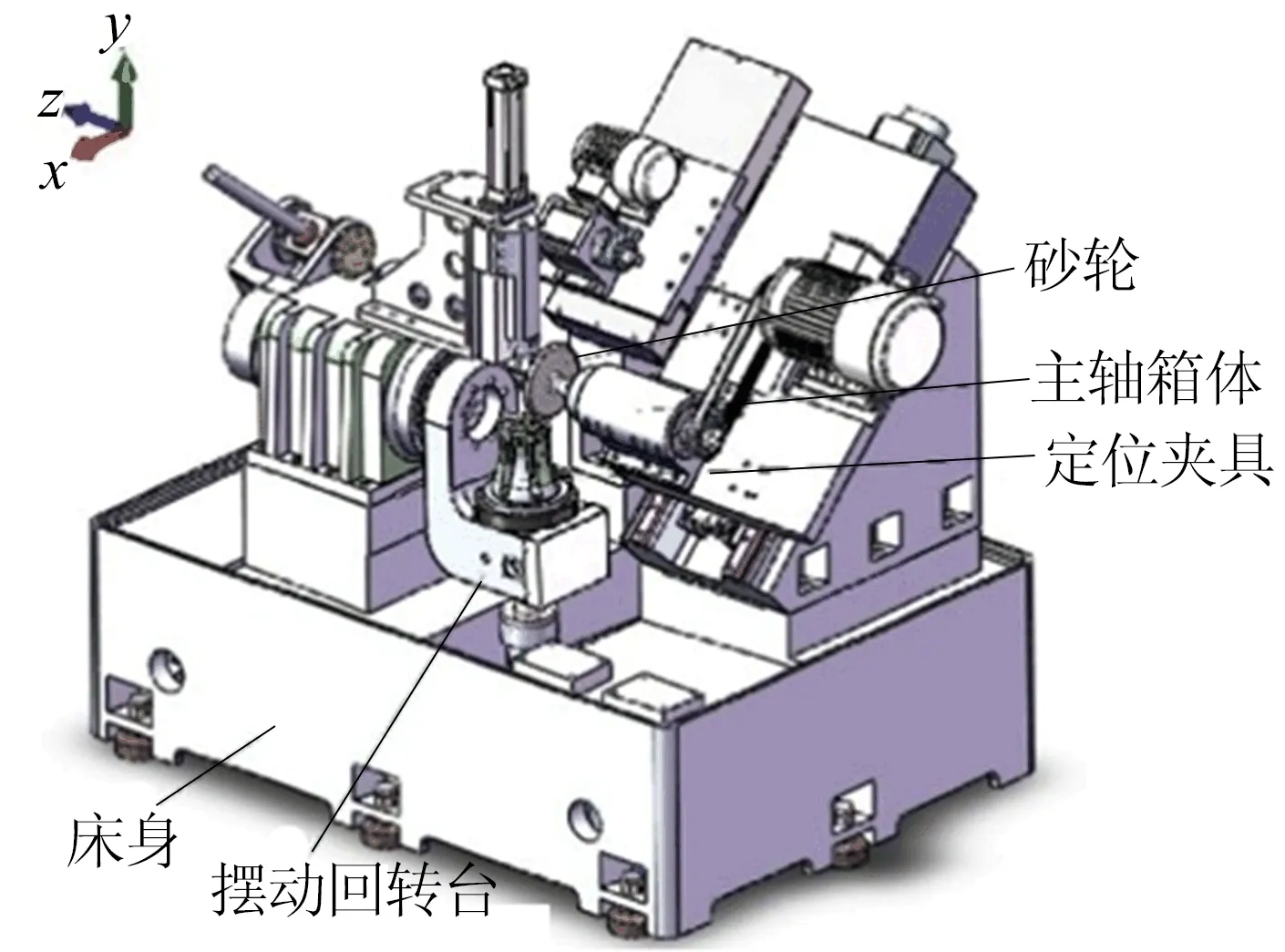
图1 QMB125球笼沟道磨床
磨床的进给系统结构示意图如图2所示,伺服进给系统由交流伺服电机、联轴器、丝杠、丝杠螺母、工作台等组成。
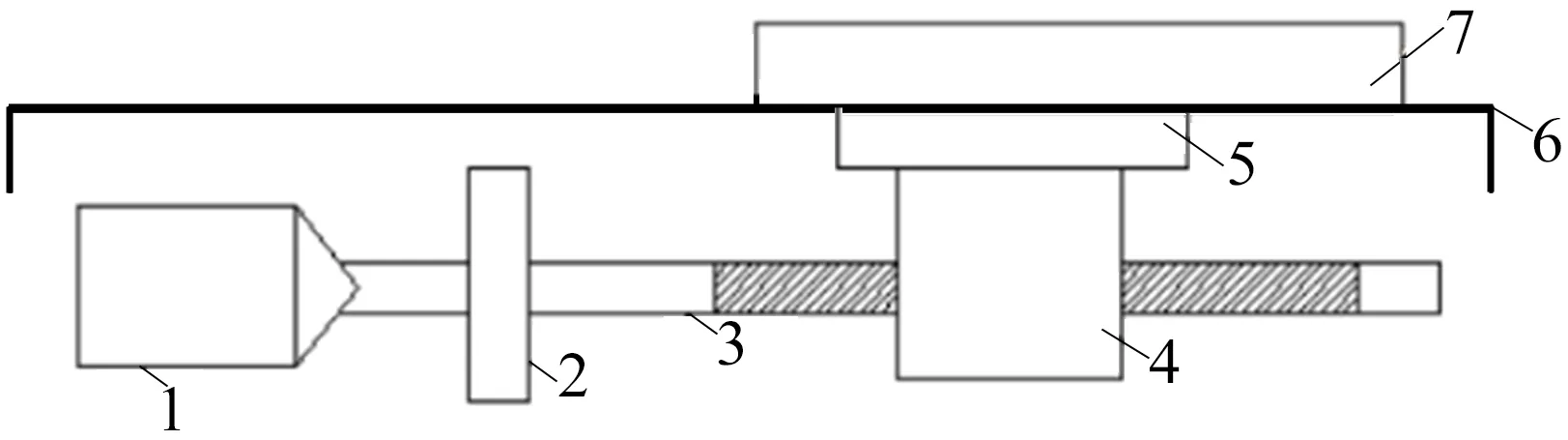
1.电机 2.联轴器 3.丝杠 4.丝杠螺母 5.螺母座 6.导轨 7.工作台
1.2 爬行原理
磨床的伺服进给系统是一个动力学系统,可等效为弹簧质量振动系统[5],如图3所示,等效刚度为k,等效阻尼系数为c,工作台和砂轮为从动件,质量为m,与导轨产生摩擦力Ff,伺服电机的转动作为系统的输入,从动件的移动位移作为输出。进给系统的驱动速度为v0,从动件的平移速度为v1。
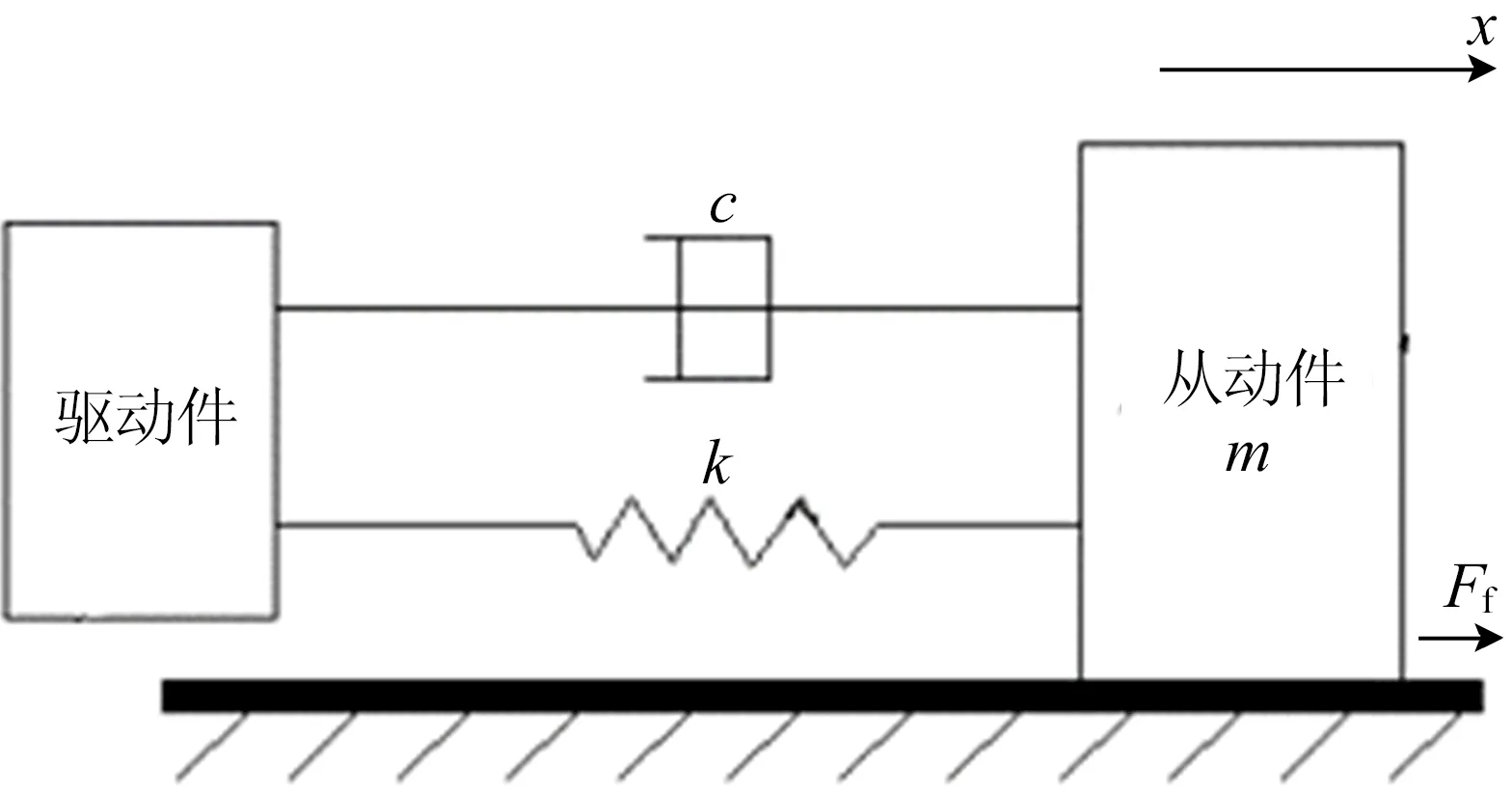
图3 进给系统等效物理模型
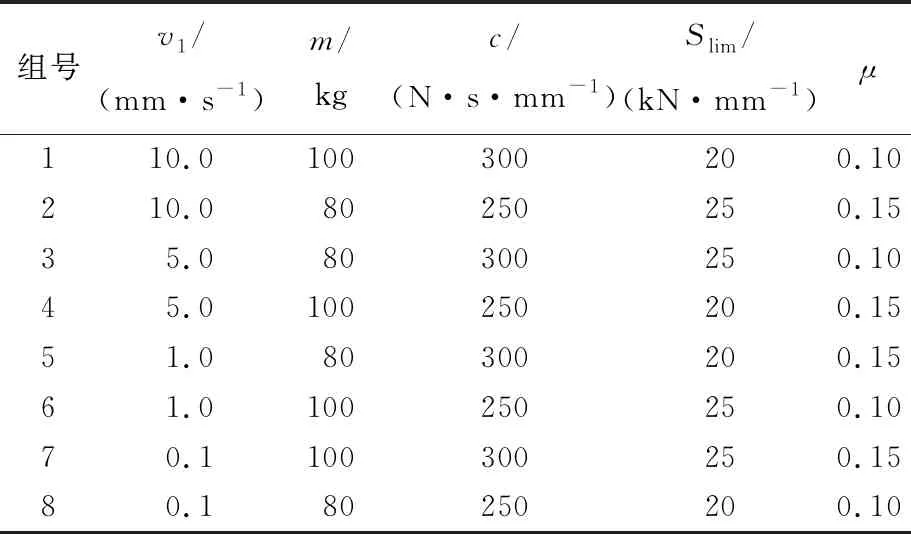
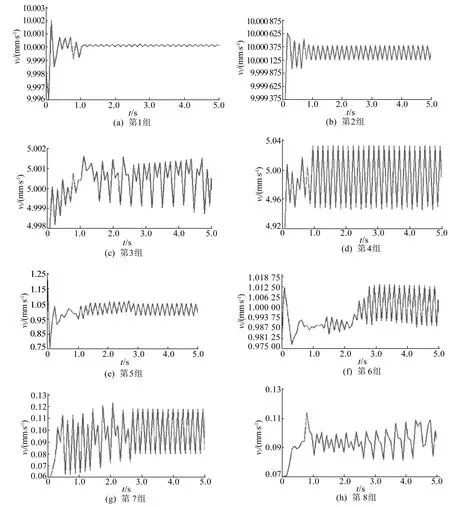
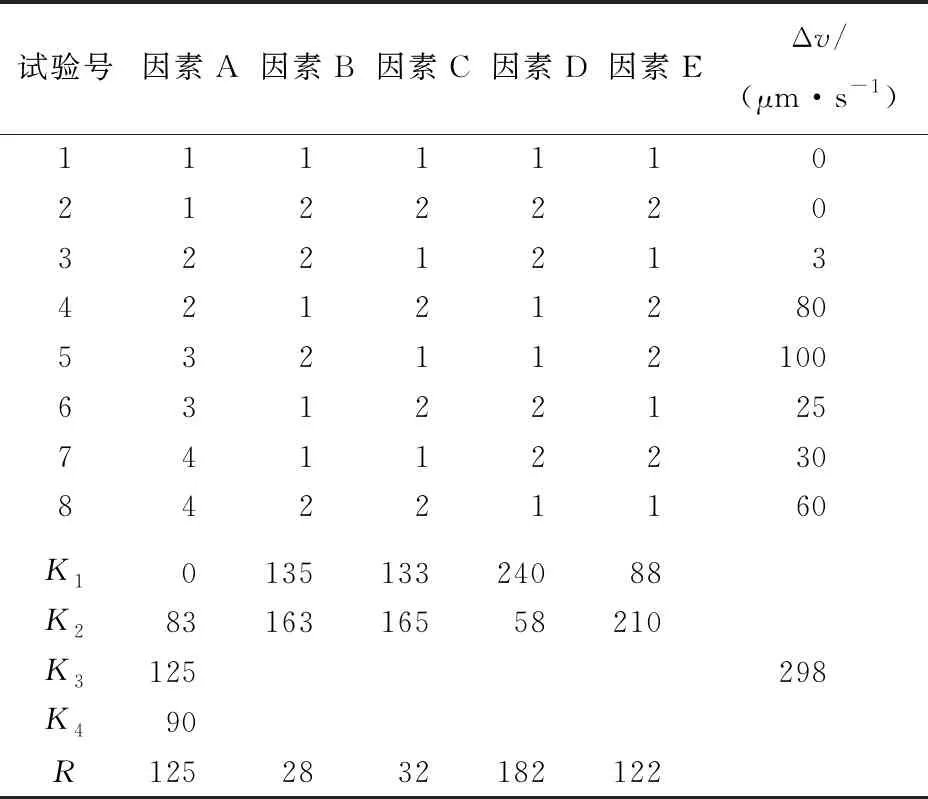
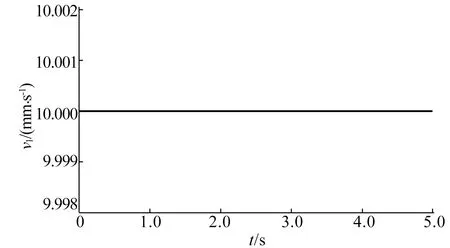
在电机启动后,系统产生弹簧力Fk、静摩擦力Ffs及阻尼力Fc,由于Fc和Ffs的阻碍作用,在驱动后一小段时间,有Fk 设经过时间t,从动件位移为x,利用经典控制理论对上述弹簧质量系统建立数学模型[6]为: mx″+c(x′-v0)+k(x-v0t)=-Ff (1) 其中:x′-v0为工作台瞬时平移速度v1与驱动速度v0之间的差值;x-v0t为等效模型中弹簧的伸长量。 若系统无爬行现象,则进给速度不变,Ff=Ffw恒定不变,可将(1)式简化为: k(xw-v0t)=-Ffw (2) 此时,弹簧力k(xw-v0t)与稳态摩擦力Ffw平衡。 若系统出现爬行现象,工作台的瞬时位移x将偏离稳态值xw,设偏离量为xΔ,则位移x可表示为: x=xw+xΔ (3) 工作台的瞬时速度x′可表示为: x′=xw′+xΔ′=v0+xΔ′ (4) Ff变化量为FΔ,此时有: Ff=Ffw+FΔ (5) 将(2)~(5)式代入(1)式,可得: mxΔ″+cxΔ′+kxΔ=-FΔ (6) 不难看出,影响磨床磨削稳定性的因素有工作台质量m、系统阻尼系数c、等效弹簧刚度k,此外,Ff随着时间的变化产生的变化量FΔ对磨削稳定性也产生影响。为了更清晰描述FΔ对沟道磨床磨削稳定性的影响,不妨设在Δt时间内,Ff与xΔ′存在函数关系,即 Ff=Ffw+f(xΔ′) (7) 当Δt→0时,这种函数关系可近似为线性关系[7],设比例系数为c1,即 Ff=Ffw+c1xΔ′ (8) 将(8)式代入(5)式、(6)式得: mxΔ″+(c+c1)xΔ′+kxΔ=0 (9) (9)式是一个典型二阶系统,阻尼比ξ为: (10) 当0<ξ<1时,二阶系统处于欠阻尼状态。系统输入的能量全部被系统阻尼和摩擦消耗,最后趋于匀速运动,会产生爬行现象;当ξ=1时,系统处于临界阻尼状态,系统输入的能量和输出的能量相等,不会出现爬行现象;当ξ>1时,系统稳定,速度呈指数上升,不会出现爬行现象。 由(9)式解得: xΔ=e-ξ ωnt(Asinωdt+Bcosωdt) (11) 设系统经过时间t0后,作用在从动件上的力正好等于导轨间的最大静摩擦力Ffs,从动件即将运动,在这一瞬间有: Ffs=cv0+kv0t (12) Ffs将在这一瞬间转变为Ffd,此时有: mxΔ″-cv0-kv0t=-Ffd (13) 综合(12)式、(13)式可得: (14) 对(11)式求一阶、二阶导数,并带入初始值得: (15) (16) 将(15)式、(16)式代入(11)式,求得从动件的位移xΔ、速度xΔ′、加速度xΔ″关于时间t的表达式为: (Cξ+1)sinωnt] (17) xΔ′=-v0e-ξ ωnt[(ξ-C)sinωnt+cosωnt] (18) xΔ″=v0ωne-ξ ωnt[Ccosωnt+(1-Cξ)sinωnt] (19) 从(18)式可以看出,当e-ξ ωnt[(ξ-C)sinωnt+cosωnt]<1时,xΔ′很快衰减到0,因此,不出现爬行现象只需: e-ξ ωnt[cosωnt+(ξ-C)sinωnt]=1 (20) 解得: (21) 求得的v0即为爬行临界速度,当进给速度大于临界速度时,不会出现爬行;当进给速度小于临界速度时,出现爬行。 由临界速度的推导公式可以看出,静、动摩擦力之差也是影响爬行的因素,在宏观上表现为静、动摩擦因数之差[8]。 针对QMB125球笼沟道磨床进给系统进行动力学仿真,根据磨床进给机构传动刚度的计算方法[9]可知,沟道磨床出现爬行的条件为: (22) 其中:S为传动系统的当量刚度;Slim为传动系统刚度指标;θ为导轨面与水平面夹角,该沟道磨床夹角θ=45°;μ为静、动摩擦因数之差,系数ψ由导轨和传动系统的阻尼比ξ决定,一般由于爬行时导轨的油膜阻尼较大,ξ、μ、ψ在一定范围内取值[9],ξ取值为0.08~0.12,μ取值为0.01~0.20,ψ取值为0.32~0.58;m的设置不超过200 kg;v1的设置不超过10 mm/s。 综合(10)式、(22)式得出,产生爬行的当量刚度为16~29 kN/mm,阻尼为226~340 N·s/mm。 设定8组不同结构的仿真参数,见表1所列。选取因素A进给速度(v1),因素B质量(m),因素C系统阻尼(c),因素D系统刚度(Slim),因素E静、动摩擦因数之差(μ)5个因素进行正交试验[10]。其中:A1、A2、A3、A4表示v1的4个水平分别为10.0、5.0、1.0、0.1 mm/s;B1、B2表示m的2个水平为100、80 kg;C1、C2表示c的2个水平为300、250 N·s/mm;D1、D2表示Slim的2个水平为20、25 kN/mm;E1、E2表示μ的2个水平为0.10、0.15。 表1 系统仿真参数 将速度波动的范围作为试验指标,选用L8(4×24)正交表,8组试验仿真的速度关于时间变化的曲线如图4所示,采用直观分析法对正交试验的结果进行分析,正交试验表见表2所列。 图4 8组试验仿真曲线 由表2可知,5个因素相互作用对试验指标产生影响,从R值大小顺序可知,对试验指标的影响程度主次顺序为:D→A→E→C→B。根据正交试验可知,该试验要求速度波动值越小越好,因此选取最优水平组合为A1B1C1D2E1。 表2 L8(4×24)正交试验表 基于最优水平组合的参数结构进行仿真,结果如图5所示。从图5可以看出,速度波动为0。 图5 A1B1C1D2E1水平组合下的仿真曲线 由上述对磨床临界爬行速度以及仿真结果的分析可知,提高沟道磨床磨削的精度要从抑制爬行现象入手,应当使工作台进给速度不低于10 mm/s,质量不低于100 kg,系统阻尼不低于300 N·s/mm,系统刚度不低于250 kN/mm,工作台与导轨之间静、动磨擦因数之差不高于0.1。 本文将QMB125沟道磨床伺服进给系统简化为含摩擦的单自由度质量弹簧系统,研究其爬行机理;对伺服进给系统进行了不同结构参数的运动学仿真,并对各影响因素进行正交试验分析,得出了各影响因素之间的耦合关系,并给出抑制爬行的方案,可为沟道磨床进给系统工艺参数优化提供理论依据。2 磨床磨削精度因素分析
2.1 沟道磨床进给系统的数学模型
2.2 临界爬行速度
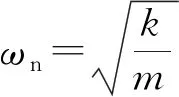
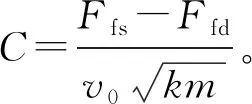
3 影响因素正交试验分析
3.1 仿真参数的确定
3.2 正交试验分析
4 结 论
