冲击倾角下三星型-沙漏型内凹六边形复合微结构面内冲击动力学性能

赵 颖,王凯锋,施劲余,桑 叶,马芳武,李云伍

(1.西南大学 工程技术学院,重庆 400715;2.吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130022)

微结构材料具备轻质和高性能等特点,通过对材料内部微元胞的设计与排布,可以使材料的宏观性能得到改善。其中,负泊松比微结构材料的“压缩-收缩”特性使其具备优异的抗冲击性能和吸能特性。因此,对负泊松比材料力学性能的研究很有意义,同时,开发设计出一种性能更优的微结构材料是非常有必要的。

国内外学者在负泊松比微结构材料方面的研究较多,通过对内凹六边形结构的力学性能进行分析,结果表明随着微元胞胞壁厚度的增大,该结构单位质量吸能量先增加后减少,而碰撞力峰值则相反[1]。同时,有学者对微结构材料加工制造缺陷进行了研究,结果表明,微结构材料的元胞缺失和不同的冲击速度都会对其面内动态性能产生影响,当速度为2 m/s时微元胞数目的缺失量会对微结构的能量吸收产生较大的影响[2]。针对微结构材料刚性下降问题,文献[3]对双材料微结构进行了研究,刚性材料分数的引入会使其双材料负泊松比结构的平台应力得到显著提升,并随着刚性材料分数的增加而增加,同时其对峰值冲击力与比吸能的影响机制有着明显的不同。Li等[4]提出了一种新型蜂窝结构,并通过仿真得出尺寸对其泊松比值影响较大。在面内冲击载荷作用下,推导出了新型星形结构密实应变和动态平台应力的理论表达式[5]。Carta等[6]提出了一种二维多孔结构,通过分析可得折角可提升吸能特性[7]。同样地,也可得到胞元扩张角的大小会对蜂窝材料的平台应力值产生正影响[8]。Hou等[9]对改进后的二维多层次内凹蜂窝结构进行了面内动态性能分析。李振[10]等提出一种并联梯度微结构,结果表明当梯度系数较大时,并联梯度对平台区域有显著提升,吸能能力也随之增大。岑神德[11]提出了一种新型内凹负泊松比结构,并验证其具有更好的抗冲击特性和吸能效果。用双向内凹结构胞元代替传统正方形蜂窝结构,发现该双向内凹结构具有非常优越的吸能特性[12]。

微结构材料研究广泛,但目前大多数研究主要针对单种类型的微元胞展开研究,且大多数研究过程中所施加的载荷为垂向载荷,对不同类型不同结构复合的微结构材料在倾斜荷载下的动态性能分析研究不足。针对上述问题,本文基于三星型-漏斗型内凹六边形(Tristar-funnel re-entrant hexagons,TFRH)复合微结构,如图1所示,采用Hypermesh-Lsdyna联合仿真分析方法研究其在不同冲击角度及不同冲击速度下这一微结构材料的动态响应,并建立其宏观动力学响应与冲击倾角及冲击速度的内在关联,分析总结其碰撞吸能规律,为这一微结构材料在汽车碰撞领域的应用提供数据支持。

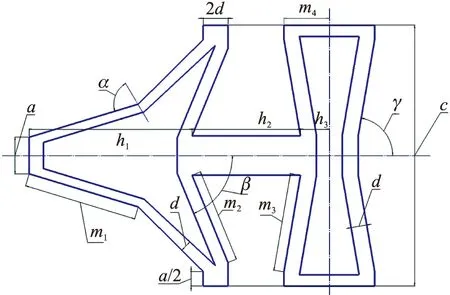
图1 TFRH单胞结构

1 计算模型

1.1 有限元模型

本文应用Hypermesh和Lsdyna联合仿真方法对TFRH复合微结构的面内冲击动力学特性进行分析。如图2所示为不同冲击倾角下TFRH复合微结构材料的面内冲击仿真模型,L1为模型高度,L2为模型宽度。单胞结构之间具有相同的几何结构参数,如表1所示。基体材料采用铝合金,密度ρ=2.75 g/cm3,弹性模量E=69 GPa,泊松比为μ=0.34,屈服应力σzy=0.462 GPa。在有限元模型建立过程中,模型材料采用壳体材料,并使用壳单元,将网格尺寸设置为0.5 mm。此模型沿Y方向的厚度b=2 mm。为保证模型收敛,在厚度方向积分点设置为4。边界条件与文献[5]相同,即倾角为θ的刚性板以冲击速度v对TFRH复合微结构模型沿Z轴正方向进行冲击时,模型底端进行六自由度全约束,并对此微结构的Y轴位移和Y轴旋转两个自由度进行约束。以TFRH复合微元胞为代表性单元,分别沿着X和Z方向填充代表性单元数目为11和6,如图3所示。为保证此模型的计算稳定性,选取时间步长为0.000 01。

图2 冲击加载示意图

表1 模型几何参数

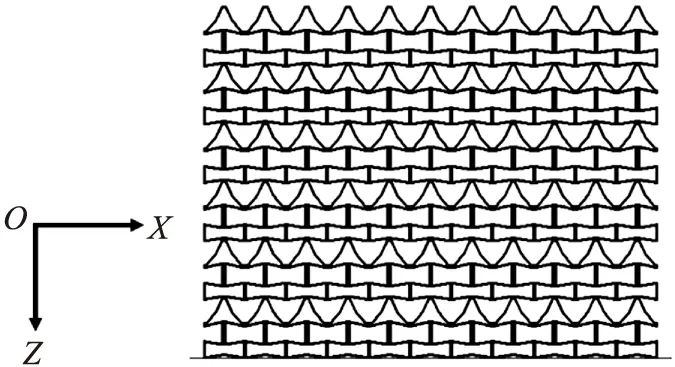
图3 11×6 TFRH复合微结构模型示意图

1.2 模型可靠性验证

为了验证有限元仿真分析模型的可靠性,本文采用电子万能试验机对11×5 TFRH复合微结构试验样件进行面内准静态压缩试验,试验样件为11×5的二维TFRH复合多胞结构,通过3D打印技术制造,基体材料为ABS,材料的密度是1.08 g/cm3。为模拟准静态压缩过程,试验过程中采用位移加载的方式,压头的下行速度设置为10 mm/min。图4为面内准静态压缩试验的设备及3D打印样件。最终获取应力-应变曲线,如图5所示。

图4 TFRH复合微结构准静态压缩试验

从图5看出,分别对比TFRH复合微结构材料的有限元仿真结果和试验结果,可得到两者应力-应变曲线趋势一致,结果相差不大。由于TFRH复合微结构样件在3D打印加工的过程中存在一些微裂纹、弯曲等缺陷,引起样件性能下降。并且由于试验条件存在摩擦,边界条件不理想,试验过程中发生局部胞壁坍塌等原因,试验结果与仿真分析的应力有些许差距,但试验结果与有限元仿真计算结果的整体误差较小,说明了本文所建立TFRH复合微结构仿真分析模型的准确性,并验证了仿真模型的精度。

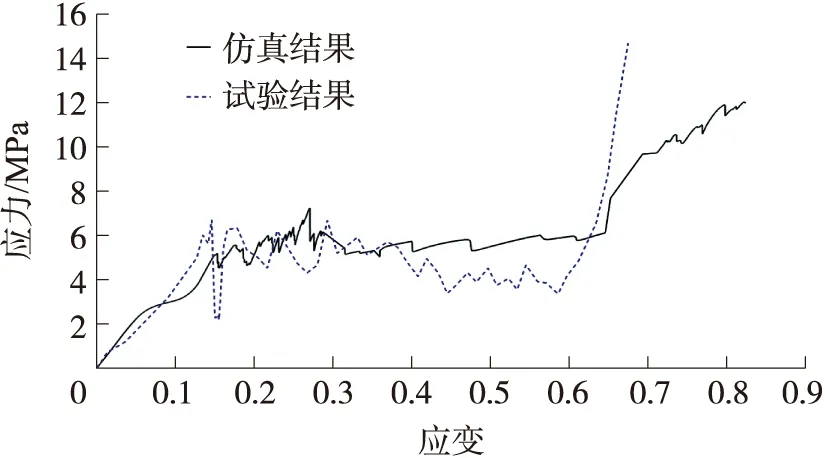
图5 TFRH复合微结构准静态压缩试验结果

2 计算结果与讨论

2.1 微结构材料面内冲击响应

依据前文给出的TFRH复合微结构材料的有限元仿真模型,本文考虑到选取车辆发生碰撞时常用的速度工况,对冲击速度8 m/s、20 m/s和40 m/s分别进行分析,将冲击倾角的范围设置为0～10°。通过对其变形模式和平台应力进行分析,得出TFRH复合微结构在不同冲击倾角和不同冲击速度下的变形过程,如图6所示。

图6 TFRH复合微结构在不同冲击倾角下的面内冲击变形过程

由图6可看出,在冲击过程中,沙漏型微元胞首先产生压缩变形,随着应变的增加,三星型微元胞继而产生压缩变形,此时此微结构材料整体产生“压缩-收缩”的内凹趋势。随着进一步压缩,沙漏型微元胞首先发生弹性变形,而后坍塌的胞壁互相产生接触,产生新的支撑。在此之后,三星型微元胞发生坍塌。随着冲击倾角的逐渐增大,“压缩-收缩”现象越发不明显,材料整体的弯曲倾斜会不断提高,并且更早地出现整体压缩变形。最后,整体压缩变形的趋势会逐渐增大。当冲击速度为8 m/s时,微结构材料从冲击端和底端开始变形,逐渐向中间传播。当冲击速度为20 m/s时,底端的元胞层开始产生变形,随着压缩过程继续进行,冲击端和底端同时产生变形,继而变形朝TFRH复合微结构的中间位置延伸,元胞逐渐失效,微元胞之间的胞壁逐渐相互贴合。当冲击速度为40 m/s时,此材料从冲击端开始被一层一层逐层压溃。不同冲击速度下,TFRH复合微结构材料的动态响应不同,这是由于冲击波在微结构中传播引起的[13]。

由图6还可看出,当冲击速度较低(v=8 m/s):θ=0°时,微结构材料偶数层的漏斗型微元胞首先开始被压缩产生变形,随着压缩应变的增加,三星型微元胞继而产生变形,逐渐形成“S”型的局部变形带;θ=2°时,呈现出一种左倾“井”字型稳定有序的变形模式;随着荷载倾斜角度的增大,θ=4°时,底端的微元胞率先产生变形被压溃,随着压缩的进行,逐渐形成左倾“井”字型稳定有序的变形模式;当θ=6°、θ=8°、θ=10°时,TFRH复合微结构整体均表现出右倾“井”字型稳定有序的变形模式。随着冲击速度的增加(v=20 m/s):θ=0°时,变形模式呈现整体变形模式,没有明显的局部变形带产生;θ=2°时,并没有呈现出稳定有序的变形模式,而是逐渐呈现“S”型局部变形带;θ=4°时的“S”型局部变形模式更加明显;θ=6°时,“S”型变形模式较弱,逐渐呈现右倾“井”字型稳定有序的变形模式;θ=8°、θ=10°时,TFRH复合微结构整体均表现出右倾“井”字型稳定有序的变形模式。当冲击速度进一步增加(v=40 m/s):θ=0°时,变形模式呈现明显的“压缩-收缩”负泊松比变形趋势,呈现“><”的变形模式;随着冲击角度的增加(θ=2°),负泊松比效应逐渐减弱,顶层和底层的微元胞率先产生变形,逐渐呈现“S”型变形模式;θ=4°时,试件冲击端的材料屈服时间进一步缩短;θ=6°时,“S”型变形模式逐渐明显;当冲击角度继续增加(θ=8°、θ=10°)时,呈现出稳定有序的变形模式。

结合以上不同倾斜荷载下的变形模式,将TFRH复合微结构的变形模式汇总如下:当20 m/s≤v≤40 m/s,2°≤θ≤6°时,表现为“S”型变形模式;当20 m/s≤v≤40 m/s,8°≤θ≤10°时,表现为右倾“井”字型稳定有序的变形模式;当v=8 m/s,2°≤θ≤4°时,表现为左倾“井”字型稳定有序的变形模式;当v=8 m/s,θ=0°时,表现为“S”型变形模式;当v=20 m/s,θ=0°时,表现为一般整体变形模式;当v=40 m/s,θ=0°时,表现为“><”压缩-收缩的负泊松比变形模式。

同样地,也可得到相同冲击速度、不同冲击角度下TFRH复合微结构的应力-应变曲线,如图7所示。

图7 同一冲击速度不同冲击角度下TFRH复合微结构应力-应变图

由图7可得,与其他微结构材料类似,TFRH复合微结构仍具有弹性区、平台应力区、平台应力增强区和密实化区。当θ=0°时,材料存在初始应力峰值,随着冲击倾角的增加,初始应力峰值逐渐不明显,第一个平台区也会缩短到忽略不计,两个弹性区与第一个平台应力区可整体看作一个弹性区。同时,发现TFRH复合微结构拥有两组弹性区与平台区,在同一冲击速度下,随着冲击倾角的增加,两个弹性区与中间的平台区将融合在一起,第一个平台区会逐步减小,且随着冲击倾角的增加,弹性区的应力峰值也会逐步降低。同理,在同一冲击速度下,随着冲击倾角的增加,平台区的应力会略微降低,进入平台应力增强区后,在相同应变下(v=20 m/s、θ=2°除外),随着冲击倾角的增大,应力逐渐减小,此规律在TFRH复合微结构进入密实区依旧满足。

同样,当冲击角度相同、冲击速度不同时,还可得到TFRH复合微结构的应力-应变曲线,如图8所示。从图中看出,相同冲击倾角下,TFRH复合微结构的应力随着冲击速度的增加而提升,应力随应变的变化趋势大致相同。

图8 相同冲击角度、不同冲击速度下TFRH复合微结构材料应力-应变图

2.2 平台应力分析

复合微结构材料的平台应力表示为

(1)

式中:εcr代表屈服应变,即名义压缩应力达到第一个应力峰值时的名义应变;ε≤0.9为密实应变,即材料平台应力增强区与密实化区在应变的交点;σ(ε)为名义应力。结合上文曲线分析所得到的εcr和εd,采用MATLAB对应力-应变曲线进行拟合得出σ(ε)表达式,代入式(1)中可得TFRH复合微结构在不同冲击倾角和不同冲击速度下的平台应力值,如表2所示。

表2 不同冲击倾角下TFRH复合微结构平台应力值 MPa

从表2可直观地看出在同一冲击倾角下,TFRH复合微结构的平台应力随冲击速度的增大而增大,这是由于随着冲击速度的增加,材料的惯性效应有所增强,吸能能力提升。而在同一冲击速度下,平台应力值随冲击倾角的增加而下降,这主要由于随着冲击倾角的增加,材料的不对称变形特点变的更显著,较少的微元胞胞壁接触,难以形成更多新的支撑,从而使其平台应力下降。在特定工况下(20 m/s,2°),TFRH复合微结构的变形出现在倾角的垂直方向上,因而相对于v=20 m/s、θ=2°工况下,TFRH复合微结构的平台应力有些许提升。

2.3 能量吸收分析

同理,也可得到相同冲击倾角、不同冲击速度下TFRH复合微结构的能量吸收曲线,如图9所示。由图9可知,在同一冲击倾角下,冲击速度越大,TFRH复合微结构的吸能能力越强,并且在ε≤0.9的范围内,冲击速度v=40 m/s下的TFRH复合微结构吸能量最多。这与上文中得出的同一冲击倾角下,冲击速度越大、平台应力越大的结论一致。

图9 同一冲击角度不同冲击速度下TFRH复合微结构能量吸收曲线图

在相同冲击速度、不同冲击倾角下,还可得到TFRH复合微结构的能量吸收曲线,如图10所示。由图10可知,在同一冲击速度下,随着冲击倾角的增大,TFRH复合微结构的吸能特性不断降低,且当ε≤0.9,θ=0°时,其吸能量最大,满足上文中得出的在同一冲击速度下,冲击倾角越大、平台应力越低的结论。这主要是由于随着冲击倾角的增加,TFRH复合微结构变形时的不对称性增大,较少的胞壁接触不会产生更多的胞壁支撑,从而使其吸能量下降。

图10 同一冲击速度不同冲击角度下TFRH复合微结构能量吸收曲线图

3 结论

本文设计了一种新型TFRH复合微结构,研究了其在不同冲击倾角(0°、2°、4°、6°、8°、10°)、不同冲击速度(8 m/s、20 m/s、40 m/s)下的面内动态冲击特性,研究结果如下:

(1)TFRH复合微结构拥有两组弹性区与平台区,但随着冲击倾角的增加,两个弹性区与中间的平台区会逐渐融合在一起,第一个平台区会逐步减小,其应力-应变曲线也与传统微结构材料的应力-应变曲线相似,弹性区的应力峰值也逐步降低。

(2)在同一冲击速度下,TFRH复合微结构的变形存在不对称性,且随着冲击倾角的增加,其两侧变形差异化加剧,冲击端的冲击点一侧会加快压缩变形,而冲击端的远离冲击点一侧的压缩变形会放缓,在低速时甚至无太大变形,但冲击速度的增加会加快冲击端的变形,降低冲击倾角带来的不对称影响。

(3)通过对平台应力和单位体积吸能的综合分析,发现冲击倾角和冲击速度对TFRH复合微结构的动态响应具有显著的影响,冲击速度越大,其平台应力与单位体积吸能越大。当冲击速度v=40 m/s时,其吸能量和平台应力值最大;冲击倾角越大,平台应力与单位体积吸能越小;当冲击倾角θ=0°时,其吸能量和平台应力值最大。这一影响是由于不对称性变形导致部分材料无法被有效压缩所引起的,为其在汽车碰撞件中的应用提供了良好的数据支持。