基于谱聚类算法的信息资产行为异常检测方法

孟庆杰,尧海昌

(1.南京工业职业技术大学 计算机与软件学院,江苏 南京 210023;2. 南京工业职业技术大学 江苏省教育厅工业软件工程技术研究开发中心,江苏 南京 210023;3.南京邮电大学 计算机学院,江苏 南京 210023)

随着信息技术的普遍应用和持续升级,各类信息安全问题也愈加严重,主要体现在以下几个方面:(1)黑客的攻击手段越来越先进而且越来越隐蔽,新的攻击手段被频繁应用到各类攻击场景中,一般的安全产品如下一代防火墙、下一代入侵检测系统等都无法全面地识别和检测这些攻击[1];(2)计算机用户由于缺乏相关安全意识和安全知识,任意下载和使用各种来路不明的软件或程序,会导致木马、蠕虫、病毒等恶意软件的泛滥,而使用普通的杀毒软件无法彻底清除;(3)在实际IT环境中存在一些别有用心或粗心大意的用户,导致一些重要敏感数据被泄露或滥用,对各类组织的数据安全造成极大隐患。以上问题只是信息安全相关问题的“冰山一角”,在实际运作中存在更为复杂的情况[2]。

有鉴于上述相关信息安全问题,如何快速而精准地发现和定位问题是信息安全研究领域的重要研究方向。近年来,众多学者提出了多种定位和检测信息资产行为异常的方法[3]。其中,王战红[4]提出了一种特征和分类器组合优化的网络入侵检测模型。该模型根据特征、分类器参数对入侵检测结果的影响,设计了两者组合优化的数学模型,改善了入侵检测率。李熠等[5]提出一种稀疏自编码——极限学习机入侵检测模型。该模型通过稀疏自编码器结合编码层的系数惩罚和重构误差对高维数据进行特征提取,再运用极限学习机对提取的特征进行快速有效地精准分类,提升了入侵检测系统性能。He等[6]提出了一种基于深度学习的HTTP隧道木马检测方法。该方法通过从传输层提取隧道木马通信序列特征,结合深度学习中双向反复神经网络构建一种HTTP隧道木马检测模型,提升了网络木马检测效率。Cheng等[7]提出了一种半监督分层叠加时间卷积网络检测模型。该模型是物联网通信中第一个用于异常检测的半监督模型,它可以在标记数据很少的情况下训练未标记数据。此外,该网络还充分考虑了物联网通信中流数据的特点,能够剔除不确定记录,提高了异常检测效率。Alkahtani等[8]提出一种基于深度学习和机器学习的自适应异常检测模型。采用基于长短时记忆递归神经网络的深度学习算法和支持向量机、K近邻的机器学习算法对拒绝服务攻击和分布式拒绝服务攻击进行分类,采用信息增益法从网络数据集中提取相关特征。

由于当前漏洞利用手段先进、种类繁多,当前的异常行为检测方法一种是针对特定应用场景下进行的定制化的检测,另一种是利用已知的特定验证数据集进行研究。随着网络应用场景越来越丰富,网络流量日益增大,信息安全领域出现越来越多的“未知威胁”,即在历史上可能没有出现过的、与当前已有数据集特征完全不同的威胁或风险。

针对没有太多固定特征的威胁数据检测,利用大数据技术以及机器学习技术来解决此类问题是首要之选[9]。本文提出基于谱聚类算法的信息资产行为异常检测方法,该方法主要包含如下步骤:首先,对各类信息资产的相关行为进行特征工程,提取信息资产相关特征。其次,根据特征工程的结果,对相关信息资产建立各类行为基线。基线的建立一般是无监督的,但其建立的正确与否需要用户进行一定的干涉,方可得到可信基线,而且此基线随着时间的推进能够自我演进。需要说明的是,基线是与特定信息资产相关的,即不同的信息资产应具有不同的基线,此基线也可以被称作“资产画像”。再次,将运行数据和基线进行持续比对,如存在一定程度的规则违反则对用户进行提示并提供相关取证数据,包括如统计数据、运行日志、网络协议数据包等。

根据上述分析,对于信息资产的未知威胁检测,其核心问题就是特征工程以及基线的建立。在现实环境中,可以通过旁路嗅探方式方便地获取信息资产的各类网络通信数据,不需要安装代理,但这些网络数据的应用负载多数被加密而无法获得全部明文内容。在现代信息安全的上下文中,很多通信是建立在数据加密基础上的,故在形成行为基线时应考虑到此种因素。

因为特征工程的结果是产出高维向量,故使用传统的统计方法无法获得更为满意的分类结果,而谱聚类算法能够很好地解决该问题。

1 谱聚类算法

谱聚类(Spectral clustering)是一类基于图论的聚类算法,是通过对样本数据的拉普拉斯矩阵(Laplacian matrix)的特征向量进行聚类,从而达到对样本数据进行分类的目的[10]。谱聚类可以理解为将高维空间的数据映射到低维,然后在低维空间,使用其它传统聚类算法(例如K-means算法)再进行聚类。

谱聚类算法效果的焦点在于对样本数据的划分评价,主要的3种谱聚类评价算法差别不是特别明显[11]。考虑到对于信息资产的行为异常检测场景,主要的目标还是针对双路情况(2-way),而多路聚类算法并不是关键的目标,因为该场景下仅需要区分“正常”和“异常”两种情况[12]。

以下给出一般意义下的谱聚类算法。

1.1 相似度矩阵

所谓相似度矩阵主要是指样本点集合V中的任意两个样本点之间的距离度量(Metrics),在聚类算法中表示为距离相近的点之间的相似度较高,而距离较远的点的相似度较低,甚至可以忽略不计[13]。

评价两个样本点相似度算法非常多,比较常见的如余弦相似、Jaccard相似等,而在一般的实现算法中,可以使用余弦相似算法,即假定样本的维度为d,两个样本的余弦相似度为

(1)

式中:xi和xj分别表示集合中的两个样本点,分子部分为向量的点积,分母部分为向量分别取模的乘积,变量sij为这两个样本的相似度。显然此相似度的值介于0与1之间,结果越大则相似度越大。

不同点之间的相似度构成相似度矩阵,而在基于谱聚类算法的相似度评估中,一般可以考虑使用如下3种方式来表示相似度矩阵[14]:

(1)ε-近邻法(ε-neighborhood graph);

(2)K近邻法(K-nearest neighbor graph);

(3)全连接法(Fully connected graph)。

对于方法(1),基本可以忽略不用。因为它主要使用欧氏距离来表示,而且如果距离大于阈值ε,则直接赋为0,否则就固定为ε。而方法(2)和方法(3)比较常用,它们的计算公式分别如式(2)和式(3)所示

wij=wji=

(2)

(3)

式中:wij表示样本xi和样本xj的相似度,‖xi-xj‖为样本间的范数。当然也可以使用一般意义上的欧氏距离、曼哈顿距离或闵可夫斯基等计算。而函数knn(x)表示样本的k近邻,参数σ表示邻域的宽度,默认为1。在一些通用的机器学习工具中如sklearn,一般会使用式(3)来计算两个样本之间的相似度,即使用全连接方式,本文也使用这种方式。另外,使用W来表示由wij构成的相似度矩阵,根据式(3),它实际上是一个n×n的实对称阵,这里n是样本数量。

显然,‖xi-xj‖愈大则表明样本点的相似度越低。当两个样本点重合时,可得wij=1,这与余弦相似度计算所得到的结果基本一致。

1.2 图分割评价

本质上,谱聚类算法是将由n个样本点组成的带权图G=(V,E)进行分割,这里V是图的顶点集合,E是边的集合,边的权值就是顶点间的相似度。对其划分结果的评价依据,主要是各子图内部相似度系数最大化,而子图之间的相似度系数最小化。

在实际谱聚类算法的演进中,出现了很多评价方法[14],如最小割集准则[15]、规范割集准则[16]、比例割集准则[17]、最小最大割集准则[18]、多路(Multi-way)规范割集准则[19]等。根据实际情况,本文主要使用比例割集准则,即RatioCut,以下是相关比例割集准则的说明。

与最小割集准则不同,在比例割集准则中,不仅需要考虑各子图之间的连接权重最小、各子图内部的连接权重最大,还需要考虑各子图中的顶点尽量多。

使用Ai来表示不同的子图,|Ai|表示子图的顶点数量。对于k个子图而言,其优化目标函数如式(4)所示

(4)

(5)

式中:乘以1/2的原因是因为此为双向图,而wij即为相似度,见式(2)。

1.3 拉普拉斯矩阵和目标

对于谱聚类算法而言,其主要工具为拉普拉斯矩阵(Laplacian matrix),一个未标准化的拉普拉斯矩阵如式(6)所示

L=D-W

(6)

式中:矩阵D为计算度矩阵,它是一个对角阵,其对角元素定义为

(7)

从其形式上看,此矩阵的元素是某一个样本点和其他样本点相似度之和,矩阵W是相似度矩阵。

所谓未标准化的拉普拉斯矩阵即它未被单位化,如果需进行单位化可以使用一定方法,主要是两种:一是随机游走标准化;二是对称标准化,分别如式(8)和式(9)所示

L′=D-1L=I-D-1W

(8)

L″=D-1/2LD1/2=I-D-1/2WD1/2

(9)

通过式(8)和式(9)可以看出,拉普拉斯矩阵的标准化实质上是将原始的相似度权值矩阵和度矩阵进行运算,而度矩阵中的元素为相似度之和,故乘以其逆矩阵就相当于做了除法,可以约束其向量范数。需要说明的是,这两种标准化方法并无本质的不同。

在获得拉普拉斯矩阵后,其焦点问题就是如何最小化式(4)中的目标函数。为达到这个目的,首先需定义一类指示向量,以指出当存在n个样本点被划分为k类的情况,这些指示向量之间是相互正交的。定义如式(10)所示(假定有k个指示向量)

(10)

式(10)表明指示向量是各个样本点在不同类中的表示,可以证明式(4)可以最终转化为式(11)表达式

(11)

式中:tr为求矩阵的迹,即矩阵的对角和,此时目标函数化为

Mintr(HLHT),HHT=I

(12)

1.4 算法流程

通过上文分析,谱聚类算法实质是对一类目标函数的极小值求解,对一般谱聚类算法的描述如算法1所示。从时间复杂度而言,求解谱聚类算法是NP的,即无法在多项式时间内进行求解。

算法1谱聚类算法的一般描述

输入:一个含有n个样本点集合;需要分类的参数k

Step1 计算相似度矩阵W,此矩阵规模为n×n;

Step2 计算度矩阵D以及标准化的拉普拉斯矩阵L′,这里使用基于随机游走的标准化矩阵;

Step3 计算随机游走拉普拉斯矩阵的特征值,将这些特征值从小到大进行排序,取前k个特征值对应的特征向量v1,v2,…,vk;

Step4 将上述k个特征向量组合成矩阵V(此矩阵为n×k的);

Step5 对矩阵V进行单位化;

Step6 使用一般的聚类算法,如K-means等对矩阵中的向量进行聚类,即将n个样本聚类成k个类。

输出:已分类的集合A1,A2,…,Ak

1.5 研究内容

考虑在信息安全场景下,主要目标是利用谱聚类算法对信息资产的历史数据进行分析、分类,从而提供对于异常数据的检测依据。故与一般通用的谱聚类算法不同的是,对于k的取值一般很低,比如可能只取两个分类,此时k值为2。

在现实场景下,使用机器学习方法对信息资产的行为进行检测,其最为重要的一环是对数据特征的抽取。有鉴于此,需要有相关特征评价的指标以指导对特征的抽取[20]。本文提出平均差异度指标和簇比例指标结合特征的区分度、关联度进行评估。提出上述指标的目的主要是为了降低或者避免在一般无监督场景下的安全问题误报。下节将对这些指标进行明确定义和说明。

2 特征评价指标

在上节中主要分析了一般意义上的谱聚类算法以及如何求解目标函数等,其算法实质上类似于数据降维。在此基础上本节给出相关评价指标的详细定义并解释其含义。与文献[20]存在一些差异的是,本文的特征相关取值一定是经过归一化的。

特征区分度:所谓特征区分度就是指某特征与其他特征在样本分类中是否更为敏感,其实质上就是其方差是否更为显著,如式(13)所示

(13)

式中:disi表示第i个特征的区分度,aji表示经过归一化后第j个样本的第i个特征的取值。

特征关联度:所谓特征关联度主要是指不同特征的关联情况,与文献[14]不同,本文使用平均协方差来评估,具体如式(14)所示

(14)

式中:d表示特征的维度。显然,此关联度越小,则特征i与其他特征的关联度越低。

利用上述区分度和关联度,定义以下特征重要度指标

impi=disi/reli

(15)

显然,如果impi越大则表明特征越重要,故可以从多个备选特征中选取部分特征来进行训练。

虽然本文主要是使用RatioCut来进行谱聚类,但考虑到信息资产安全基线的特点,需要尽量减少误报,故提出平均差异度指标(Average difference index,ADI)对聚类结果进行评价,如式(16)所示

(16)

式中:E为数学期望即均值,W为两个样本点的相似度。

可以看出提出此指标是在原来的聚类结果中增加一个约束条件。ADI的值是小于1的,而且此值越小,则表明学习结果接受度越高。可以通过设置阈值对结果进行判断,若高于此阈值则拒绝,否则接受。另外,如果仅对样本点进行二分类,考虑到相关安全上下文,需要再增加一个指标,即负向样本数量和正向样本比值,这个值越低越好,一般最好在0.1以下,称之为簇比例指标(Clusters proportion index,CPI),可以将ADI和CPI的乘积作为聚类结果是否接受的评判标准。

3 实验过程与分析

在信息资产行为检测中,异常数据的获取是比较困难的。在验证的环境中,使用Malfease网站提供相关恶意软件,背景流量使用某高校在一段时间采样的pcap包,规模为TB级,包括服务器区中的约30余台主机在若干天的分时段网络通信。实验环境中使用Cuckoo沙箱部分模拟这些服务器的IP地址及其通信行为,然后获取其网络数据包以便进行混合回放。

本文相关实验主要采用两种信息资产行为异常场景:其一为内网主机连接外网行为;其二是内网主机连接内网其他主机行为。

经过综合比对和筛选,选取如下特征分别作为谱聚类数据向量:

(1)内网连接外网。TCP标志比例、平均包长、平均会话包数、数据入出度之比、DNS会话比例、ICMP会话比例、DNS解析失败比例、HTTP连接异常比例、加密会话比例、连接境外地址比例、非常见端口连接比例。

(2)内网互连。总体数据吞吐、平均包长、平均会话包数、数据入出度之比、非常见端口连接比例、敏感端口访问比例、访问端口数、访问服务器比例、访问终端比例。

上述特征的选取主要考虑一些恶意软件的相关网络行为,如泛洪攻击、端口尝试、隐蔽通道通信、横向扩散、傀儡行为等,故特征选取和具体相关业务存在天然的联系。

对于待检测数据,只要先进行特征抽取,再根据其与已分类数据的相似度的距离进行判断即可,即它距离哪种分类更近些。

3.1 实验过程

实验环境采用CentOS 6.9操作系统,CPU为Intel至强2650 v4,64 GB内存,网络接口为2块Intel i210千兆以太网卡,使用TcpReplay工具回放数据包。

表1所示为部分网络流量的主要协议分布统计情况。总的网络会话数量在3.55亿左右,表1中的数据约为总体的32%。从表1可以看出,主要协议还是DNS和HTTP,但还存在其他不能识别或者占比较少的其他网络流量。

表1 网络数据协议分布

表2所示为这些服务器中一台具有代表性的主机30天未加入恶意流量时的部分特征数据。其中,a1～a7分别表示平均包长、出入度比、DNS比例、DNS解析失败比例、加密比例、连接境外地址比例、非常见端口比例。平均包长和入出度比例未做标准化,可以使用MinMax方法进行归一化。

表2 服务器部分特征抽取(正常)

由于数据来源于服务器,故入出度比例是高于1的,而且对于未掺入恶意流量的数据而言,其连接境外和非常见端口相对比例偏低。

表3所示为其中3天中加入了一些恶意流量,包括木马、勒索、矿机等恶意流量后的部分特征抽取数据,从该表可以看出某些特征变化比较明显。

表3 服务器部分特征抽取(异常)

将此服务器的相关特征数据使用谱聚类算法进行二分类,分别按照未加入恶意流量和加入恶意流量的聚类结果进行观察,图1和图2给出了相关分类结果,其纵坐标为ADI×CPI,而横坐标为样本数量。

图1 ADI×CPI指标与样本数量关系(正常)

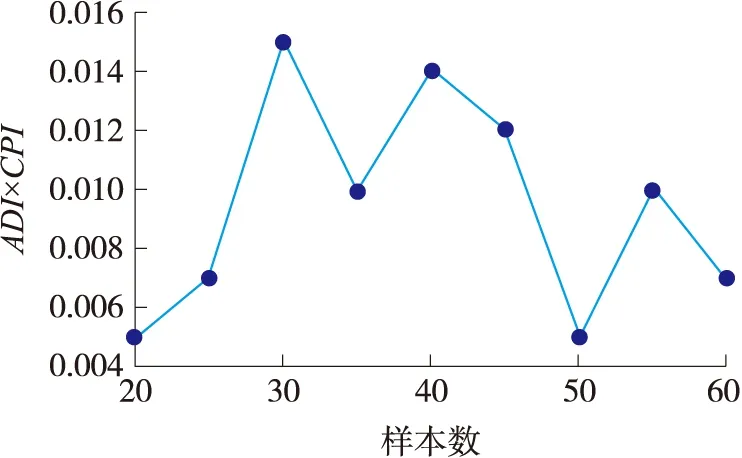
图2 ADI×CPI指标与样本数量关系(异常)

从图1和图2可以看出在加入了异常样本数据的分类结果后,ADI×CPI更小,更应该被接受。据此可以设置接受分类结果基线为0.02,高于此值的分类结果则无法接受,否则可能导致过多的误报。

另外,为了验证本文的学习效果,将相同的数据直接使用K-means算法进行实验以便进行比对,准确率和误报率结果分别如表4和表5所示。其中,对于表4而言,b1～b5分别是样本总数(天数)、异常样本数、全特征K-means聚类准确率、3个特征K-means聚类准确率、本文谱聚类算法准确率;表4用图展示,则显示如图3所示的效果。对于表5而言,c1～c5分别是样本总数(天数)、异常样本数、全特征K-means聚类误报率、3个特征K-means聚类误报率、本文谱聚类算法误报率。

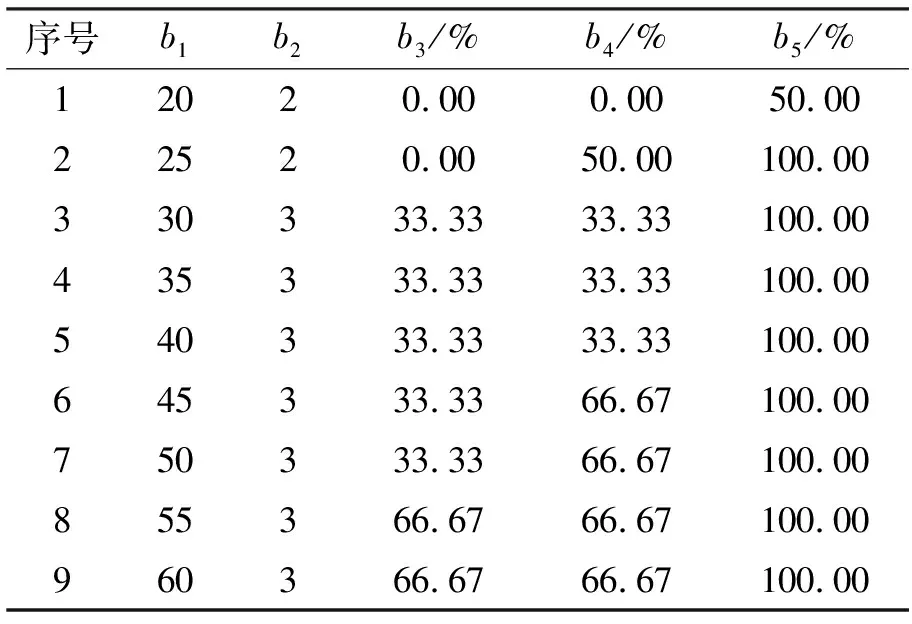
表4 K-means与本文方法比对(准确率)

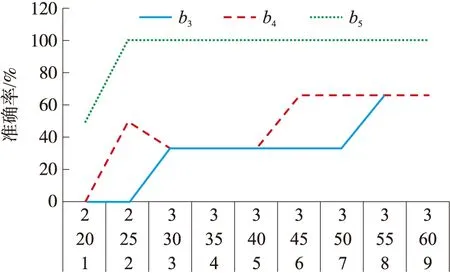
图3 K-means与本文方法比对(准确率)(注:谱聚类算法使用ADI×CPI=0.02)

表5 K-means与本文方法比对(误报率)

3.2 实验分析

从表4和表5可以看出因为数据维度过高,即使使用了主成分分析(Principal component analysis,PCA)降维,其效果也不是特别理想,聚类准确率不高而误报率较高。原因是K-means在高维空间表现过于稀疏,无法在信息资产行为异常分类模型中使用,而本文的谱聚类方法表现良好。

以上实验可以看出在无监督条件下,使用基于谱聚类的机器学习方法可以产生理想的效果,能够对一些恶意软件产生的流量信息比较清晰地进行分拣和聚类。

通过表4和表5可以计算获得相关样本的准确率和误报分析,如表6所示。

表6 实验数据比对分析

使用本文谱聚类的方法对于检测的准确率有较大提升,误报率也急剧下降。当然,对于信息资产的异常行为检测本身就是一个非常复杂的系统工程。本文实验主要抽取的特征都是能够反映一些异常流量的性质。但从实验中可以看出,个别特征对于聚类结果可能并不敏感,例如平均包长度;而某些特征则比较敏感,如连接境外的地址、非常用端口等。这些现象取决于具体的信息安全检测上下文,主要包括以下4点:

(1)检查异常网络连接的方向,即应该区分训练数据的方向;

(2)是否需要检查基于洪水方式的攻击;

(3)是否需要检查异常模式的连接,包括大量连接、非正常时间、非正常地理位置、非正常源地址、非正常目的地址、非正常目的端口、非正常应用协议等的连接;

(4)是否需要检查隐蔽连接,隐蔽连接往往和IP、TCP/UDP以及应用层协议如DNS、HTTP等关联。

另外,由于安全问题的检测是一个变化发展的过程,故行为基线包括聚类的结果也是动态过程,必须保持一定频度的在线训练,不过需要注意的是在数据说服力不够的情况下宁可不生成行为基线。

4 结束语

本文利用基于谱聚类的机器学习算法对相关信息资产可能存在的异常行为,给出了相关结果接受指标,同时得到了良好的检测效果。今后将计划从如下几个方面继续探索方法和演进模型:(1)综合网络连接数据和主机运行数据,对可能的异常行为进行深度检测,包括创建/销毁进程、权限提升、防御绕过等无法从网络数据中获取的内容;(2)在不同检测方面对信息资产建立不同的行为基线;(3)研究和丰富动态行为基线模型,以达到更好、更高效地检测未知威胁的目的。总之,利用各类机器学习算法对信息资产的安全问题进行检测是一个值得研究和深入的领域,需要更多的方法和更为可靠的数据方可展开,研究目标则是更全面地发现问题和更准确地定位问题。