面向少数类用户兴趣演化的推荐算法

张 维,黄 勃,2,张 娟,高永彬,刘 瑾,王忠震

(1.上海工程技术大学 电子电气工程学院,上海 201620;2.江西省经济犯罪侦查与防控技术协同创新中心,江西 南昌 330000)

信息化技术的快速发展沉淀了海量的数据,加快了信息过滤技术的发展。推荐算法是信息过滤技术之一,它能够自动过滤与目标用户无关或用户不感兴趣的数据。基于模型的推荐、基于协同过滤的推荐和基于内容的推荐是主要的推荐算法[1]。其中,协同过滤算法应用最为广泛[2],但传统协同过滤算法也存在着许多挑战,例如用户和项目的冷启动挑战、数据稀疏的挑战和算法可扩展的挑战。同时,以往的研究发现,长久推荐用户感兴趣的内容,会使用户处在自己的信息茧房[3]之中。大量用户处于一种被自己兴趣所包围的环境,其认知、兴趣趋于窄化,形成一种认知屏障,失去认知和发现新事物的机会。为了能够一定程度的缓解信息茧房对用户所带来的负面影响,文献[4]提出了个性化算法优化、平台优化、改进信息供给侧的理论方法。文献[5]提出破除信息茧房所带来的“个人回音室”、“群体极化”等影响个人和社会的负面效应,需要从“个性化推荐”转变为“人性化推荐”。目前,在推荐算法的研究中,很少考虑信息茧房负效应对用户影响,特别是少数类用户。少数类用户是近邻用户数量很少的一类用户,当对这类用户进行推荐时,如果不采取措施对用户数量进行平衡,将会使其兴趣窄化,陷入信息茧房之中。

在传统的协同过滤算法中,没有考虑信息茧房效应的发生。文献[6]利用加权Slope One(Weighted slope one,WSO)算法对稀疏评分矩阵进行填充,通过聚类算法对填充后的矩阵进行用户聚类,缩小目标用户搜索最近邻的时间,提高了算法扩展性。文献[7]通过对用户-项目矩阵进行分析,采用K-means聚类算法把兴趣偏好相似程度较高的用户划分到同一簇中,减少了推荐时用户搜索最近邻的时间。上述的聚类算法对用户进行聚类,提高了推荐的准确度,但是随机的聚类中心,会造成用户的近邻不稳定,影响推荐的质量。而且没有对聚类结果中的少数类用户进行分析与深入考虑,很容易使这类用户受困于信息茧房。

以往大量的实验研究表明,将用户偏好因素考虑到算法中,能有效提高推荐的性能。Zhang等[8]提出一种将用户偏好聚类的协同过滤算法,算法通过用户对项目类型的平均评分构造用户偏好矩阵,并与用户-项目矩阵合并,然后使用WSO算法填充评分数据中的未评分项。王明佳等[9]提出了一种将用户的显式偏好和隐式偏好相融合的推荐算法,通过用户评分抽象出用户对项目的隐含偏好,最后将各个用户在隐式和显式偏好上的相似度加权。上述的算法能够反映出用户的兴趣偏好,提高推荐的准确度,但是忽略了时间对于用户兴趣的影响,用户兴趣随时间的变化对用户推荐的准确度的影响很大。而且一味地探索用户感兴趣的项目,不采取应对信息茧房负效应的措施,不仅使少数类用户受困于信息茧房,而且会加剧这个问题。

基于以上分析,本文提出一种面向少数类用户兴趣演化的推荐算法,不仅提高对少数类用户进行推荐的准确性,而且避免信息茧房负效应产生。首先,本文利用用户对项目类型的评分时间不同和评分的不同得到相应的时间因子,将其融入到用户对项目类型的偏好之中,并对兴趣独特或者兴趣接触面小的用户采用兴趣均值方式来缓解其兴趣稀疏问题。然后,利用均值的方式计算用户对项目类型的兴趣,通过计算用户对项目各类型的兴趣均值,结合项目评分均值和用户自身评分均值来表示用户的评分倾向,对未评分项进行预测,并填充到对应的未评分项中。最后通过改进的K-means聚类算法对具有不同兴趣倾向的用户进行聚类,并对类簇中近邻数量少的用户(少数类用户)进行平衡处理,增加近邻数量。

1 相关工作

1.1 用户相似度计算

在推荐算法中,衡量用户之间相似程度的方式通常是相似度计算。它能够描述两个同维度向量之间的相似程度。常用的相似度计算方式[10]包括余弦相似度计算、改进的余弦相似度计算、皮尔逊相关系数计算。皮尔逊相关系数的计算方式如式(1)所示

(1)

1.2 评分预测

评分预测是推荐算法中对用户进行预测推荐的一种有效方式[11]。通过评分预测可以预测出用户潜在的兴趣关注点。计算公式如式(2)所示

(2)

式中:sim(u,v) 表示用户u、v之间的相似程度;Nu表示用户u的最近邻集合;|sim(u,v)|表示相似用户数。

1.3 优化初始聚类中心的K-means聚类算法

聚类是一种无监督学习,能够根据规则自动将数据分成若干类,在同一类中的数据对象之间的相似度高于在不同类中的数据对象之间的相似度。K-means算法采用欧式距离来度量数据对象之间的相似度,欧式距离d(x,y)计算方法如式(3)所示

(3)

式中:n表示数据对象的维度,d(x,y)的值越小表示数据对象之间的相似度越高。K-means算法虽然核心思想简明、容易实现,但是也存在许多局限性。例如算法中的K值仅凭经验来选取,很难找到最优值;初始聚类的中心点选取不当,会导致聚类效果不稳定。

针对以上问题,文献提出了改进初始聚类中心的K-means聚类算法[11]。算法通过在数据空间分布上找到不同密度内的K个点作为初始聚类中心。假设有数据集D,每个数据对象维度为n。改进初始聚类中心的K-means聚类算法步骤如表1所示。

表1 改进初始聚类中心的K-means聚类算法

2 少数类用户的兴趣演化及其兴趣平衡

本文提出的面向少数类用户兴趣演化的推荐算法由4个关键组成。

(1)解决原评分矩阵数据稀疏的问题。通过用户对项目的显式行为把用户对项目属性的隐式偏好抽象出来,得到用户项目类型矩阵,然后以用户对各项目类型的兴趣均值来填充原评分矩阵中未评分项。

(2)捕捉用户随时间演化的兴趣。利用用户对事物遗忘的周期规律、兴趣稳定的时间窗口以及与项目的交互频率得到用户对不同项目类型的时间衰减因子,并与用户项目类型矩阵融合,刻画出不同用户兴趣演化的不同规律。

(3)解决少数类用户数过少的问题。通过改进的K-means算法对兴趣演化后的用户进行聚类,聚类结果中存在用户数量极少的用户。将以少数类的簇心为圆心,离其簇心最远的用户的距离为半径的圆作为少数类用户的边界。把包含在边界内的多数类用户以有放回采样的方式纳入少数类,并逐渐增大边界,直到少数类用户数达到各类簇中用户数的平均水平,从而达到平衡少数类用户数量的效果。

(4)生成目标用户的推荐。将用户数据预处理后的用户评分矩阵与聚类得到的用户近邻结合,并利用协同过滤算法来预测目标用户对项目的评分,选取预测评分值最高的N个项目推荐给用户。

本文的算法整体框架图如图1所示。

图1 推荐算法的整体框架图

2.1 数据预处理

在传统协同过滤算法中,用户对项目的共同评分项目数对算法的性能影响很大。项目交集越多,算法的效果越好。实际上,用户之间的项目交集很小。但是,可以根据用户的显式行为推测出用户所隐含的偏好。比如用户u1看过电影“复仇者联盟”和“雷神”,并给出了不错的评价,而用户u2看过“蜘蛛侠”和“绿巨人”,同样也给出了不错的评分。因为这4部电影类型很相似,都具有动作、喜剧等元素,两个用户都表达出喜爱的态度。因此,从用户隐式偏好的角度出发,提取出用户之间更多的交互数据,提高推荐效果。

从用户的对项目的评分(显式行为)可以计算出用户对项目类型(隐式行为)的评分。对于用户u已评分的项目集合Iu,每个项目i具有多个类别Tt,用户u对项目类别Tt平均评分为Rut,计算公式如式(4)所示

(4)

式中:it的值为1或者0,值为1表示项目i具有类型Tt,值为0表示项目i不含类型Tt;numt表示用户u已评分项目具有的类别总数。

为了解决用户-项目矩阵中数据稀疏的问题,本文对用户-项目矩阵进行预处理。通过式(4)可以得到用户对项目类型的均值偏好,通过均值偏好可以近似填充用户未评分的项目,数据填充方式如式(5)所示

(5)

(6)

2.2 时间因子影响的用户兴趣

在给用户推荐信息的时候,如果不考虑用户的兴趣随时间变化就会导致推荐信息不准确[12]。例如小时候喜欢看动画片的人群,在成长的过程中,可能由喜欢动画片到爱情片再到科幻片。每个时期的兴趣关注点都可能发生变化,一方面可能来自年龄的变化,对电影的关注点有所差异,另一方面则是因为身边人群的兴趣不同,逐渐去关注身边环境中其他人的兴趣,存在着从众心理。但也会因为个人此刻的心情,而出现短暂式的兴趣关注点,就像刚刚度过疲劳期的用户,就倾向于关注轻松愉快的主题。

有文献表明,人的兴趣演化是一种普遍现象,变化的趋向也各有不同。易受外界影响的兴趣往往是比较短暂的,用户更深层次的兴趣才能经受时间考验(即在很长一段时间内,对某几个类型电影的关注度丝毫没有减弱)。例如很多经历过战争年代的人,很容易关注抗战题材的电影,这种题材的质量高低、上映时间,都不会影响其关注。与其说兴趣促使这类用户关注这类型电影,不如说情怀使他时刻关注。因此,在考虑影响用户兴趣演化的核心要素时,除了考虑用户兴趣值随时间衰减,还应当考虑兴趣值稳定时间和交互行为。

文献[13]提出了一种融入时间窗口的指数衰减函数,利用时间窗口来稳定一段时间内用户对项目类型的兴趣值。本文提出一种改进融入时间窗口的指数衰减函数算法,让用户兴趣受时间窗口和用户项目交互信息共同影响,其计算方式如式(7)所示

(7)

利用式(4)得到的时间权重,融入到用户对项目类型的兴趣中,可以描述出用户随时间变化的兴趣值。并且根据用户与项目类型的接触频率和接触时间,能够表示出用户对该项目类型不同时间段的兴趣值。用户随时间推移的最终兴趣数值如式(8)所示

(8)

式中:Nt表示用户评价同一项目类型Tt的次数;Put表示用户对项目类型Tt的喜好程度,随着接触项目类型的次数多了,受时间的影响就越小;t表示项目类型总数;rutj表示第j次对该项目类型的评分。用户项目类型矩阵是以用户和项目类型为行列标识、Put为元素的矩阵。

2.3 少数类用户的兴趣平衡

通过改进的K-means算法对融合用户深层次兴趣的用户项目类型矩阵进行用户聚类。聚类得到的类簇中有大量近邻数量的类簇,也有很少的近邻数量的类簇。邻居数量少的类簇中的用户称为少数类用户。对于少数类用户,其近邻太少,最直接的影响就是在对其推荐的时候推荐选择项少。选择项是用户是否会产生信息茧房负效应的最重要的判断依据。选择项过少,这类用户就会被禁锢在个性化推荐的信息茧房中,整个少数类用户中的其他用户也会产生类似的效应,不仅仅是产生群体极化现象,而且是产生信息茧房负效应的群体极化,这样会将一类人群禁锢在同一信息茧房之中。因此,为了避免此情况的产生,在进行推荐之前再平衡数据集。

不平衡数据集是指数据集中的不同类别样本数量极度不平衡,这与本文使用改进的K-means算法得到的聚类结果中类簇用户数量不平衡极其相似。在对用户进行推荐时,近邻数量多的用户在达到一定的近邻用户数的时候其推荐准确度趋于稳定,但这并不表示,其余的近邻就不会影响其推荐准确度。推荐是多元化信息的结合,呈动态化的,所以下一时间段对目标用户产生重要影响的可能是其他的近邻。近邻数量多的用户,不仅少有可能困于信息茧房,还可适应多元化世界的变化。而近邻数量少的用户则不同,近邻数量过少,直接会导致推荐的选择项少和信息茧房现象的产生。多数类用户和少数类用户之间是有一定联系的,他们之间存在兴趣面交叉的现象,例如少数类用户感兴趣的项目类型就几个,而多数类用户中存在对少数类用户感兴趣的项目类型感兴趣的用户,所以将这类存在在多数类用户中的与少数类用户有交叉兴趣面的用户作为少数类用户的增添邻居最为合适。平衡少数类用户的算法如表2所示,少数类中用户数的平衡过程如图2所示。

表2 平衡少数类用户的算法

在预测评分时,当预测用户存在于多个类中,选取该用户到各类中心点距离最小的类,将该类中的用户作为近邻。如图2所示,具有相同形状的图形属于同一类簇,少数类1和少数类2按照上表的规则扩大自身的边界,将融入边界的多数类用户作为自己的扩展近邻,该近邻用户不会从多数类中移除,只是复制给少数类用户,帮助少数类拓展兴趣面的同时提高对其推荐的准确性。

图2 少数类中用户数的平衡过程

2.4 算法描述

本文算法在得到用户近邻平衡化结果和预处理的矩阵后,利用传统协同过滤算法对目标用户进行推荐。如式(1)所示,通过近邻用户和预处理后的矩阵,得到近邻用户之间的相似度。如式(2)所示,利用目标用户与近邻的相似度以及用户的平均评分来预测出目标用户对项目的评分,然后选取评分最高的N个物品给目标用户推荐。本文的推荐算法描述如表3所示。

表3 面向少数类用户兴趣演化的推荐算法

3 实验及结果分析

3.1 实验数据集

本文数据集来自GroupLens研究小组创建的电影评分数据集。该数据集包含了若干规模大小不一的数据集。本文使用了MovieLens 100K的数据集进行算法性能试验。该数据集包含了1 943名用户对电影的评分,评分值范围是1～5之间的整数。每个电影可能包含多个电影类型。本实验把数据集按照均匀分布随机分成N组,其中N取10,挑选一组作为测试集,其余的数据作为训练集。为保证评测指标不是过拟合或者误差的结果,进行了N次交叉实验,并以N次实验所得评测指标的平均值作为最终的评测标准。

3.2 评价指标

本文采用平均绝对误差(Mean absolute error,MAE)和均方根误差(Root mean square error,RMSE)作为评价本文算法性能的指标。MAE和RMSE的值越小,预测误差就越小。计算公式分别如式(9)和式(10)所示

(9)

(10)

式中:用户u对项目i的真实评分为rui,rui={ru1,ru2,ru3,…,run};用户u对项目i的预测评分值为r′ui,r′ui={r′u1,r′u2,r′u3,…,r′un}。

3.3 实验结果与分析

本文首先对实验所涉及到的参数进行讨论,需要的参数有3个,分别为:影响到改进K-means算法的初始聚类中心和用户聚类数的占比率α;反映兴趣稳定时间窗口的参数Tw;表示用户兴趣衰减权重的ω。

实验1通过占比率α=0.15和MAE的最小值来确定参数Tw值。占比率α=0.15是由改进K-means算法中得到的最优参数。如图3所示,当ω=1/50,Tw=8时,得到最小MAE值;当ω=1/60,Tw=7时,得到最小MAE值;当ω=1/70,Tw=7时,得到最小MAE值。由此可知,当Tw=7时,最小MAE值样本较多,所以本文算法选择Tw=7作为标准,表示一周内用户兴趣不发生变化。

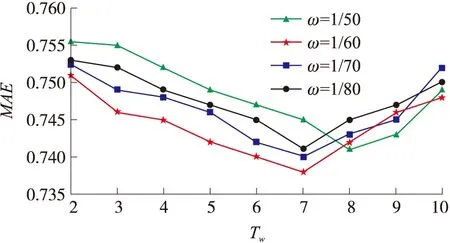
图3 不同参数Tw和参数ω对应的MAE值趋势图

实验2由稳定时间窗口Tw和MAE的最小值来确定参数ω的值。当Tw=7时,通过改变ω的值来推出Tw和ω的最优组合,将ω的值分别设置为1/10、1/20、1/30、1/40、1/50、1/60、1/70、1/80,如图4所示。当Tw=7,ω=1/60时,MAE值最优。由此,本文算法设置Tw取值为7,ω取值为1/60。

图4 不同ω值对应的MAE值趋势图

实验3本文算法与基于用户的协同过滤算法(UCF)[14]、基于K-means算法的协同过滤算法(KMUCF)[15]、基于用户聚类和稀疏矩阵填充的推荐算法(CFUCF)[16]进行了对比与分析,由此表明本文算法在基于用户的协同过滤算法基础上所做的改进工作比UCF、KMUCF和CFUCF 3个算法得到的推荐效果好。为了比较各算法的MAE和RMSE稳定值大小的差异,设置最近邻个数从25递增到45,递增间隔为5。表4描述了MAE和RMSE的值随用户最近邻个数逐渐趋于稳定时的变化,N表示最近邻个数。由表可知,本文算法相对于UCF算法的MAE值降低了2.07%,相对于KMUCF算法的MAE值降低了0.95%,相对于CFUCF算法的MAE值降低了0.14%。在RMSE评价标准上本文算法最好,相对于UCF算法降低了2.74%,相对于KMUCF算法降低了1.44%,相对于CFUCF算法降低了0.34%。

表4 MAE和RMSE值的变化

图5反映了最近邻个数的变化对MAE和RMSE值的影响,实验设置最近邻个数从5递增到45,递增间隔为5。由实验可知,MAE和RMSE的值慢慢趋于稳定状态,而且在不同的最近邻个数下,本算法得出的MAE和RMSE值都明显比其他算法的MAE和RMSE值低,且当最近邻个数为30时,各算法的MAE和RMSE值都趋于稳定。由此说明本文算法在考虑用户行为和时间因素影响的兴趣演化时会得到更好的效果。

图5 算法的MAE和RMSE值的趋势图

4 结束语

本文的算法针对传统算法中忽略推荐的时效性而影响推荐的准确性、用户可能受困于信息茧房和聚类中心不稳定导致的用户邻居不稳定等问题,提出一种面向少数类用户兴趣演化的推荐算法。利用时间因子和用户行为频率分析用户深层次兴趣,通过优化初始聚类中心的K-means聚类算法对深层次兴趣相似的用户聚类,使得用户邻居极其稳定。采用平衡数据集方法将少数类用户与多数类用户关联,生成更多少数类用户的最近邻集合,提高少数类用户的推荐人性化。通过实验可知,本文的算法与传统算法比较明显提升了推荐的准确度,同时也避免少数类用户受困于信息茧房之中,使得算法面向的人群更加宽广,更富有人性化。本文主要研究用户与项目之间因交互而产生的隐含关系,但用户的属性和项目的属性本身存在内在的联系。因此,后期需通过客观事实和规律来捕捉用户兴趣与项目之间的关系,提高推荐的准确性。