非负Tucker分解的随机方差缩减乘性更新算法

白姗姗,史加荣

(西安建筑科技大学 理学院,陕西 西安 710055)

非负矩阵分解(Non-negative matrix factorization,NMF)将非负数据表示为非负基下的非负线性组合,已被广泛应用于图像处理、文本数据挖掘等诸多领域[1,2]。面对结构更加复杂的高维数据,若仍运用NMF方法将待研究的数据向量化,将会导致局部数据信息缺失,破坏数据的空间几何结构[3]。为此,Welling等[4]提出了具有更高数据压缩性能的非负张量分解。

现有的张量分解一般分为两类:标准分解/平行因子分解(CANDECOMP/PARAFAC,CP分解)和Tucker分解[5]。这两种分解模型分别可看作奇异值分解(Single value decomposition,SVD)和主成分分析(Principle component analysis,PCA)的高阶推广,并且CP分解是Tucker分解模型的特例。非负Tucker分解(Non-negative Tucker decomposition,NTD)将高维非负张量分解为一个低维非负核心张量与一系列非负模式矩阵的模式积[6]。NTD使模型具有较强的可解释性,近年来受到很大关注,已成功应用于计算机视觉[7]与信号处理[8]等领域。

Kim等[9]最先引入NTD的乘性更新(Multiplicative update,MU)算法,Hazan等[10]提出了具有梯度思想的MU算法。尽管现有的算法取得了较好的效果,但它们收敛速度较慢,尤其不适用于高维数据。随着深度学习的迅速兴起,随机梯度下降算法(Stochastic gradient descent,SGD)已成为求解大规模机器学习优化问题的主流方法[11-14]。该算法具有参数更新过程简单、收敛速度快且计算复杂度低等特点。尽管SGD具有许多吸引人的特性,但到目前为止,尚未见到将该算法扩展到非负Tucker分解模型的研究。因此,本文基于随机梯度下降思想提出了求解非负Tucker分解的一种新算法:随机方差缩减乘性更新(Stochastic variance reduced multiplicative update for NTD,SVRMU_NTD)。该算法将随机方差缩减梯度和乘性更新规则相结合,对非负的高维数据进行Tucker分解,可在提高张量分解性能的同时降低计算复杂度。

1 非负Tucker分解

X=G×1A(1)×2A(2)×3…×NA(N)

(1)

则称这种分解为Tucker分解。其中,Jn≤In,“×n”表示张量的n-模矩阵积,定义为

(2)

核心张量G可看作是张量X的压缩版本。在一般情况下,分解后的张量存储空间会比原来的张量小很多。图1给出了一个三阶张量Tucker分解的示意图。

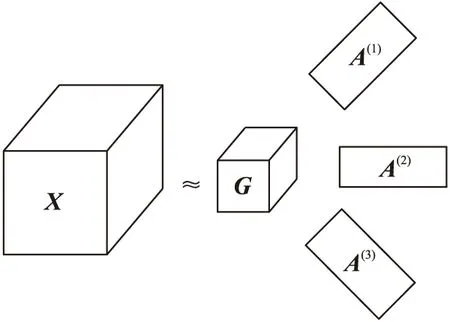
图1 三阶张量的Tucker分解示意图

使用欧氏距离来度量张量X分解的逼近程度,即NTD对应的最优化模型见式(3)。

(3)

式中:‖·‖F表示张量的Frobenius范数,称(J1,J2,…,JN)为多重线性秩。求解式(3)的算法有很多,例如交替最小二乘法(Alternate least squares,ALS)[15],列坐标下降(Column coordinate descent,CCD)[16],高阶乘性更新(High order multiplicative update,HONMF)[17]等。但这些算法迭代效率较低且计算复杂度较高,不适用于求解高维张量分解问题。

2 求解NTD的随机方差缩减乘性更新算法

2.1 非负Tucker分解的乘性迭代算法

在最优化模型(见式(3))的目标函数中,将X进行n-模式化,有

(4)

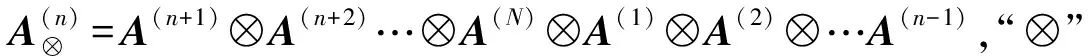
与NMF的乘性迭代算法类似,文献[18]提出了求解优化模型(见式(3))的MU算法,其主要更新过程如下。模式矩阵A(n)的更新形式为

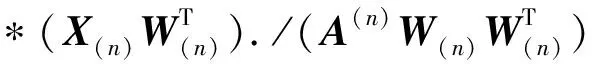
(5)

核心张量G的更新公式为

G←G.*(X×1(A(1))T…×N(A(N))T./

(G×1(A(1))TA(1)…×N(A(N))TA(N))

(6)

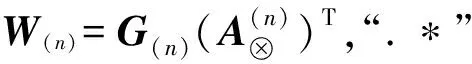
2.2 随机方差缩减乘性更新算法

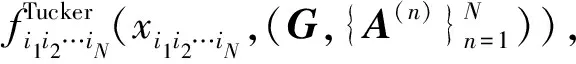
随机方差缩减梯度算法(Stochastic variance reduction gradient,SVRG)[19]是在SGD的基础上添加了方差缩减技巧,具有双层循环结构。在外部循环中,参数经过若干次内循环之后会保留一个“快照点”,然后需要计算损失函数在该点处全体样本的平均梯度,从而加快了参数的迭代速率。本文基于SVRG提出一种新的求解非负Tucker分解的随机方差缩减乘性更新算法SVRMU_NTD,其基本迭代过程如下。

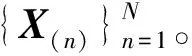
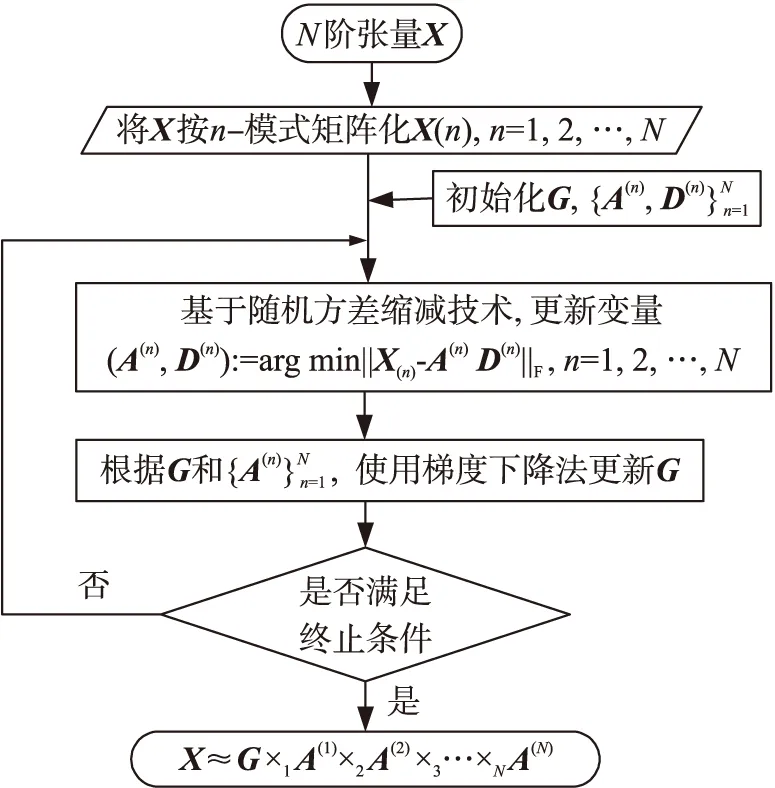
图2 SVRMU_NTD的非负Tucker分解流程

2.2.1 模式矩阵的计算

(7)

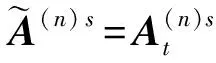
(8)

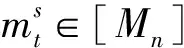
(9)

基于式(9),更新参数第n个模式矩阵

(10)

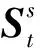
(11)

(12)

根据如下形式来更新步长矩阵

(13)

式中:αs为外循环第s次中随迭代次数的增加而不断缩减的学习率,即

αs+1=ραs,ρ∈(0,1)

(14)

2.2.2 核心张量的计算

一旦获得N个模式矩阵{A(n)},可运用梯度下降法来更新核心张量G。根据模型(3)得核心张量的梯度为

X×1(A(1))T…×N(A(N))T

(15)

迭代步长T按照以下形式选取

T=(λG)./(G×1(A(1))TA(1)…×N(A(N))TA(N))

(16)

式中:λ∈(0,1)表示更新核心张量的学习率。当λ=1时,对应NTD算法中G的更新公式。因此,核心张量的更新规则为

G←G-T.*(Gf)

(17)

算法的更新过程如算法1所示。

算法1非负Tucker分解的随机方差缩减乘性更新算法(SVRMU_NTD)

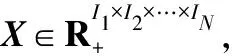
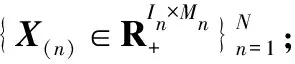
3: Fors=0,1,…,do

5: Fort=1,2,…, do

6: Forn=1:N

12: End

13: End

14: 根据式(14)更新αs;

17: 根据式(16)更新迭代步长T;

18: 根据式(17)更新核心张量G;

19:End

3 数值实验

将SVRMU_NTD算法在人工合成数据集、高速公路交通视频数据集和COVID-CT图像集上进行实验,并与传统的NTD算法和简单版本的随机乘性更新(Stochastic multiplicative update for NTD,SMU_NTD)算法进行性能比较。

3.1 实验设置

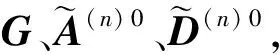
给定非负张量X,它的重构张量为X′,使用相对误差来评价它的逼近性能

(18)

相对误差越小,逼近性能就越好。

3.2 人工合成数据集

图3 人工合成数据集迭代效率和时间效率对比

图3(a)中,横坐标表示全局迭代次数,纵坐标表示相对误差。从图3(a)可看出:在第20次迭代时,NTD、SMU_NTD和SVRMU_NTD算法的相对误差分别为0.438 3、0.214 2和0.021 5。NTD算法的迭代效率较低,难以在有限的迭代次数内逼近最优解,这可能是因为NTD只使用了MU规则,更新过程简单且计算复杂度较高。作为随机梯度简单版本的SMU_NTD算法,其迭代效率略强于NTD,采用了随机梯度与乘性更新相结合,提高了分解性能。SVRMU_NTD算法迭代效率最高,先运用方差缩减乘性更新来进行非负矩阵分解,得到模式矩阵集;再通过梯度下降思想来更新核心张量,使其能够在较少的迭代次数内逼近最优解,有效地提升了算法性能。

图3(b)对比了3种算法的时间效率,其中:横坐标表示运行时间,纵坐标表示相对误差。在最大迭代时间0.5 s内,这3种算法相对误差随迭代次数的增加而呈现出的变化趋势。由图3(b)可见,NTD算法很快达到某局部最优解之后,尽管随着时间的增加相对误差仍保持不变,算法性能最低。SMU_NTD算法的时间效率稍微强于NTD,但明显低于SVRMU_NTD算法。虽然SVRMU_NTD算法初始迭代较慢,但随着时间的增加相对误差迅速降低,一直保持下降趋势,能够高效、快速逼近目标参数的最优解。

3.3 交通视频数据集

该段视频数据集来自于华盛顿州交通部(https://www.wsdot.wa.gov/)。由254个西雅图高速公路交通视频序列组成,共有44个连续的交通高峰(慢速或停驶速度),45个中等交通流量(减速),165个轻交通流量(正常速度)。每个视频的分辨率为320像素×240像素,每秒10帧,每个序列的大小为48像素×48像素。最后,为了减少不同照明条件的影响,对每个视频片段减去均值图像,将像素强度归一化为单位方差。本文选取第100个属于正常速度的高速公路交通视频序列,该图像集可表示为48×48×51的张量,部分图像如图4所示。

图4 高速公路交通视频的部分图像

从图5(a)可知:在有限的迭代次数内,NTD、SMU_NTD和SVRMU_NTD这3种算法的最终相对误差分别为0.329 4、0.209 8和0.137 3。NTD到达某一局部最优解之后,相对误差几乎不再变化,其迭代效率最低。SMU_NTD算法引入了随机思想,虽加快了迭代效率,但很难在较少的迭代次数内逼近最优解。而SVRMU_NTD算法保留了随机方差缩减的性质,在第二次迭代之后就接近局部最优解,算法性能最高。由于随机方差缩减梯度算法可逃离鞍点,不断地寻找更优的局部最优解,故相对误差随迭代次数的增加而不断减少。

图5(b)比较了3种算法的时间效率。可看出:在迭代时间为0.5 s内,这3种算法相对误差随迭代次数的增加而变化的趋势。NTD算法在0.5 s内迭代了214次,但相对误差却是0.320 3,这是由于自身单层循环结构相对简单,只运用了MU规则,故迭代效率最低,在0.1 s后,尽管不断地迭代其相对误差几乎保持不变。SMU_NTD在一定程度上提升了NTD的优化效率,但时间效率较低于SVRMU_NTD算法,要使其达到最优解还需更长的时间进行迭代。SVRMU_NTD算法在相同时间内只迭代了39次,但相对误差却达到0.137 7,具有非常强的矩阵分解性能,因为该算法结合了“方差缩减”策略和乘性更新规则来校正梯度估计量,使其能够稳定、快速地逼近最优解。与其他两种算法相比,SVRMU_NTD算法在迭代效率与时间效率上都具有明显优势。

图5 高速公路交通视频数据集迭代效率和时间效率对比

为不失一般性,考虑对核心张量维数的不同选取进行实验,通过改变(J1,J2,J3)的取值来判断SVRMU_NTD算法的有效性。在集合{(5,5,8),(8,8,10),(10,10,12)}中来选取(J1,J2,J3),比较不同取值下算法的迭代效率,实验结果如图6所示。

由图6实验结果可知:(J1,J2,J3)在3种不同取值下SVRMU_NTD算法的最终相对误差依次为0.357 1、0.252 6和0.145 2,运行时间依次为0.254 3 s、0.275 9 s和0.278 8 s。在不同核心张量维数下,按(0,1)区间上的均匀分布随机初始化核心张量G,故初始相对误差随核心张量维数的增加而降低。可见,在有限的迭代次数内,相对误差随核心张量维数的不断增加而减小,但时间也会随之增长。对于较少的迭代次数,较小的核心张量维数对应的相对误差快速下降,之后趋于平缓;而较大的核心张量维数对应的相对误差一直保持下降趋势,迭代效率较高。因此,若将SVRMU_NTD算法应用于高维复杂数据,需考虑选取合适的核心张量维数,使其在时间相对短的情况下,迭代效率能达到相对最优,从而使张量分解更加准确、高效。

图6 核心张量不同维数下的相对误差

3.4 COVID-CT图像集

为了更加说明所提算法的应用价值,对COVID-19 CT数据进行测试,比较以上3种算法的实际性能。该数据集是关于COVID-19最大的公开可用的CT图像数据集[20],其中包含来自216名患者的349张COVID-19阳性CT图像和397张COVID-19阴性CT图像。本文选取COVID-19阳性CT图像的前200幅扫描图像,每幅图像大小调整为180×180。因此,该数据张量的维数为180×180×200。部分原始图像如图7所示。

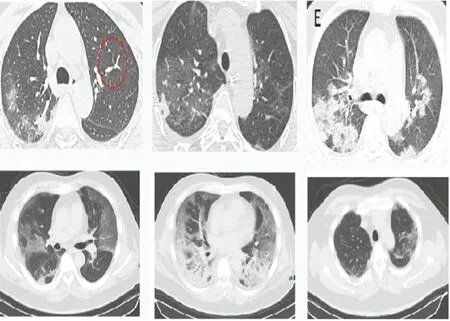
图7 部分阳性CT图像

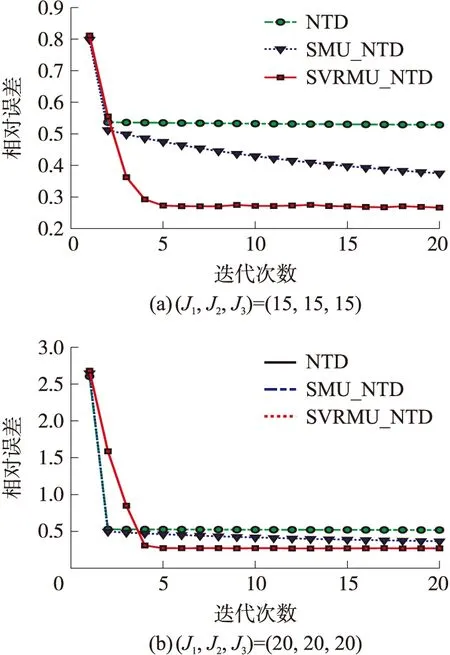
图8 不同核心张量维数下对COVID-CT图像集的迭代效率对比

图8(a)和图8(b)分别表示核心张量维数为(15,15,15)和(20,20,20)的情况下,3种算法的相对误差随迭代次数的增加而变化的趋势。从图8可见:各算法的实际性能大体趋势与交通视频数据集基本保持一致。SVRMU_NTD算法性能明显优于其他两种对比算法,相对误差随迭代次数的增加而迅速减小,当(J1,J2,J3)=(20,20,20)时,相对误差已达到0.233 7,这说明该算法张量分解结果更加准确。同时可看出,核心张量维数越大,初始相对误差越低,且能够在有限的迭代次数内快速逼近最优解。

图9展示了不同核心张量维数下,3种算法的时间效率对比。由图9(a)和图9(b)可知:NTD算法极易陷入局部最优解,随着迭代次数的增加相对误差却几乎不再变化。相比其他两种算法,SVRMU_NTD算法的性能最强,在相同迭代时间3 s内,相对误差达到最小,能够在极少的迭代次数内快速逼近最优解。以核心张量维数(J1,J2,J3)=(20,20,20)为例,在运行时间3 s内,NTD算法迭代了298次,相对误差为0.503 8,SMU_NTD算法迭代了122次,相对误差为0.348 3,而SVRMU_NTD算法仅迭代了24次,相对误差却达到0.267 0。可见,SVRMU_NTD算法在迭代效率以及时间效率上都占有一定的优势。但总体而言,核心张量维数越大,初始相对误差越小且所需时间也相应延迟,故在实际应用中需针对不同的数据选取合适的核心张量维数,使其在迭代效率和时间效率上都能够达到相对最优。

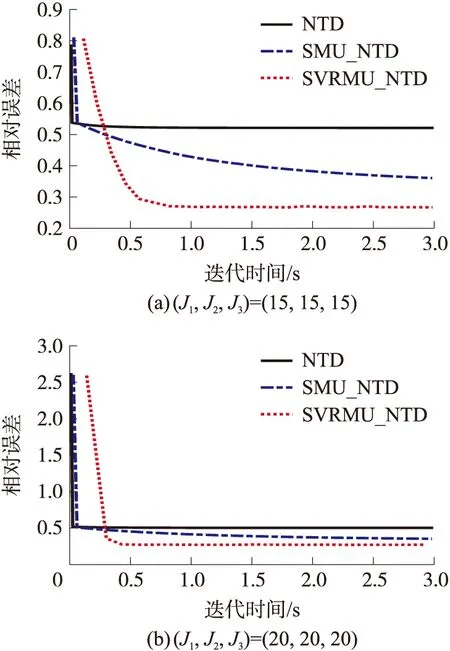
图9 不同核心张量维数下对COVID-CT图像集的时间效率对比

4 结束语

本文提出了求解非负Tucker分解的随机方差缩减乘性更新算法。此算法先将待分解的数据张量n-模式化,然后结合随机方差缩减策略和乘性更新规则对模式化矩阵进行非负分解,得到模式矩阵,最后利用梯度下降思想对核心张量进行更新。实验结果表明,与传统的NTD以及SMU_NTD算法相比,本文提出的算法加快了收敛速度且降低了计算复杂度,具有更好的数据张量分解效果,也适用于大规模并行计算。离线情况下,本文提出的算法具有计算代价较高、存储空间较大等缺点,如何运用在线的随机梯度下降算法来求解非负Tucker分解问题将是未来值得研究的问题。