拱形-线形非线性磁力耦合压电俘能器建模与特性分析

陈孝玉，张旭辉，左 萌，樊红卫，汪 林

(1.西安科技大学 机械工程学院，西安 710054；2.陕西省矿山机电装备智能监测重点实验室，西安 710054;3.遵义师范学院 工学院，贵州 遵义 563006)

近十年来，能量收集技术受到了学术界与工程界广泛的关注[1]。基于压电效应的振动能量收集技术具有能量密度高、体积小、便于与电路集成等优点，有望解决便携式设备、无线传感节点等微电子设备自供电问题，已成为当前研究热点[2]。

为实现能量转换，悬臂直梁式压电俘能器由于结构简单、制造方便等优点被广泛应用于能量收集。为提高能量收集性能，大量研究对直梁结构进行了优化与设计。Erturk等[3]设计了一种L型梁，研究表明这种L型梁具有2阶接近的谐振频率，相对于传统直梁，可以拓宽工作频带；Yang等[4]提出了一种拱形结构梁，仿真表明拱形结构具有更大、均匀的应力分布，相对于直梁，拱形结构梁有更高的电压输出和能量转换效率，且双拱形结构梁能量转换效率最高；Cao等[5]设计了一种具有2种不同厚度截面的梁，研究结果表明其峰值输出电压与功率分别是传统直梁的1.69和1.8倍，尤其适用于低频环境；Wang等[6]设计了一种截面厚度变化的悬臂梁，通过有限元仿真表明，受力时梁表面应变较传统直梁更大、更均匀，均匀的应变有利于减小压电材料电荷流动能量的耗散，实验表明这种梁可以较直梁提高78%能量收集效率。

以上研究表明通过结构优化可以改善俘能器俘能性能。为拓宽俘能器工作频带，进一步提高能量收集效率，在悬臂梁结构中引入磁力非线性以拓频受到广泛研究。Erturk等[7]通过实验证明了磁力耦合非线性可以引起双稳态高能阱间振动，从而提高能量收集器收集性能；在简谐激励条件下，Zhou等[8]验证了双稳态压电俘能器的多解范围与宽频特性；张旭辉等[9]设计了一种复合梁式双稳态振动能量收集器，实验表明磁力耦合作用下俘能器有效带宽是无磁力作用下带宽的3.1倍；Zhao等[10]在随机激励条件下，通过比较分析证明了双稳态能量收集器性能优于单稳态收集器；Fang等[11]在脉冲激励条件下，证明具有磁力耦合双稳态特性的能量收集装置较线性结构可以提高22.9%的功率输出。

以上研究表明改善悬臂梁结构与构建双稳态俘能器均有助于提高压电俘能器能量收集性能，而当前的双稳态压电俘能器研究仍多采用直梁结构，为此，设计了基于拱形-线形梁结构磁力耦合双稳态能量采集器。利用广义扩展Hamilton原理建立了其动力学模型,揭示不同磁距、激励条件等对能量采集器振动特性影响关系并进行验证，最后通过实验验证了拱形-线形结构较直梁结构俘能器的优越性。

1 结构模型

1.1 拱形-线形压电俘能器结构

拱形-线形压电俘能器总体结构如图1所示，其主要由基座、拱形-线形悬臂梁、磁块A与磁块B、压电材料(PVDF)所构成。不同于传统直梁式压电悬臂梁，拱形-线形压电俘能器采用半径R的圆弧状曲梁与直梁组合结构。压电俘能器总体呈拱形-线形状，压电材料粘贴于悬臂梁拱形部分表面，悬臂梁自由端磁块B与固定于基座磁块A保持磁力相斥关系。悬臂梁在上下振动过程中，受曲梁结构曲率变化的影响，会产生非线性恢复力，同时，磁块A与磁块B适当间距会使系统呈双稳态特性，这将有利于拓宽压电俘能器有效工作频带，提高俘能性能。

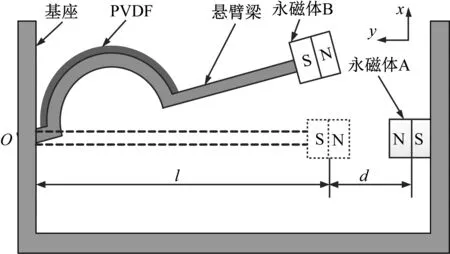
图1 拱形-线形压电俘能器结构图Fig.1 Structural diagram of the ALEH

1.2 数学建模

为建立拱形-线形压电俘能器力-电-磁耦合动力学模型，本文采用广义Hamilton变分原理

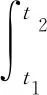
(1)

式中:δ为变分符号;Tk为压电俘能器系统动能;U为系统势能;We为压电材料(PVDF)电能;Wnc为系统非保守力虚功;Um为两磁铁间磁力势能。

系统动能Tk可以表示为

Tk=T1+T2+T3

(2)

式中：T1表示拱形-线性压电俘能器金属基体层动能;T2表示压电片动能;T3表示自由端磁铁质量块B动能。故相应表达式如下

(3)

式中:u(x,t)为悬臂梁横向位移;Vp、Vs分别为压电层体积与金属基体层体积;m0为磁铁质量块B质量。根据压电材料能量转换方式及本构方程，压电材料电能We可表示为

(4)

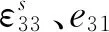
系统非保守力虚功Wnc的变分δWnc可表示为

(5)

式中:m(x)为单位长度悬臂梁质量;z(t)为基座位移;Q为压电元件表面电荷;v为有效电压。

为建立拱形-线形压电悬臂梁振动微分方程，应用Rayleigh-Ritz法将梁的横向相对位移u(x,t)展开为离散形式

(6)

式中:i表示压电悬臂梁的振动模态阶数;φi(x)表示拱形-线形梁第i阶弯曲模态振型函数;ri(t)表示第i个广义模态坐标。由于拱形-线形压电俘能器主要低频、低幅环境振动能量的收集，其结构响应主要为一阶模态，二阶及以上模态的影响可以忽略。故仅考虑组合梁一阶模态变形，这里，采用一端夹紧，一端自由悬臂梁容许函数近似拱形-线形梁一阶振型函数[12]，故有：

(7)

结合以上等式，根据Euler-Bernoulli梁理论，Kirchhoff’s定律，拱形-线形压电悬臂梁振动微分方程可表示为

(8)

(9)

式中：M为模态质量;C为模态阻尼;θ为机电耦合系数;Cp为压电元件电容。其可以分别表示为

(10)

(11)

(12)

(13)

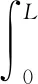
(14)

式中,Frr、Fmr分别表示模态坐标下拱形-线形压电悬臂梁自身结构非线性恢复力及由磁力引入产生的非线性磁力，将在下节讨论确定。

1.2.1 磁力计算

准确的计算拱形-线形压电俘能器中非线性磁力大小对于分析其振动特性尤为关键，当前对于非线性磁力的计算多采用磁偶极子法。磁偶极子法忽略磁块尺寸对位姿的影响，将其看作一对磁偶点进行建模，该方法在两磁块间距相对于磁块自身尺寸较大的场合可以获得较好的建模精度，而当间距较小时，其计算结果与实际有较大误差，Wang等[13]以实验证明了该结论。介于文中两磁块磁距间隔较小、且需要调节距离。为获得准确磁力模型，考虑磁块尺寸对偏转位置关系的影响，采用磁化电流法计算磁块间磁力大小。磁化电流法理论依据为经典的电磁理论，其认为导磁材料在磁场中受到的力可归结为分子电流所受的力，但由于磁场在导磁材料中分布复杂，直接采用该理论计算磁力比较困难，这里假定磁场在导磁材料区域中分布均匀，磁块A、B空间位置示意图如图2所示。

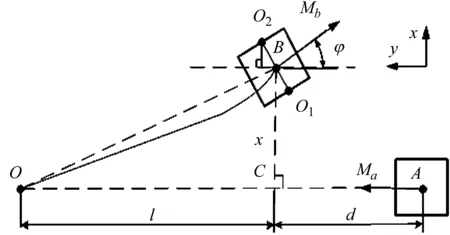
图2 磁力模型Fig.2 Magnetic field model

设磁块A、B磁化强度大小分别为Ma,Mb,其长、宽、高分别为la、wa、ha及lb、wb、hb，悬臂梁长度为，以磁块A中心为坐标原点建立坐标系，其磁化强度沿y方向，根据磁化电流理论，则其在空间中任意坐标点(x,y,z)处沿y轴产生的磁场强度可表示为[14]

(15)

其中：

(16)

(17)

则磁块B受磁块A产生沿x方向的磁力大小可表示为[15]

Fx=μ0MbS(Hy1-Hy2)

(18)

式中:μ0表示真空磁导率;S表示磁块B的上(或下)表面面积;Hy1和Hy2分别表示磁块A在磁块B下表面和上表面中心处产生沿x轴方向上的磁场强度。

拱形-线形压电俘能器在振动过程中，磁块B沿x轴位置会不断发生改变，且角度会发生偏转，为确定磁块B的坐标，记磁块B下、上表面中心点分别为O1和O2，发生与水平方向呈φ角度的偏转，由于悬臂梁刚度较大，通常偏转角度较小，可认为∠φ=∠BOC，故可采用以下关系式确定O1和O2相应坐标，其分别为

(19)

(20)

则Fx可以表示为

(21)

由于磁化电流法磁力表达式较复杂，为便于动力学方程求解计算，采用多项式拟合方法将磁力Fm表示为关于位移u(L,t)的三次多项式，可得

Fm=c1u3(L,t)+c3u(L,t)

(22)

1.2.2 结构非线性恢复力的确定

拱形-线形压电俘能器采用了拱形与直梁组合结构，振动过程中，不同于直梁结构呈线性恢复力，其在振动时曲梁部分曲率半径会随着振动方向的改变而发生变化，继而产生自身结构非线性恢复力。

为确定拱形-线形压电俘能器结构非线性恢复力，采用实验测量后数据拟合方式获取。将拱形-线形压电俘能器曲梁端固定于基座，测力计(型号YLK-10)缓慢推动自由端，并记录位移-恢复力数据，反复几次测定后取其平均值，然后采用多项式拟合位移-恢复力关系，可得如下拱形-线形压电俘能器结构非线性恢复力Fr与位移u(L,t)关系式

Fr=k1u3(L,t)+k2u2(L,t)+k3u(L,t)

(23)

式(23)中系数k1、k2、k3分别为29 186，-238，16。图3是实验数据拟合后拱形-线形压电俘能器结构非线性恢复力Fr与位移u(L,t)的关系曲线。从图3中可以看出，由于拱形-线形压电俘能器曲梁结构的存在，使得结构自身恢复力与位移不再是线性关系，而是非线性关系，同时，位移-恢复力曲线并不是对称曲线，说明俘能器在振动过程中正、反方向恢复力大小并不相同，这主要是由于振动方向改变导致曲梁曲率半径变化不对称所致。

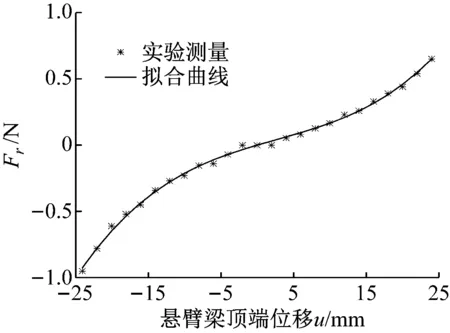
图3 拱形-线形压电俘能器非线性恢复力曲线Fig.3 The nonlinear restoring force curve of arc-linear beam

1.3 势能特性分析

结合以上分析，系统总势能可表示为

U=Ur-Um

(24)

式中:U为系统总势能;Ur为拱形-线形梁恢复力势能;Um为磁力势能。改变磁间距会影响磁力，从而影响拱形-线形压电俘能器特性，不同磁距下系统总势能图如图4所示，由图可知，随着磁距的减小，会形成2个明显的势阱，构成双稳态压电俘能器。而随着距离的增大，势阱深度变浅，当磁距大于16 mm后系统接近于单稳态系统。继续增大磁距，超过18 mm后，磁力减弱，双稳态消失，拱形-线形压电俘能器退化非线性单稳态系统。故磁距d=16 mm时，系统呈双稳态特性，且具有低的势垒与势阱，这意味相对于其它磁力位置，这一磁距条件下系统大幅阱间振动所需能量更小。同时，从势能图可以看出，拱形-线形压电俘能器势能与传统双稳态压电俘能器形状并不相同，势能图呈左高右低非对称形状，这主要是由于拱形-线形结构梁非对称恢复力导致。

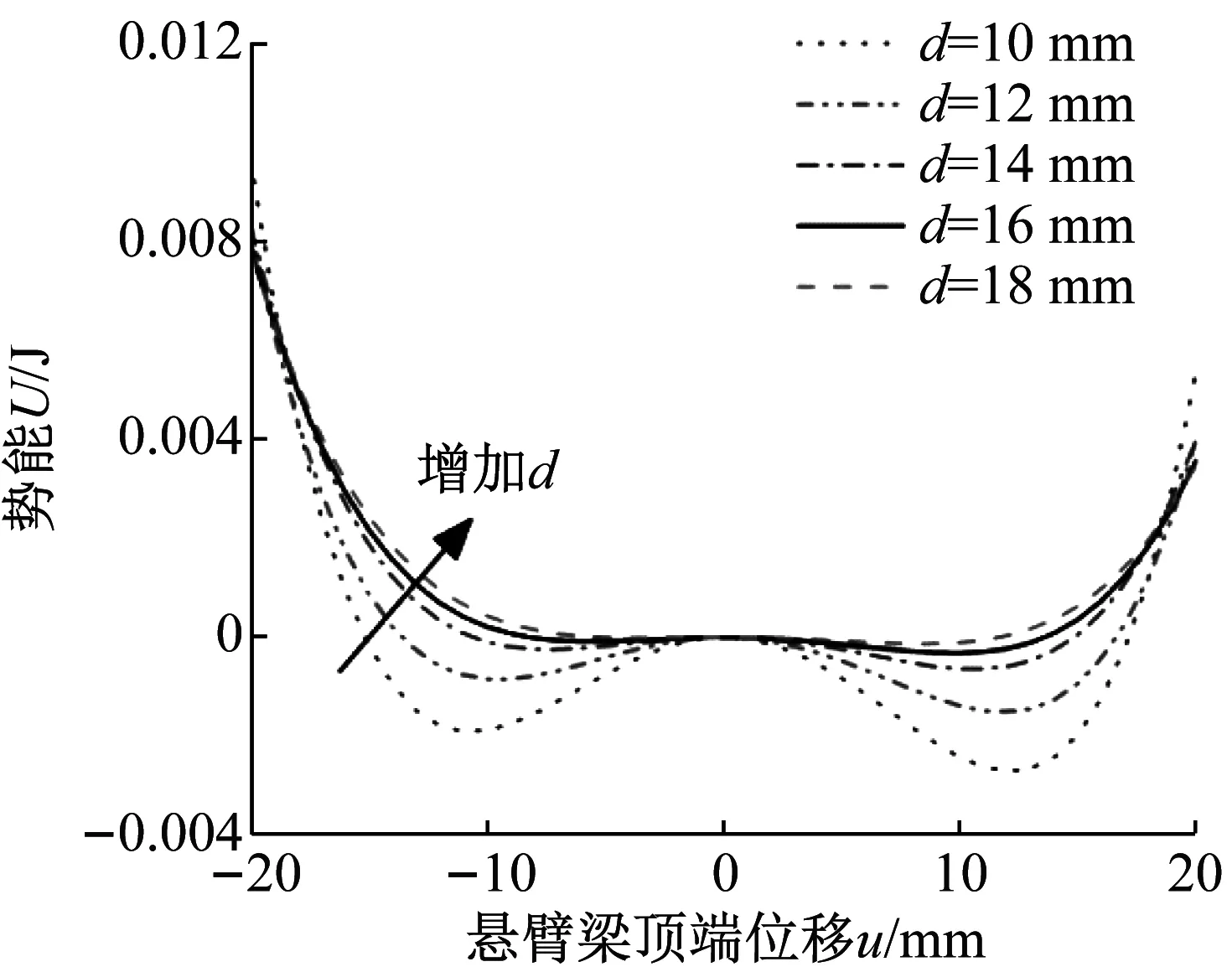
图4 不同磁距条件下系统势能曲线Fig.4 The potential curves of the system at different distances

2 静力学对比分析

目前压电俘能器研究中较多采用直梁为基体结构，直梁结构简单，易于制造，但存在刚度大，应力、应变分布不均等缺点，这将影响压电材料发电性能。为对比拱形-线形梁与直梁结构对压电材料力学性能的影响，分别选取长度为40 mm，宽度8 mm拱形-线形梁与直梁，材料为铍青铜，其中拱形-线形梁曲梁部分半径为10 mm，其余参数均与直梁保持一致。长度32 mm，宽8 mm压电材料(PVDF)，分别粘贴于拱形-线形梁曲梁部分与传统直梁固定侧表面。在其自由端施加0.5 N作用力，利用有限元软件ANSYS分别对其进行静力学分析，以对比同等作用力条件下，两种悬臂梁上压电材料(PVDF)表面应变关系。应变有限元计算结果如图5所示，对比图5(a)、(b)应变云图可以发现，拱形结构中PVDF总能在较多的区域保持高的应变值。两者应变值沿长度方向变化对比图如图6所示。

(a) 直梁结构PVDF应变分布图

从图6可以看出:压电材料最大应变均出现在固定端，直梁压电材料最大应变稍高于曲梁压电材料应变，前者沿长度方向呈线性急剧下降，这符合材料力学理论结果，最小值低于后者；由于拱形结构的影响，后者沿长度方向下降较为平缓，平均应变高于前者。这表明贴于拱形-线形梁上压电片平均应变更大，更加均匀。而大的平均应变有利于产生大的电压输出，均匀的应变可以减少压电材料电荷从高应变区向低应变区流动所需的能量消耗，有利于提高压电材料电压输出和能量转换效率[16]。故利用拱形-线形结构梁拱形特殊的应变分布有利于获得高的电压，提高俘能效率。

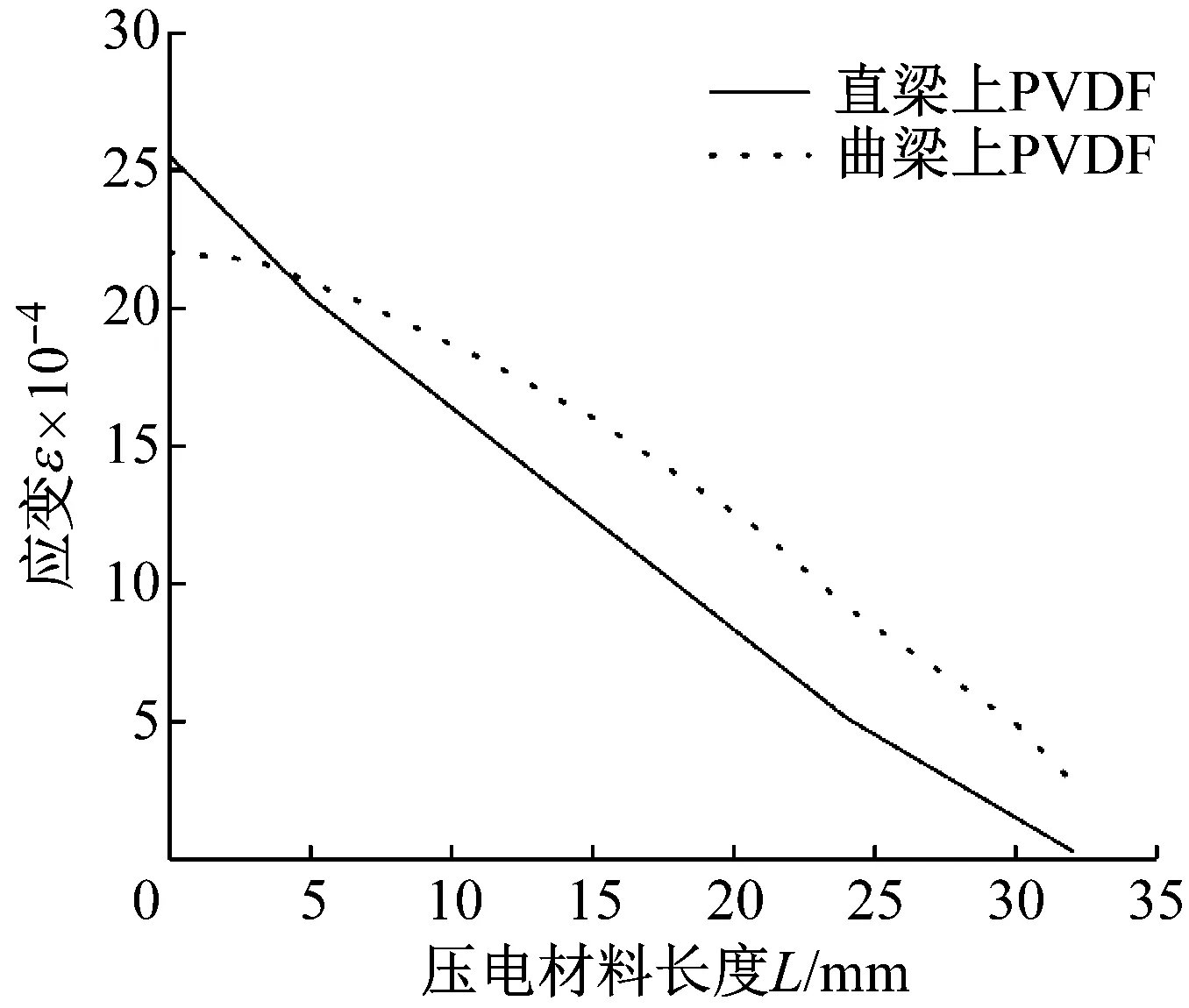
图6 拱形-线形梁与直梁上PVDF沿长度方向应变分布对比图Fig.6 Comparison of strain distribution of PVDF along length for the arc-linear beam and the straight beam

3 系统动力学分析

结合式(6)、(7)，可以由非线性磁力Fm与结构非线性恢复力Fr表达式，推导出模态坐标下压电俘能器末端磁力Fmr与非线性恢复力Frr表达式，代入动力学方程(8)中，即可得到拱形-线形非线性磁力耦合压电俘能器动力学方程，故动力学方程可表示为

(25)

(26)

r(t)=r0(t)+r1(t)sin(ωt)+r2(t)cos(ωt)

(27)

v(t)=v1(t)sin(ωt)+v2(t)cos(ωt)

(28)

式中，r0(t)表示系统的稳态平衡位置，r表示稳态位移幅值，其可以由下式确定

(29)

将式(27)、(28)代入系统动力学方程，令方程两边常数项、cos(ωt)及sin(ωt)系数相同，并忽略高次谐波项，可得以下等式

(30)

(k3-c3)r1-θv1=0

(31)

(k3-c3)r2-θv2=-HsA

(32)

(33)

(34)

在稳态响应时，以上式中所有关于时间导数项均为零，由此，稳态位移与电压响应可分别由式(35)、(36)计算确定。

(35)

(36)

谐波平衡解既包括稳定解，也含有不稳定解，稳定解可以在实验或数字仿真中实现，而不稳定解无法通过实验获取，稳定解判断可以通过系统动力学方程雅克比矩阵进行判断。

根据势能分析结果与上述求解分析，取磁间距d=16 mm，选择加速度幅值A=[0.5g,1.0g,1.5g]，分析不同激励条件对系统响应特性的影响关系。系统频响曲线如图7所示，其中图7(a)为不同激励强度下末端位移-频率响应曲线，图7(b)为不同激励强度下稳态电压(开路)-频率响应曲线。由于非线性动力学方程在一定频带范围，系统会出现多解特征，图中实线表示稳定解，虚线表示不稳定解。实现大幅阱间振荡最有利于提升发电性能，故主要针对系统大幅响应进行分析，图7(a)中位移r>8 mm时，系统作大幅阱间振动，相应地图7(b)中电压v>20 V时，系统作高能输出状态。对比图7(a)、7(b)可知，在同等激励强度下，系统大幅阱间振动位移与高能输出电压均随频率的增大而增大，系统大幅阱间振动与高能电压输出幅值与带宽变化规律具有一致性，即系统大幅阱间振动频带也即高能电压输出频带。这是由于系统大幅阱间振动时位移增大，致使拱形-线形悬臂梁变形增大，相应的压电材料形变变大，则产生大的电压输出。

由图7(a)不同激励强度下末端位移-频率响应曲线可知，当加速度幅值A=0.5g时，系统大幅阱间振动响应频率在7.2 Hz以下，其大幅响应位移最大值为11.3 mm，由图7(b)可知，相应的电压幅值约为29.4 V；当激励幅值为1.0g时，系统大幅阱间响应频率增至11.1 Hz，其大幅响应位移最大值增至15.4 mm，由图7(b)可知，相应的电压幅值约为37.8 V；进一步增大激励幅值至1.5g,系统大幅阱间响应频率增至14.2 Hz，其大幅响应位移最大值增至17.3 mm，由图7(b)可知，相应的开路电压幅值约为44.8 V；

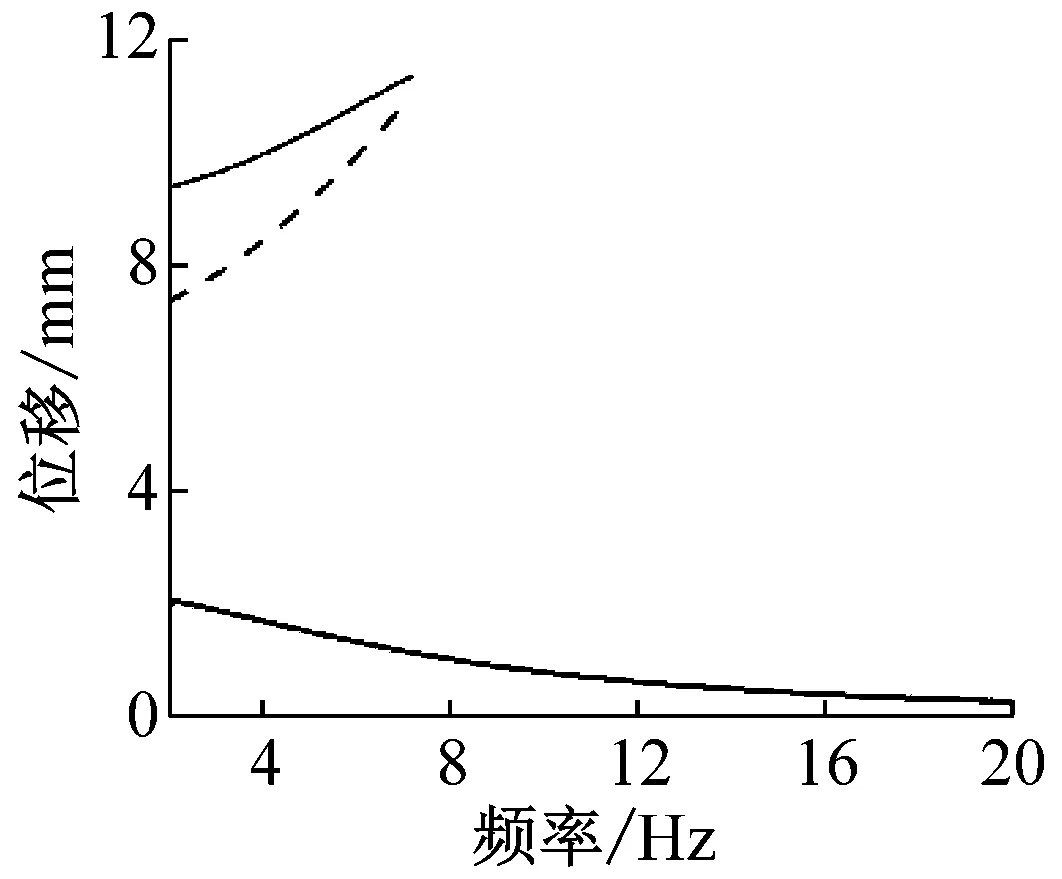
A=0.5g

从图7(a)中还可以看出，激励幅值不仅影响大幅阱间振动带宽与幅值，同时还影响小幅阱内振动带宽与幅值，当激励增至1.0g后，小幅阱内振动带宽变短，系统在低频出现稳定高能解；继续增大激励幅值至1.5g，小幅阱内振动带宽则进一步变窄，稳定高能解带宽由3.0 Hz增至5.8 Hz。随着激励频率增大，由于需要更大能量维持稳定高能解，在不增加激励幅值条件下，系统又处于高、低能量共存状态，直至无高能解。

从以上分析可知，外界激励水平是影响双稳态压电俘能器大幅响应带宽与幅值的重要因素。同时，由于磁距d的变化将影响非线性磁力的大小，会对系统响应特性构成影响。且磁距d便于调节，故掌握磁距变化对系统响应特性的影响关系具有重要工程价值。

取激励水平A=1.5g，选取不同磁距d=[12 mm,16 mm],研究同一激励水平下磁距变化对压电俘能器响应特性影响关系。不同磁距条件系统频率响应曲线图8所示，图8(a)为不同磁距条件位移-频率响应曲线；图8(b)为不同磁距条件稳态电压(开路)-频率响应曲线。由图8(a)可知，当磁距d=12 mm时，系统大幅响应带宽为15.2 Hz，位移幅值为16.4 mm，如图8(b)所示，此时相应电压输出幅值为42.1 V；当磁距增至16 mm后，由图8(a)可知，系统大幅响应带宽降至14.2 Hz，位移幅值为17.3 mm，如图8(b)所示，此时相应电压输出幅值为44.8 V；这表明系统磁距增加后，减小了拱形-线形双稳态压电俘能器大幅阱间振动带宽，但大幅振动位移幅值和稳态电压幅值有所增加。这主要是由于磁距增加后，磁力减弱，势阱变浅，在同一激励条件下，系统可能突破势阱限制，形成更大的振幅所致；而在小磁距作用下，系统难以突破两侧深的势阱形成更大的振幅。对比图8(a)、(b)不同磁距系统频率响应曲线还可以看出，磁距变化对大幅阱间振动轨道高度有着显著影响，磁距由12 mm增至16 mm后，大幅阱间振动轨道高度从13.5 mm降至10.6 mm，这是由于小的磁铁间距会产生大的非线性磁斥力，使势阱距离平衡点距离变远，拱形-线形双稳态压电俘能器势阱宽度变宽所致。

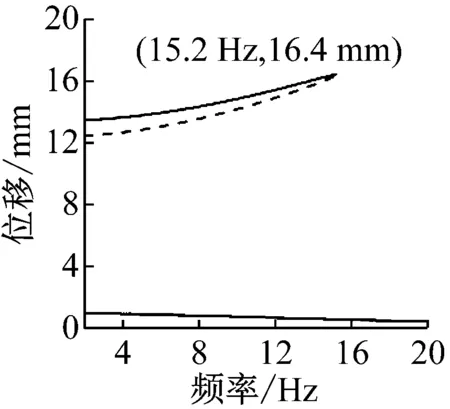
d=12 mm

以上表明磁间距对于拱形-线形双稳态压电俘能器响应特性有显著影响，适当减小磁距可以拓宽系统大幅响应频带，有利于增大系统平均输出电压。但过低的磁距会形成大的势垒高度，克服势垒则需要大的系统能量或外部作用力，从而在实际中难以实现双稳态大幅阱间振动。故磁距的选择需与外部激励水平及条件综合考虑确定。

进一步增大磁距，磁力减小，此时系统接近于无磁力状态，由于拱形-线形双稳态压电俘能器不同于线形直梁，由前述分析可知，其自身结构呈非线性恢复力，令动力学方程中c1、c3系数为零，改变不同激励条件，以分析拱形-线形压电俘能器结构非线性恢复力对频率响应曲线影响关系。无磁力条件下位移-频率响应曲线如图9所示，由图9可知，随着激励频率的增加，无磁力状态下的拱形-线形压电俘能器频响曲线向右倾斜，呈现硬特性，且随着激励强度增加，硬特性越明显。

图9 无磁力条件下系统频率响应曲线Fig.9 The frequency response curve of the system at nonmagnet condition

4 实验验证

为验证拱形-线形双稳态压电俘能器理论分析的正确性，搭建拱形-线形双稳态压电俘能器实验平台进行实验验证，实验装置如图10(a)所示，主要包括：计算机、主控制器、功率放大器、振动台、示波器、基座、拱形-线形压电能量采集器等组成。拱形-线形压电能量采集器由拱形-线形梁、压电薄膜PVDF及磁铁质量块(尺寸10 mm×10 mm×5 mm)组成。拱形半径10 mm，线形梁长度20 mm，宽度8 mm，厚度0.2 mm，梁材质为铍青铜，单层PVDF压电薄膜沿拱形-线形梁拱形部分贴合，PVDF长度为32 mm，宽度8 mm，厚度0.11 mm。为便于与传统直梁对比，制作长度40 mm直梁压电俘能器，其余参数值与拱形-线形压电能量采集器保持一致，两者结构如图10(b)所示。拱形-线形压电能量采集器一端固定于基座，另一端保持自由，自由端磁铁块与固定于基座永磁铁形成斥力关系，计算机与主控制相连用于信号控制与数据处理，信号发生器产生正弦信号，通过功率放大器激励振动台作正弦运动，能量采集器输出电压通过示波器采集获取，实验过程中，可以通过调节基座螺栓以改变两磁铁块间距离。

(a) 实验装置

首先调节磁铁间距d=16 mm，选取激励频率范围为10～20 Hz，分别选取激励水平为0.5g、1.0g、1.5g进行扫频实验，以验证不同激励条件对拱形-线形压电能量采集器响应特性的影响关系，拱形-线形压电能量采集器扫频输出电压如图11所示。

从图11可以看出，当激励水平A=0.5g时，系统未出现大幅响应输出；当激励水平A=1.0g时，系统高能电压输出幅值为34.3 V，大幅响应最大频率为13.2 Hz，相应仿真结果电压幅值为37.8 V，频率为11.1 Hz；当激励水平A=1.5g时，高能电压输出幅值为39.5 V，大幅响应最大频率为13.8 Hz，相应仿真结果电压幅值为44.8 V，频率为14.2 Hz。

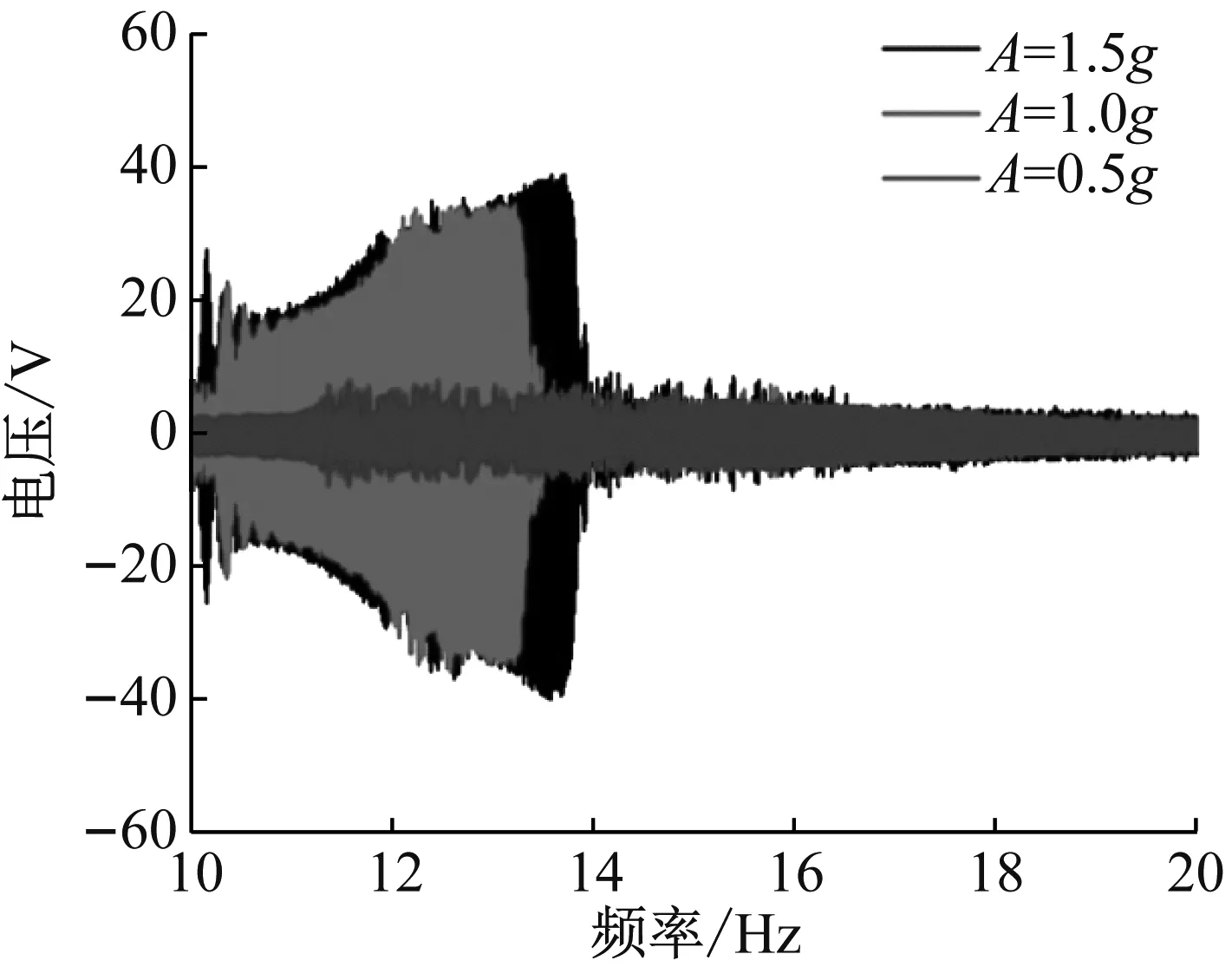
图11 不同激励强度下扫频电压输出图Fig.11 The sweep voltage diagram with different excitation intensity

实验结果表明：同一激励水平下，大幅响应电压输出随频率增大而增大；激励幅值增大，拱形-线形压电能量采集器高能输出电压带宽变宽，电压幅值随之增大,实验结果与理论分析结果定性吻合。

为验证不同磁间距对系统响应性能的影响，取激励水平A=1.5g，分别调节磁距d=12 mm与d=16 mm进行扫频(频率范围10～20 Hz)实验，不同磁距下能量采集器扫频电压输出如图12所示。

从图12中可以看出，电压输出随着激励频率的增大而逐渐增大。当磁距d=12 mm时，其电压输出幅值为35.2 V，相应仿真值为42.1 V；磁距增加至16 mm后，电压输出幅值为39.5 V，相应仿真值为44.8 V。实验表明：磁距增大后，电压输出幅值增大；同时，系统大幅响应的带宽有所减少。

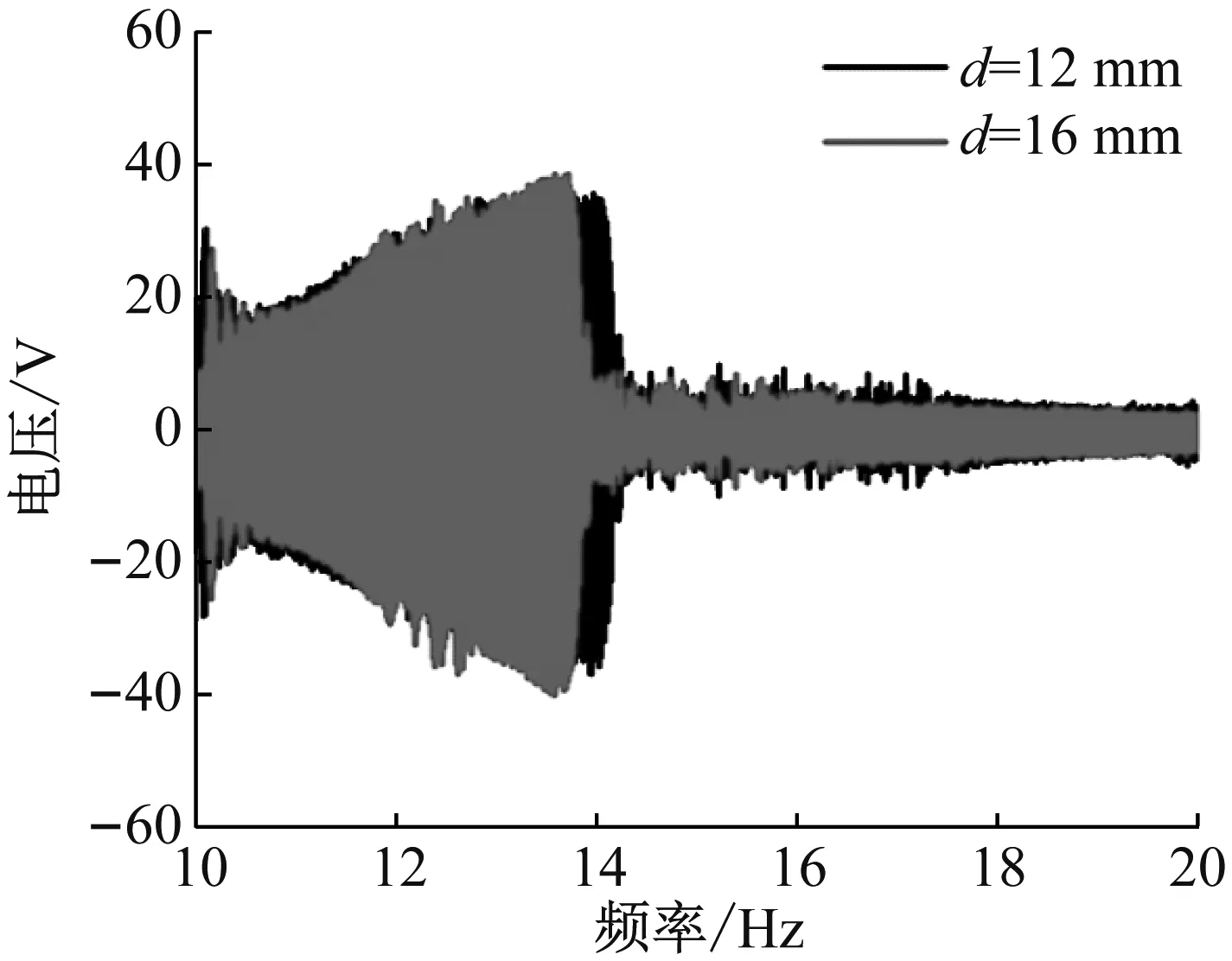
图12 不同磁距条件扫频电压输出图Fig.12 The sweep voltage diagram at different magnetic distance

以上实验结果与理论定性吻合，但定量上存在误差。误差主要由于拱形-线形梁振动过程中存在轴向变形，且相对于传统直梁轴向变形位移较大，这会影响磁铁间水平间距，使磁力理论计算与实际值间构成误差，从而影响模型预测精度；其次，压电材料与拱形部分间贴合材料与贴合状况也会对系统发电性能产生影响。

调节控制器输出信号，改变激励水平A=1.0g,对移除基座磁铁与有磁铁(d=16 mm)拱形-线形压电能量采集器进行扫频实验，以比较有、无磁铁对压电俘能器响应特性影响关系，系统扫频电压输出对比如图13所示，从图中可以看出，无磁铁时拱形-线形压电能量采集器大幅响应频带较窄，约为1 Hz，而施加磁力后压电俘能器大幅响应带宽变宽，约为3 Hz，这表明磁力耦合压电俘能器具有拓频作用。同时可以看出，无磁铁时拱形-线形压电俘能器峰值(谐振)电压曲线与传统直梁不一致，两侧明显不对称。左侧随着激励频率增大，电压输出逐渐增大，增至最大值约41.6 V后，急剧下降为10 V以下，这主要是由于拱形-线形压电俘能器非线性恢复力导致的硬特性所致。实验结果与无磁力条件下拱形-线形梁频率响应特性理论分析定性吻合。

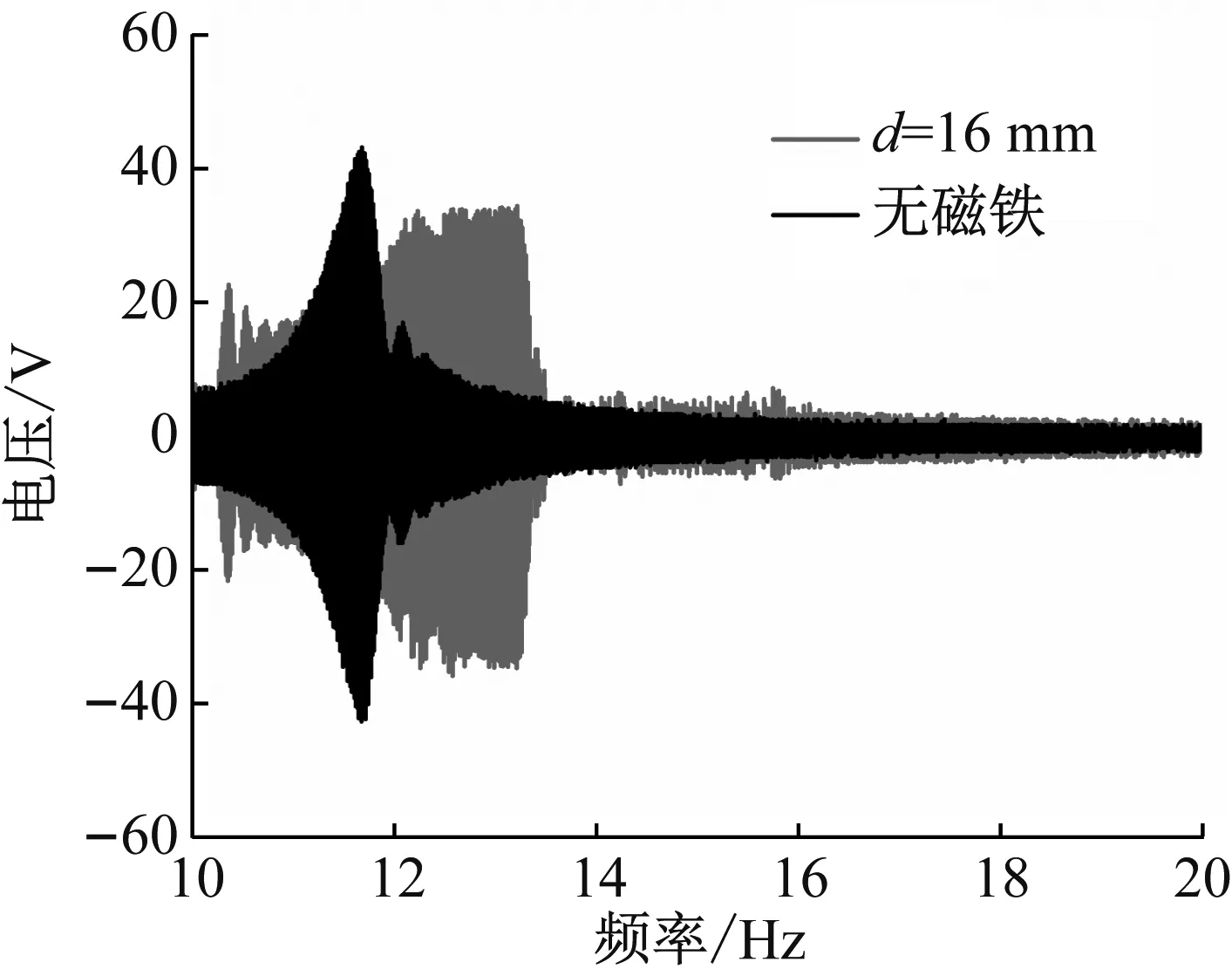
图13 磁力耦合与无磁铁系统扫频电压比较Fig.13 Comparison of frequency-swept output voltage between the ALEH and the non-magnetic system

为比较拱形-线形压电俘能器与传统直梁压电俘能器发电性能，选用直梁长度40 mm，PVDF长度32 mm，自由端质量块相同，在A=1.0g激励水平下执行扫频(10～20 Hz)实验。两者电压输出响应如图14所示，从图中可以看出，同等激励条件下，两者峰值电压分别为41.6 V、24.1 V，拱形-线形压电俘能器幅值电压约为直梁输出电压1.7倍，拱形-线形压电俘能器谐振频率约11.6 Hz，直梁约为17 Hz，这表明拱形-线形梁压电俘能器具有更低的谐振频率。

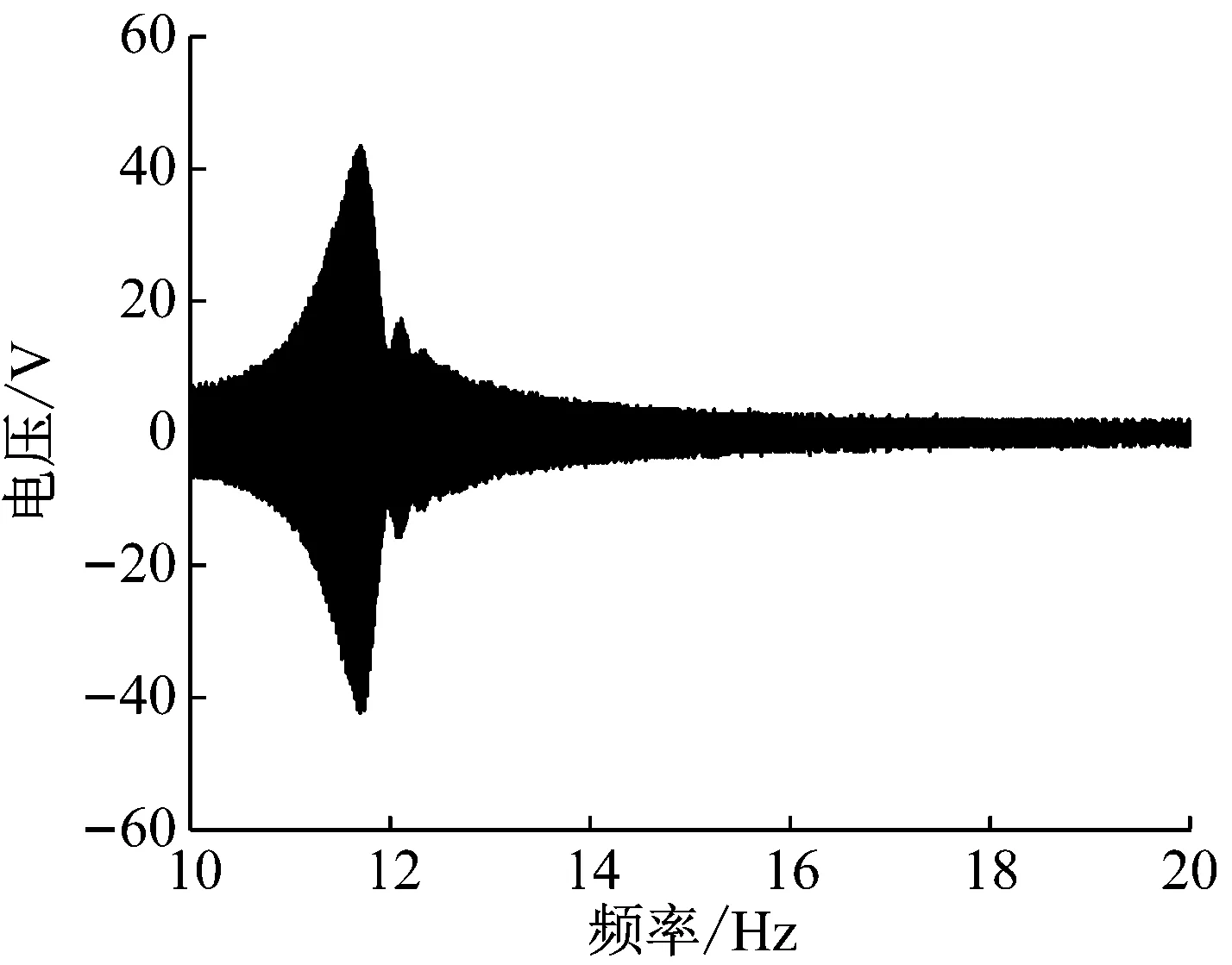
(a) 拱形-线形俘能器扫频电压

保持激励条件1.0g不改变，拱形-线形梁、直梁俘能器不同阻值条件下，在各自谐振频率处进行定频实验，其电压输出比较图如图15所示。从图中可以看出，在不同阻值条件下，拱形-线形压电俘能器电压输出曲线总位于传统直梁电压曲线上方，这表明同等外界条件下，拱形-线形压电俘能器输出电压总高于直梁。

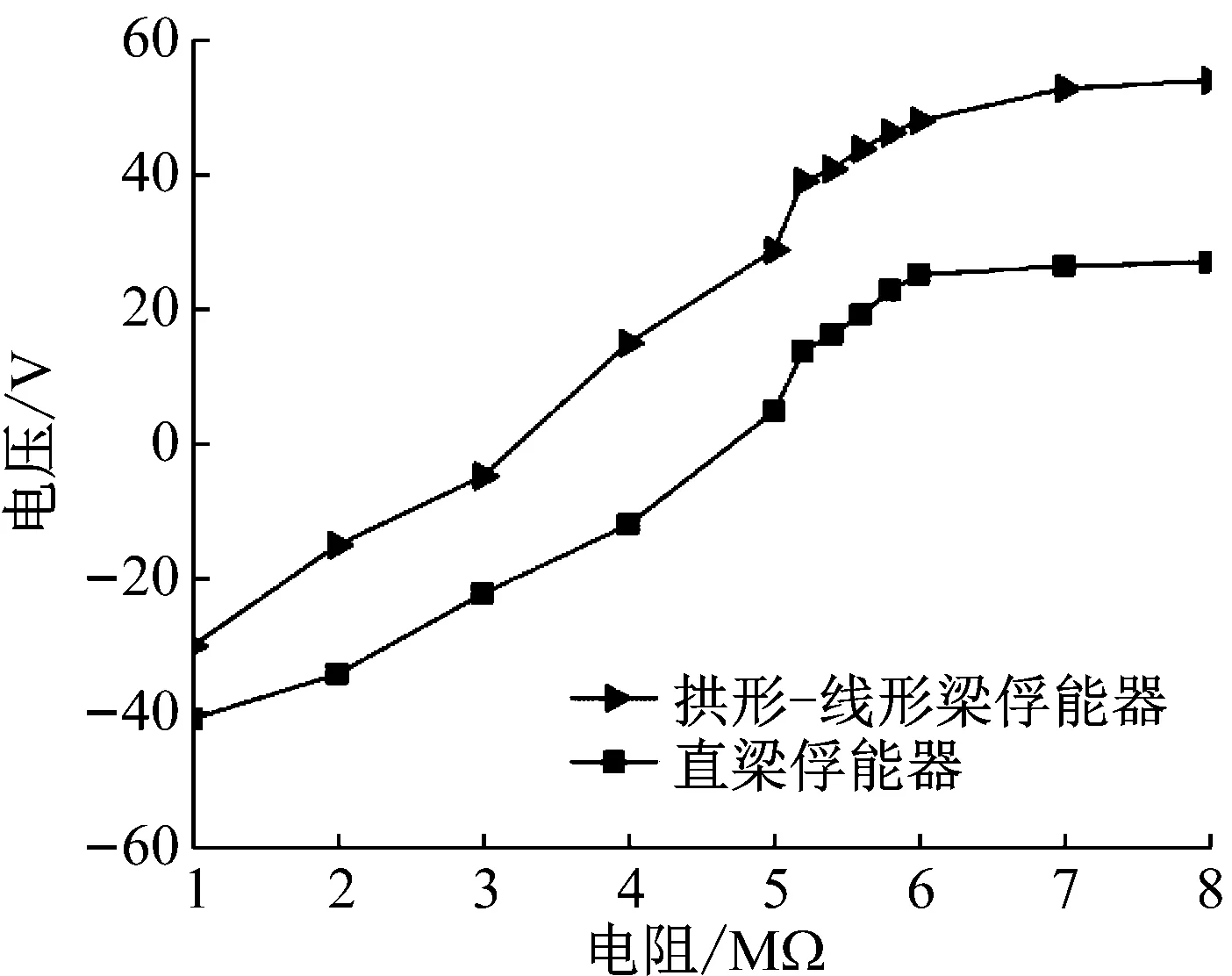
图15 不同阻值条件下拱形-线形梁、直梁俘能器电压输出比较图Fig.15 Comparison of output voltage versus different resistance obtained from the arc-linear harvester and the straight beam harvester

为进一步比较磁力耦合作用下拱形-线形双稳态压电俘能器与传统直梁压电俘能器发电性能，保持激励水平不变，在各自双稳态临界磁距条件下(拱形-线形梁磁距为16 mm，直梁磁距为14 mm)，作扫频(10～20 Hz)电压(开路条件)发电性能实验，对比结果如图16所示。

由于目前暂无评价压电俘能器输出性能统一标准，从图16中可以看出，在同等激励条件下，若取10 V为有效输出电压，拱形-线形压电俘能器与直梁结构俘能器有效工作频带均约为3.2 Hz；但前者峰值电压为34.3 V，而后者峰值输出电压为25.1 V，前者峰值电压约是后者1.3倍；且拱形-线形压电俘能器超出20 V电压带宽为1 Hz，而直梁结构仅为0.3 Hz，实验表明拱形-线形压电俘能器特殊的结构对俘能特性有显著影响，相对于传统直梁双稳态压电俘能器，拱形-线形压电俘能器在不减少大幅响应带宽情况下，可以获得更大的平均输出电压，提升了俘能性能。同时，双稳态拱形-线形压电俘能器大幅响应频率带更靠近低频区域，也更适合于低频环境应用。

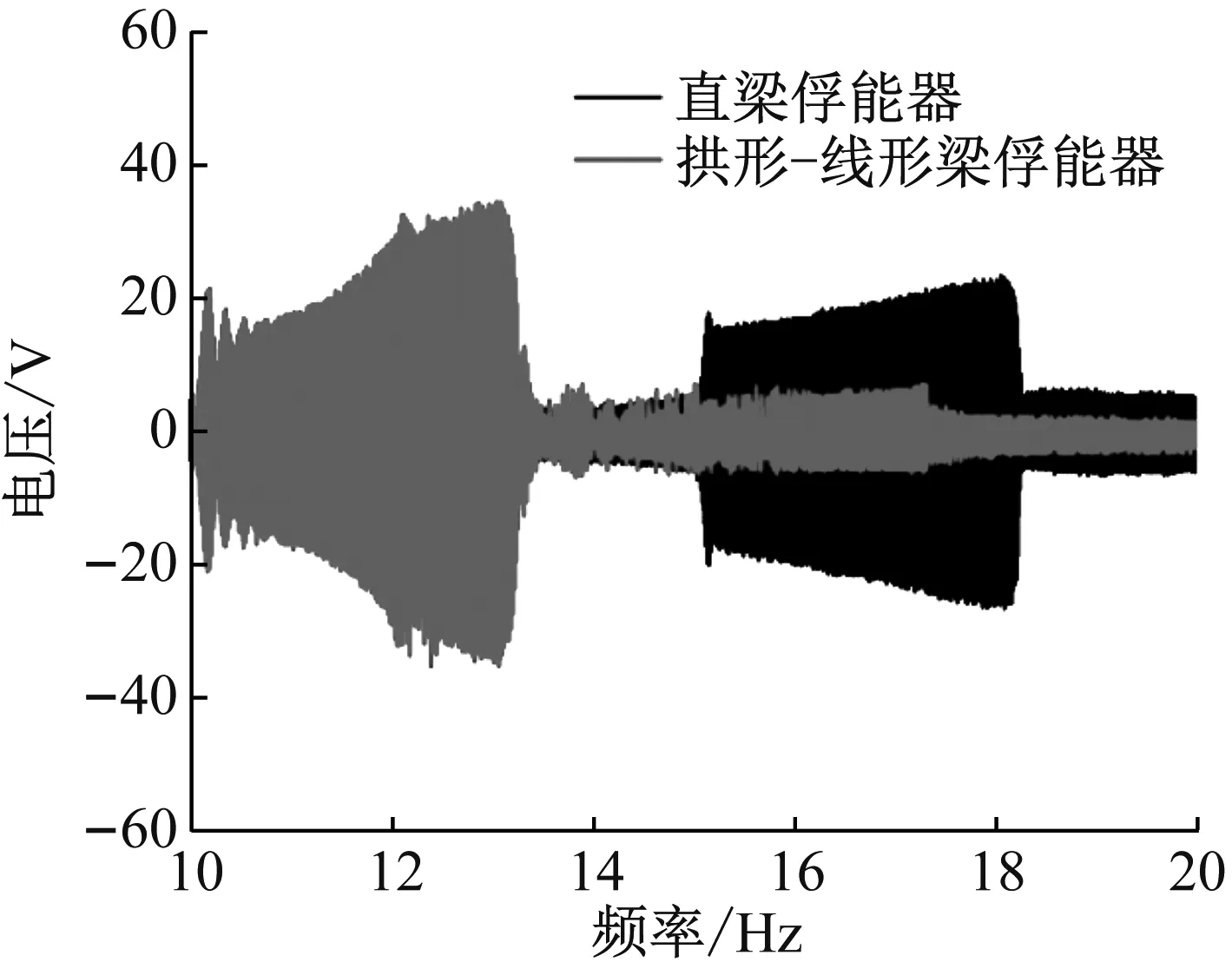
图16 双稳态拱形-线形压电俘能器与双稳态直梁压电俘能器扫频电压输出比较图Fig.16 Comparison of frequency-swept output voltage between the ALEH and the bistable straight harvester

5 结 论

本文设计了基于拱形-线形结构梁磁力耦合双稳态压电俘能器，基于Hamilton变分原理建立了系统的动力学方程，利用谐波平衡法对动力学方程进行求解，分析了不同磁距、不同激励条件等对拱形-线形磁力耦合双稳态压电俘能器俘能特性的影响关系，通过实验验证了理论分析结果的正确性，对比了拱形-线形结构梁与传统直梁式俘能器发电性能，主要有以下结论：

(1) 磁力引入可以构建拱形-线形结构梁双稳态压电俘能器，减小磁距将增加大幅响应带宽，有利于系统在更宽频带俘能，但大幅响应幅值有所减少。同时，小的磁距会产生大的势垒高度，需要足够的激励水平或外部作用力以实现大幅响应，故磁距选择应充分结合激励水平与外部条件。

(2) 拱形-线形磁力耦合双稳态压电俘能器在磁距一定条件下，激励水平对俘能性能的影响规律总体保持一致，即随着激励水平的增加，俘能器大幅位移响应带宽与响应幅值均增大，这将使系统在更宽的频带获得大的电压输出。

(3) 拱形-线形结构梁较传统直梁有更低的谐振频率，应变分布较直梁更大、均匀。同等激励，在不减小大幅响应带宽条件下，拱形-线形磁力耦合双稳态俘能器可获得较直梁结构俘能器更高的平均输出电压；故将拱形-线形梁结构引入非线性压电俘能器有助于提高传统直梁俘能性能。同时，还可将该结构应用于其它多稳态或多方向能量收集装置，以提高传统收集装置性能。