星形四面体型索穹顶构形和预应力分析方法

张爱林,朱莉娜,张艳霞1,,文 闻,林海鹏

(1.北京建筑大学 北京未来城市设计高精尖创新中心，北京 100044；2.北京建筑大学 土木与交通工程学院，北京 100044；3.北京工业大学 北京市高层和大跨度预应力钢结构工程技术研究中心，北京 100124)

索穹顶结构是20世纪末兴起的一种新型大跨度空间结构形式，属于全张力、自平衡体系。该结构由预应力钢索及少量的压杆组成，能充分利用钢材的抗拉强度，结构效率高，随着结构跨度的增加其自重不会明显增加，是一种极具应用前景的大跨度空间结构形式。

索穹顶结构最早源于Fuller[1]提出的张拉整体体系，即在结构中尽可能的减少受压状态而使结构处于连续的张拉状态。在此理论基础上，美国工程师Geiger[2]于1986年提出了Geiger型索穹顶,并在汉城奥运会场馆中采用，这是世界上首次在大跨度结构中采用索穹顶结构。虽然该结构简单，施工难度低，对施工误差不敏感，但由于其上弦索之间无联系，抗侧刚度低，当荷载达到一定程度时容易失稳。因此在1996年Levy[3]对Geiger型索穹顶进行改进，改善了脊索的布置方式，提出了Levy型索穹顶，并运用于亚特兰大奥运会体育馆中。Levy型索穹顶解决了Geiger型索穹顶环向刚度不足的问题，但其网格分布不均，施工复杂。之后我国学者提出了一系列索穹顶结构形式如：肋环人字型[4-5]、鸟巢型[6-7]、凯威特型[8-9]、联方双撑杆型[10]、蜂窝四撑杆型[11]、新型脊杆环撑索穹顶，并对结构进行可静动力性能分析。但这些索穹顶结构形式均没有改善上弦脊索网格分布不均的问题。为了优化索穹顶结构形式，改善上弦脊索网格质量，文章提出了一种星形四面体型索穹顶，并针对该索穹顶结构给出了在理想状态下各索杆初始预应力计算公式，同时给出了在不同矢跨比和不同撑杆高度下各索杆内力计算用表，推导了适合该结构的矢跨比以及撑杆高度，并对该结构的静力性能及自振特性进行了分析，用以说明该索穹顶结构索杆预应力分布规律，验证理论的正确性，以及结构力学性能，为后续研究提供参考。

1 星形四面体型索穹顶结构形态及构造特点

星形四面体型索穹顶三维示意图如图1所示，该结构由单斜索、双斜索、单撑杆、双撑杆、环索、脊索、刚性环梁和上内环索组成。与传统肋环型和葵花型索穹顶相比，其将竖直的撑杆变为斜向撑杆，且在同一空间高度上双撑杆与单撑杆交错布置，单斜索与双斜索交错布置，脊索在环向上连续布置。其中斜索、脊索和撑杆组成一个四面体，并且在四面体中由脊索形成的三角形在水平面上的投影长度相等，然后由六个四面体组成星形单体(如图2(b))且该单体在平面图上(如图2(a))的投影面积相同。星形四面体型索穹顶是由数个星形单体组成，且由内圈向外圈以6的倍数增加，从而保证了结构网格的均匀性，使结构整体性更好。相较于传统的索穹顶结构而言，该结构不仅避免了Gerger型索穹顶在环向上无联系，导致结构环向刚度不足的情况，同时也避免了Levy型索穹顶由于结构构件数量多，施工工作量增大和节点设计难度增加的问题。

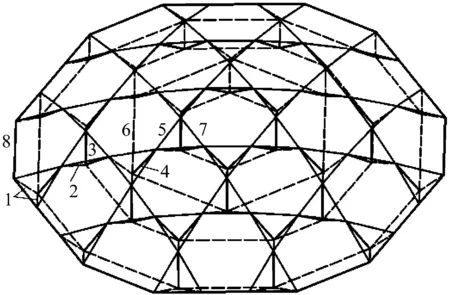
1.双斜索；2.单斜索；3.双撑杆；4.单撑杆；5.脊索；6.环索；7.上内环索；8.刚性环梁图1 星形四面体型索穹顶结构三维图Fig.1 3D model of star-tetrahedron typed cable dome

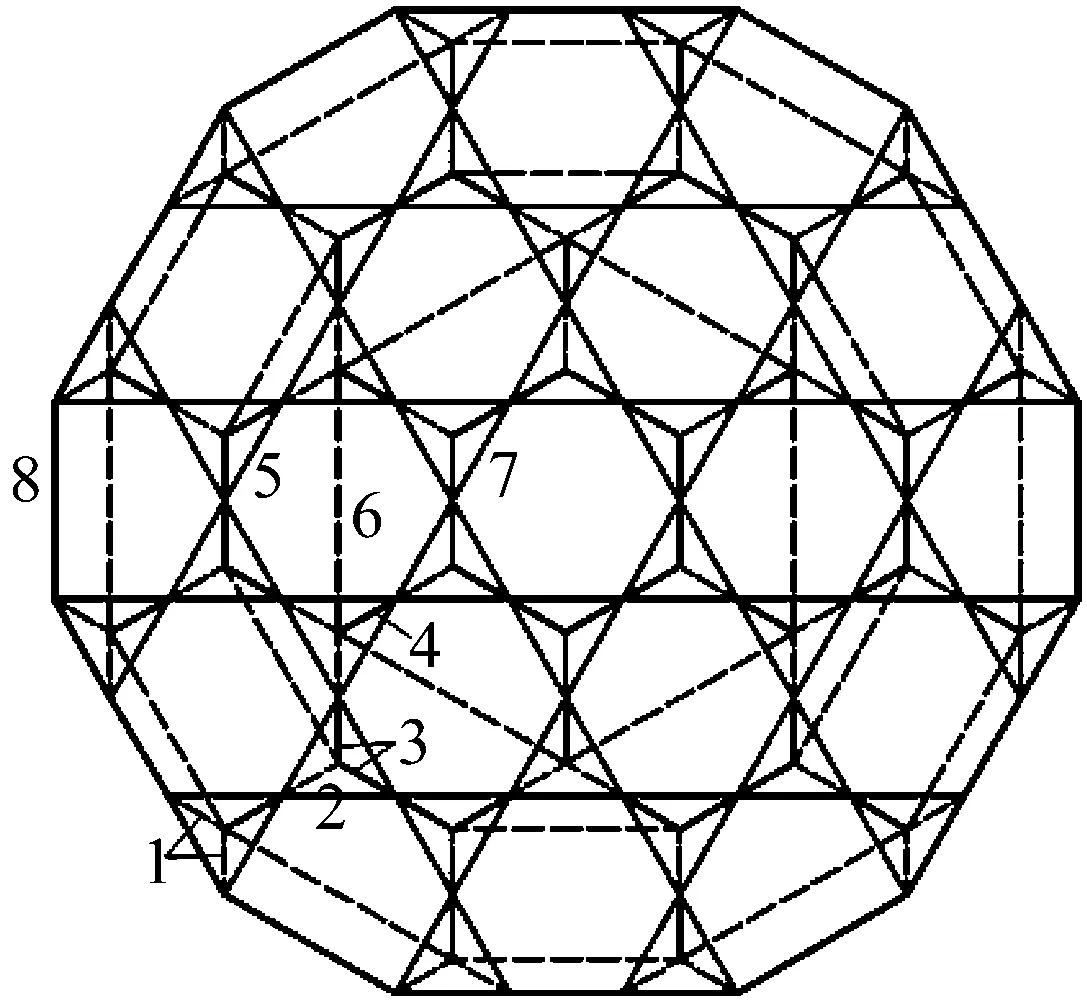
(a) 平面示意

2 星形四面体型索穹顶预应力的简捷分析

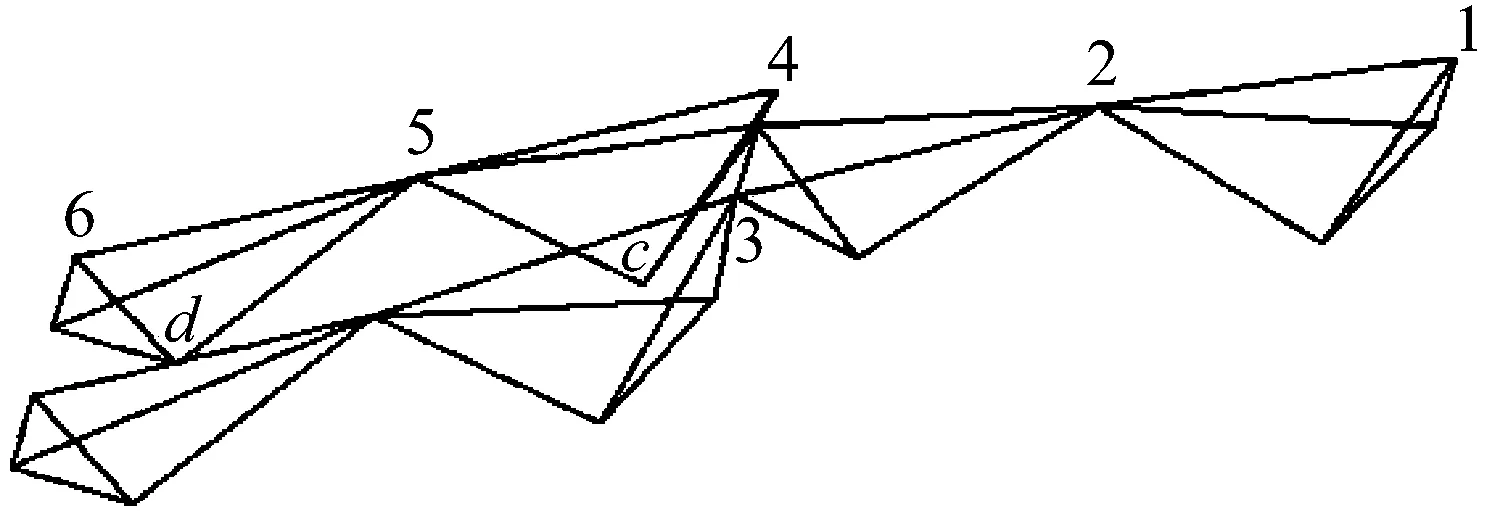
星形四面体型索穹顶结构为沿角对称结构，中心孔为正六边形，对称面上有着相同的索杆布置，预应力以及外荷载，因此仅需研究其1/6结构的半榀即可,其示意图如图3(a)所示。索穹顶外围设置有足够大刚度的刚性环梁，其与索穹顶的连接可以按不动铰支座考虑，所以该结构为一次超静定结构，计算简图如图3(b)所示。

(a) 示意图

(a) 平面图

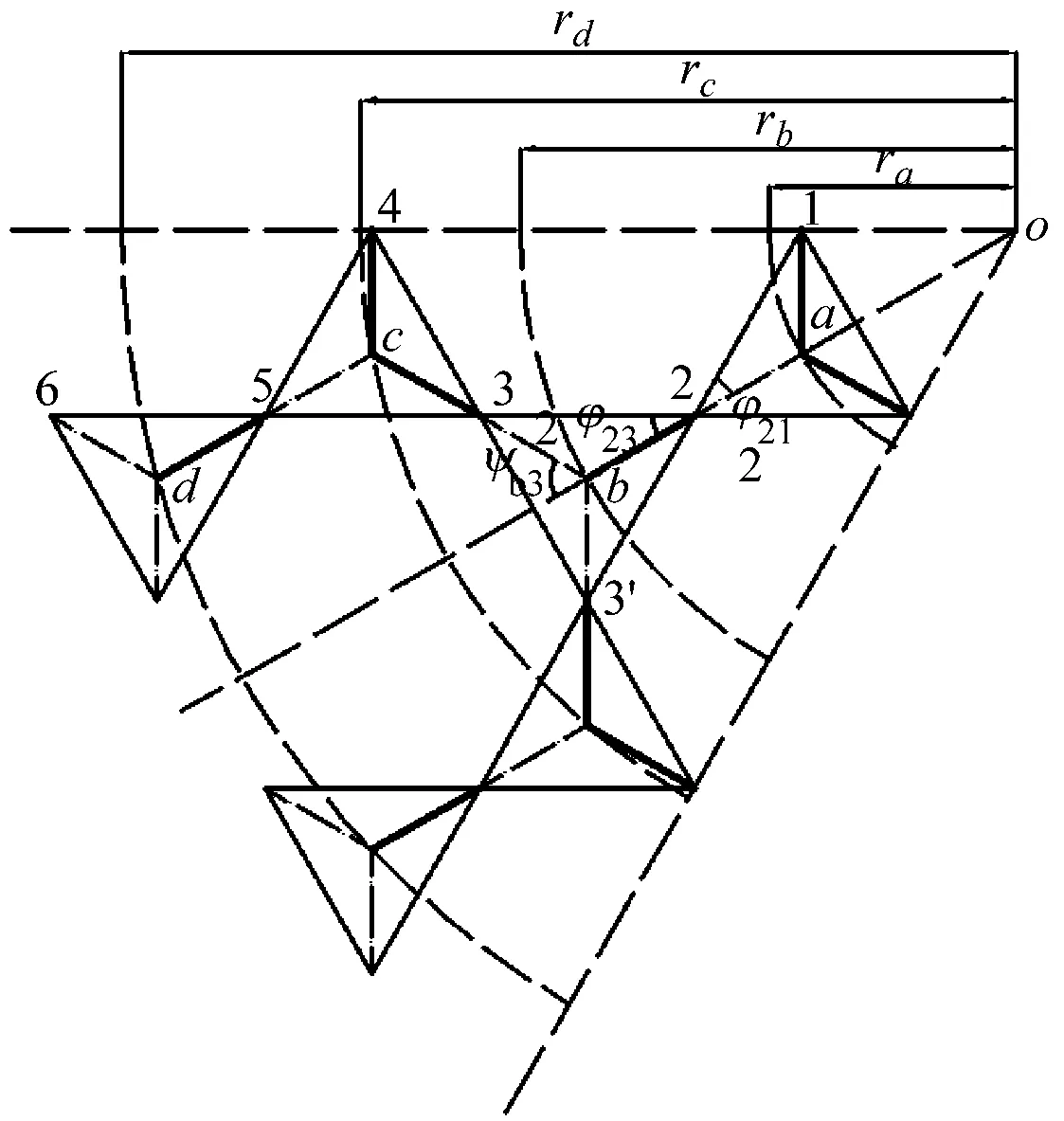
索穹顶初始预应力分析计算时所需平面图与剖面图如图4所示，a、b、c、d为环索、撑杆和斜索的交点,将其统一用m表示，rx为平面投影中交点到六边形中心o的距离；H1为上内环索，Vmi、Ti+1、Bi+1、Hm分别为撑杆、脊索、斜索和环索内力，i代表不同的节点；αi代表斜索与水平面的夹角，其中α53与α54分别为节点53与节点54形成的脊索与水平面的夹角；βi为斜索与水平面的夹角，ξm为经过交点的撑杆与水平面形成的夹角，ξc3与ξc4为由节点c3与节点c5形成的撑杆与水平面的夹角；φi,i+1为由节点i与节点i+1形成的撑杆与对称轴线的夹角；hαi为节点i与节点i+1在剖面图上的垂直长度，hβi为节点i与其相连交点的垂直长度与hαi的差值。

根据图4所示的几何关系，可求得各索杆与水平面夹角，以及与对称轴线之间的夹角等。以索穹顶内环双撑杆的实际内力Va1为基准，利用节点平衡法推导1、2、a和b节点对应的各索杆的内力，如式(1)～(4)所示：

节点1：

(1)

节点a：

(2)

节点b:

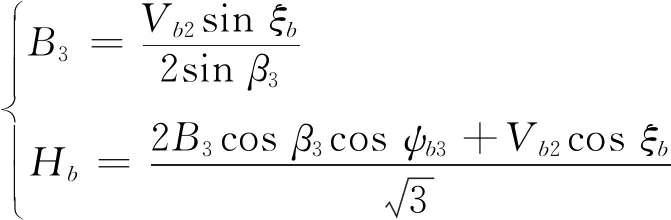
(3)

节点2:

(4)

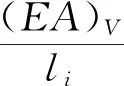
(5)

F3x,F3y，F3z分别为节点3上的已知外力在x，y，z方向上的分量，其计算式如式(6)

F3x=T3cosα3+B3cosβ3cos(ψb3-π/6)

F3y=B3cosβ3sin(π/6+ψb3)

F3z=T3sinα3+B3sinβ3

(6)

由于结构在成形后刚度足够大，节点3在外力作用下产生的节点位移较小，可忽略当x(y,z)方向产生位移时对y(x,z)或者z(x,y)方向的影响，即kx(y,z)=ky(x,z)=kz(x,y)=0。然后由式(5)、(6)即可求出节点3在两个方向上的位移，如式(7)所示，其中为斜索与对称轴线之间的夹角。将节点3的位移转换到各索杆轴线上，然后根据各索杆刚度即可求出各索杆内力，见式(8)，式中ω为节点3与4在水平面夹角。

因节点5在平面竖直方向没有分量，也即F5y=0，Δ5y=0,因此只需求两个方向的位移即可。同节点3可求得节点5在x，z两个方向的位移，以及节点5上各索杆内力见式(9)、(10)

(7)

节点3：

(8)

节点5：

(9)

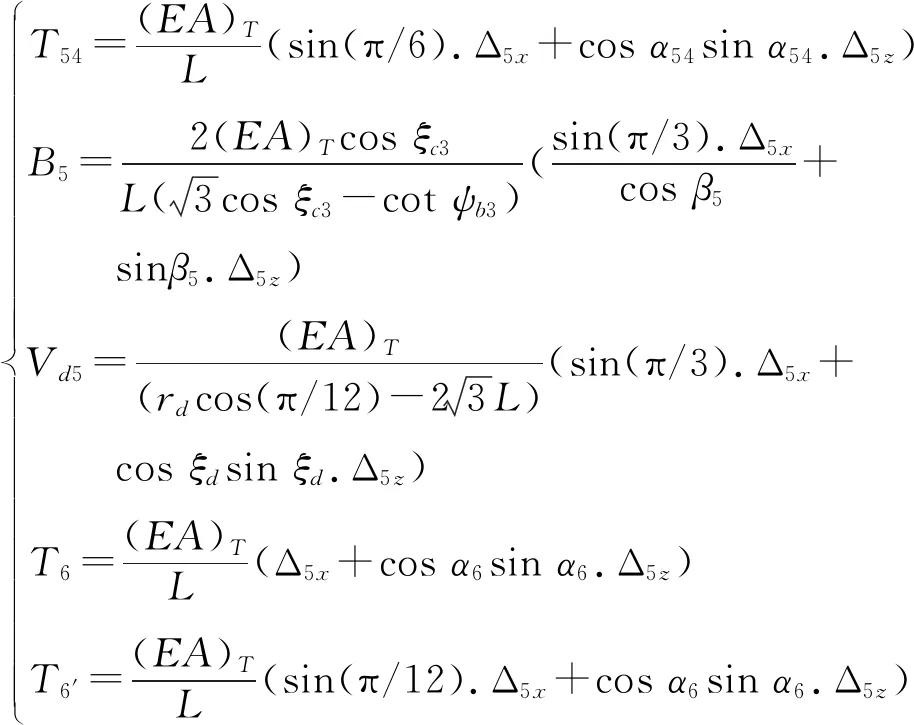
(10)

节点c，由于Vc3和B5内力已知，仅有两个未知力，则可利用节点平衡法求解，如式(11)

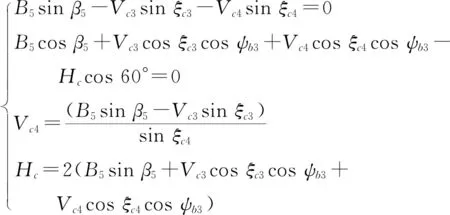
(11)

节点d:

(12)

3 预应力态索杆内力参数分析

设星形四面体型索穹顶跨度L0=78 m，内孔半径L1=Δ，矢高为f，穹顶半径为R，索穹顶结构半榀平面桁架简化图如图5 所示。各径向脊索在对称平面的投影再投影到水平面的长度均为Δ，撑杆下节点在水平面的投影分别在脊索水平面投影的1/3和2/3处并交替布置，各环索在水平面投影的间距相等均为Δ，为简化计算令hα=hβ。由几何关系可求得R,ra,αi,βi等，具体计算如下式(13)，式中L为脊索在水平投影上三角形边长。将式(13)代入式(1)～(12)可得到各索杆内力，当f/L0取值为1/12.5、1/10、1/8.5、1/6，Va1取值为-20.00，求得各索杆内力的计算结果如表1所示。

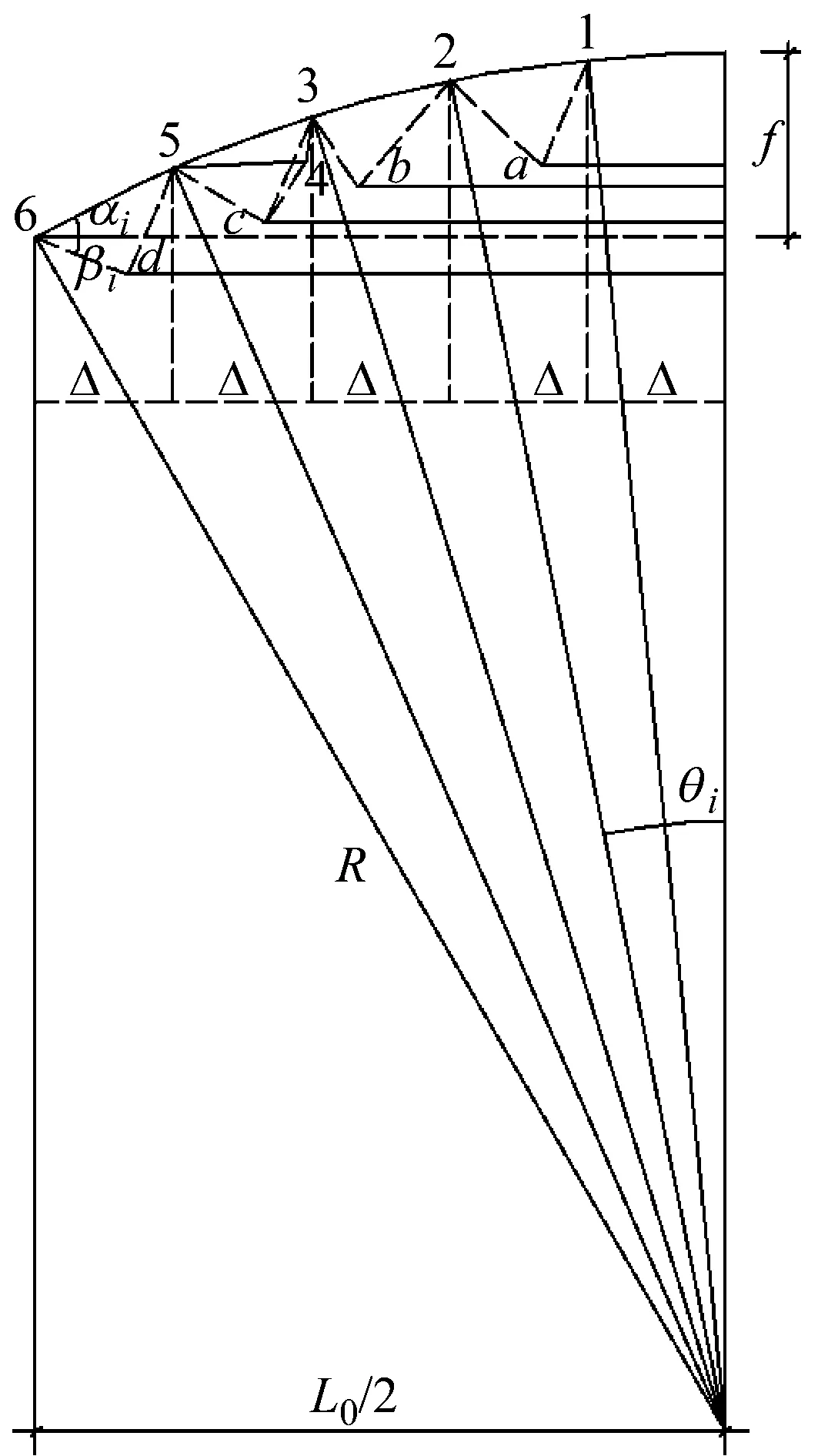
图5 结构简化半榀平面桁架图Fig.5 Simplified semi-structure of plane truss

固定结构矢跨比，研究撑杆高度对索穹顶结构内力分布的影响。保持脊索在对称平面的投影再投影到水平面的长度为Δ，矢跨比为1/10和1/8.5，其他几何参数与不同矢跨比下的参数保持一致。对于矢高且形状确定的索穹顶结构，hα已由式(13)求出，则撑杆的高度由hβ控制。分别取hβ=Δtan 10°、hβ=Δtan 15°、hβ=Δtan 20°、hβ=Δtan 25°和hβ=Δtan 30°，Va1=-25.00，由式(1)～(13)可得各索杆预应力分布情况，其计算结果如表2所示。

(13)

由表1可看出，对于星形四面体型索穹顶结构，随着结构矢跨比的增加，各索杆内力逐渐减小，内圈索杆内力变化相对较小，外圈索杆内力变化较大。同时从表中可以看出矢跨比在1/12.5时，各索杆内力最大，环索内力最大值达到4 223 kN，相对于1/10跨度时，差值达到35%，此时环索内力过大不利于现场张拉，不建议采用此矢跨比。而当结构矢跨比为1/6时，结构起拱大，而索杆内力又相对较小，在外荷载作用下索容易发生松弛，所以也不建议采用。因此对于该结构而言，建议矢跨比取值在1/10～1/8.5，此时索杆内力分布均匀，索力大小合适，利于实际张拉，。

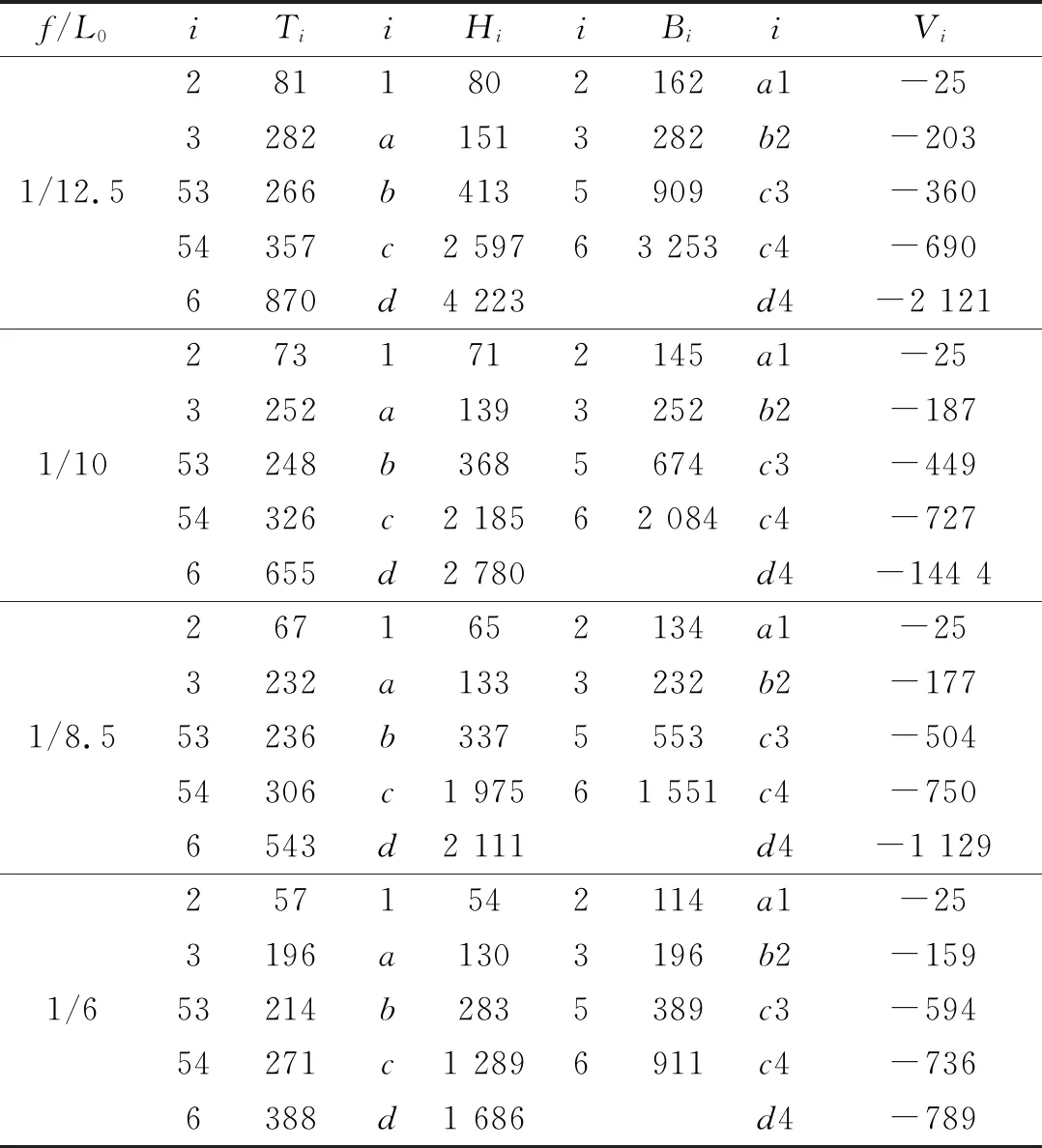
表1 不同矢跨比时星形四面体型索穹顶索杆内力Tab.1 Prestressing force distribution and struts’internal forces of star-tetrahedron type cable dome with different rise-span ratios

表2与表3分别为矢跨比为1/10和1/8.5时，不同撑杆高度所对应的结构索杆内力，从表中可发现，在这两种矢跨比下结构索杆内力变化趋势相近，当撑杆高度变化Δtan 5°时，索杆内力变化最高可达64%，说明改变撑杆高度比改变矢跨比对结构内力影响更大。同时可看出，当矢跨比分别为1/10和1/8.5，撑杆高度hβ=Δtan 10°时，索力最大值分别达到5 931 kN和6 130 kN，索力值过大，不利于实际施工张拉。而当撑杆高度hβ=Δtan 30°时，此时结构实际撑杆高度为10.68 m，且结构索杆内力小，因此在外荷载作用下，索容易发生松弛。当撑杆高度在Δtan 15°、Δtan 20°和Δtan 25°时，索内力和撑杆内力均均匀变化，且索内力最大值仅为2 168 kN，便于结构张拉。

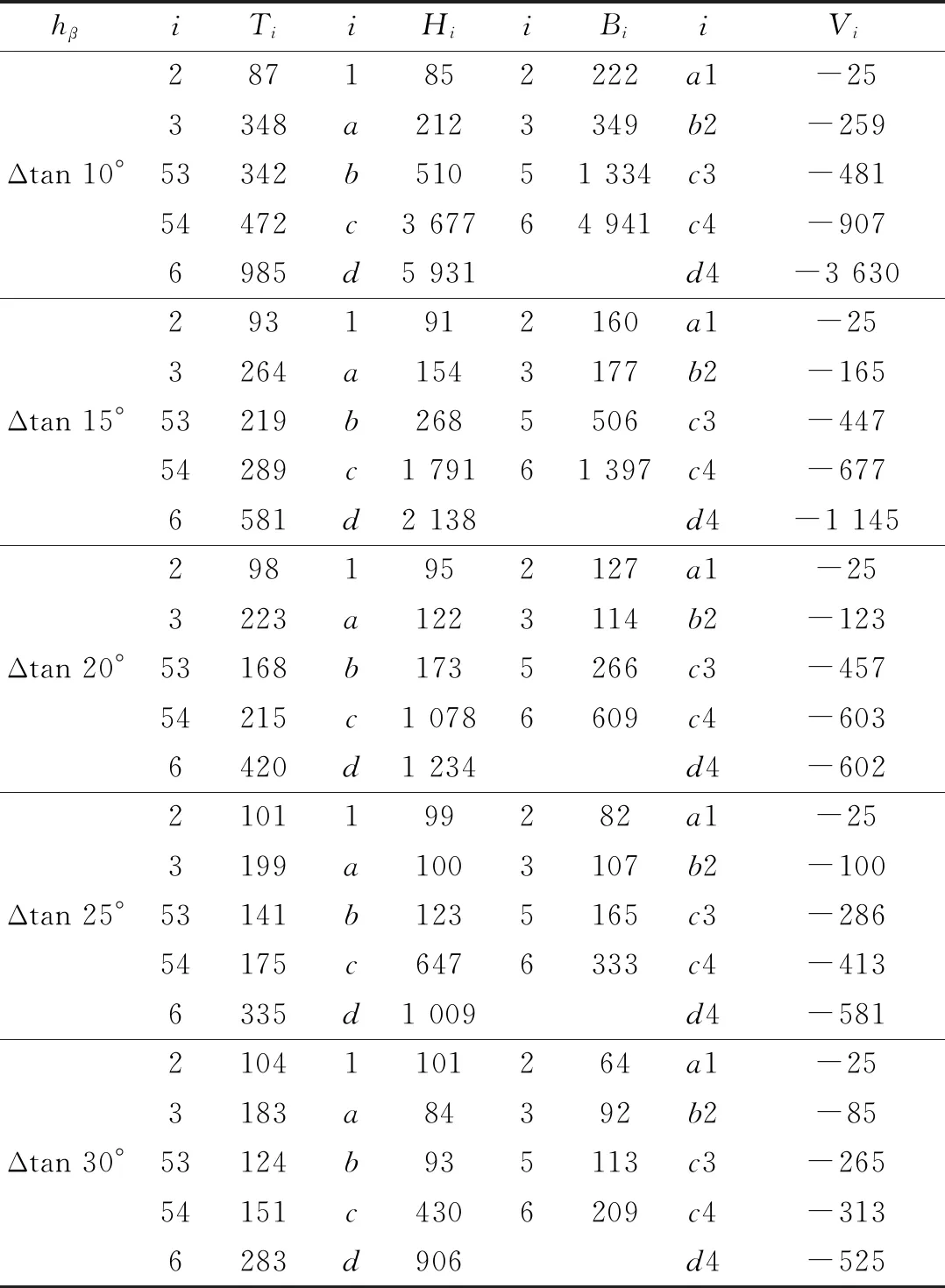
表2 1/10矢跨比时不同撑杆高度对星形四面体型索穹顶索杆内力Tab.2 The internal force of each cable rod of star tetrahedron cable dome with different strut height under 1 / 10 rise span ratio

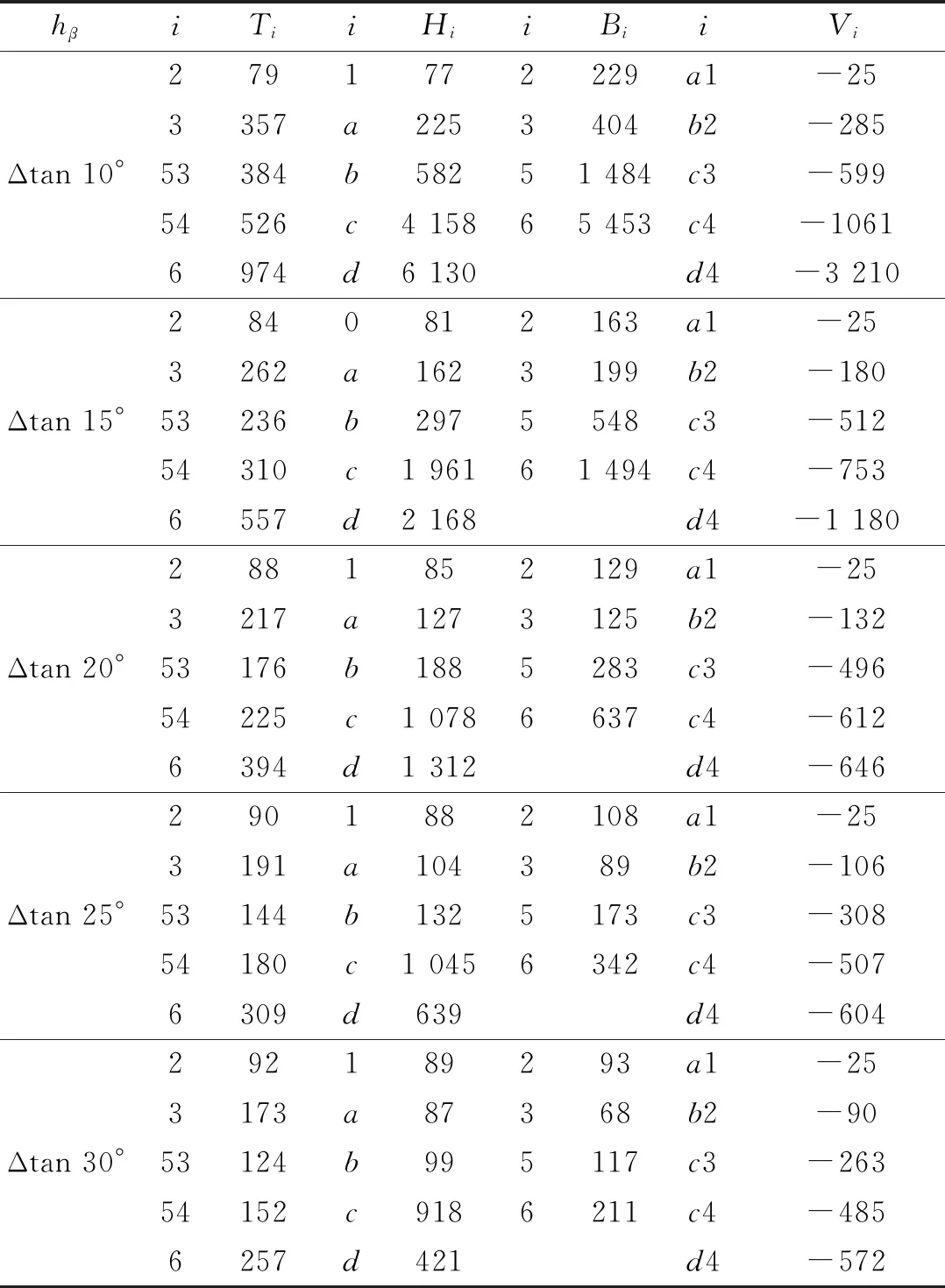
表3 1/8.5矢跨比时不同撑杆高度对星形四面体型索穹顶索杆内力Tab.3 The internal force of each cable rod of star tetrahedron cable dome with different strut height under 1 / 8.5 rise span ratio

综上所述可得，对于该星形四面体型索穹顶结构，矢跨比宜为1/10～1/8.5，对应的撑杆高度宜在Δtan 15°～Δtan 25°。

4 星形四面体型索穹顶结构关键性能分析

4.1 静力性能分析

根据前面理论分析，利用MIDAS软件对结构进行全跨均布荷载作用下的静力性能分析，结构跨度取为78 m，矢跨比为1/10，撑杆高度hβ=Δtan 25°，研究结构在1.3倍恒荷载与1.5倍活荷载(活荷载大小为0.5 kN/mm2，恒荷载仅为膜的重量，其值为0.1 kN/mm2)作用下结构索杆内力变化与无外荷载时的预应力态进行对比，忽略膜材对结构刚度的影响。外荷载先以均布荷载的方式施加到结构上，然后转换为等效集中质量作用在结构的上弦节点，荷载布置位置以及构件编号如图6所示。

从表4可看出，在全跨均布荷载作用下撑杆内力和环索内力与无外荷载的预应力态相比较均有所增加，斜索内力与脊索内力逐渐减小，内圈索杆内力值变化较大，外圈内力变化相对较小。在外荷载作用下，相较于其他杆件，结构脊索相对容易松弛，最内圈脊索T1预应力值为71 kN，相对于无外荷载的预应力态，脊索初始内力损失达到66.1%，但依旧处于张拉状态，未发生脊索松弛的现象，说明结构具有较强的初始刚度与承载能力。

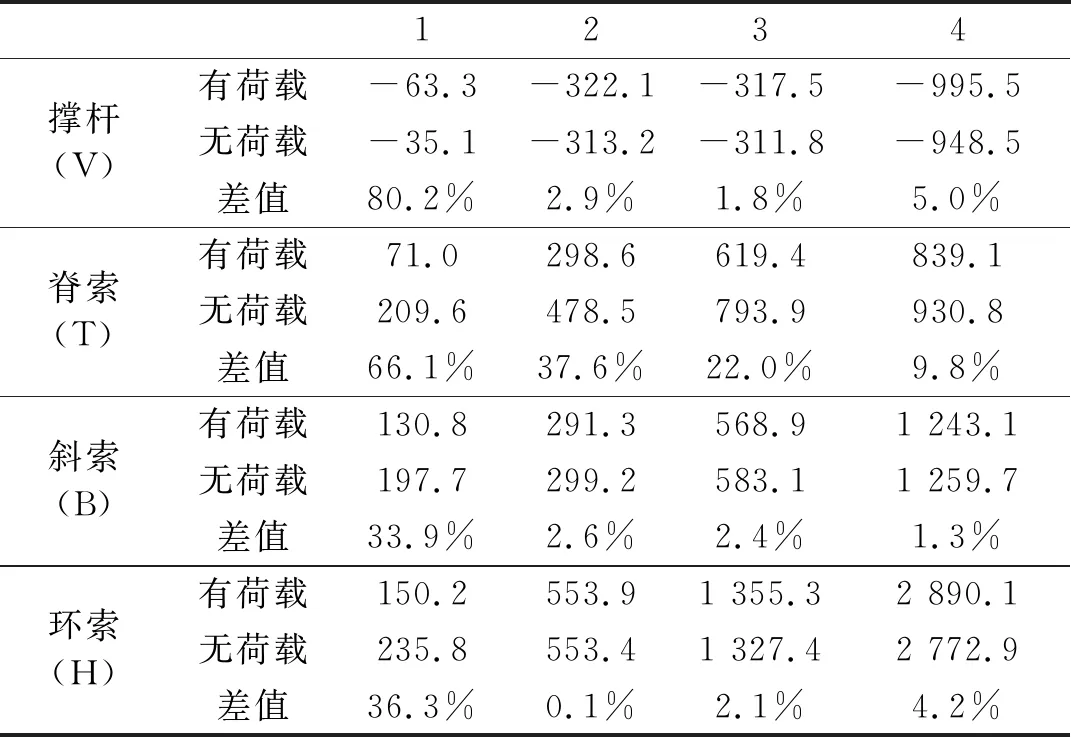
表4 结构有荷载态与无荷载态索杆内力对比Tab.4 Comparison of internal forces of cable strut in loaded and unloaded state

4.2 自振特性分析

采用与静力分析相同的计算模型，在计算中将1倍恒荷载与1倍活荷载(共计0.6 kN/mm2)施加在结构上，同样将均布荷载转换成等效节点荷载施加在结构上弦节点，提取结构前50阶自振频率和模态振型进行分析。

结构前50阶自振频率如图7所示，从图中可看出结构前15阶自振频率相对集中，结构第2、3、11、12以及13阶自振频率均相差不大，这是因为索穹顶结构具有对称性，但由于建模时存在微小误差，导致结构自振频率存在微小误差。结构不存在明显的跳跃点，说明结构刚度分布均匀，不存在明显的薄弱部位。表5为结构前5阶振型及对应的自振频率，结构第1阶Z向振型方向因子占比最多，结构第2阶X、Y向振型方向因子占比较多，第3～5阶分别为Y向变形、环向变形以及X向变形，且变形均由内圈开始。从前5阶的变形状态来看，结构竖向刚度弱与结构环向刚度，结构环向刚度较好，且结构内圈刚度弱与结构外圈刚度，这是因为内圈脊索、斜索以及撑杆数量相对较小，对结构内圈约束不足，内圈刚度小。

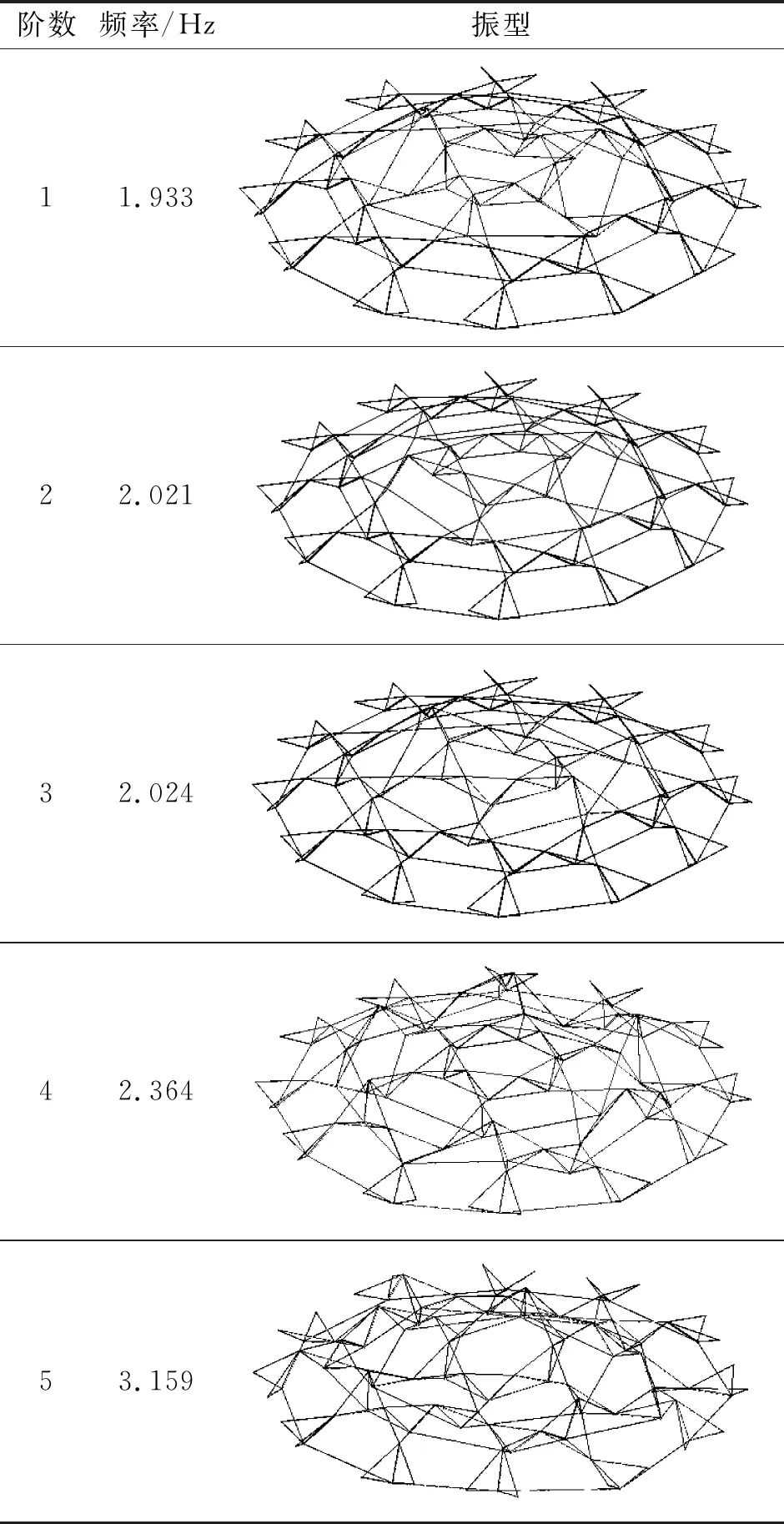
表5 结构前5阶振型及频率Tab.5 First 5 modes and frequencies of structure

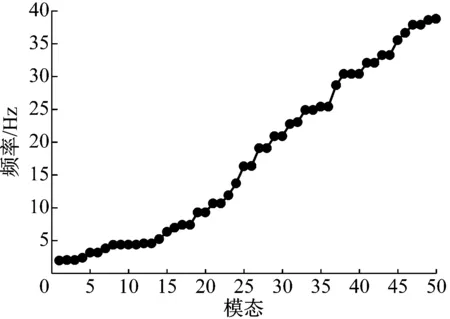
图7 结构前50阶自振频率Fig.7 First 50 natural frequencies of structure

5 结 论

本文提出了一种新型索穹顶结构形式即星形四面体型索穹顶，相对于传统的索穹顶结构而言，由于在环向上通过脊索联系，增加了结构抗侧刚度和对抗非对称荷载能力，同时上弦脊索网格布置均匀，结构整体稳定性增加。

另外提出利用节点平衡法和位移法推导结构在成形状态下的初始预应力计算公式，并给出算例，得到在不同矢跨比和不同撑杆高度下各索杆内力计算表，并给出了该结构的合适矢跨比以及撑杆高度，为后续进一步研究和力学性能分析提供依据。在此基础上分析了结构在全跨均布竖向荷载作用下的静力性能以及自振特性分析。其结果表明：

(1) 随着矢跨比和撑杆高度的增加，各索杆初始预应力由内圈到外圈均呈减小趋势，且相较于改变结构矢跨比，改变撑杆高度对各索杆预应力分布影响明显。

(2) 对于该结构而言，矢跨比宜为1/10～1/8.5，所对应的撑杆高度宜在Δtan 15°～Δtan 25°，此时结构索杆内力变化均匀，方便实际张拉施工。

(3) 结构在全跨均布竖向荷载作用下，脊索、环索与斜索均未出现索松弛的现象，说明结构具有较强的承载能力，具有优越的力学性能。

(4) 结构自振频率分布密集，无明显跳跃点，结构竖向刚度弱与环向刚度，结构环向刚度大。