铁路重力式桥墩抗震计算简化模型研究

鲁锦华，陈兴冲，丁明波，马华军，张熙胤

(兰州交通大学 土木工程学院，兰州 730070)

铁路重力式桥墩因配筋率较低其破坏特征不同于普通钢筋混凝土桥墩。鞠彦忠等[1-2]对配筋率为0.1%和0.2%的铁路重力式桥墩进行的拟静力试验研究中发现桥墩破坏时混凝土压碎不明显，且仅在墩底产生一条或多条裂缝。蒋丽忠等[3]对高速铁路重力式桥墩的研究中也发现桥墩破坏时墩底未形成明显的塑性铰区。Chen等[4-5]对铁路重力式矩形截面桥墩的研究中发现配筋率为0.1%的桥墩破坏时仅在墩底产生一条裂缝。以上研究发现铁路重力式桥墩破坏时墩底未形成明显的塑性铰区，且破坏部位主要集中在墩底，明显区别于钢筋混凝土桥墩的延性破坏特征。作者在前期研究中对配筋率为0.2%的铁路重力式桥墩进行了拟静力试验和振动台试验发现仅在墩底形成一条主裂缝，且在动力作用下有明显的摇摆现象[6]。

针对破坏部位主要集中在墩底，且未形成塑性铰区的铁路重力式桥墩，目前主要采用实体单元模型或者纤维单元模型进行分析。刘浩[7]采用ANSYS软件建立了铁路重力式桥墩的抗震分析模型，并对其抗震性能进行了分析。邵光强等[8-9]采用纤维单元模型对高速铁路重力式桥墩进行了分析。研究发现实体单元和纤维单元可以有效模拟铁路重力式桥墩的抗震性能，但是建模过程繁琐，计算效率较低，时间成本较高。

依据低配筋铁路重力式桥墩在墩底仅形成一条主裂缝，且在动力作用下有明显的摇摆现象，发现该类桥墩具有墩底自由摇摆桥墩的特征。而目前国内外对于摇摆桥墩的抗震分析模型研究较为成熟[10-14]。夏修身[15]对于自由摇摆桥墩提出了简化的双弹簧模型；贾登峰[16]提出了设置限位钢筋的基底隔离桥墩计算分析模型，在自由摇摆模型的基础上，设置只受拉的杆单元模型纤维钢筋；马华军[17]针对设置限位钢筋的基底隔离桥墩的计算分析模型进行了简化，将杆单元简化为只受拉的非线性弹簧。参考现有摇摆桥墩的抗震分析计算模型，本文提出了一种适用于低配筋铁路重力式桥墩的简化的四弹簧模型，用于铁路重力式桥墩的简化抗震分析。

1 简化的抗震分析模型

依据低配筋铁路重力式桥墩在静力作用下的破坏特征及在地震作用下的摇摆特征，参考自由摇摆桥墩的双弹簧模型，考虑纵向钢筋的约束作用，提出适用于铁路重力式桥墩的简化的四弹簧抗震分析模型。

自由摇摆桥墩双弹簧模型中墩身采用弹性梁单元模拟，桥跨质量简化为墩顶集中质量，墩底刚臂单元模拟墩身受力方向截面宽度，只受压的弹簧模拟自由摇摆时桥墩的提离，计算模型如图1所示。受压弹簧的刚度k按式(1)、(2)及(3)近似计算。

图1 自由摇摆桥墩两弹簧模型Fig.1 Two-spring model of free-rocking piers

(1)

(2)

(3)

式中:Kv为竖向刚度；R0为等效半径；A0为墩底扩大基础的截面积；G为墩底材料的剪切模量；ν为墩底材料的泊松比。

在自由摇摆桥墩双弹簧模型的基础上，再考虑墩身纵向钢筋的受拉作用，采用非线性弹簧模拟只考虑受拉不考虑受压的纵向钢筋，受拉弹簧屈服前刚度按式(4)计算。综上分析，得到适用于铁路重力式桥墩的四弹簧计算模型如图2所示。

(4)

式中:kx为钢筋屈服前刚度；E为纵向钢筋的弹性模量；As为参与计算的纵向钢筋的总面积；Ld为纵向钢筋计算长度。

图2中，Fy为纵向钢筋的屈服力；a点对应纵向钢筋屈服点；Δy为屈服位移。纵向钢筋受拉单元的滞回规则为：①→②为加载路径，③为卸载路径；④→⑤为再加载路径。

图2 四弹簧抗震分析模型Fig.2 The four-spring seismic analysis model

文献[17]针对墩底摇摆桥墩采用四弹簧模型分析了限位钢筋对自由摇摆桥墩的影响，而本文主要是针对低配筋铁路重力式桥墩进行的抗震简化分析，二者研究对象不同，且参数取值也不同。文献[17]中限位钢筋仅配置单根钢筋，且计算受拉弹簧的刚度时，钢筋取实际钢筋长度。本文提出的四弹簧模型，钢筋配置在墩身四周，计算受拉弹簧钢筋时，钢筋面积取值为受拉区纵向钢筋面积之和，且钢筋计算长度依据文献[6]中模型桥墩试验数据进行确定，配筋率为0.2%的桥墩应变测点及钢筋应变如图3所示。研究发现随着位置的增加，钢筋的应变逐渐减小，距离墩底10 cm时，高度约为等效塑性铰长度(15.9 cm)的2/3倍，最大应变为钢筋为514 με，为屈服应变的1/3左右；距离墩底20 cm时，高度约为等效塑性铰长度的5/4倍，钢筋应变仅为139 με，远远小于钢筋的屈服应变，该处的钢筋几乎不受力，计算时该处以上的钢筋长度可以不予考虑。结合试验数据，最终四弹簧抗震分析模型中钢筋计算高度Ld可按等效塑性铰长度取值，且物理意义明确，同时下文的计算结果与试验值的比较也证明了钢筋计算高度Ld按等效塑性铰长度取值的可行性。

2 模型验证

为了验证简化的四弹簧模型，采用文献[6]中的试验模型桥墩进行对比，墩高为125 cm，截面尺寸为36×25 cm，剪跨比为5.0，轴压比为4%，各模型桥墩的设计参数如表1所示。

表1 模型桥墩设计参数Tab.1 Design parameters of model piers

采用四弹簧抗震分析模型对桥墩进行计算分析，得到模型桥墩的滞回曲线与骨架曲线，并与试验值进行比较，如图4和图5所示。

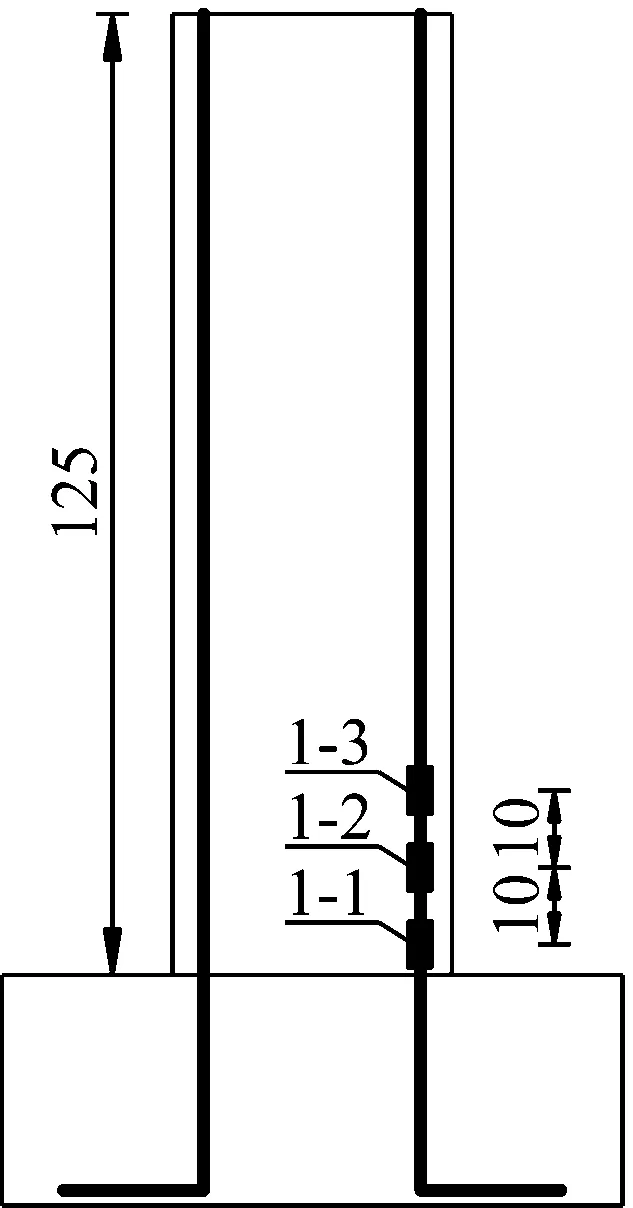
(a) 墩身应变测点

(a) S1桥墩

计算得到的滞回曲线与试验结果对比发现，配筋率为0.2%的桥墩滞回曲线计算值与试验结果吻合较好；随着配筋率的增加，计算得到的滞回曲线相比于试验结果的“捏缩”效应更为明显。计算得到桥墩的骨架曲线与试验结果吻合较好，通过极限承载力的对比发现(如表2所示)，配筋率较小时，计算值比试验值偏高，而配筋率较大的桥墩，试验值比计算值偏高，但最大误差在8%以内。说明简化的四弹簧模型可以预测低配筋的铁路重力式桥墩在静力作用下的水平承载力，能有效的模拟桥墩的受力特性，验证了简化四弹簧模型计算低配筋铁路重力式桥墩抗震性能的准确性和合理性。

表2 极限承载力对比Tab.2 Comparisons of ultimate loads

分析得到桥墩试验值和计算值的刚度退化曲线，如图6所示。

(a) S1桥墩

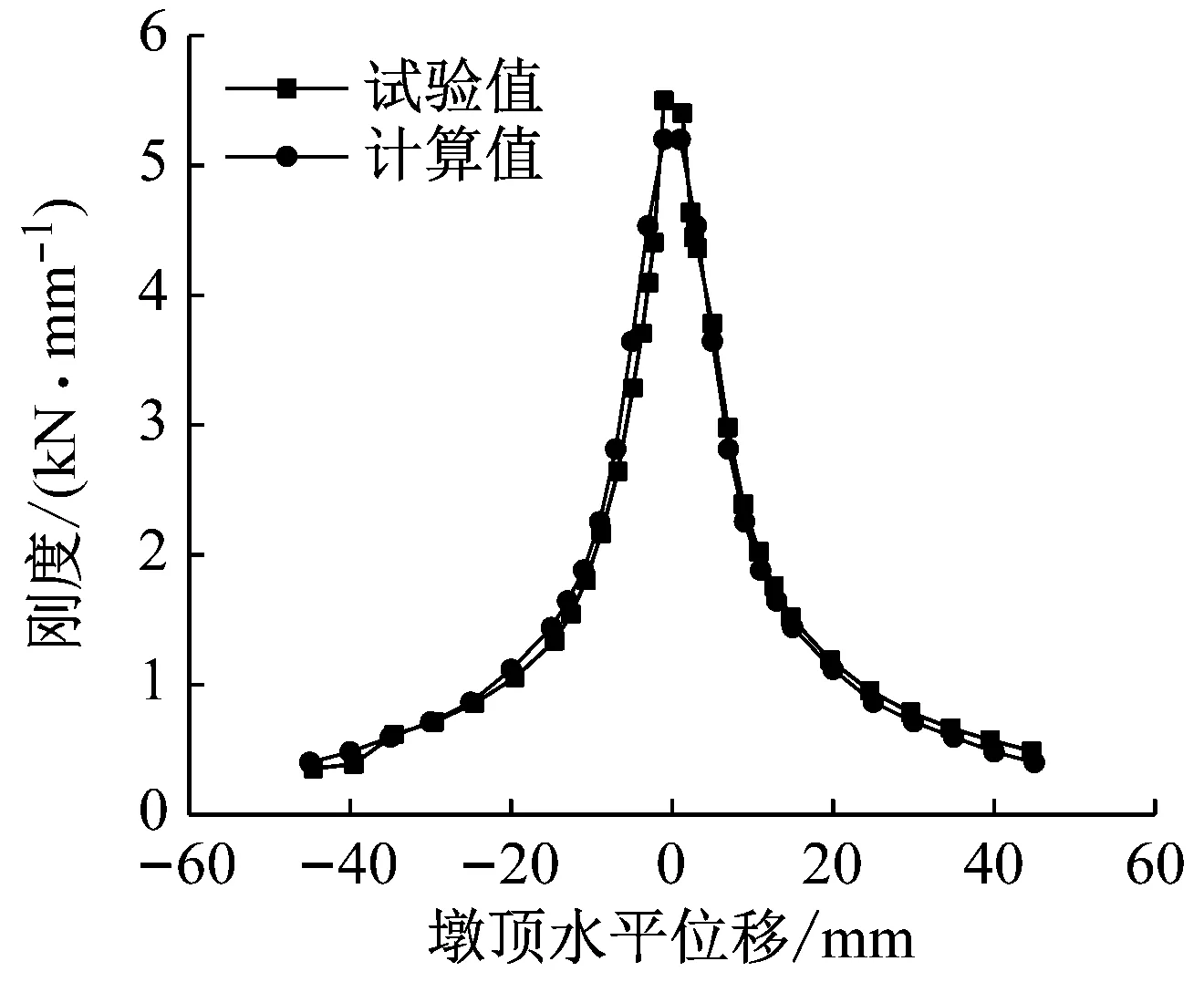
(a) S1桥墩

由图6可以看出，计算得到桥墩的刚度退化曲线与试验结果基本吻合。加载初期，桥墩刚度的试验值比计算值偏高；当桥墩开裂后，且墩顶加载位移较小时，桥墩刚度的计算值比试验值偏大；加载后期，计算值与试验值基本吻合。桥墩刚度退化计算值与试验值的变化趋势基本一致，说明简化模型可有效模拟桥墩的刚度退化特性。

由图7可以看出，配筋率为0.2%的桥墩，计算得到的累计耗能与试验结果吻合较好；随着配筋率的增大，计算结果与试验结果误差逐渐增大，其主要原因可能是试验中正反加载方向无法完全对称，骨架曲线(图5)中可以明显的看到，墩顶加载位移小于20 mm时，正向加载的承载力的计算值比试验值偏大，最终导致计算结果的滞回环所包含的面积比试验结果偏大。

(a) S1桥墩

采用四弹簧抗震分析模型对桥墩进行了动力响应分析，得到模型桥墩的墩顶相对位移和墩顶绝对加速度的响应，并与试验值进行比较如图8所示。在进行每个工况的试验前对模型桥墩输入白噪声，测得结构的频率，7度设计地震和8度罕遇地震前模型桥墩的频率分别为8.9 Hz和8.3 Hz，四弹簧模型计算的频率均为8.5 Hz。

(a) 7度设计地震作用下墩顶相对位移

由图8中可以看出，7度设计地震作用下墩顶相对位移及绝对加速度的四弹簧模型计算值与试验值吻合较好；8度罕遇地震下墩顶相对位移四弹簧模型计算为9.13 mm，试验值为10 mm，误差仅为4.7%，墩顶绝对加速度四弹簧模型计算值为0.366g，试验值为0.35g，误差为4.6%。说明简化的四弹簧模型可有效模拟桥墩的墩顶相对位移及墩顶绝对加速度，同时验证了四弹簧模型计算桥墩动力响应的准确性和合理性。

3 结 论

通过铁路重力式桥墩试验及数值分析模型研究得到如下结论：

(1) 基于配筋率较低的铁路重力式桥墩的破坏现象，在自由摇摆桥墩双弹簧模型的基础上，增加考虑钢筋约束的非线性受拉弹簧，提出了适用于低配筋铁路重力式桥墩的四弹簧模型抗震分析模型。

(2) 依据试验模型结果，确定了只受拉弹簧刚度计算参数取值。钢筋面积取受拉区纵向钢筋面积之和，钢筋计算高度可取等效塑性铰长度。

(3) 静力作用下和动力作用下，四弹簧模型计算值与试验值均吻合加好，验证了四弹簧抗震分析模型可用于铁路重力式桥墩的抗震性能分析及动力响应分析。