近区爆炸作用下砌体填充墙损伤破坏与动态响应的数值模拟
2021-05-17胡嘉辉
胡嘉辉,吴 昊,方 秦
(1.同济大学 土木工程学院,上海 200092;2.陆军工程大学 爆炸冲击防灾减灾国家重点实验室,南京 210007)
砌体墙性能优异、成本低廉且易于获取,在世界范围内有着广泛应用。Ettouney等[1]估计全球70%以上的现存建筑为砌体结构,除此以外,绝大多数建筑的围护结构仍以砌体填充墙为主。美国ABS防爆顾问咨询公司[2]的研究发现,恐怖袭击中高达75%的民众伤亡来自于爆炸中门窗、玻璃及墙体等产生的飞散碎片形成的二次伤害。因此有必要对砌体墙的抗爆性能作更深入的研究。
爆炸荷载主要受爆炸比例距离Z控制,其中Z=R/W1/3,R为爆心至结构的距离,W为炸药的TNT当量。Orton等[3]通过对前人工作的总结,指出对于墙板一类的构件:比例距离Z≤0.4 m/kg1/3属于近区爆炸;0.4 在砌体墙抗爆性能的研究方面,Varma等[5]对27面3 m×3 m的普通黏土砖墙进行了爆炸试验。研究了当比例距离2.2≤Z≤4.4 m/kg1/3和1.0≤Z≤2.0 m/kg1/3时,黏土砖墙的动力响应和损伤破坏模式,得到了墙体损伤等级与爆炸冲量的依赖关系。Wei等[6]基于Varma等的试验,依据墙体最大挠度以及墙端支座转角与墙体厚度的关系,提出了一种定量的划分墙体损伤等级的方法,并进行了相关数值模拟验证工作,分析了砂浆及砌块材料强度,边界锚固条件和墙厚等参数的影响。范俊余等[7]通过开展比例距离1.8≤Z≤10.0 m/kg1/3的12发爆炸试验,研究了普通黏土砖墙抗爆性能,探讨了爆炸荷载作用下墙体的破坏模式以及碎片的飞散和分布情况,并通过精细化有限元模型进一步探索了墙体裂缝的发展过程、墙体边界条件对破坏模式的影响以及墙体损伤程度与装药量的关系。Michaloudi等[8]基于RHT材料模型以及node-split算法进一步完善了普通黏土砖墙抗爆分析的有限元数值模拟方法,并通过开展当量为0.25 kg的接触爆炸和比例距离为Z=3.91 m/kg1/3的爆炸试验,验证了上述模型预测接触及远区爆炸下墙体局部破坏与碎片飞散的适用性。Shi等[9]通过开展Z=0.40 m/kg1/3和Z=0.22 m/kg1/3的两发爆炸试验,研究了普通黏土砖填充墙在近区爆炸作用下的局部破坏及碎片分布。 此外,美国空军实验室[10-13]针对混凝土空心砌块墙以及喷涂式聚脲加固砌体墙的抗爆性能开展了系统的试验和数值模拟工作,验证了聚脲加固的有效性并遴选出最优的聚脲加固材料,进一步讨论了聚脲材料性能参数及门窗开洞等对墙体抗爆性能的影响。基于上述工作,Moradi[14]进一步给出了爆炸荷载作用下砖墙动态响应计算的单自由度简化理论模型,能较准确地预测远区爆炸荷载作用下墙体的动态响应,但无法考虑墙体的局部损伤破坏。王军国等[15-16]在国内较早开展了聚脲加固黏土砖墙的爆炸试验和数值模拟,探究了墙体在不同支撑及加固条件下的抗爆性能、失效模式以及可承受的爆炸超压峰值。 常见的汽车炸弹和自杀性人体炸弹恐怖袭击大多属于近区爆炸。相较远区爆炸,近区爆炸下墙体主要发生局部破坏且更易形成砌块碎片,对建筑物内部人员和设备安全威胁更大。然而已有砖墙抗爆性能研究工作主要集中在Z>1 m/kg1/3的远区爆炸范围,仅Shi等开展了近区的黏土砖填充墙抗爆试验。同时,墙体抗爆试验成本高昂且结果离散度较大,数值模拟是该问题研究的有效补充。此外,爆炸荷载计算也是近区爆炸的研究难点,现有的经验计算公式通常无法在此范围得到较高精度的预测结果,需要进一步探索有效的爆炸荷载施加方法以研究近区爆炸时墙体的动态响应。最后,现实中常用砌块种类繁多,而关于这些砌块力学性能的研究,尤其是一些动力性能参数的确定,仍不全面。 本文基于Shi等的近区爆炸试验,采用商用有限元分析软件LS-DYNA[17],分别采用Load Blast法、任意拉格朗日欧拉(arbitrary Lagrange-Eulerian,ALE)法及冲量法三种方法开展了近区爆炸作用下黏土砖墙损伤破坏和动态响应的数值模拟。通过与试验中作用在墙体的爆炸冲击波超压以及墙体的损伤破坏进行对比,分析了上述方法的适用性。并进一步讨论了近区爆炸下爆炸距离、砌块砂浆的界面黏结强度以及砌块材料数值本构模型的影响。 如图1(a)所示,爆炸试验对象为钢筋混凝土框架内的两面高1.5 m、宽1.2 m、厚0.24 m的黏土砖填充墙。采用的M5砂浆厚10 mm,MU15砌块尺寸为240 mm× 115 mm×53 mm。墙体和框架上设置4个超压传感器(Pre 1~Pre 4)用以记录作用在墙体的反射超压荷载。共开展两次试验,其中TNT炸药的爆炸距离为0.4 m,正对墙体中心点放置。装药量分别为1 kg(试验1:Z=0.40 m/kg1/3,R/Rw=8.63)及6 kg(试验2:Z=0.22 m/kg1/3,R/Rw=4.75),满足Orton等与Henrych等关于近区爆炸的定义。 (a) 试验布置 图1(b)、(c)分别给出两次试验后墙体的损伤破坏情况。试验1中墙体正面中心部分砖块被压碎,形成尺寸为37 cm×19 cm×4 cm的对称粉碎性损伤区域。爆炸波传至墙体后在背面产生较大的拉应力,使砖块受拉剥离,其受损区域大小约为36 cm×33 cm×10 cm。试验2中墙体损伤更为严重,墙体中部被炸穿,正面开洞尺寸为60 cm×53 cm,背面开洞尺寸为93 cm×92 cm。两发试验中,由于传感器大多损坏,仅试验1中测得测点4的完整超压曲线和各测点超压峰值。 砌体墙的数值模型主要分为均质化和分离式两种。由于组成砖墙的砌块和砂浆材料力学性能差异较大,两者间的黏结界面往往是结构的薄弱层。将砌块与砂浆分开处理建立分离式精细化模型,尽管相对计算量较大,但能更好地反映砌块与砂浆间的黏结滑移与破坏过程。基于LS-DYNA有限元软件,本文采用8节点的六面体实体单元,建立了墙体的分离式精细化模型,如图2所示。Davidson等在模拟混凝土空心砌块墙体时,砌块单元尺寸约为16 mm,砂浆则为单层单元,模拟结果证明了这种网格划分尺寸的有效性。尽管更高精度的网格可以更精确地反映局部的破坏,但综合考虑到计算效率,本模型中砌块及墙体外部框架单元尺寸均取20 mm,砂浆厚度不足20 mm,采用单层实体单元,共计15.2万个单元。 图2 墙体有限元模型Fig.2 Finite element model of wall 考虑到砌块之间以及砌块与混凝土框架之间均采用砂浆填充,因此砌块与砂浆以及砌块与外部混凝土框架之间的接触采用关键字*TIEBREAK-SURFACE-SURFACE描述,其失效准则如下 (1) 式中:fn和fs分别表示接触面上的计算正应力和剪应力;Fn和Fs则表示接触面上的允许正应力及剪应力。上述接触方式可以较好地反映墙体中砌块与砂浆间的滑移及拉伸剪切失效。其中静摩擦因数FS取0.8,动摩擦因数FD取0.6。式(2)和式(3)分别为文献[18]中给出的砖砌体沿通缝弯曲抗拉强度平均值ftm,m和抗剪强度平均值fv,m的计算方法,其中f2为砂浆抗压强度平均值。TIEBREAK接触中允许正应力Fn和允许剪应力Fs的控制参数分别为NFLS和SFLS,据此取0.3 MPa。 (2) (3) 为了更好地模拟墙体在爆炸荷载作用下的损伤破坏并防止单元畸变,引入单元删除准则。考虑到过多的删除会导致结构能量与质量不守恒使得结果出现偏差,而砌块强度远高于砂浆且墙体的损伤主要沿砂浆层发展,故仅在砂浆模型中加入了*MAT_ADD_EROSION关键字,并以单元最大主应变项MXEPS作为失效准则,取值0.005。需要指出的是单元删除算法和失效应变的取值缺乏相关的物理基础和理论依据,本文主要通过试算确定。 砌块和砂浆都属于类混凝土的脆性材料,采用96号MAT_BRITTLE_DAMAGE模型。该模型是一种用于混凝土材料的各向同性的脆性损伤模型,适用于高应变率加载条件。其中,砌块和砂浆的抗压强度根据原试验中测得的砌块和砂浆平均抗压强度,分别取15.5 MPa和4.9 MPa。文献[19-20]给出了根据大量试验数据拟合得到的砌块弹性模量Eb和砌块平均抗压强度f1的经验公式(式(4)),以及砂浆弹性模量Em和砂浆平均抗压强度f2的经验公式(式(5)),砌块和砂浆的杨氏模量据此计算。其他参数主要根据文献[15]取值,详细模型参数取值如表1所示。 表1 砌块和砂浆材料模型参数Tab.1 Material properties for bricks and mortar (4) (5) 由于试验中的墙体外部结构并非单一框架,而是一个混凝土舱室,这使得外部结构的强度和刚度远高于砌体墙,并且试验结果也表明两次试验中外部结构几乎没有出现损坏。另外,本模型主要研究对象为墙体的损伤破坏和动态响应,建立外部框架主要是为了更好地模拟墙体的四边约束情况。因此考虑到计算效率的因素,将外部框架简化为刚体,采用MAT_RIGID模型,并限制其任意方向的旋转与位移。 本文主要通过Load Blast法、ALE法以及冲量法分别模拟了近区爆炸荷载作用。以下主要介绍三种荷载施加方法的具体实现过程。 2.3.1 Load Blast法 Load Blast法是LS-DYNA软件内置的一种基于CONWEP程序[21]施加爆炸荷载的常用方式。通过联合使用*LOAD_BLAST_SEGMENT以及*LOAD_BLAST卡片即可在选定的表面上施加爆炸产生的超压。在*LOAD_BLAST卡片中集成了地面和空中爆炸两种工况的爆炸超压计算经验公式,考虑到试验中装药高度相对墙体尺寸较高,因此按空爆类型计算,此时Load Blast法适用的比例距离范围为0.147~40.000 m/kg1/3,符合模拟工况要求。 2.3.2 ALE法 ALE法结合了Lagrange法和Euler法的优点,是一种用于解决流固耦合问题的常用方法。图3给出了基于ALE法的有限元模型,在原有的墙体模型上建立了TNT炸药、空气域和刚性地面的模型。其中空气及炸药使用尺寸为20 mm的ALE网格描述(*SECTION_SOLID_ALE)。刚性地面通过关键字*RIGIDWALL_PLANAR创建,空气域的其他边界设置为无反射边界(*BOUNDARY_NON_REFLECTING)实现半无限边界。炸药采用*MAT_HIGH_ EXPLOSIVE _BURN模型,其状态方程使用*EOS_JWL描述。空气材料采用*MAT_NULL模型,状态方程使用线性多项式*EOS_LINEAR_POLYNOMIAL描述,表2给出了相关参数取值。 图3 ALE法有限元模型Fig.3 Finite element model of ALE method 表2 TNT和空气材料模型参数Tab.2 Material properties for TNT and air 2.3.3 冲量法 冲量法是一种用于计算近场爆炸下结构响应的简化计算方法,通过直接施加速度(冲量)的方式模拟爆炸荷载。Henrych等给出了近区爆炸产生的比冲量计算公式 (6) (7) (8) (9) 再基于冲量定义,将其按下式除以所在位置的面密度即可求得所需施加的速度 (10) 在LS-DYNA软件中可以通过*SET_NODE_LIST将图示矩形等冲量线上节点建立点集,再采用*INITIAL_VELOCITY施加式(10)所得的速度,其分布如图4所示。 图4 计算示意图及冲量沿墙高分布示意图Fig.4 Diagrams of calculation and distribution of impulse 表3给出了试验1中实测和模拟得到的反射超压峰值。可以看出:采用ALE法施加爆炸荷载时,测点1和4处误差分别为14%和9%,可以较为准确地预测试验中各测点的反射超压峰值。而Load Blast法预测结果偏大,测点1和4处计算得到的超压峰值误差分别有47%和41%。 表3 试验1中各测点超压峰值对比Tab.3 Peak overpressure of each measuring point in test 1 MPa 图5给出了测点4处试验与模拟得到的完整超压时程曲线。需要说明的是由于试验中超压传感器存在触发时间,因此两种模拟方法得到的超压到达时间与试验结果存在差异。可以看出:ALE法模拟得到的反射超压时程与试验结果吻合较好,而Load Blast法预测得到的超压峰值更大,但是衰减得更快,作用在墙体上的冲量相对较小。 图5 试验1测点4反射超压时程Fig.5 Overpressure-time history of measuring point 4 in test 1 图6给出了三种荷载施加方法下得到的试验1墙体中心点的位移时程曲线。可以看出,1 kg装药时,三种方法预测结果相似,墙体基本处于弹性状态,仅产生微小的残余变形。 图6 三种荷载施加方法下试验1中墙体中心位移时程曲线Fig.6 Displacement-time histories of wall center in test 1 predicted by three simulation methods 图7分别给出了三种荷载施加方法模拟得到的试验1中墙体的最大主应变云图,其能较好地反映试验中得到的墙体局部损伤结果。可以看出:三种荷载模拟方式下,爆炸冲击波首先作用在墙体正面中心位置,随后在墙体背面边界和中心处集中出现较大的主应变。其中ALE法和冲量法模拟结果相近,正面中部主应变集中区域长宽约30 cm,沿厚度分布约6~8 cm。采用冲量法时,正面中部的主应变相对数值较小,沿厚度的分布较为分散,但较好地得到了墙体背面中部的主应变集中区域。Load Blast法由于预测的爆炸荷载更大,因此模拟到的主应变集中区域范围更大且更均匀,长宽约40 cm,沿厚度分布超过10 cm。 (a) Load Blast法 综上,在对试验1的模拟中,Load Blast法对于近区爆炸荷载的预测精度较差,而ALE法预测结果与试验数据吻合较好。通过对比墙体中心点位移时程和主应变云图,三种荷载施加方法得到的墙体动态响应相近。尽管冲量法在施加荷载时比较繁杂且无法得到墙体上的反射超压,但其计算量得到极大简化,相比ALE法计算时间可缩短数十倍。 图8给出了6 kg TNT当量的试验2中,不同爆炸荷载施加方法得到的墙体最终变形和中心点位移。可以看出:① Load Blast法虽然也可以得到集中于墙体中部的损伤,但由于其预测的爆炸荷载较大、分布更均匀,导致破坏范围过大,墙体整体式破坏的趋势;② ALE法预测结果中,墙体中部被炸穿,正面形成了高约90 cm、宽约70 cm的局部孔洞,墙体背面孔洞高约90 cm、宽约80 cm,孔洞形状介于菱形与圆形之间,破坏主要沿砂浆层发展;③ 冲量法预测结果中墙体中部同样出现了范围较大的局部孔洞,在正面和背面形成了高约80 cm、宽约70 cm的近似矩形的破坏区域。尽管损伤区域尺寸仍有一定误差,但总体与试验结果吻合较好。从三种方法模拟得到的侧剖面可以明显看出墙体砌块在爆炸作用下的飞散情况。 (a) Load Blast法 图9分别给出了不同爆炸荷载施加方法模拟得到的6 kg装药下墙体中点沿墙面法向的位移时程曲线和速度位移时程曲线。可以看出三种方法模拟得到的位移和速度曲线存在微小偏差,但总体相近。其中冲量法模拟得到的结果相对较小。而Load Blast法模拟得到的位移和速度曲线在初始时刻较大,但随后低于ALE法。 图9 三种荷载施加方法得到的试验2中墙体中心位移时程曲线和速度时程曲线Fig.9 Displacement-time histories and velocity-time histeries of wall center in test 2 predicted by three methods 此外,从图9中墙体中点位移时程曲线可以看出,在接近30 ms时,三种方法模拟得到的墙体中点速度都逐渐平稳在15 m/s左右,这表明墙体中部的砌块出现了飞散。根据墙体中点高度,可以计算出墙体中点约在0.4 s坠地,并由图9中的位移和速度时程曲线进一步估算ALE法、冲量法和Load Blast法模拟得到的墙体中点最终飞散距离,分别为6.83 m,6.42 m和6.57 m。尽管与试验得到的碎片最大飞散距离较大,但碎片生成的过程中存在一定偶然性,抛散距离最远的碎片不一定来自墙体中点,另外由于爆炸中可能使碎块产生向上的速度,从而使得砌块下落时间增长,抛散距离变大。通过与图10试验得到的试验2中碎片飞散距离的统计数据对比,由模拟估测的墙体中点飞散距离超过了近90%的粗粒径碎片,以及85%左右的细粒径碎片。考虑到墙体中点通常能有较大的抛散速度,结合以上分析,可以认为三种模拟方法对近区爆炸下墙体碎片飞散的模拟是有效的。 图10 试验得到的试验2中碎片飞散距离统计图Fig.10 Mass proportions of fragments in total mass at different splash distances in test 2 综合上述比较可以得出,三种爆炸荷载施加方式都能模拟出近区爆炸下墙体的局部破坏和碎片飞散。但相比于Load Blast法,ALE法和冲量法对于墙体破坏形态的模拟与试验结果更为接近,考虑到计算效率的因素,冲量法可以作为一种模拟近区爆炸荷载作用的较优方法。另外需要指出的是对于损伤区域的具体尺寸和损伤程度,尤其是墙体背面损伤情况,模拟结果与试验还存在着一定的误差。一方面是由于砖墙抗爆试验本身通常具有较高的离散性;另一方面,砌块和砂浆的部分材料参数还需要更精确的测定,更重要的是现有的可用于模拟砌块与砂浆的材料模型仍具有较大的局限性,缺少模拟砌块碎裂有效方法,对模拟结果造成了较大的影响。 本章进一步讨论了当比例距离一定时,炸药爆炸距离、砌块砂浆界面黏结强度以及砌块材料数值模型对近区爆炸作用下墙体损伤破坏和动态响应的影响。 为探究在相同比例距离下墙体的损伤模式是否具有一致性,通过改变爆炸距离与当量,进一步补充了比例距离为0.40 m/kg1/3和0.22 m/kg1/3时,爆炸距离为0.3 m,0.5 m以及0.6 m的6组工况,详见表4。图11给出了比例距离为0.4 m/kg1/3时,墙体中点的位移时程曲线,此时墙体响应均处于弹性状态,但随着爆炸距离的增大,墙体中心点处的最大挠度以及残余变形逐渐加大,但结构的破坏模式总体没有发生变化。 图11 比例距离0.40 m/kg1/3时不同爆炸距离下墙体中心点位移时程曲线Fig.11 Displacement-time histories of wall center under various standoff distance and identical scaled standoff distance of 0.40 m/kg1/3 表4 不同爆炸距离工况下墙体的损伤程度Tab.4 Damage of wall for different standoff distances 图12给出了当比例距离为0.22 m/kg1/3时,冲量法模拟得到的不同爆炸距离下砌体墙的破坏形态。可以看出墙体破坏模式都主要沿墙体中部向四边发展,并随着爆炸距离的增大破坏加剧。随着爆炸距离的增加,明显出现两类破坏形态:在0.3 m和0.4 m爆炸距离时,主要表现为墙体中部被炸穿,以局部破坏为主;而在0.5 m和0.6 m爆炸距离时,墙面因爆炸产生的洞口进一步扩大,最终引起了墙体整体式破坏。 图12 比例距离0.22 m/kg1/3时不同爆炸距离下墙体破坏形态Fig.12 Damage of wall under different standoff distance and identical scaled standoff distance of 0.22 m/kg1/3 图13分别给出了在比例距离Z=0.40 m/kg1/3和Z=0.22 m/kg1/3时,基于式(6)积分得到的墙面受到的总冲量随着爆炸距离改变,与墙体中点位移峰值或0.03 s时飞散距离的关系图。可以看出在比例距离相同的情况下,随着爆炸距离增加,作用于墙面的总冲量也随之增加,从而导致墙体中心位移随之变大,且两者间存在近似线性的关系。 (a) Z=0.40 m/kg1/3 图14进一步给出比例距离为0.22 m/kg1/3时,ALE法得到的不同爆炸距离下的墙面超压分布云图。可以看出,由于比例距离不变,随着爆炸距离的增加,炸药量相应增加,墙体边缘承受的超压增加幅度更大,墙面上整体的超压分布愈趋平均,因此导致墙体破坏模式趋于整体破坏。 图14 比例距离0.22 m/kg1/3时不同爆炸距离下墙面超压分布Fig.14 Overpressure contour of wall under different standoff distance and identical scaled standoff distance of 0.22 m/kg1/3 上述分析表明:近区爆炸下,墙体的破坏形态以局部破坏为主,但通过分析墙面超压分布和墙面总冲量与墙体中点位移峰值或飞散距离的关系,在比例距离不变的情况下增大爆炸距离,会使墙体表面所受超压趋于平均,同时墙面上总冲量值增加,使得墙体的破坏愈加严重并趋于整体坍塌的破坏模式。因此,近区爆炸下墙体的破坏形态不仅与比例距离有关,还与爆炸距离关系密切。 前述模型中主要通过采用TIEBREAK接触模拟墙体砌块与砂浆的界面黏结,其主要控制参数为NFLS和SFLS,取值皆为0.3 MPa。本节通过改变上述参数取值,模拟不同砌块砂浆的界面黏结强度对墙体抗爆性能的影响。表5给出了1 kg和6 kg TNT装药下的各计算工况。 表5 考虑不同砌块砂浆界面黏结强度的各工况Tab.5 Discussed scenarios with different bonding strength between brick and mortar 图15给出了各种工况下墙体中心点的位移时程曲线,可以看出在1 kg及6 kg装药的情况下,随着NFLS和SFLS值增大,墙体中心点位移逐步减小。图15(a)、(d)中单独增加NFLS的情况下,墙体中点位移峰值减小幅度不显著,1 kg和6 kg装药下减小幅度分别为0.5%和2.7%。图15(b)、(e)中随着SFLS取值变化,墙体的位移变化相对明显。尤其是1 kg装药的情况下SFLS由0.3增加为0.6时,墙体中心点位移峰值减小了5.2%。说明墙体在承受爆炸荷载时,砌块与砂浆间的切向失效应力起主要作用。另外,在图15(c)、(f)中,当同时增大或减小NFLS和SFLS时,墙体中心点位移变化幅度较大,如在6 kg装药下墙体中心点位移峰值变化幅度达到了8.5%。 (a) 1 kg装药 单独改变NFLS取值 图16 不同砌块材料模型下的墙体中心点位移时程曲线Fig.16 Displacement-time histories of wall center with three masonry brick models (a) MAT_WINFRITH_CONCRETE模型 综上所述,近区爆炸作用下,墙体的变形和位移随着砌块与砂浆界面黏结强度增强而降低,其中切向失效应力起主要控制作用。这表明墙体在近区爆炸下的破坏趋于冲切型破坏,抵抗爆炸作用时砂浆与砌块间的剪切力起了主要作用。随砌块砂浆界面剪切强度的提升,耗散的墙体中因爆炸产生的能量也随之增加。但模拟结果也表明这种耗散作用有限,对墙体整体抗爆性能的提升有限。 LS-DYNA软件中有多种适用于模拟砌块材料的数值本构模型,本节进一步选取MAT_WINFRITH_ CONCRETE和MAT_SOIL_AND_FOAM讨论三种砌块材料数值模型的适用性。上述两种数值模型的主要参数主要根据文献[12]取值,详见表6和表7。 表6 MAT_WINFRITH_CONCRETE材料模型参数Tab.6 MAT_WINFRITH_CONCRETE model parameters 表7 MAT_SOIL_AND_FOAM材料模型参数Tab.7 MAT_SOIL_AND_FOAM model parameters 图16给出了1 kg装药下三种不同材料模型得到的墙体中心点位移时程,可以看出:MAT_WINFRITH_ CONCRETE和MAT_SOIL_AND_FOAM模型预测的峰值位移分别较MAT_BRITTLE_DAMAGE模型预测结果分别大54.2%和41.2%,相应30 ms时刻的残余变形分别大182%和283%。图17分别给出了6 kg装药时的MAT_WINFRITH_CONCRETE和MAT_SOIL_AND _FOAM模型预测的墙体最终破坏情况。可以看出:两种模型预测结果均比MAT_BRITTLE_DAMAGE模型(图10)得到墙体破坏结果更为严重。其中MAT_SOIL_AND_FOAM得到的结果趋于整体破坏,与试验结果偏差较大。而MAT_WINFRITH_ CONCRETE模型预测结果与试验吻合更好,尤其是墙体背面的破坏范围,其原因主要在于上述材料模型的损伤定义存在差异。另外需要指出的是黏土砖材料的动力性能参数的确定工作仍有待进一步完善。 本文围绕砌体填充墙在近区爆炸作用下的损伤破坏和动态响应问题,基于已有钢筋混凝土框架黏土砖填充墙的近区爆炸试验开展了数值模拟分析,主要工作和结论如下: (1) 通过对比模拟近区爆炸荷载作用的三种方法得出:Load Blast法预测的爆炸荷载峰值较高,沿墙面分布更均匀,模拟得到的墙体破坏程度更高,对墙体局部破坏的模拟相对较差;ALE法能较好地模拟出墙体破坏形态,更为准确地得到近区爆炸下墙体上的反射超压值,但计算效率低;冲量法无法预测超压荷载,但可以在较好地模拟墙体破坏的同时兼具较高的计算效率。另外,试验中墙体背面砌块剥离现象仍无法较好重现,有待进一步完善。 (2) 近区爆炸作用下,墙体以局部破坏为主,相同比例距离下,但随着爆炸距离增大,墙体的破坏程度加剧并趋于整体坍塌破坏。因此,近区爆炸下墙体的最终破坏形态还与爆炸距离密切相关,在评估墙体损伤程度时,应综合考虑爆炸距离和比例距离的共同影响。 (3) 墙体抗爆性能与砌块砂浆的界面黏结强度正相关,砌块与砂浆间的剪切失效应力较轴向失效应力起更主要的控制作用,但对于墙体抗爆性能的影响相对有限。 (4) 砌块本构模型对墙体损伤破坏与动态响应影响较大,MAT_WINFRITH_CONCRETE和MAT_ BRITTLE_DAMAGE能较好重现近区爆炸下墙体的局部损伤程度和破坏模式,然而砌块材料模型参数的确定尚需要进一步系统的工作。1 试验简介

2 数值模拟
2.1 有限元模型
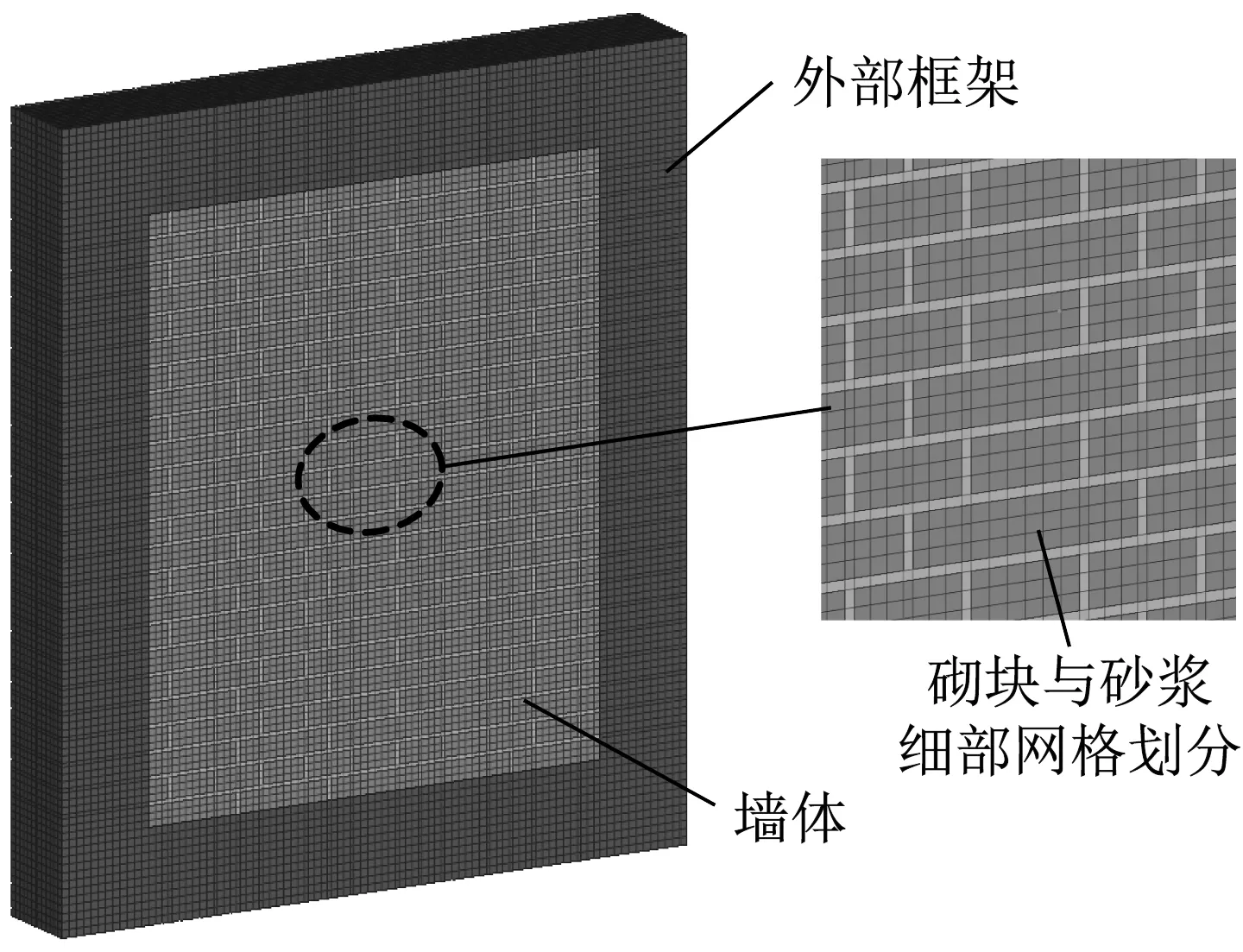
2.2 材料模型和参数

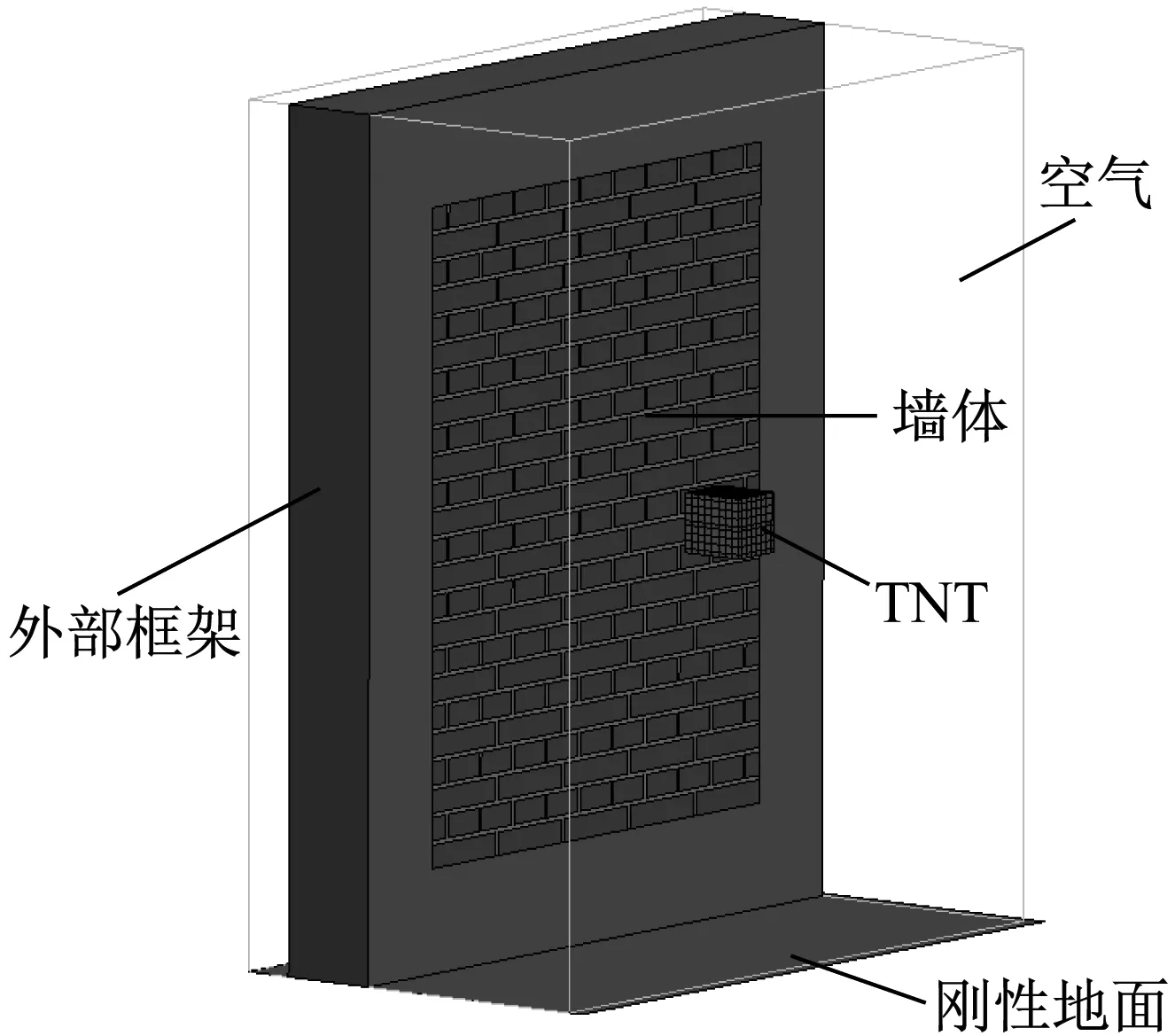
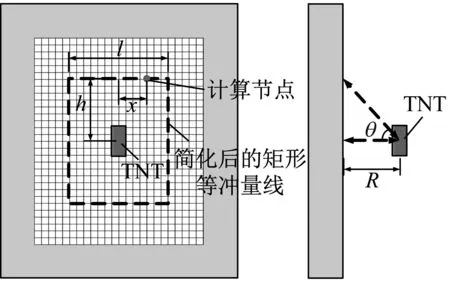
2.3 荷载施加方法

3 结果对比

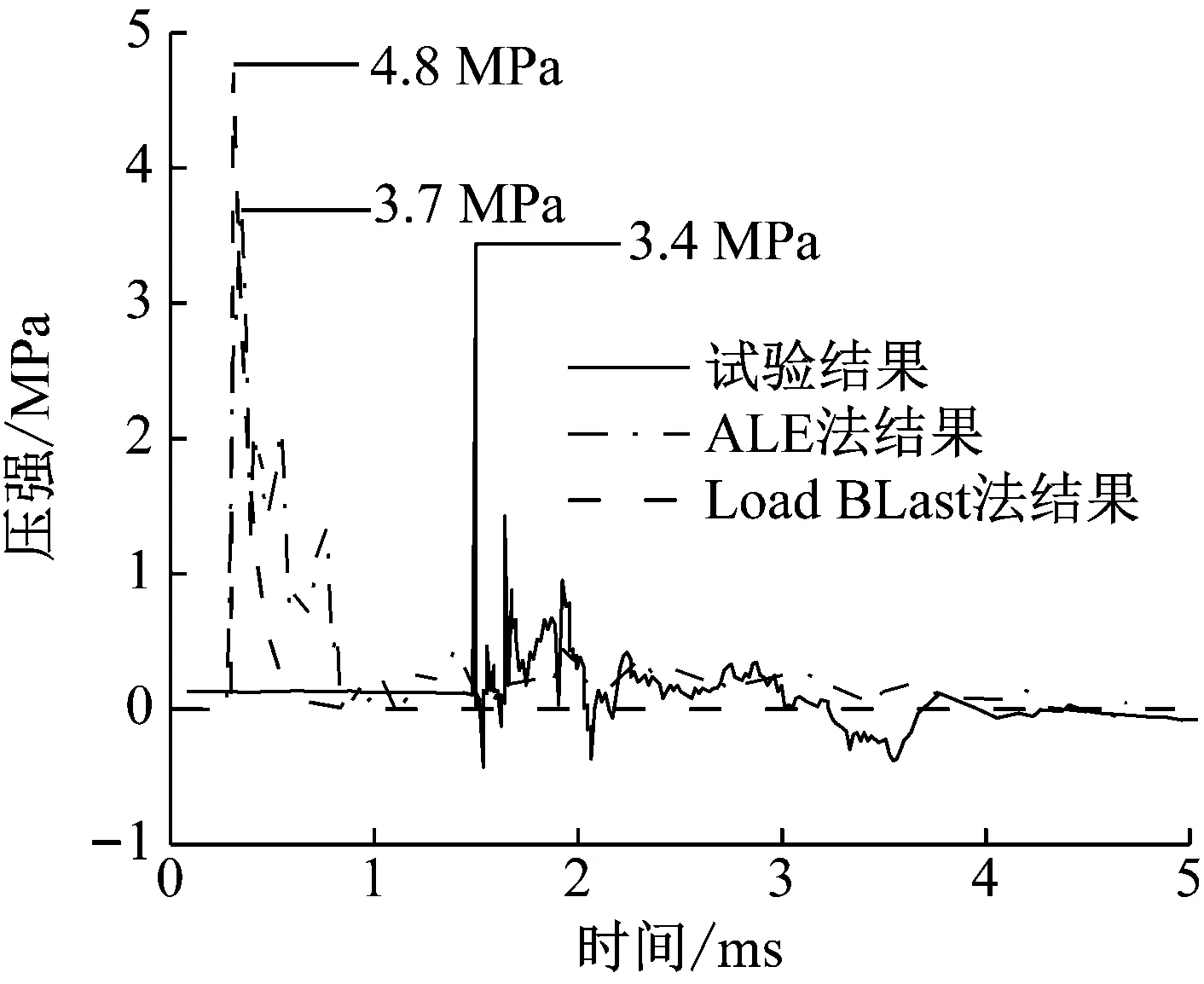
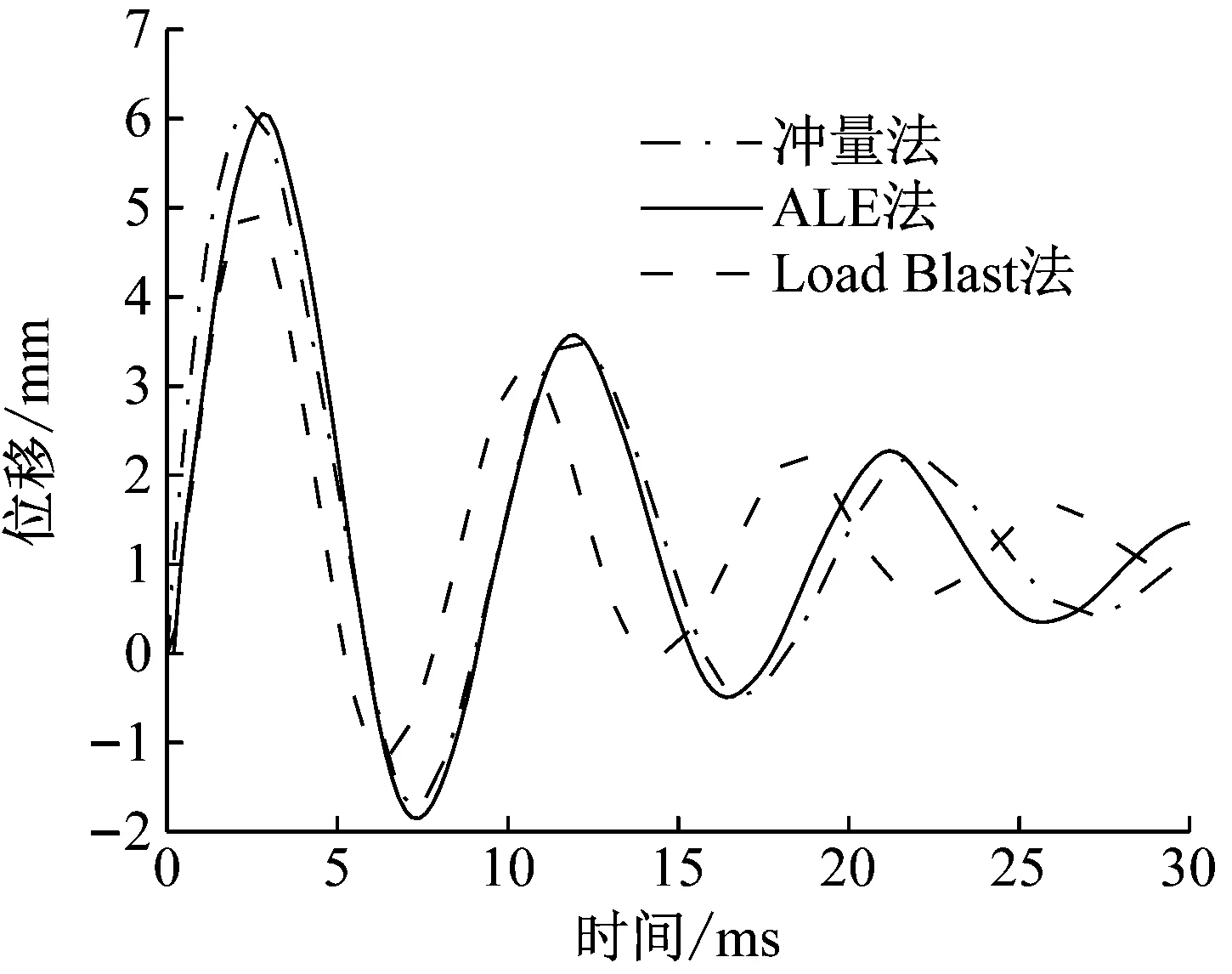


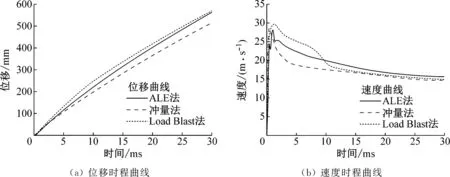
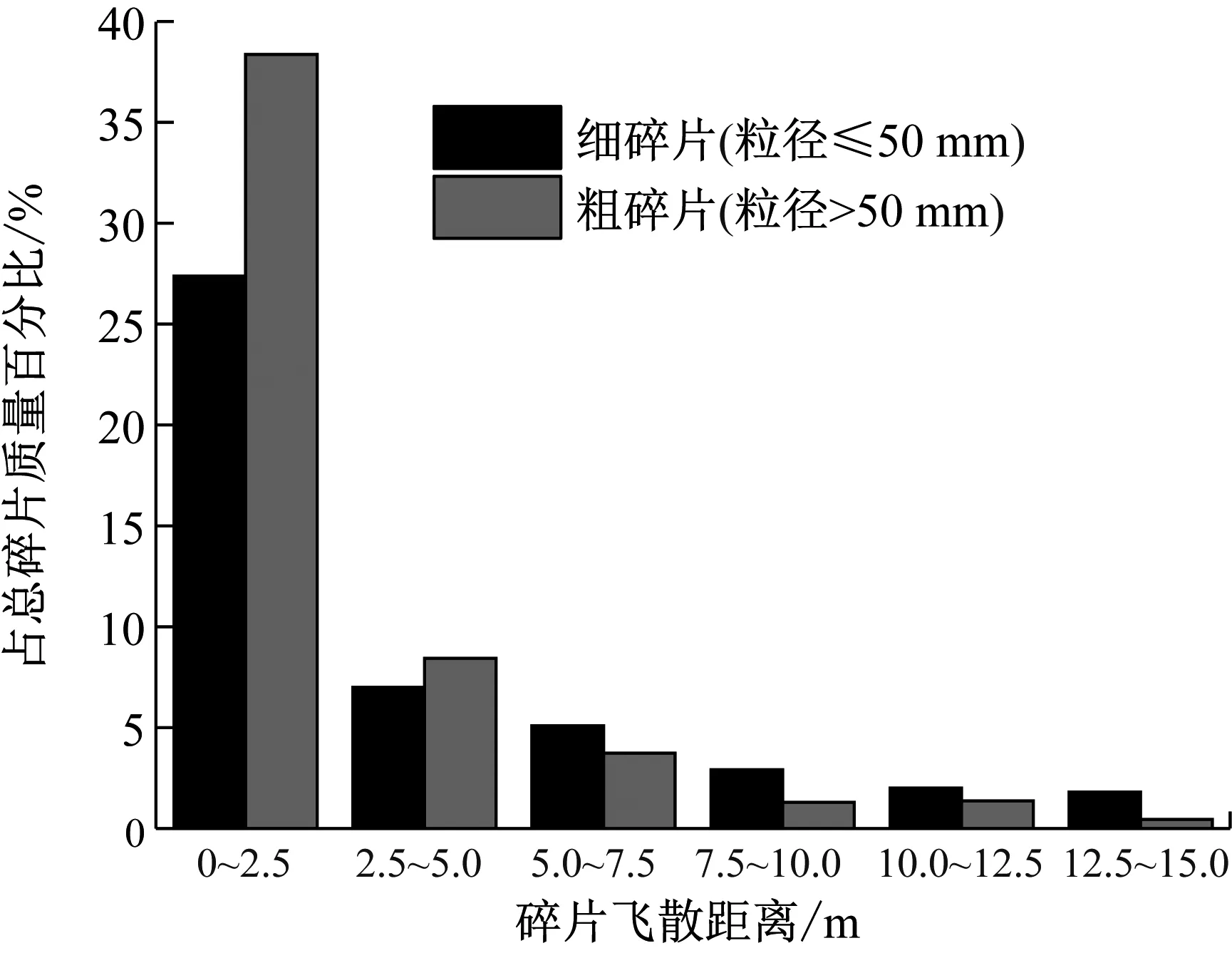
4 参数影响分析
4.1 爆炸距离

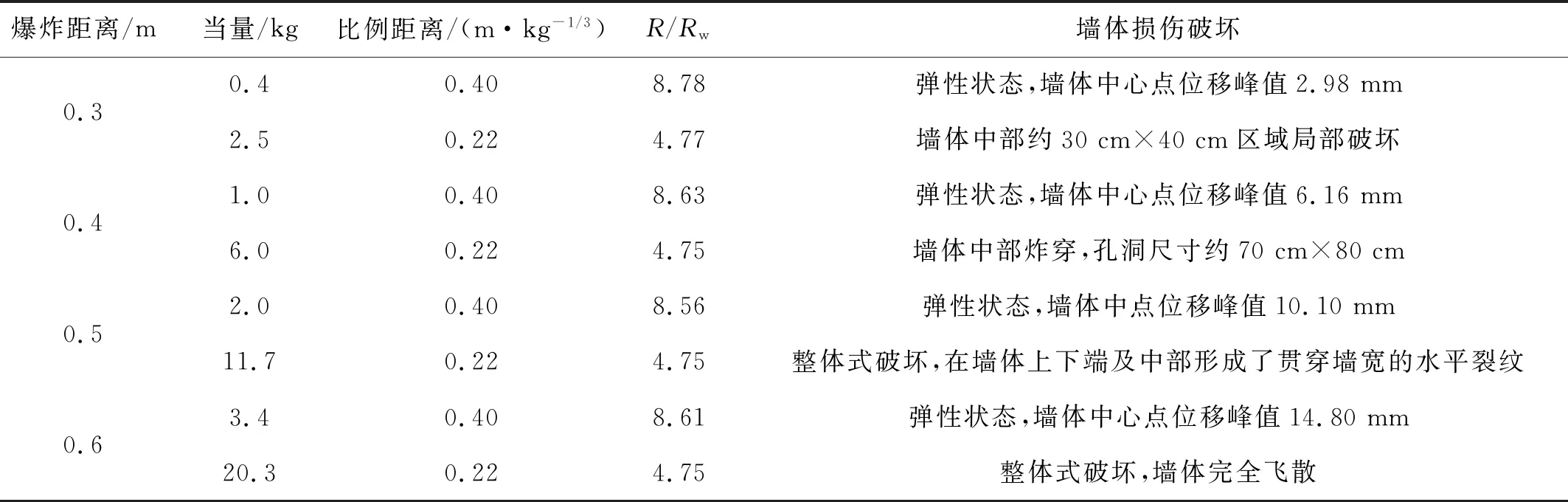

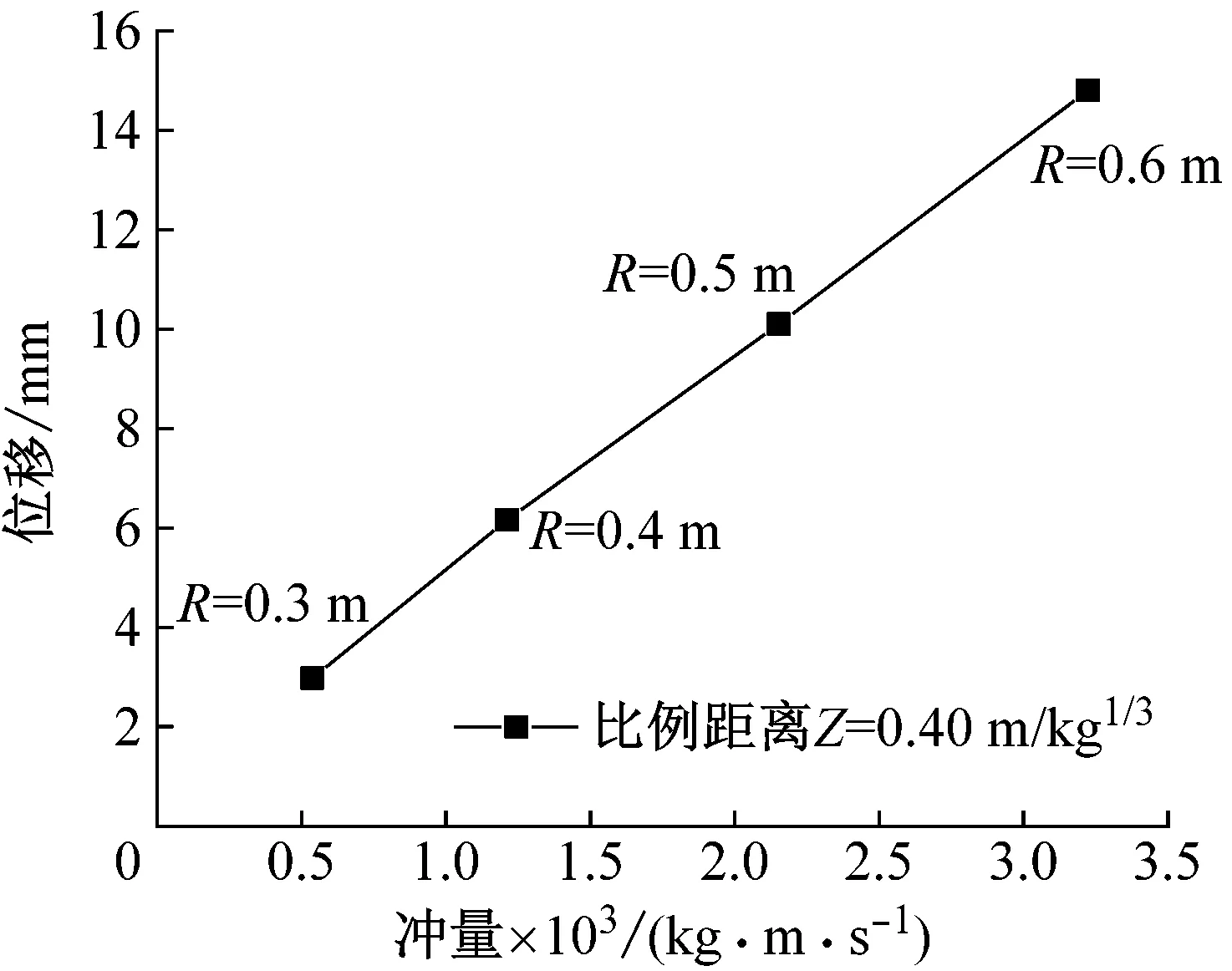

4.2 砌块砂浆界面黏结强度
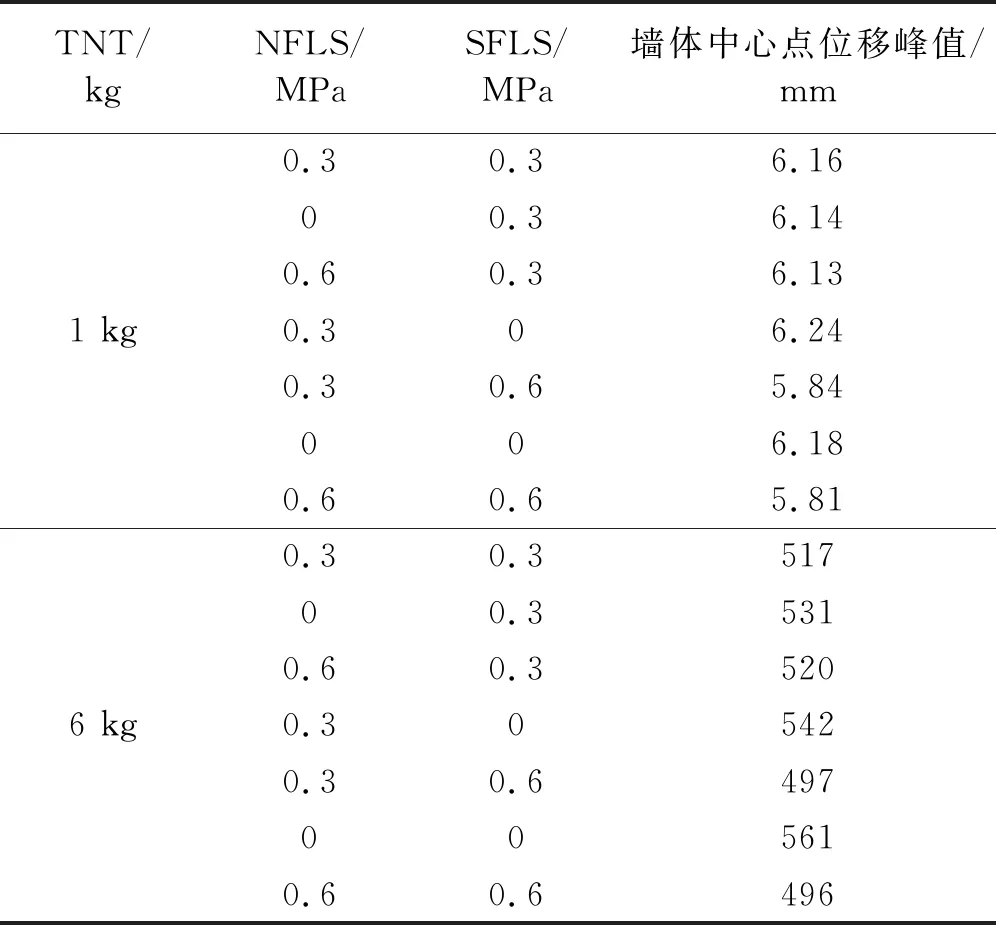
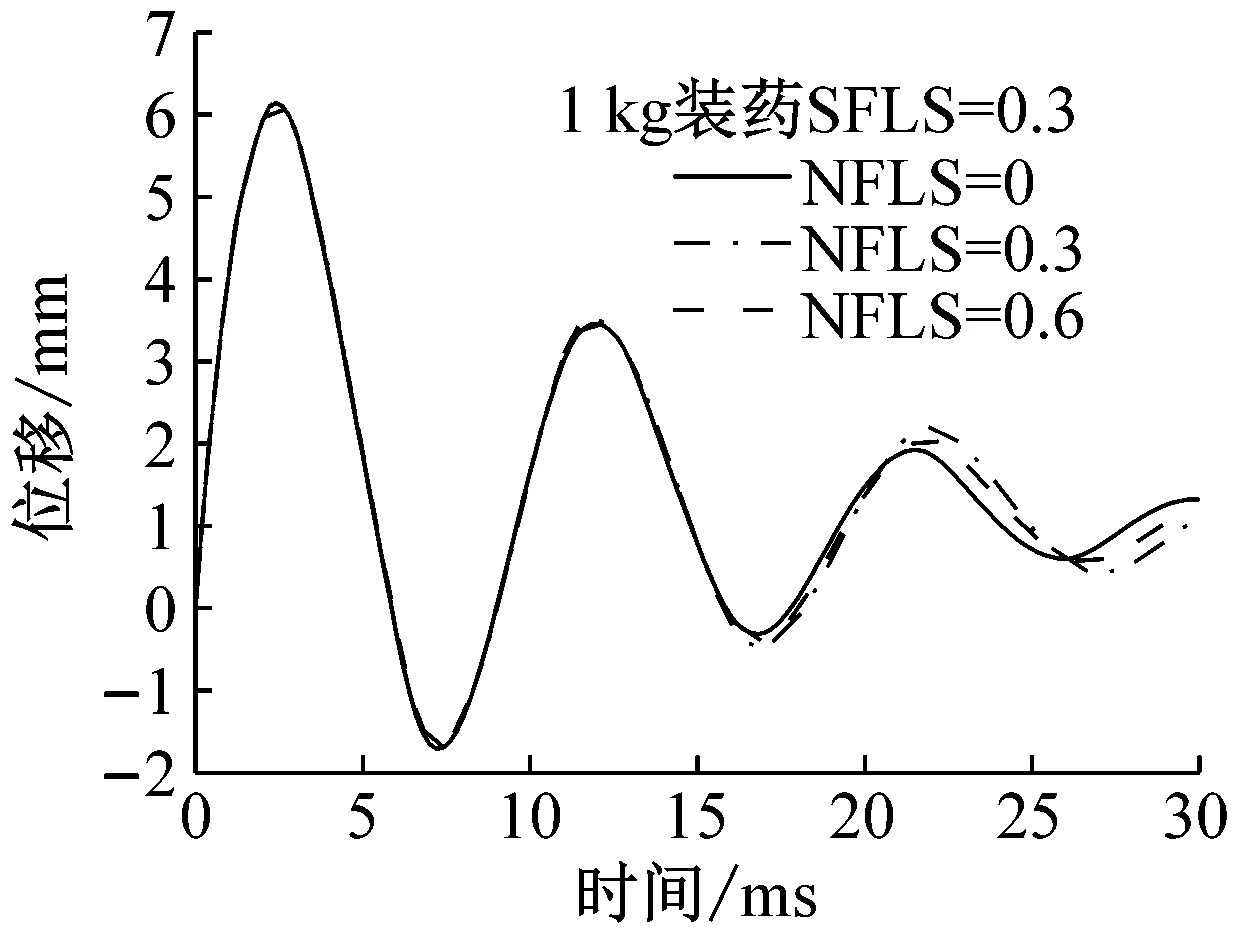
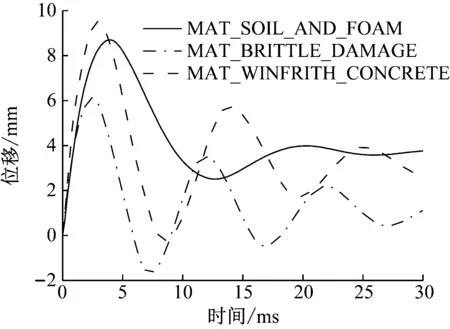

4.3 砌块材料模型


5 结 论
