分流气体对冲排气消声器气流再生噪声模型研究
2021-05-17张海军宗哲英张永安
张海军,苏 赫,武 佩,宗哲英,张永安,薛 晶
(内蒙古农业大学 机电工程学院,呼和浩特 010018)
目前,内燃机仍是交通运输的主要动力装置,其使用已遍布交通运输和工农业生产的各个方面[1]。但内燃机较为突出的缺点是排气噪声大,而降低内燃机排气噪声最直接有效的方法就是安装排气消声器[2]。气流再生噪声与消声性能密切相关,是评价消声器性能的一项重要指标[3]。近年来,国内外学者对消声器气流再生噪声进行了大量研究[4-7]。Desantes等[8]研究了直管、突然收缩和简单扩张腔三种结构的排气消声器气流再生噪声,获得了结构参数和气流速度与气流再生噪声的关系。Jebasinski等[9]研究了穿孔管排气消声器结构参数变化对气流再生噪声的影响,得到在给定孔的大小和形状的情况下,斯德鲁哈尔数的范围不依赖于穿孔形式和穿孔率的结论。English等[10]以膨胀腔消声器为研究对象,采用试验和相关声能量流分析法,对气流再生噪声源频率特征及气流再生噪声与腔体几何形状之间的关系进行了研究,发现尾管对气流再生噪声的影响显著。赵海军等[11]根据相似理论和量纲分析法建立了关于湍涡耗散分布特征系数的穿孔板消声器气流再生噪声总声功率级模型,得到了消声器进口管直径、穿孔板距离和厚度、穿孔直径、扩张比、穿孔率及气流速度对气流再生噪声总声功率级的影响规律。以上研究为消声器气流再生噪声模型研究提供了重要思路,但对基于结构参数和气流速度的气流再生噪声模型研究及参数间交互作用对气流再生噪声的影响规律研究少见报道。
本文以基于气流反相对冲以降低气流速度为主的新型分流气体对冲排气消声器为研究对象,对其气流再生噪声模型进行研究。在前期的研究中,对该新型消声器行了理论计算、数值模拟和试验验证等[12-14],证实了该消声器的可行性和优越性。在气流再生噪声方面,霍黎明等[15]运用FW-H(Ffowcs-Williams and Hawkings)声学比拟法对该新型消声器内部选定点的噪声进行了研究,发现噪声的能量主要集中在低频段,且在低频段,随着频率的升高,噪声声压级呈现降低趋势;频率在2 kHz以上的噪声呈现宽频特性;测点噪声总声压级与湍动能呈正比关系。但关于结构参数和气流速度对气流再生噪声的影响规律还未进行研究。
气体与固体结构表面的相互作用以及湍流的存在是气流再生噪声的成因,而湍流是引起气流再生噪声的主因[16]。所以,本文基于计算流体动力学(computational fluid dynamics,CFD),只计算由湍流引起的气流再生噪声;首先,利用FW-H声学比拟法对消声器气流再生噪声进行数值计算,通过试验验证计算方法的准确性;其次,采用Design-Expert 8.0软件对气流再生噪声试验进行设计,对数据进行统计分析,建立气流再生噪声总声压级数学模型;最后,探讨消声器结构参数、气流速度及其交互作用对气流再生噪声总声压级的影响规律。
1 新型消声器工作原理及模型计算理论
1.1 新型消声器工作原理
图1为分流气体对冲排气消声器工作原理图。当气流从入口流入,经锥形面导流后进入环形腔,然后进入A、B和C、D两组对冲孔形成速度大小相等、方向相反的两股对冲气流,两股气流在内腔中心相遇对冲而使气流流速降低,然后从尾管流出。
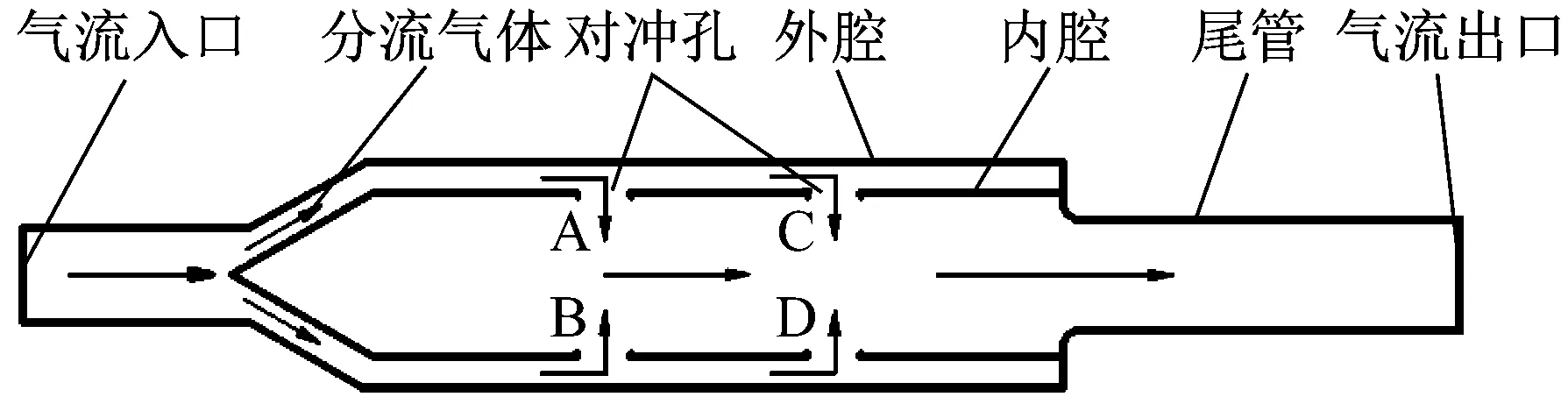
图1 分流气体对冲排气消声器工作原理图Fig.1 Principle of the split-stream rushing exhaust muffler
1.2 模型计算理论
1.2.1 CFD分析基础
CFD计算遵循质量、动量和能量守恒定律,假设消声器内流体为不可压缩流体,流体模型为湍流模型。流场控制方程采用雷诺时均N-S方程,连续性方程和N-S方程如式(1)和(2)所示。
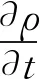
(1)
(2)
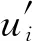
在CFD计算中,稳态流场计算的湍流模型选择标准k-ε湍流模型,k方程为精确方程,ε是由经验公式推导出的公式,k-ε方程参见文献[13];瞬态流场计算的湍流模型选择LES大涡模拟湍流模型。大涡模拟是对N-S方程中一些小涡进行过滤,小涡漩对湍流的影响用亚网格应力模型进行模拟,起主要作用的大涡漩通过非稳态的N-S方程直接进行求解,LES方程如式(3)和(4)所示
(3)
(4)
式中,τij为亚网格应力,它的物理意义为过滤掉的小尺度涡漩和尺度脉动间的能量交换。
1.2.2 CFD数值计算
使用Creo软件建立新型消声器三维几何模型,将其导入HyperMesh中生成流体区域的实体模型,采用适应性较强的四面体单元网格对其进行网格划分。将流体网格导入Fluent软件,首先采用基于稳态的Pressure-Based求解器,选择标准k-ε湍流模型,压力速度耦合方式选择SIMPLE进行稳态流场计算。数值计算稳定后,将稳态计算结果作为初始值,采用基于瞬态的Pressure-Based求解器,选择LES大涡模拟湍流模型,压力速度耦合方式选择FRACTIONAL STEP进行瞬态流场计算。进口气流速度为40 m/s时消声器XOY平面湍动能云图和声功率云图如图2所示。

(a) 湍动能云图
1.2.3 FW-H理论
Ffowcs-Williams和Hawkings考虑了壁面边界条件对于物体发声的影响,通过引入赫维塞函数H(f)和Dirac Delta 函数δ(f),从连续性方程和N-S方程推导,得到了考虑物体在流动介质中发声问题的FW-H方程[17-18],如式(5)所示
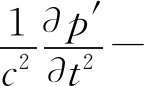
(5)
式中:c为远场声速;p′为远场声压;t为时间;Tij为应力张量;H(f)为赫维塞(Heaviside) 函数;Pij为压缩张量;nj为沿声源表面外法线的单位法向量;ui为在xi方向的流体速度分量;x为选定的声场坐标轴方向;ρ为流体密度;un和vn分别为垂直于积分面的流体速度分量和积分面移动速度分量;δ(f)为Dirac Delta函数;下标n、i、j分别表示沿固体声源外法线方向和选定的声场坐标系i、j方向;ρ0为远场流体密度;f=0 表示无边界空间流动的一个数学定义面,这个表面(f=0)为声辐射面。
通过两次面积分和一次体积分可对式(5)进行求解,单极子和偶极子声源可通过面积分计算获得,四极子声源可通过体积分计算获得。
2 气流再生噪声试验验证
2.1 试验方法
消声器气流再生噪声试验台测试系统包括YX-73D-2型2.2 kW高压风机、变频器、稳压器、消声器、美国TSI公司的9565-P多功能风量计和B&K公司的2250型手持噪声分析仪。在试验台上启动高压风机,在消声器入口分别施加速度为10、20、30、40、50和60 m/s的气流,测试测点的噪声声压级,测点为距消声器出口中心点为1 m、方向为与消声器水平中心线夹角成45°。
CFD数值试验,建立同样的模型施加相同工况,采用1.2.2节中的数值计算方法进行流场计算,流场计算稳定后,开启声学模块,采用FW-H声学比拟法计算分流气体对冲排气消声器选定测点的噪声。
2.2 验证结果
从现有分流气体对冲排气消声器中任选一种作为测试对象进行气流再生噪声试验和数值计算,所选消声器的内腔直径为70 mm、分流单元锥角为90°、对冲孔为矩形(矩形长边和短边长分别为45.2 mm和10 mm)、两组对冲孔中心距内腔两端的距离均为103.4 mm,对冲孔中心距为126 mm。
不同入口气流速度下CFD数值计算和试验台试验结果对比如图3所示。在入口气流速度为10~60 m/s时,气流再生噪声计算值和试验值相对误差分别为0.98%、1.99%、2.58%、3.11%、3.38%和4.23%,最大不超过5%。说明CFD数值计算结果有效、准确,可以为后续的流场计算提供依据。
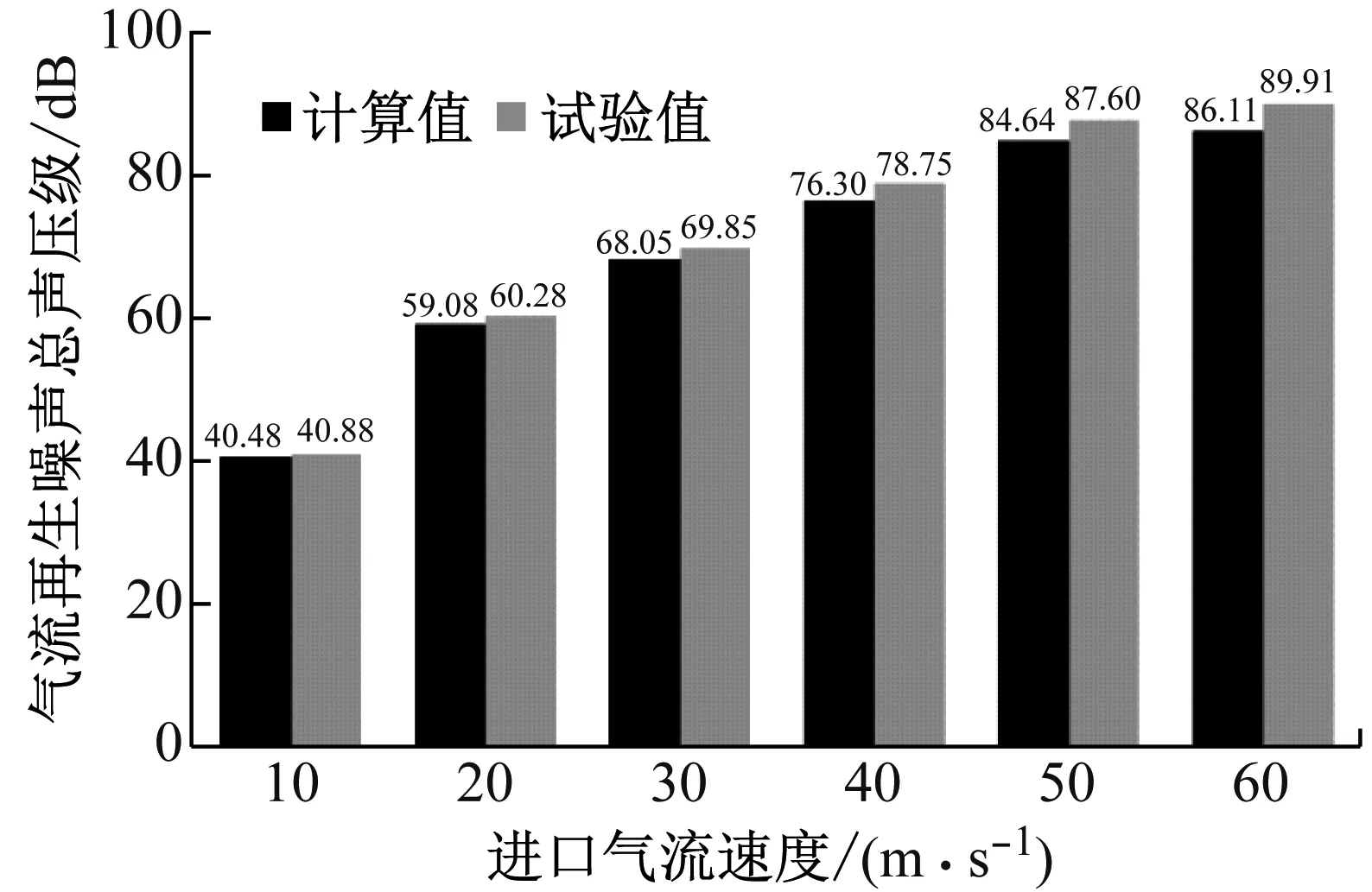
图3 不同进口气流速度下CFD计算值和试验值对比Fig.3 Comparison of CFD calculation with experiment under different inlet airflow velocities
3 试验设计及试验结果
3.1 试验对象
本文以CG25单缸柴油机为样机(该样机的气缸直径为115 mm、活塞行程为120 mm、额定功率为15.7 kW、标定转速为2 200 r/min、活塞排量为1.246 L、发动机排气管径为42 mm、压缩比为17.3),依据其主要技术参数,确定了分流气体对冲排气消声器主要结构尺寸参数,如图4所示,其中:D1=42mm、D2=70~90 mm、D3=100 mm、D4=50 mm、L1=638 mm、L2=95 mm、L3=100 mm、L4=518 mm、内腔分流单元锥角α1=30~90°、外腔分流单元锥角α2=90°、两组对冲孔的总流通面积1 808 mm2、对冲孔中心距为S、尾管过度圆弧R1=5 mm、消声器壁厚为1.5 mm。

图4 分流气体对冲排气消声器结构简图Fig.4 Schematic diagram of the split-stream rushing exhaust muffler
3.2 试验设计和试验结果
3.2.1 试验方法
本试验采用试验设计和专业响应面分析软件Design-Expert 8.0中的Box-Behnken响应面设计法进行试验设计,该方法是一种解决多变量问题的数学统计方法,常用于在因素和响应值之间存在多元非线性关系时寻找最佳试验条件。
3.2.2 试验因素及因素水平的确定
取气流再生噪声总声压级为试验指标,试验因素为内腔直径A、对冲孔形状B、对冲孔中心距C、内腔分流单元锥角D、气流速度E五个因素。采用五因素三水平Box-Behnken响应面分析法进行试验设计[19],试验因素及水平设置如表1所示。
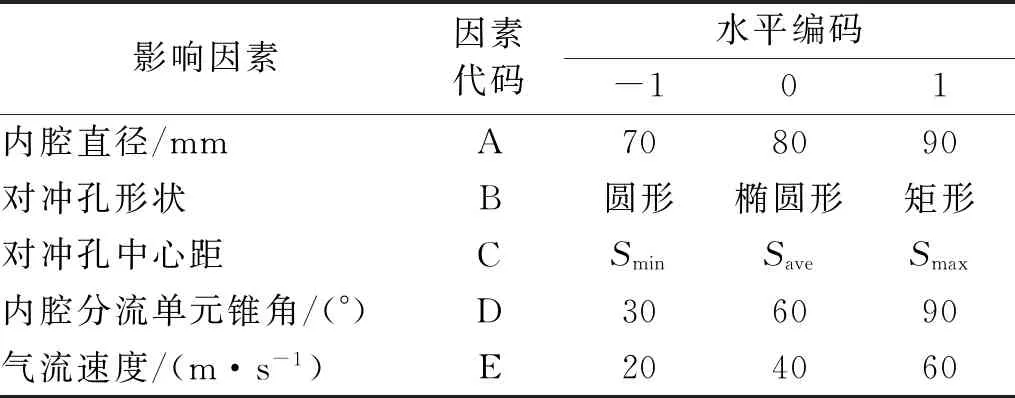
表1 试验因素及水平Tab.1 Factors and levels of experiments
其中因素B和C的水平选取参考文献[13],在保证对冲孔流通截面积不变的情况下,因素B选取圆形、椭圆形和矩形三个水平。对冲孔按照其长轴与消声器主轴线平行的方位布置,所以对冲孔的形状变化趋势是由圆形逐渐变为细长型的矩形。消声器对冲孔形状如图5所示。因素C根据内腔的长度和对冲孔的形状选取三个水平,分别为“Smin”、“Save” 和“Smax”。“Smin”表示两组对冲孔相距最近,两孔的近边之间相隔2 mm,“Smax”表示两组对冲孔相距最远,处于内腔两端的极限位置,“Save”表示“Smax”和“Smin”的平均值,对应结构如图6所示。

(a) 圆形对冲孔
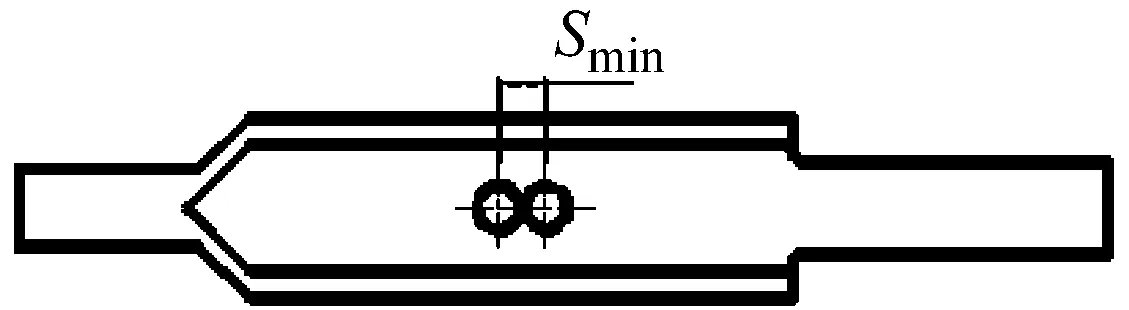
(a) 最小中心距
3.2.3 试验方案和结果
Box-Behnken响应面试验方案和结果如表2所示,共需要46组试验以完成试验因素及其交互作用对气流再生噪声总声压级的影响评判。
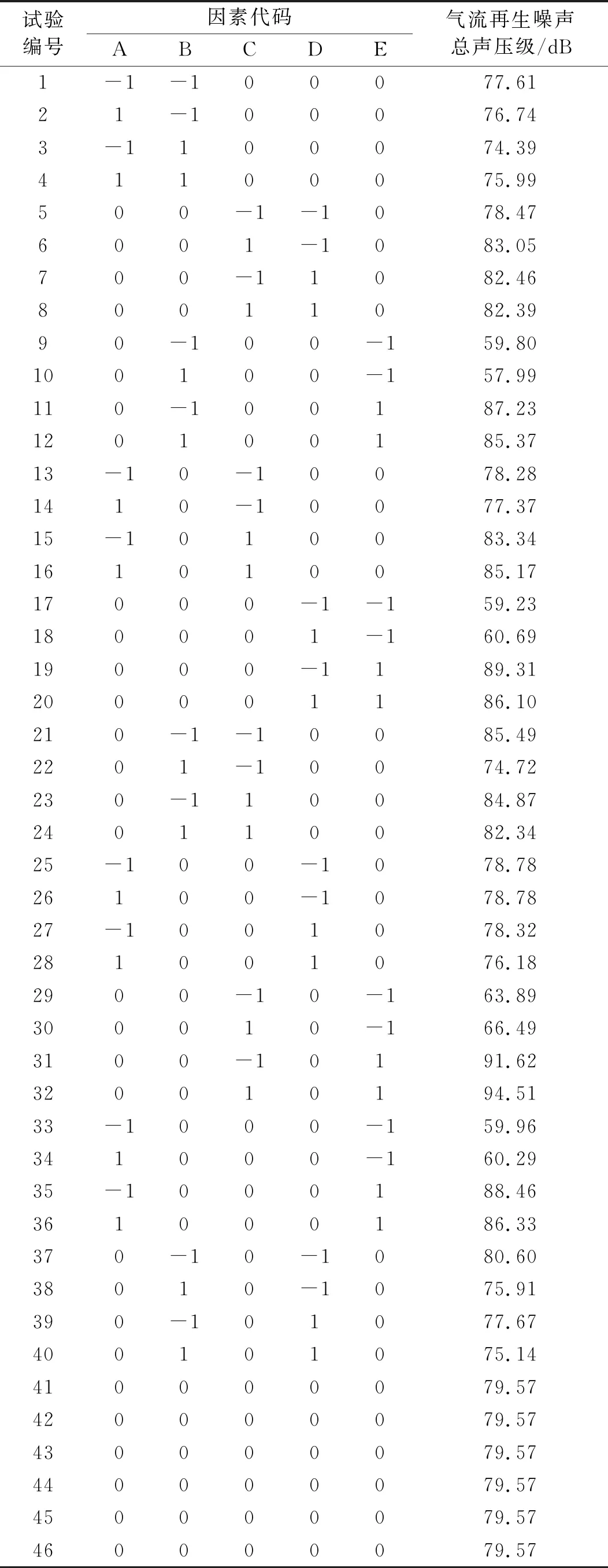
表2 试验方案及结果Tab.2 Experimental scheme and results
4 试验结果分析
4.1 回归分析与模型建立
Box-Behnken响应面试验结果分析包括回归分析和响应面分析。
4.1.1 响应模型选择
应用多种模型对试验数据进行建模,得到的模型分析结果如表3~5所示。
由表3的多种模型方差分析的结果来看,线性模型、2FI模型、二次方程模型和三次方程模型可以对气流再生噪声总声压级模型进行拟合,但2FI模型和三次方程模型的Prob>F大于0.05,说明该模型拟合不显著;从F值来看,线性模型和二次方程模型的拟合效果较优。表4为能够对气流再生噪声总声压级模型进行拟合的各种模型的R2综合分析,从比较结果来看,二次方程模型的R2大于0.9,而线性模型的R2小于0.9,且二次方程模型的R2校正值和R2预测值较为接近,说明二次方程模型与试验相关度较高,模型较准确且优于线性模型;综合表3和表4的分析结果,气流再生噪声总声压级响应模型选择二次方程模型。表5是对二次方程模型及模型中的各影响因素的置信度分析,表中各项估计参数为各项参数所在的95%置信区间的下值与上值的平均值。由各项估计参数绝对值的大小可推断各项对响应值的影响大小,结果为:E>C>B>D>A(一次项),BC>DE>CD>AC>AB>AE>BD>AD>CE>BE(不同因素交互作用项),E2>C2>B2>A2>D2(二次项),同时由各项的估计参数的正负值也可看出各项对响应值的效应方向,A、B、D、AD、AE、BE、CD、DE、A2、B2、D2、E2为负效应,其余均为正效应。
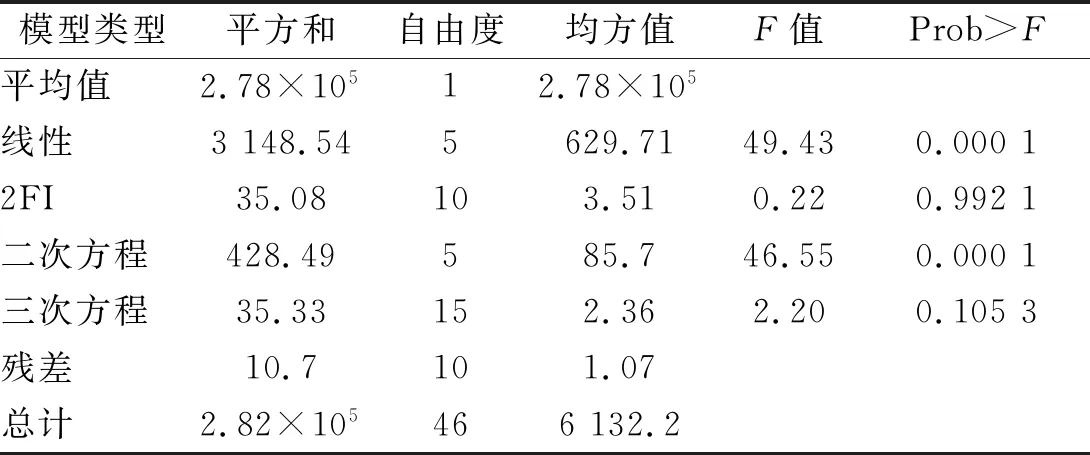
表3 多种模型方差分析Tab.3 Variance analysis of multiple fitting models
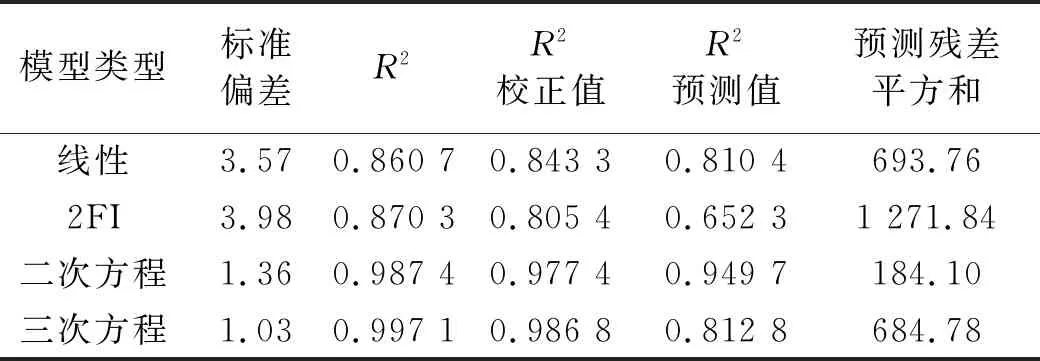
表4 R2综合分析Tab.4 R2 comprehensive analysis
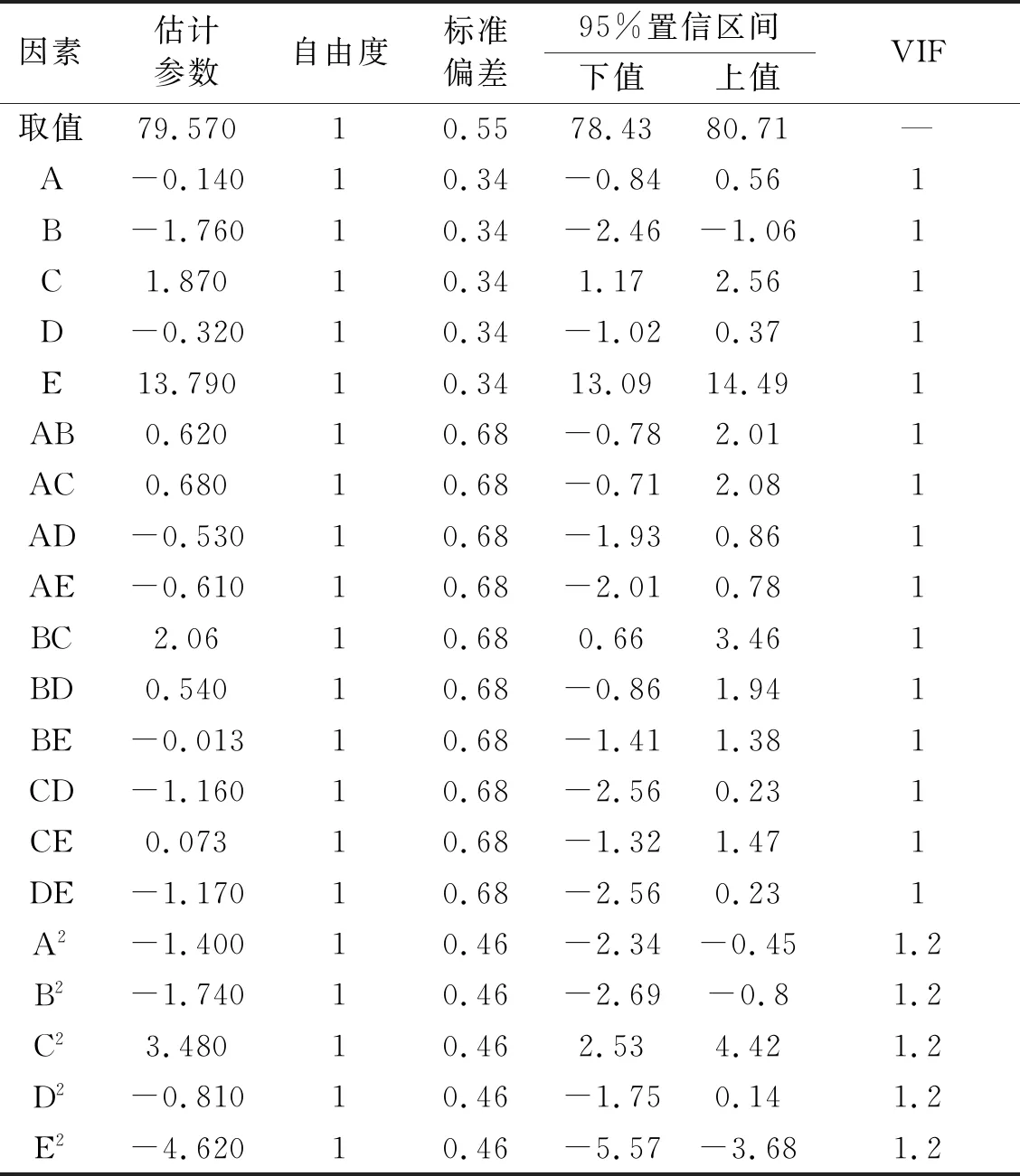
表5 模型方程参数估计Tab.5 Parameter estimation of model equation
最终由编码值表示的气流再生噪声总声压级数学模型为:Y=79.57-0.14A-1.76B+1.87C-0.32D+13.79E+ 0.62AB+0.69AC-0.54AD-0.62AE+2.06BC+0.54BD-0.01BE-1.16CD+0.07CE-1.17DE-1.40A2-1.74B2+3.48C2-0.81D2-4.62E2
4.1.2 模型验证
虽然在响应模型选择时已对各模型的符合程度做了比较,但比较F值、R2等都较为抽象,因此仍需以其它方式验证选定的模型。内在学生化残差用于绘制气流再生噪声总声压级的预测值与实际值对比(图7),图上点的分布近似为一条直线,说明模型预测可靠。
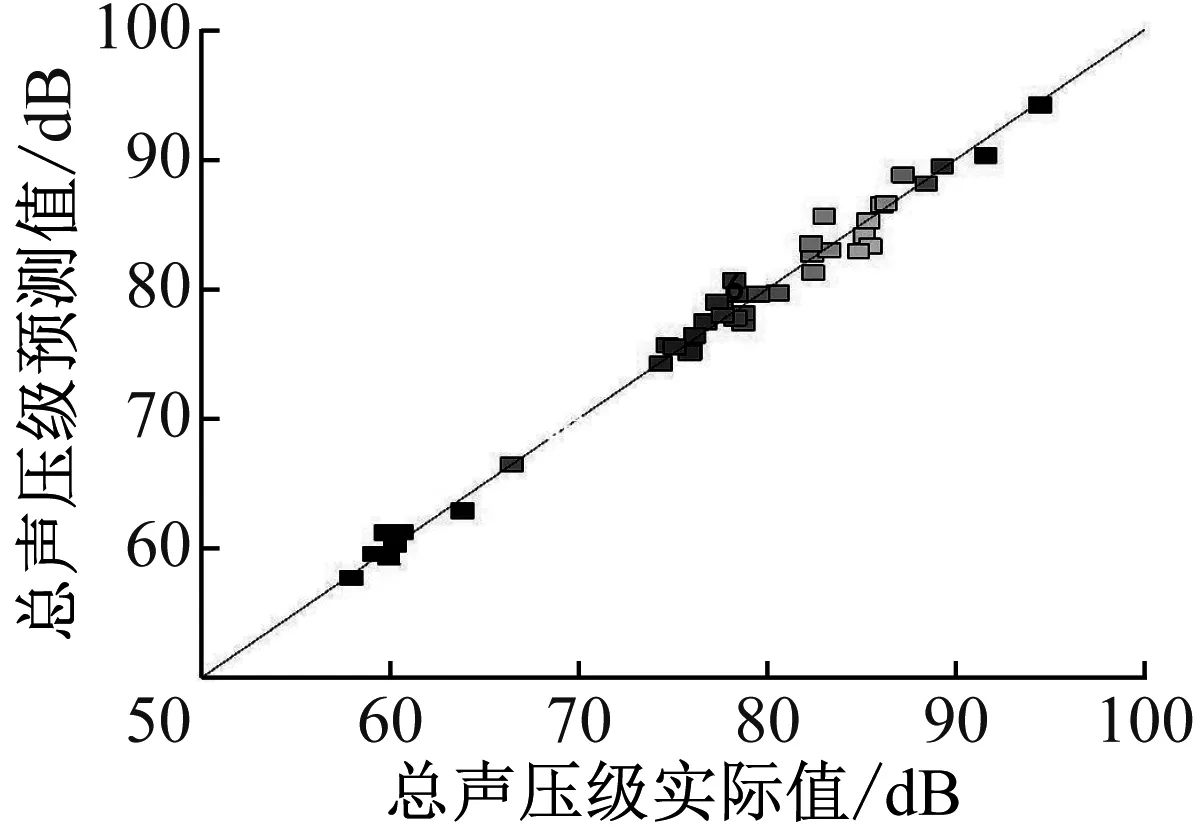
图7 总声压级预测值与实际值对比Fig.7 Comparison of predicted and actual total sound pressure level
4.2 气流再生噪声总声压级的影响因素分析
本文通过三维曲面图分析试验因素间二阶交互作用对气流再生噪声总声压级的影响,在图8中除分析的两种因素外,其余三种因素取值一定,均为Box-Behnken试验中各因素的0水平对应值,即内腔直径A=80 mm、对冲孔形状B=椭圆形、对冲孔中心距C=Save、内腔分流单元锥角D=60°、气流速度E=40 m/s。
图8(a)为内腔直径和对冲孔形状交互作用响应曲面。由图可见:内腔直径一定,对冲孔形状从圆形到矩形变化时,总声压级呈减小趋势;内腔直径为70 mm,对冲孔形状从圆形变化到矩形时,总声压级由78.95 dB减小为74.20 dB,减小了4.75 dB,减小趋势显著。当冲孔形状一定时,随着内腔直径的增大,总声压级先增大后减小,但整体呈增大趋势;对冲孔形状为矩形,内腔直径由70 mm增大到90 mm时,总声压级由74.20 dB增加为 75.15 dB,增大了0.95 dB,增大趋势不明显。
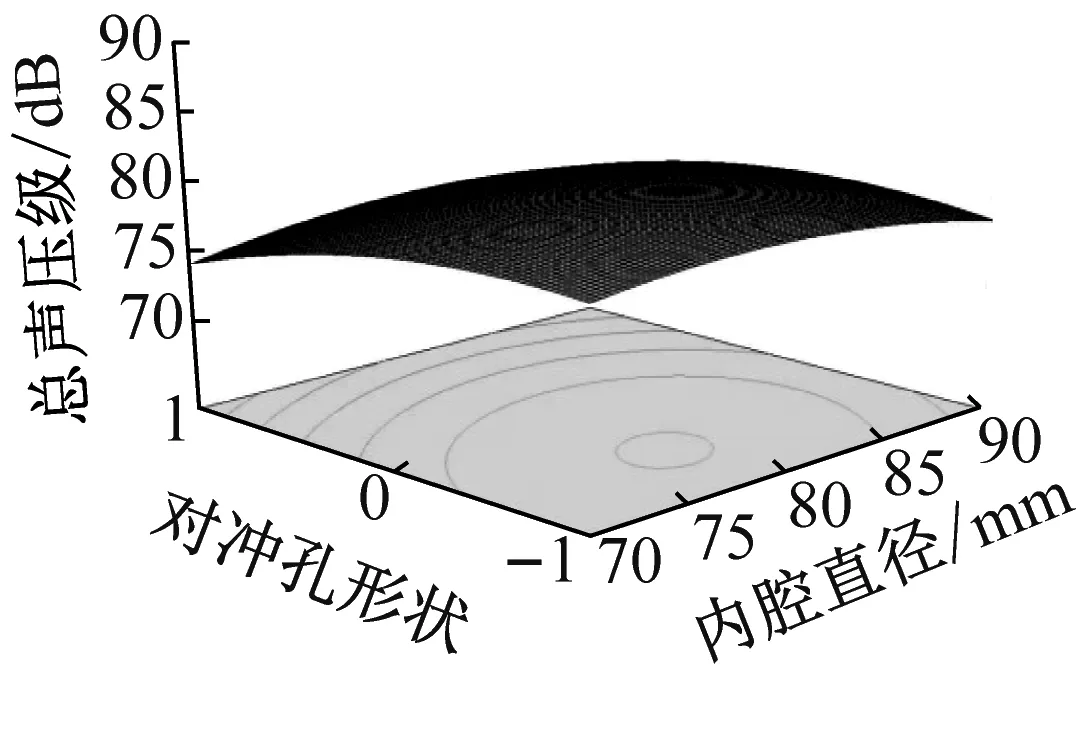
(a) 内腔直径和对冲孔形状交互作用响应面
图8(b)为内腔直径和对冲孔中心距交互作用响应曲面。由图可见:内腔直径一定,对冲孔中心距从Smin到Smax变化时,总声压级呈先减小后增大趋势;对冲孔中心距为Save时,总声压级最小。内腔直径为70 mm,对冲孔中心距从Smin变化到Smax时,总声压级由80.61 dB减小为78.32 dB后又增加为82.97 dB。当对冲孔中心距一定时,随着内腔直径的增大,总声压级先增大后减小;对冲孔中心距为Save,内腔直径由70 mm增大到90 mm时,总声压级由78.32 dB增加为 79.57 dB后又减小为78.03 dB。
图8(c)为内腔直径和内腔分流单元锥角交互作用响应曲面。由图可见:内腔直径一定,随着内腔分流单元锥角的变化,总声压级呈先增大后减小趋势,在内腔直径为70~75 mm时,总声压级增大部分的斜率大于减小部分的斜率,在内腔直径为75~90 mm时,总声压级增大部分的斜率小于减小部分的斜率。当内腔分流单元锥角一定时,内腔直径对总声压级的影响同图8(b)。
图8(d)为内腔直径和气流速度交互作用响应曲面。由图可见:随着气流速度的增加,总声压级显著增大;内腔直径为70 mm,气流速度从20 m/s增大到60 m/s时,总声压级由59.29 dB增加为 88.09 dB,增大了28.8 dB。当气流速度一定时,内腔直径对总声压级的影响同图8(b)。
图8(e)为对冲孔形状和对冲孔中心距交互作用响应曲面。由图可见:对冲孔形状一定,对冲孔中心距从Smin到Smax变化时,总声压级呈先减小后增大趋势;对冲孔中心距为Save时,总声压级最小。对冲孔形状为圆形,对冲孔中心距从Smin变化到Save时,总声压级由83.26 dB减小为79.59 dB,减小了3.67 dB,减小趋势较显著。对冲孔中心距介于Smin到Save,对冲孔形状从圆形到矩形变化时,总声压级呈减小趋势;对冲孔中心距为Smin,当对冲孔形状从圆形变化到矩形时,总声压级由83.26 dB减小为 75.62 dB,减小了7.64 dB,减小趋势显著。对冲孔中心距介于Save到Smax,对冲孔形状从圆形到矩形变化时,总声压级先增大后减小。
图8(f)为对冲孔形状和内腔分流单元锥角交互作用响应曲面。由图可见:内腔分流单元锥角一定,对冲孔形状从圆形到矩形变化时,总声压级呈减小趋势;内腔分流单元锥角为30°,当对冲孔形状从圆形变化到矩形时,总声压级由79.65 dB减小为75.05 dB,减小了4.6 dB,减小趋势显著。对冲孔形状一定,内腔分流单元锥角从30°到90°变化时,总声压级呈减小趋势;对冲孔形状为圆形,内腔分流单元锥角从30°变化到90°时,总声压级由79.65 dB减小为77.92 dB,减小了1.73 dB,减小趋势不显著。
图8(g)为对冲孔形状和气流速度交互作用响应曲面。由图可见:随着气流速度的增加,总声压级显著增大;对冲孔形状为圆形,气流速度从20 m/s增大到60 m/s时,总声压级由61.17 dB增加为88.76 dB,增大了27.59 dB,增大趋势极显著。气流速度一定时,对冲孔形状从圆形到矩形变化时,总声压级呈减小趋势;气流速度为40 m/s,对冲孔形状从圆形到矩形变化时,总声压级由79.59 dB减小为76.07 dB,减小了3.52 dB,减小趋势显著。
图8(h)为对冲孔中心距和内腔分流单元锥角交互作用响应曲面。由图可见:内腔分流单元锥角一定,随着对冲孔中心距从Smin到Smax变化时,总声压级呈先减小后增大趋势。对冲孔中心距介于Smin与Save之间,内腔分流单元锥角从30°~90°变化时,总声压级逐渐增大;对冲孔中心距为Smin,内腔分流单元锥角从30°变化到90°时,总声压级由79.53 dB增加为 81.21 dB,增大了1.68 dB。对冲孔中心距介于Save与Smax之间,内腔分流单元锥角从30°~90°变化时,总声压级逐渐减小;对冲孔中心距为Smax,内腔分流单元锥角从30°变化到90°时,总声压级由85.59 dB减小为 82.62 dB,减小了2.97 dB。
图8(i)为对冲孔中心距和气流速度交互作用响应曲面。由图可见:随着气流速度的增加,总声压级显著增大。气流速度一定,对冲孔中心距从Smin变化到Smax时,总声压级先减小后增大。
图8(j)为内腔分流单元锥角和气流速度交互作用响应曲面。由图可见:随着气流速度的增加,总声压级显著增大。气流速度一定,内腔分流单元锥角从30°~90°变化时,总声压级逐渐减小;气流速度为60 m/s,内腔分流单元锥角从30°变化到90°时,总声压级由89.42 dB减小为 86.44 dB,减小了2.98 dB。
4.3 试验方案优化及结果验证
在试验结果分析及回归模型的基础上,以气流再生噪声总声压级为优化指标,目标为最小值,当气流速度为40 m/s时,优化的前5个方案如表6所示。根据实际进行取整后得到最佳试验方案为:A=70 mm,B=矩形,C=Save,D=30°。当气流速度为20、40和60 m/s时,通过模型计算出的气流再生噪声总声压级分别为52.46 dB、72.62 dB和83.57 dB。
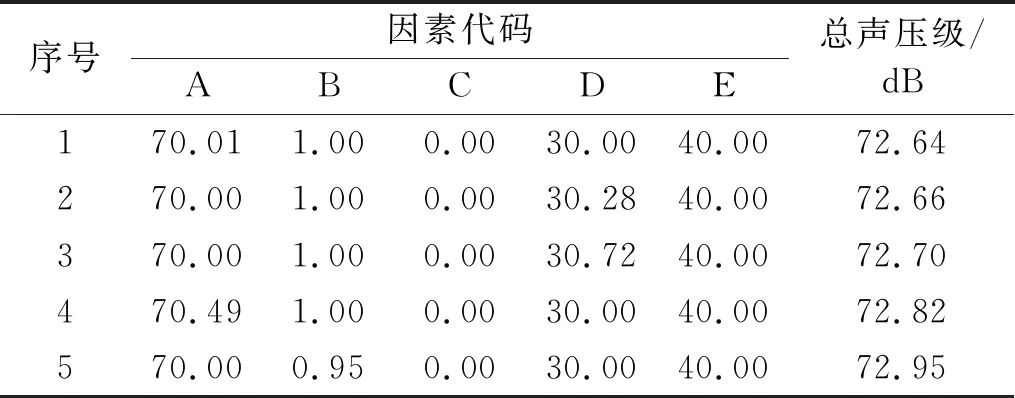
表6 气流再生噪声优化方案Tab.6 Optimization schemes of airflow regenerated noise
由于最佳试验方案未包含在Box-Behnken的46组试验中,需要进一步验证气流再生噪声总声压级数学模型的准确性。采用1.2.2节中的方法对优化后的方案进行建模和Fluent求解,得到气流速度为20、40和60 m/s时,最佳试验方案的气流再生噪声总声压级分别为55.08 dB、75.00 dB和85.72 dB。与气流再生噪声总声压级模型的计算值分别相差2.62 dB、2.38 dB和2.15 dB,相对误差分别为4.76%、3.17%和2.51%,相对误差较小,进一步表明气流再生噪声总声压级模型准确可靠,该模型可以对分流气体对冲排气消声器气流再生噪声进行预测。
5 结 论
(1) 采用Design-Expert软件对分流气体对冲排气消声器气流再生噪声试验进行设计和结果分析,经显著性检验和验证试验检验了所建数学模型的准确性,其相对误差范围小于5%,表明该模型可以对分流气体对冲排气消声器气流再生噪声进行预测。
(2) 通过模型方程参数估计分析了各单因素、不同因素二阶交互作用和因素二次项对响应值的显著程度:E(气流速度)>C(对冲孔中心距)>B(对冲孔形状)>D(内腔分流单元锥角)>A(内腔直径)(一次项),BC>DE>CD>AC>AB>AE>BD>AD>CE>BE(不同因素交互作用项),E2>C2>B2>A2>D2(二次项)。表明气流速度、对冲孔中心距和对冲孔形状是分流气体对冲排气消声器气流再生噪声的主要影响因素。
(3) 通过三维曲面图分析了试验因素间二阶交互作用对响应值的影响规律。结果表明:随着气流速度的增大,气流再生噪声总声压级显著增大,斜率都超过了1,表明气流速度是气流再生噪声产生的主要因素;对冲孔形状和对冲孔中心距对气流再生噪声影响较显著,且当冲孔形状为矩形、对冲孔中心距为Save时,气流再生噪声总声压级较小;内腔分流单元锥角和内腔直径对气流再生噪声的影响较小。
(4) 以气流再生噪声总声压级为优化指标,得到了最佳试验条件为:内腔直径为70 mm,对冲孔形状为矩形,对冲孔中心距为92.8 mm,内腔分流单元锥角为30°时,气流再生噪声最小。
