微尺度CSP焊点弯振耦合应力应变分析与优化

2021-05-17黄春跃付玉祥

振动与冲击 2021年9期

高超，黄春跃，梁颖，付玉祥，匡兵

(1.桂林电子科技大学机电工程学院，桂林 541004；2.成都航空职业技术学院信息工程学院，成都 610021)

随着手机、数码相机、移动存储设备和智能可穿戴设备等消费类电子产品小型化、多功能化、高集成度化及低成本需求日益增长，由此一方面使得方形扁平无引脚封装(quad flat no-lead package，QFN)、球栅阵列封装(ball grid array，BGA)和芯片尺寸封装[1]等各种面阵列型器件广泛应用于这些电子产品中，以在保证产品性能的前提下提高产品中电路模块的组装密度而减小产品体积和重量；但在这类面阵列型器件中起着信号传递和机械支撑重要作用的互连焊点的焊点间距、焊点高度以及焊点直径都非常小(乃至小至微尺度)，因此大大降低了其连接刚度；而另一方面，电子产品的电路模块在再流焊焊接过程、组装过程及使用过程中均会产生不同程度的弯曲变形，因弯曲变形均会造成电子产品中的面阵型器件的焊点产生裂缝、刚度变化和变形等损伤，进而降低电子产品使用寿命；与此同时，电子产品不可避免的会在机载、车载和船载等环境中使用，在这些环境中电子产品内的面阵型器件焊点由此会承担着随机振动载荷作用。因此，电子产品的实际复杂使用环境决定了电子产品中的面阵型器件焊点不可避免的会同时处于弯曲载荷和振动载荷共同作用，由此带来了更为严峻的可靠性挑战。

对于面阵型器件焊点在弯曲加载条件下可靠性问题，国内外学者已经展开了相关研究工作，如殷芮等[2]分析了焊点材料、焊点间距、印制电路板(printed circuit board,PCB)支撑跨度及焊点阵列对微尺度BGA焊点弯曲应力应变的影响；王玲等[3]对BGA焊点进行了温度循环及弯曲可靠性能试验研究；Chang等[4]研究了循环弯曲加载对BGA焊点性能的影响；Lau等[5]对BGA焊点进行了三点弯曲试验测试，验证了三点弯曲作用下BGA焊点阵列的最大应力应变出现在阵列的边角处。针对面阵型器件焊点随机振动可靠性问题，韦何耕等[6]引入模糊理论修正钎料的应力-寿命曲线(S-N curve)，并结合三带技术对叠层 PBGA 焊点随机振动疲劳寿命进行了计算；王红芳等[7]研究了振动环境对倒装焊点可靠性的影响；Kim等[8]通过仿真分析和试验验证相结合对BGA焊点进行了随机振动载荷下和热循环载荷下的可靠性分析研究；Chen等[9]与Che等[10]分别对BGA焊点进行了正弦振动可靠性试验，并利用线性累积损伤方法来研究焊点振动疲劳寿命；Liu等[11]研究了不同应变水平和振动频率下BGA封装焊点的振动可靠性并进行了寿命预测；黄春跃等[12]对CSP焊点进行了热结构耦合分析和温振耦合分析，获得了微尺度 CSP 焊点应力应变分布结果；刘芳等[13]采用基础激励法对电路板组件进行了随机功率谱分析。以上国内外学者的研究工作一方面表明了对面阵列型器件焊点开展弯曲和振动加载条件下可靠性研究有其必要性，另一方面也表明已有研究工作中尚有不足，如已有研究大多是在单独弯曲加载或者单独随机振动加载条件下对面阵列型器件焊点进行可靠性研究，而未能对面阵列型器件焊点在弯振复合加载条件下的可靠性开展相关研究，对此，本文以面阵列型器件中的CSP器件微尺度焊点为研究对象，对其在弯振复合加载条件下的应力应变进行分析，分析微尺度CSP焊点材料和焊点结构参数对弯振耦合应力应变分布规律的影响，在此基础上采用响应面法与粒子群算法相结合的方法进行以微尺度CSP焊点弯振耦合应力最小为目标的优化设计，得到最优的焊点结构参数水平组合，以降低焊点内最大弯振耦合应力，从而实现微尺度CSP焊点抗弯振性能的提高。

1 微尺度CSP焊点弯振耦合条件下有限元分析

1.1 微尺度CSP焊点三维有限元模型

本文采用有限元分析法对微尺度CSP焊点在弯振复合加载条件下的应力应变进行分析研究。图1所示为采用ANSYS软件建立的三维微尺度CSP焊点弯振耦合应力应变有限元仿真分析模型。为确保微尺度CSP焊点模型形态的准确性，通过基于最小能量原理的Surface Evolver软件来获取CSP焊点的外形尺寸参数。

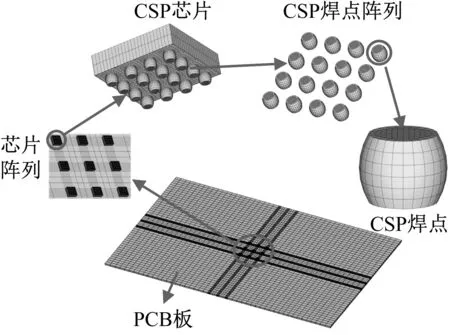
图1 微尺度 CSP 焊点弯振耦合应力应变有限元分析模Fig.1 Coupling stress-strain finite element analysis model of microscale CSP solder joints

为了便于问题分析，在某种程度上简化了模型，即不考虑焊点与PCB板之间的铜焊盘，并假定焊点无空穴和气孔等缺陷[14]。有限元模型由CSP芯片、微尺度CSP焊点和PCB板三部分组成，其中CSP芯片共9块(3×3布局)，9块芯片下的微尺度CSP焊点(以下简称为CSP焊点)阵列均为4×4全阵列焊点，CSP芯片及其焊点参数来源于美国Fairchild公司生产的型号为FAN48632UC33X的CSP芯片，芯片尺寸均为1.63 mm×1.63 mm×0.4 mm，焊点总数为144个，焊点高度为0.18 mm、焊点直径为0.23 mm、焊盘直径为0.18 mm、焊点间距为0.4 mm、芯片间距为5 mm，CSP焊点材料为无铅焊料SAC305。模型中PCB尺寸为132 mm×77 mm×1 mm。进行有限元网格划分时CSP焊点单元类型选择为Solid185，模型中其他部分的单元类型选择为Solid45。为减小网格变化对CSP焊点应力应变的影响，采用映射网格划分方式对三维有限元模型进行网格划分，并且对CSP焊点与芯片和PCB板接触部分进行网格细化以得到更精确的有限元分析结果，整个模型网格划分后单元数为181 504个。模型中各部分材料参数以及不同焊点材料参数如表1所示。

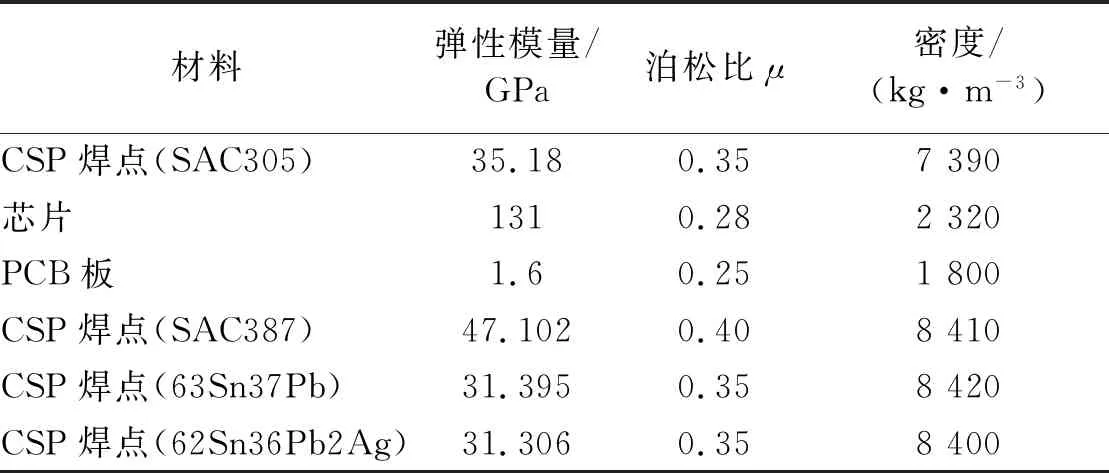
表1 材料参数Tab.1 Material properties

1.2 CSP焊点弯振耦合应力应变分析流程及加载条件

弯振耦合应力应变分析是指CSP焊点模型在进行有限元仿真分析时考虑了应力和振动两个物理场的交叉影响作用。本文对CSP焊点弯振耦合应力应变分析时采用了间接耦合的分析方法，主要分为两个阶段完成：① 结构场分析，对CSP焊点在弯曲加载条件下的应力应变进行分析；② 将结构场分析得到的结果作为预应力加载到CSP焊点有限元模型上，再进行随机振动分析，得到弯振耦合应力应变分析结果。

① 弯曲装置;② 测试样件;③ 测量界面;④ 计算器;⑤ 动态应变测量仪;⑥ 振动激励模块图9 应变测量系统Fig.9 Strain measurement system

图2所示为进行第一阶段弯曲应力应变分析时对CSP焊点进行弯曲加载的示意图。如图2所示，带有CSP焊点的芯片以朝下方式置于PCB板中间部位，将PCB固定约束在离中心相等距离的支撑刚体上，然后在两个支撑架中点处(PCB的另一侧)向下施加位移载荷，在位移载荷作用下CSP焊点即可产生弯曲应力应变。分析时所施加的位移载荷大小为2.0 mm，模型的支撑跨度(跨距)为100 mm；约束条件是两个支撑处上的所有节点施加全约束。

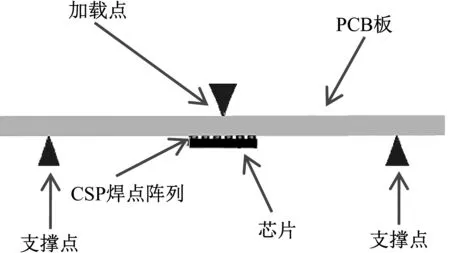
图2 微尺度CSP焊点弯曲加载示意图Fig.2 Micro-scale CSP solder joint bending loading diagram

图3所示为进行第二阶段随机振动应力应变分析时所采用的PSD(power spectral density,PSD)加速度功率谱加载条件，来源于美国军标MIL-STD NAVMAT P9492，即随机振动频率在20～80 Hz时，PSD曲线上升斜率为+3 dB/oct，对应的加速度功率谱密度幅值范围为0.01～0.04 g2/Hz，80 Hz时为0.04 g2/Hz；当随机振动频率在80～350 Hz时，对应的加速度功率谱密度幅值为0.04 g2/Hz，当随机振动频率在350～2 000 Hz时，PSD曲线以-3 dB/cot的斜率下降，对应的加速度功率谱密度幅值范围为0.04～0.01 g2/Hz。

图3 随机振动和速功率谱加密度曲线Fig.3 Random vibration PSD curve

1.3 CSP焊点弯振耦合应力应变分析结果

在ANSYS软件中对CSP焊点三维有限元模型进行弯曲振动耦合分析所得最终结果如图4和图5所示。图4和图5分别为CSP焊点内的弯振耦合范米塞斯(Von Mises)等效应力和等效应变(以下简称应力应变)云图。

图4 微尺度CSP焊点内弯振耦合应力分布云图Fig.4 The bending vibration coupling stress distributions contours of micro-scale CSP solder joints

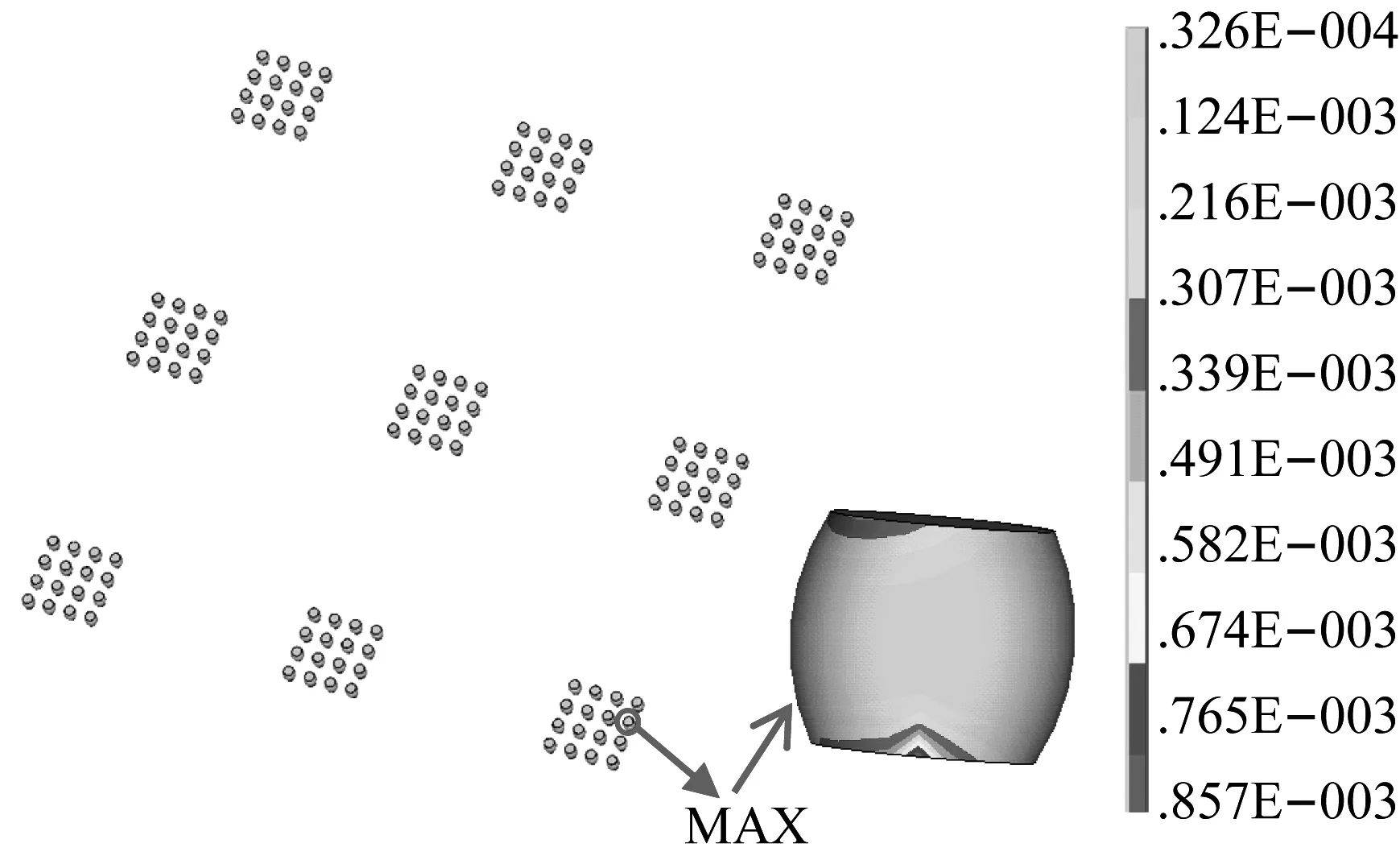
图5 微尺度CSP焊点内弯振耦合应变分布云图Fig.5 The bending vibration coupling strain distributions contours of micro-scale CSP solder joints

由图4和图5可见，当PCB板在弯振复合加载条件下产生变形时，CSP焊点内相应产生弯振应力应变，在3×3布局的不同芯片下的CSP焊点内的应力应变大小均不同，相比较而言，其中位于3×3布局中间一列芯片下的CSP焊点应力应变较小，而另外两列芯片下的CSP焊点应力应变较大；对于同一芯片下的CSP焊点阵列，位于阵列内中间的两列焊点的应力应变较小，而位于阵列内最外层的两列焊点的应力应变较大；对于单个CSP焊点，焊点内的应力应变由焊点中间向两侧逐渐增大，最大应力应变出现在距中心位置最远端的芯片下，且位于该芯片下焊点阵列最外层焊点与PCB板接触面处，最大弯振耦合应力和最大弯振耦合应变分别为30.2 MPa和0.000 857。从CSP焊点最大弯振耦合应力应变出现位置可知，在弯振耦合加载条件下，在CSP焊点与PCB板接触面处会最先产生由弯振耦合应力应变所致的微裂纹，在持续的弯振耦合载荷作用下微裂纹扩展到整个接触面后导致CSP焊点互连失效，从而造成互连可靠性问题。

1.4 CSP焊点纯弯曲与弯振耦合加载应力应变对比分析

采用与图1所示的相同的分析模型并只施加相同的2.0 mm弯曲位移载荷，对CSP焊点进行纯弯曲加载条件下的应力应变分析，所得CSP焊点弯曲应力应变分布情况分别如图6和图7所示。

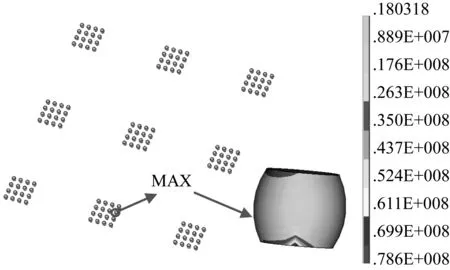
图6 微尺度 CSP 焊点内弯曲应力分布云图Fig.6 The bending stress distributions contours of micro-scale solder joints

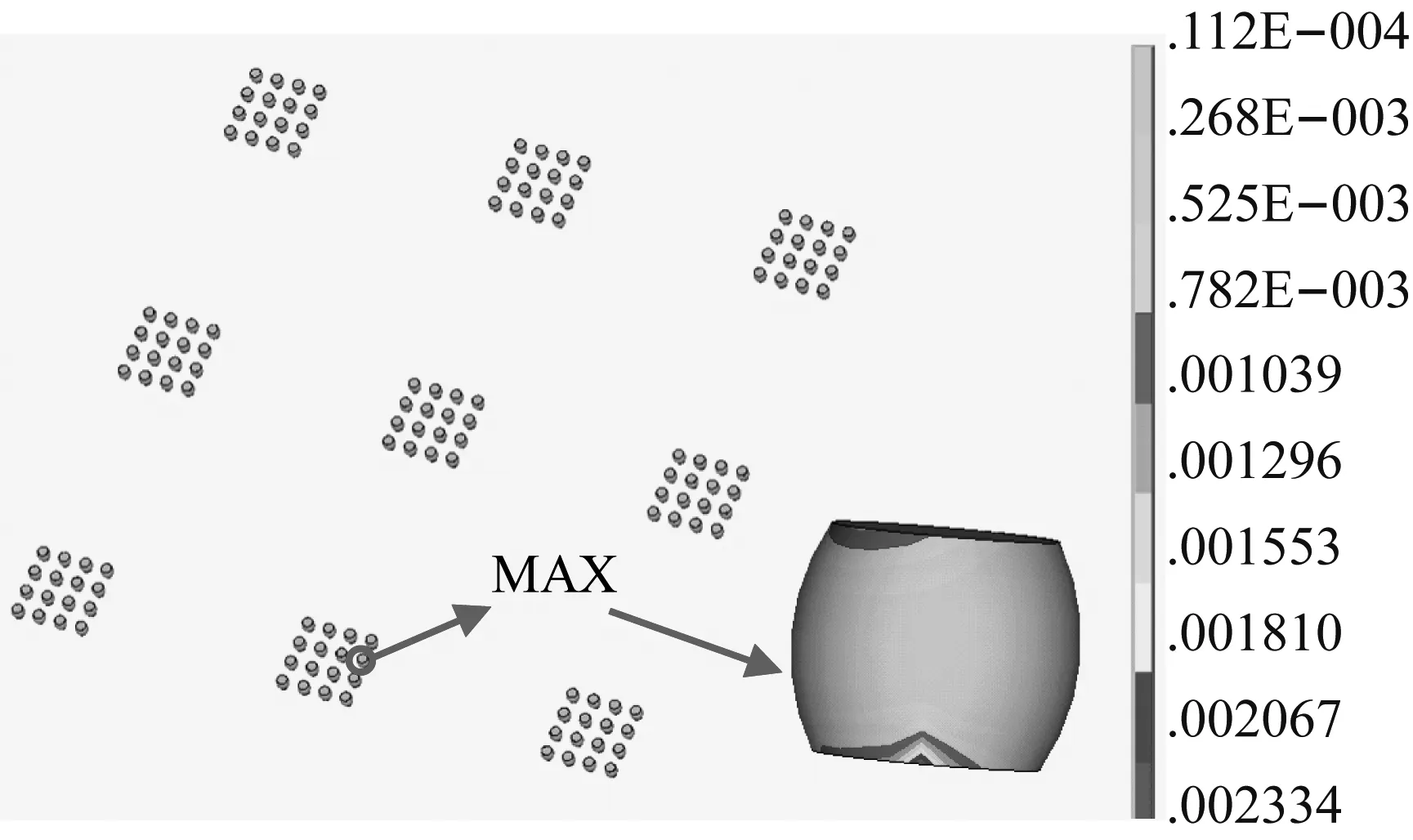
图7 微尺度 CSP 焊点内弯曲应变分布云图Fig.7 The bending strain distributions contours of micro-scale solder joints

由图6和图7可见，当PCB板在纯弯曲加载条件下产生变形时，CSP焊点内产生弯曲应力应变，不同焊点内的弯曲应力应变均不相同，位于3×3布局的芯片阵列中间一列芯片下的焊点应力应变最大，另外两列芯片下的焊点应力应变最小，与弯振复合加载条件下CSP焊点应力应变结果不同；同一芯片下的焊点阵列内中间两列焊点的应力应变较小，最外层两列焊点应力应变较大；对单个焊点，其内部的弯曲应力应变从中间向两侧逐渐增大，这与弯振复合加载条件下CSP焊点应力应变分布情况相同；最大弯曲应力应变出现在中心位置芯片下焊点阵列内的最外层焊点上，且最大弯曲应力应变出现在与PCB板接触的一端，最大弯曲应力和最大弯曲应变分别为78.6 MPa和0.002 324，均大于1.3节所述相同条件下的弯振耦合应力应变。

2 CSP焊点弯振耦合应变与纯弯曲应变试验验证

本文设计并完成了CSP焊点弯振耦合应变测量与纯弯曲应变测量的试验以验证仿真分析结果的准确性。测量应变通常利用应变片来完成，因此本文制作了与图1所示仿真模型相同的应变测试试验样件，并利用应变片花完成对试验样件弯振耦应变和纯弯曲应变的测量。制作好的试验样件如图8所示，包括9块CSP芯片(3×3布局、型号FAN48632UC33X)。在测试点上粘贴应变片后完成对测试点上弯振耦合应变和纯弯曲应变的测量。通过比较测试点处试验测量得到的应变和仿真模型上相同位置处通过仿真分析所得的应变的相符合程度，即可验证仿真方法所得结果是否准确。本文1.1节所述的仿真模型在建立时参考了JESD22B113标准中的相关规定，因此在进行试验样件的弯振耦合应变与纯弯曲应变测量时，应变片的放置位置也参考了该标准中对应变片在试验样件上的布置规定。

图8 试验样件Fig.8 Test sample

为了实现应变测量，设计制作了如图9所示的应变测量平台。该测量平台主要包括：测试样件(含直角应变花)、弯曲装置、振动激励模块、动态应变测量仪和计算机等。该测量平台通过弯曲装置对测试样件施加弯曲位移载荷，与此同时由振动激励模块带动整个试验样件产生振动从而实现弯振耦合加载，再通过动态电阻应变仪记录下弯振耦合加载过程测试样件相应测试点处的应变值。在获取了测试样件测试点处的应变值后，通过直角应变花主应变计算公式(1)即可以计算得到相对应的测试点处的弯振耦合应变。在纯弯曲加载测量时，不开启振动激励模块即可测量获取纯弯曲加载条件下的应变。

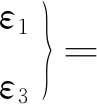
(1)

式中：ε1和ε3为主应变；ε0°、ε45°和ε90°分别为直角应变花0°、45°和90°三个方向上应变片所测量到的应变。

首先进行纯弯曲加载测量，通过弯曲装置在测试样件上施加2.0 mm弯曲位移载荷对测试点处的应变进行测量。测量得到测试点处三个方向上的应变ε0°、ε45°和ε90°分别为5.067×10-4、1.054×10-3和1.762×10-4，通过式(1)可计算出测试点处的第一和第三主应变数据如表2所示。根据试验测试样件上测试点处应变片测量的区域，在图1所示的仿真模型中选取相同区域的节点，得到相同区域节点处的第一和第三主应变仿真值也列出在表2中。对比试验测量结果与仿真结果可知，试验与仿真第一、第三主应变的结果误差分别为4.155%和6.546%；仿真结果和试验测量误差均小于10%，试验测试结果验证了纯弯曲加载仿真分析结果的准确性，故采用仿真方法对CSP焊点进行纯弯曲加载分析是有效的。

表2 纯弯曲应变试验测量数据Tab.2 Experimental measurement data of bending strain

其次进行弯振耦合加载测量，通过弯曲装置与振动激励模块，在测试样件上施加2.0 mm弯曲位移载荷的同时通过振动激励模块施加振动载荷，对测试点处的应变进行测量。测量得到测试点处三个方向上的应变ε0°、ε45°和ε90°分别为2.046×10-4、5.594×10-4和1.094×10-4，通过式(1)可计算出测试点处的第一和第三主应变数据如表3所示。根据试验测试样件上测试点处应变片测量的区域，在图1所示的仿真模型中选取相同区域的节点，得到相同区域节点处的第一和第三主应变仿真值也列出在表3中。对比表3所示试验测量结果与仿真结果可知，第一和第三主应变的试验值与仿真值结果误差分别为5.754%和7.326%；仿真结果和试验测量误差均小于10%，试验测试结果验证了弯振耦合加载仿真分析结果的准确性，故采用仿真方法对CSP焊点进行弯振耦合加载分析是有效的。

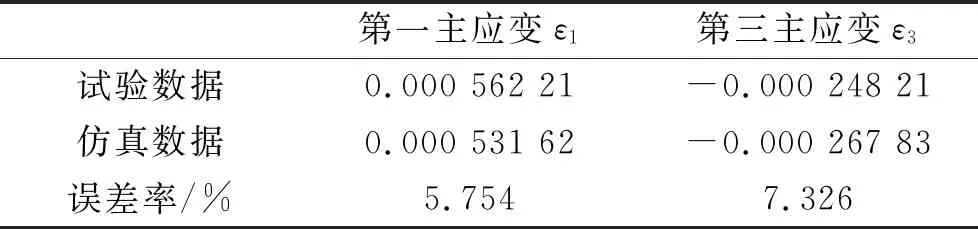
表3 弯振耦合应变试验测量数据Tab.3 Experimental measurement data of bending vibration coupling strain

此外，对比表2所示纯弯曲应变试验测量数据和表3所示弯振耦合应变试验测量数据还可以发现弯振耦合加载的第一和第三主应变值在数值上均小于纯弯曲加载测的第一和第三主应变值，这也验证了文中1.4节仿真分析中纯弯曲仿真结果大于弯振耦合仿真结果的准确性。

3 CSP 焊点材料以及焊点结构参数对弯振耦合应力应变影响分析

3.1 焊点材料对焊点弯振耦合应力应变影响分析

根据1.1节中所建立的CSP焊点弯振耦合应力应变有限元分析模型，在只改变焊点材料而其他参数不变的情况下，建立SAC305、SAC387、63Sn37Pb和63Sn36Pb2Ag这四种不同焊点材料的有限元模型并进行弯振耦合加载分析，获得不同焊点材料的CSP焊点最大弯振耦合应力应变结果如图10和表4所示。

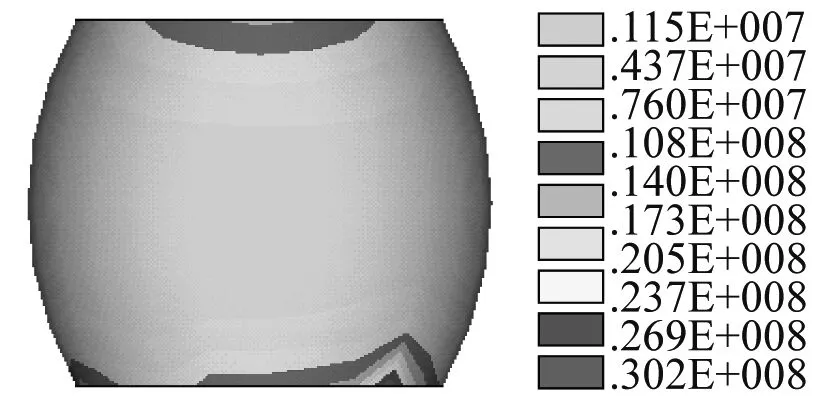
(a) SAC305

表4 不同焊点材料的微尺度焊点弯振应力应变Tab.4 Bending vibration coupling stress and strain of micro-scale solder joints with different solder joint material

由图10可知，当只有焊点材料发生改变，其他焊点结构参数均不变时，CSP焊点弯振耦合应力应变均发生相应的改变，焊点与PCB板接触面处的弯振耦合应力应变大于焊点与芯片接触面处的弯振耦合应力应变；由表4可知，采用焊点材料SAC387的CSP焊点内的最大弯振应力耦合最大，为35.2 MPa；采用焊点材料62SnPb2Ag的CSP焊点内的最大弯振耦合应力最小，为28.2 MPa；采用材料62Sn36Pb2Ag的CSP焊点内的最大弯振耦合应变最大，为0.000 901；采用焊点材料SAC387的CSP焊点内的最大弯振耦合应变最小，为0.000 749。

3.2 焊点结构参数对焊点弯振耦合应力应变影响分析

本小节对焊点结构参数进行单因素分析，以获得焊点直径、焊点高度和焊盘直径的变化对焊点弯振耦合应力的影响规律。在只改变焊点直径而其他参数不变的情况下，建立0.21 mm、0.23 mm、0.25 mm和0.27 mm这四种不同焊点直径的有限元模型进行弯振耦合加载应力应变分析，获得不同焊点直径的CSP焊点弯振耦合应力应变，结果如表5所示；在只改变焊点高度而其他参数不变的情况下，建立0.14 mm、0.16 mm、0.18 mm和0.20 mm这四种不同焊点高度的有限元模型进行弯振耦合加载应力应变分析，获得不同焊点高度的CSP焊点最大弯振耦合应力应变，结果如表6所示；在只改变焊盘直径而其他参数不变的情况下，建立0.14 mm、0.16 mm、0.18 mm和0.20 mm这四种不同焊盘直径的有限元模型进行弯振耦合加载应力应变分析，获得不同焊盘直径的CSP焊点最大弯振耦合应力应变，结果如表7所示。(限于篇幅仅以表格形式给出应力应变数据)。

表5 不同焊点直径的焊点弯振应力应变Tab.5 Bending vibration coupling stress and strain of micro-scale solder joints with different diameters

表6 不同焊点高度的焊点弯振应力应变Tab.6 Bending vibration coupling stress and strain of micro-scale solder joints with different solder joint heights

表7 不同焊盘直径的焊点弯振应力应变Tab.7 Bending vibration coupling stress and strain of micro-scale solder joints with different pad diameters

由表5可知，不同焊点直径的CSP焊点最大弯振耦合应力各不相同，CSP焊点的最大弯振耦合应力应变随着焊点直径的增大而增大；由表6可知，不同焊点高度的CSP焊点最大弯振耦合应力各不相同，CSP焊点的最大弯振耦合应力应变随着焊点高度的增大而减小；由表7可知，不同焊盘直径的CSP焊点最大弯振耦合应力各不相同，CSP焊点的最大弯振耦合应力应变随着焊盘直径的增大而减小。

4 基于响应面-粒子群算法的CSP焊点结构参数优化

由第3章分析可知，CSP焊点结构参数的变化会对焊点弯振耦合应力应变产生影响，为了降低CSP焊点在弯振复合加载条件下的应力应变以提高其在弯振加载环境中的可靠性，对其结构参数进行优化设计以获得应力应变最低的最优的焊点结构参数组合是及其必要的。对此，本文利用响应面法与粒子群算法相结合的优化方法，针对包括焊点直径、焊点高度和焊盘直径在内的焊点结构参数，以CSP焊点弯振耦合应力最小为优化目标，获得CSP焊点最优结构参数水平组合。

4.1 基于响应面法的仿真试验设计

本文采用响应面法建立CSP焊点弯振耦合应力与焊点结构参数的关系式。选取CSP焊点的3个结构参数焊点直径L、焊点高度H和焊盘直径D，且这3个参数均分别取3个水平值，其因素的水平表如表8所示。

表8 因素水平表Tab.8 The table of levels and factors

选用Box-Behnken试验设计方法获得焊点因素水平组合，如表9所示。表9中共有17组CSP焊点结构参数水平组合，其中12组为分析因子，其余5组用于试验误差估计的零点因子，其参数水平组合完全相同。以这17组CSP焊点结构参数水平组合分别建立17组仿真分析模型进行弯振耦合加载仿真分析，得到相应的各组焊点的弯振耦合最大应力值如表9最后一列所示。

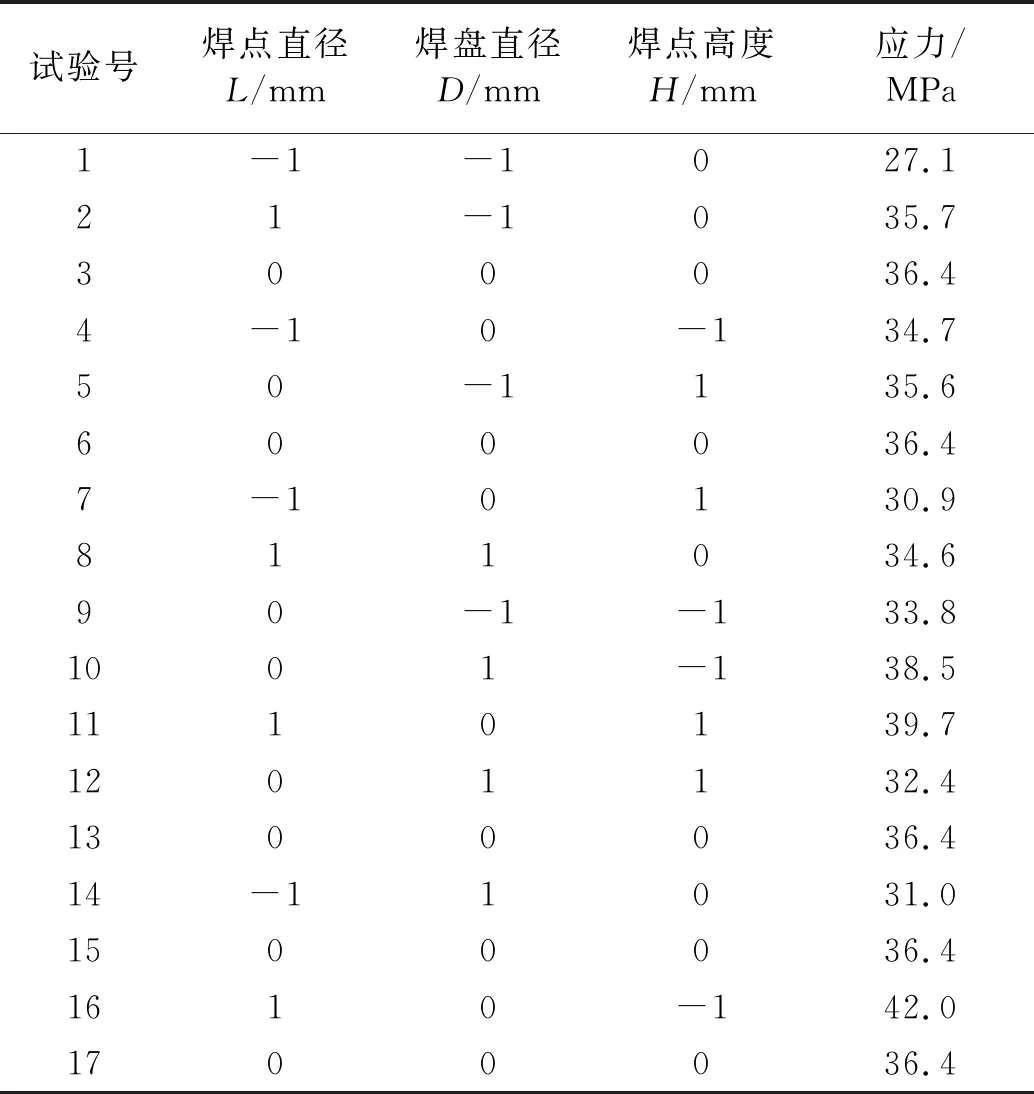
表9 响应曲面组合与应力分析结果Tab.9 Response Surface combination and stress analysis results

4.2 响应曲面分析

响应曲面分析可选用的数学模型比较多，其中包括一元线性回归模型、多元线性回归模型和多项式回归模型等。根据微积分知识，任一函数都可由若干个多项式分段近似表示，因此在实际问题中，无论变量和结果间关系复杂程度如何，总可以用多项式回归来分析计算，由于本文设计变量为3个且变量与目标之间函数关系为非线性，结合表9的试验样本数，选用基于泰勒展开式的二阶多项式模型如式(2)所示

(2)

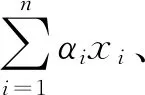
Y=36.40+3.54×X1+0.54×X2-1.30×X3-

1.25×X1×X2+0.38X1×X3-1.98×X2×X3

(3)

为了确保回归方程可信，对上式进行了方差分析和模型的显著性验证，得到回归方程相关联评价指标，结果如表10所示。

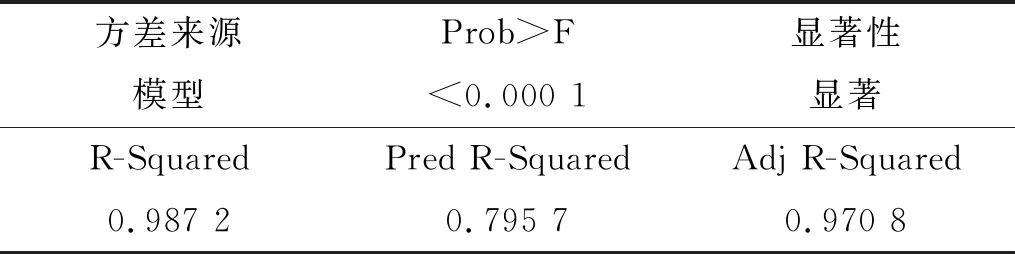
表10 响应面分析结果Tab.10 Response surface analysis

由表10中数据可知，响应曲面分析得到的模型“Prob>F”小于0.000 1(一般小于0.05即表示该项显著)，即响应曲面模型回归效果特别明显；回归方程系数R-Squared为0.987 2，表明回归方程拟合度很高；回归方程调整系数Adj R-Squared为0.970 8，更准确的反映出方程的拟合度很高；回归方程预测系数Pred R-Squared为0.795 7，表明方程预测准确度良好。以上结果系数都表明式(3)能够高度拟合表9中的试验结果，故回归方程准确可信。

4.3 CSP焊点结构参数优化

本文基于粒子群算法在MATALAB上实现算法编程，对回归方程式(3)实现最优解的搜索，以达到优化焊点结构参数的目的。根据表9设置了约束条件，分别将焊点直经(X1)、焊盘直径(X2)和焊点高度(X3)进行约束，0.18≤X1≤0.22、0.13≤X2≤0.15、0.14≤X3≤0.16，粒子的数量为1 000，最大迭代次数为1 500次,学习参数都设置为1.496 2，惯性权重为0.6，粒子各维最大速度Vmax限制为0.1倍该维自变量的上限，各维最小速度Vmin限制为软件的计算精度[15]，迭代后目标函数值如图11所示。

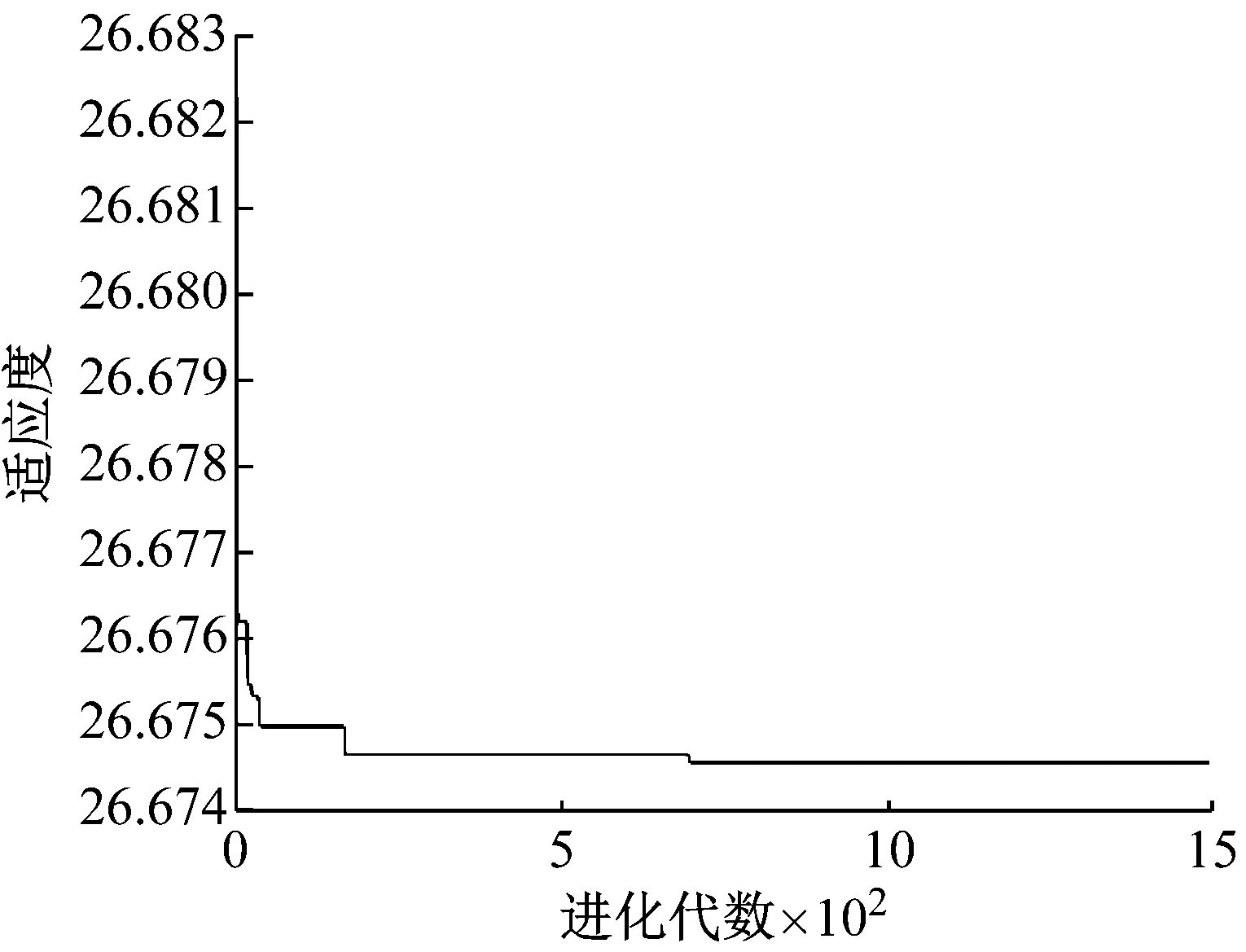
图11 迭代过程种群目标函数均值变化和最优解变化Fig.11 Mean change and optimal solution of population objective function during the iterative process

图11为回归方程(3)基于PSO的寻优历程，目标函数经过1 500次迭代进化，全局最优解为26.674 MPa，输出各个结构参数的最优水平值为：X1=0.18 mm，X2=0.15 mm，X3=0.16 mm，目标函数的最优解26.674 MPa，该最优解与表9中所示的最小应力27.1 MPa相比减小了0.7 MPa，达到了CSP焊点结构参数优化的目的。

4.4 最优结构参数水平组合验证

基于响应面法-粒子群算法得到了CSP焊点结构参数最优水平组合，即焊点直径为0.18 mm、焊点高度为0.16 mm和焊盘直径为0.15 mm，为了验证该最优水平组合的有效性，在设定其他条件不变的情况下，根据上述CSP焊点结构参数水平组合建立相应的有限元分析模型进行弯振耦合加载分析，所得结果如图12所示。根据图13的仿真结果可知，在弯振复合加载条件下CSP焊点最大应力值为24.8 MPa，与表9中所示的所有水平组合的CSP焊点的最大弯振耦合应力中最小的27.1 MPa相比减小了2.3 MPa，由此验证了采用响应面法-粒子群算法所得到的CSP焊点最优结构参数水平组合使焊点内最大弯振耦合应力得到了有效的减小。