柔性Rushton搅拌桨的振动特性

2021-05-15杨锋苓曹明见张翠勋刘欣

化工学报 2021年4期

杨锋苓，曹明见，张翠勋，刘欣

（1 山东大学机械工程学院，山东济南250061； 2 高效洁净机械制造教育部重点实验室（山东大学），山东济南250061；3山东大学机械工程国家级实验教学示范中心，山东济南250061； 4 山东天力能源股份有限公司，山东济南250100）

引言

对于流体搅拌混合而言，增强混合效果、提高混合效率是永恒的主题，新型桨的研发是实现这一目标的主要手段。自从20 世纪50 年代Nester[1]提出柔性搅拌桨的概念以来，该类型桨的研究备受重视。搅拌过程中，通过柔性桨叶与流体间的耦合作用，有助于增强能量的传递，强化流体混合。

迄今为止，国内[2-13]及国外[14-24]学者采用理论分析、数值模拟和实验测试的方法对不同类型及材质的柔性搅拌桨的流场、变形、混合进行了研究。课题组前期基于标准Rushton 搅拌桨，以橡胶为材料制作了柔性叶片，代替原有的刚性平直叶片的外伸段，设计了一种实验室规模的柔性叶片Rushton 搅拌桨。该桨能根据操作条件及搅拌介质的不同，通过自主变形获得适宜的外形，具有自适应特性。前期工作中，分别以不同浓度的甘油-水溶液和纯水为介质，数值模拟并实验测试了该桨的流场与功耗特性[25]，并实验测试了介质为水时的混合性能[26]。与标准Rushton 桨的对比发现，该柔性桨能改善流场结构，降低搅拌能耗，缩短混合时间，提高混合效率。本工作是该系列研究的第三部分，分析柔性叶片Rushton 搅拌桨的固有频率、振型、谐响应等振动特性，并探讨转速和介质的影响规律，为后续的放大设计及工业应用奠定基础。

与刚性桨叶相比，柔性桨叶的密度小、质量低，导致在进行模态特性实验测试时，粘贴的加速度传感器的质量相对较大；使用力锤敲击柔性叶片时，更容易发生连击现象；此外，在测量转动状态下的振动特性时，一般的振动测试仪体积较大，无法随着柔性搅拌桨同步转动，给实验测试带来了难度。鉴于以上问题，本文采用微型加速度传感器以减少其质量的影响，选用模态力锤以尽可能地减少连击现象，采用微型数据采集仪代替一般的振动测试仪，实现采集仪器和柔性叶片Rushton 桨的同步转动，实时记录搅拌过程中的加速度数据，以提高实验测试结果精度。此外，还采用流固耦合的数值模拟方法研究柔性叶片Rushton 搅拌桨的振动特性，与实验测试结果进行对比。

1 实验装置

本文中所研究的搅拌系统与前期工作中[25-26]采用的系统一致(图1)，搅拌容器是无挡板圆柱形有机玻璃槽，内径T=300 mm，液位高度H=T。搅拌桨为柔性叶片Rushton 桨，直径D=T/2，离底高度c=H/3，桨叶宽度l=20 mm，长度w=50 mm，其中与圆盘连接段为刚性桨叶，长度w1=15 mm，外端粘接柔性桨叶，长度w2=35 mm，桨叶及圆盘厚度δ=2 mm，搅拌轴直径d=20 mm。柔性桨叶材料为NBR3604 丁腈橡胶，弹性模量7.8 MPa，泊松比0.47，密度1000 kg·m-3；搅拌轴、圆盘和刚性桨叶材质为06Cr19Ni10 结构钢，密度7850 kg·m-3，弹性模量2×105MPa，泊松比0.3。实验介质为常温水，转速N=2 s-1。为了便于实验结束后排空液体，搅拌容器底部略具有少许的弧度，可近似看作平底。搅拌容器底部的支撑装置可垂直、水平调节搅拌容器的位置，精度为1 mm，以便保证搅拌轴和搅拌容器的中心轴线重合，同时保证搅拌桨的离底高度。考察转速和介质对振动特性的影响时，具体参数见表1。由表中Reynolds 数的大小可知，介质为水时，容器内流体处于湍流状态；介质为不同纯度的甘油-水溶液时，容器内流体处于层流状态。

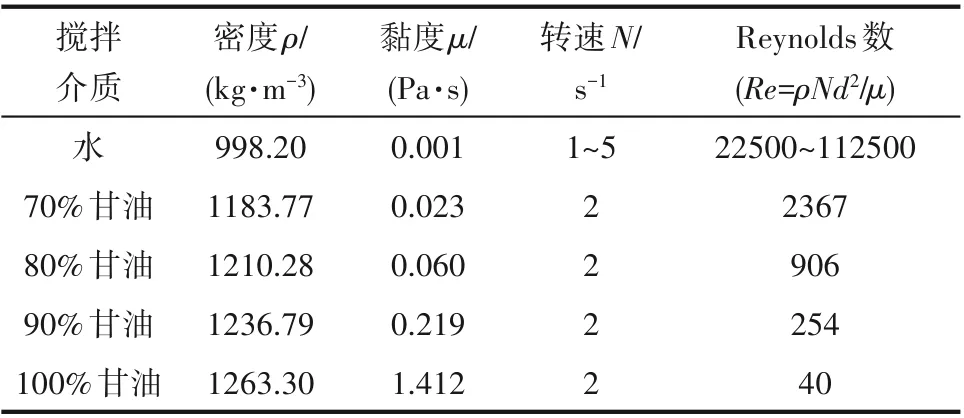
表1 流体物性参数及搅拌桨转速和Reynolds数Table 1 Fluid physical parameters，impeller rotational speed and Reynolds number

图1 搅拌实验装置及搅拌桨Fig.1 Experimental set-up and impeller

2 数值模拟

采用流固耦合的方法模拟柔性叶片Rushton 搅拌桨的流场，提取流体作用在搅拌桨和搅拌轴上的压力，然后在ANSYS Static Structural 分析模块中导入压力，再利用Workbench Modal 模块，采用Block Lanczos法，即模态叠加法，对桨轴系统的固有频率、振型、谐响应特性进行分析。

2.1 几何建模及网格划分

采用Solidworks 软件建立搅拌桨和搅拌轴的三维几何模型，利用ANSYS的DesignModeler模块通过布尔运算生成流体域，包括包含搅拌桨的转子和搅拌容器内除转子外其他流域的静子两部分。利用ANSYS Fluent Meshing 划分网格，静子采用MultiZone 方法，网格类型选六面体；转子及固体域采用Patch Conforming Method 方法，网格类型选四面体，其中搅拌轴网格尺寸为2 mm，圆盘、轮毂和刚性叶片网格尺寸为1 mm；柔性叶片网格类型选六面体，尺寸为1 mm。固体域的网格单元总数为277773个，网格质量为0.83（该值最大为1，越接近1网格质量越好）。

为了兼顾模拟精度和计算量，需要对流体域的网格进行独立性分析，共划分了coarse、medium 和fine三种不同密度的网格，具体信息见表2。以转速N=2 s-1为例，选取不同网格密度时搅拌容器中间纵截面内、搅拌桨所在轴向高度处流体的速度沿径向坐标r 的分布情况进行对比，以考察网格对模拟结果的影响，结果如图2所示。需要说明的是，径向位置r=0～10 mm 和r=25～75 mm 分别被搅拌轴和搅拌桨所占据，因此没有流体速度分布。由图可以看出，基于coarse 网格的模拟精度较低，而基于medium 和fine 网格的速度模拟结果吻合较好。鉴于此，选用medium 网格开展后续的模拟工作，划分情况见图3。

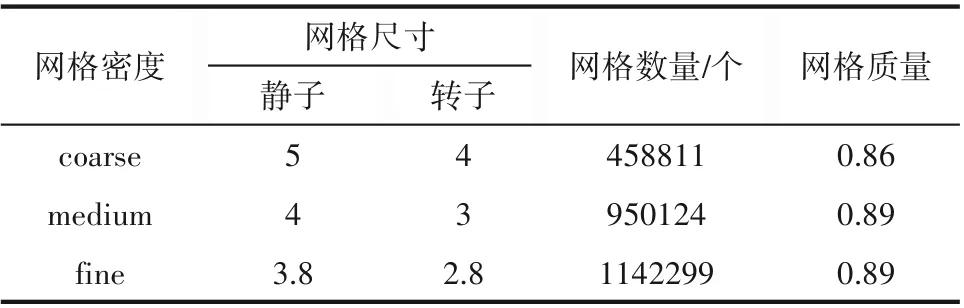
表2 流体域网格Table 2 Grids of the fluid zones

2.2 控制方程

流体域的质量守恒方程为：

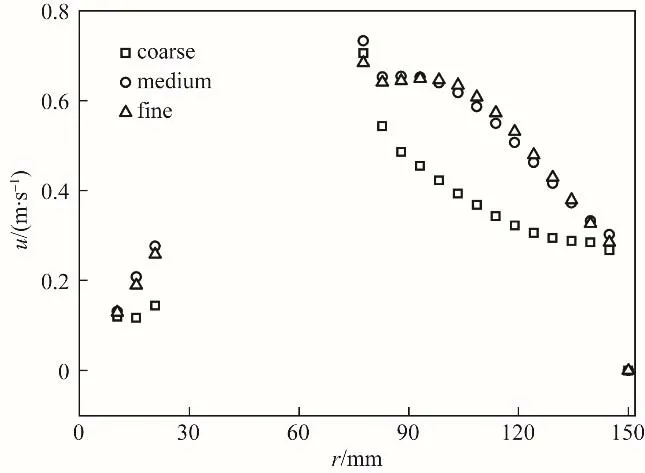
图2 网格独立性分析Fig.2 Grid independence test

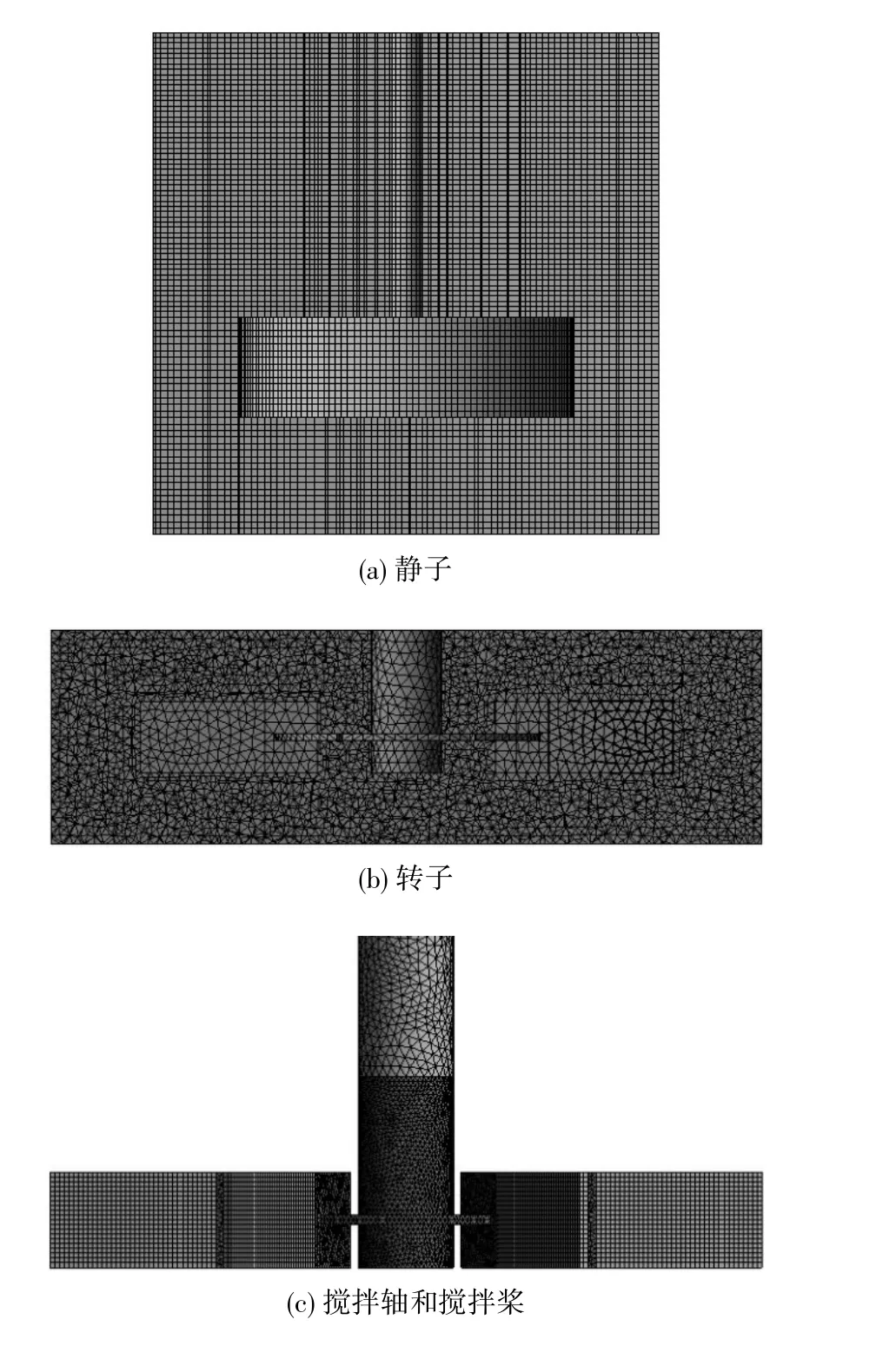
图3 搅拌系统网格划分Fig.3 Grids of the stirred system

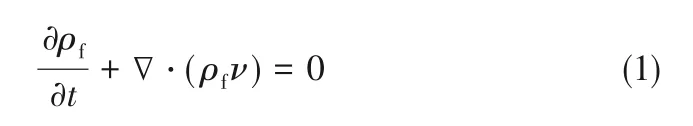
动量守恒方程为：

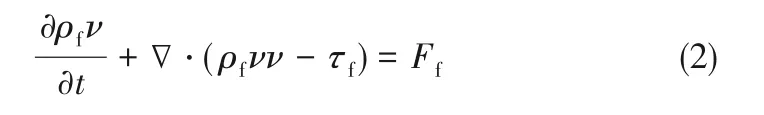
式中，ν 是流体的运动黏度，Ff是流体体积力，τf是流体剪应力：

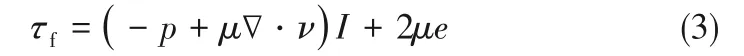
式中，p是流体压力，e是速度应力张量：

固体域的控制方程为：

式中，s是位移，σs是正应力，Fs是固体体积力。

流固耦合交界面处，应力、位移满足守恒关系：

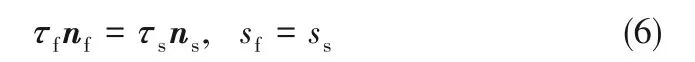
式中，τs为固体剪应力，nf和ns分别为流体和固体界面的法向位移矢量。

求得施加在桨轴系统上的流体作用力后，即可采用交错迭代法求解如下流固耦合振动方程[27]，分析该系统的振动特性：

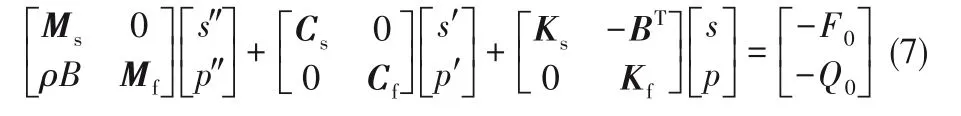
式中，Ms为结构质量矩阵，Mf为流体附加质量矩阵，B 为系数矩阵，Cs为结构阻尼矩阵，Cf为流体附加阻尼矩阵，Ks为结构刚度矩阵，Kf为流体附加刚度矩阵，F0为外界激励，Q0为流体附加激励。

2.3 边界条件及模拟设置

采用压力基绝对速度稳态求解器，分别使用laminar和标准k-ε湍流模型模拟搅拌容器内的层流和湍流流场。利用多重参考系法模拟搅拌桨的旋转，近壁区采用标准壁面函数。转子和静子交界面设为Interface 边界，搅拌容器内壁面和底面设为无滑移静止壁面，搅拌轴和搅拌桨外表面设为无滑移运动壁面，自由液面设为对称边界。控制方程采用二阶迎风格式进行离散，压力速度耦合采用SIMPLE 算法，变量收敛残差设为10-3。干模态分析时不考虑预应力的影响，湿模态分析时则需要考虑重力、系统旋转产生的离心力及流体对桨轴系统产生的压力等预应力的作用。对于固体域，搅拌桨顶部设为固定约束，对搅拌桨施加相应的旋转速度，考虑重力的影响，同时将流体域的压力计算结果施加到搅拌桨和搅拌轴上。以介质为水、转速N=2 s-1为例，桨轴系统的约束设置及流体压力的导入分别如图4和图5所示。

3 实验测试

分别采用丹麦的Brüel&Kjær 和中国的东华振动测试仪开展桨轴系统的干模态和湿模态实验，研究系统在空气中静止及水中旋转时的振动特性。

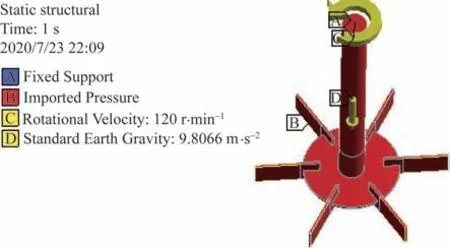
图4 桨轴系统约束设置Fig.4 Constraint settings of the shaft and impeller

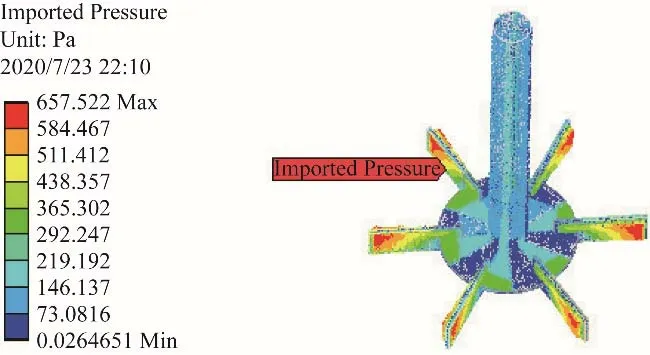
图5 桨轴系统的流体压力导入Fig.5 Imported fluid pressure on the shaft and impeller

3.1 干模态实验

如图6 所示，采用单点激振法对桨轴系统进行干模态试验，实验装置由BK 振动测试仪、力锤、加速度传感器及PL 数据处理软件组成。振动测试仪的型号为3560-C，量程是25 kHz，主要功能是连接力锤、加速度传感器及PL软件，组成振动测试系统，测量采集振动数据。力锤产于美国PCB 公司，型号是086C03，主要功能是给桨轴系统施加外部激励，可有效地减少谐振和连击现象。加速度传感器产于美国Dytran 公司，型号是3035B，灵敏度为98.35 mV·g-1，重1 g，测试时固定在桨叶上。PL 软件用于振动测试数据的分析和处理，可得到频域特性曲线及桨轴系统的各阶固有频率。

实验开始之前，先使用连接线将BK 振动测试仪分别与力锤、加速度传感器及PL 软件正确连接，然后接通电源，打开PL 软件，通过“激活-开始-触发”步骤进行检查，确保系统能正常工作。进行实验时，首先通过“激活”操作，使BK振动测试仪和PL软件进入待采集状态，并使PL软件的力和响应记录均进入可测量范围；其次单击“开始”，随即使用力锤向桨轴系统施加激励，此时要保证作用时间短，尽力避免连击；然后点击“触发”，BK 振动测试仪即开始采集实验数据，数据处理软件对数据进行处理，得到频域特性曲线和固有频率。

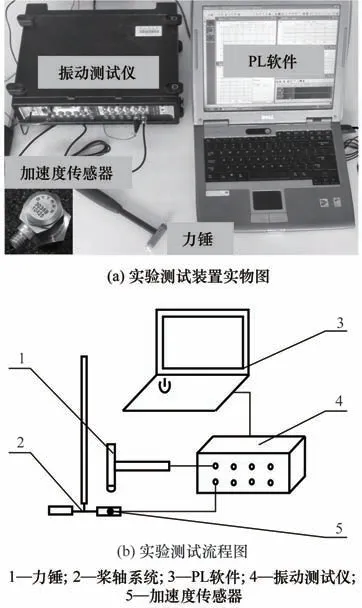
图6 干模态实验测试装置及流程图Fig.6 Dry-modal experimental measurement apparatus and schematic diagram

3.2 湿模态实验

实验装置如图7所示，采用DH5916型动态数据采集仪，选用单通道离线模式进行连续采集，叶片振动特性的测量采取自由振动法。1A803E 型加速度传感器(重1 g)可采集桨叶在不同转速下的加速度数据，动态数据采集仪(重约100 g)可采集并存储由加速度传感器测得的加速度信号，得到时域特性曲线，再借助DHDAS 动态信号分析系统进行快速傅里叶变换后得到频域特性曲线，并进一步分析桨轴系统的固有频率。

实验前要将加速度传感器粘贴至被测量桨叶(重10 g)，将无线通讯式动态数据采集仪固定在搅拌轴(重1000 g)上以便保持同步转动，用USB 通讯线将其与计算机连接，并打开该仪器，进行接口和参数设置，就绪后即可断开USB 通讯线准备实验。实验时，需重启动态数据采集仪，然后启动搅拌桨，依次长按DH5916 仪器上的“平衡-采样-停止”按钮，测量指定转速下的振动数据。实验结束后，打开DHDAS动态信号分析系统，将动态数据采集仪从搅拌轴上拆下后使用USB 通讯线连接至计算机，进行实验数据的回收、分析和处理。

图7 湿模态实验测试装置Fig.7 Wet-modal experimental measurement apparatus

4 结果与讨论

4.1 数值模拟结果

4.1.1 固有频率对桨轴系统进行干模态和湿模态分析后，得到前24 阶固有频率如表3 所示。湿模态分析时，与实验测试时一样，介质为水，搅拌桨转速N=2 s-1。由表3 可知，就各阶固有频率的大小而言，干模态及湿模态条件下，各阶固有频率均存在明显的“集聚”现象，即每6 阶固有频率分布在一个大致相同的数值附近。原因在于柔性Rushton 桨共有6片桨叶，而且均匀地分布在圆盘上，整个桨轴系统是对称的,求解振动方程所得到的固有频率有多重根。就固有频率的变化趋势而言，与干模态分析相比，湿模态分析得到的各阶固有频率均有不同程度的降低：第1～6 阶和第7～12 阶固有频率的下降比例依次为2.25%～2.42%和2.05%～2.16%，而第13～18 阶和第19～24 阶固有频率下降的比例只有0.46%和0.02%左右，表明湿模态时的预应力对低阶固有频率的影响要大于高阶。

模态分析得到的固有频率可用于计算桨轴系统的临界转速，以便使实际转速避开临界值，避免共振。随着固有频率阶次的增加，对应的振型越复杂，振动响应越小，危险程度越低[28]。因此，模态分析得到的低阶固有频率对于研究和实际生产更具有参考意义和实用价值。由表3 可知，桨轴系统的第13 阶固有频率已高达150.280 Hz，实际搅拌转速远低于这一频率值，从这一点来看，分析高阶振型也没有必要。为此，下一节中主要分析桨轴系统的前12 阶振型，对比分析桨轴系统的变形特性。

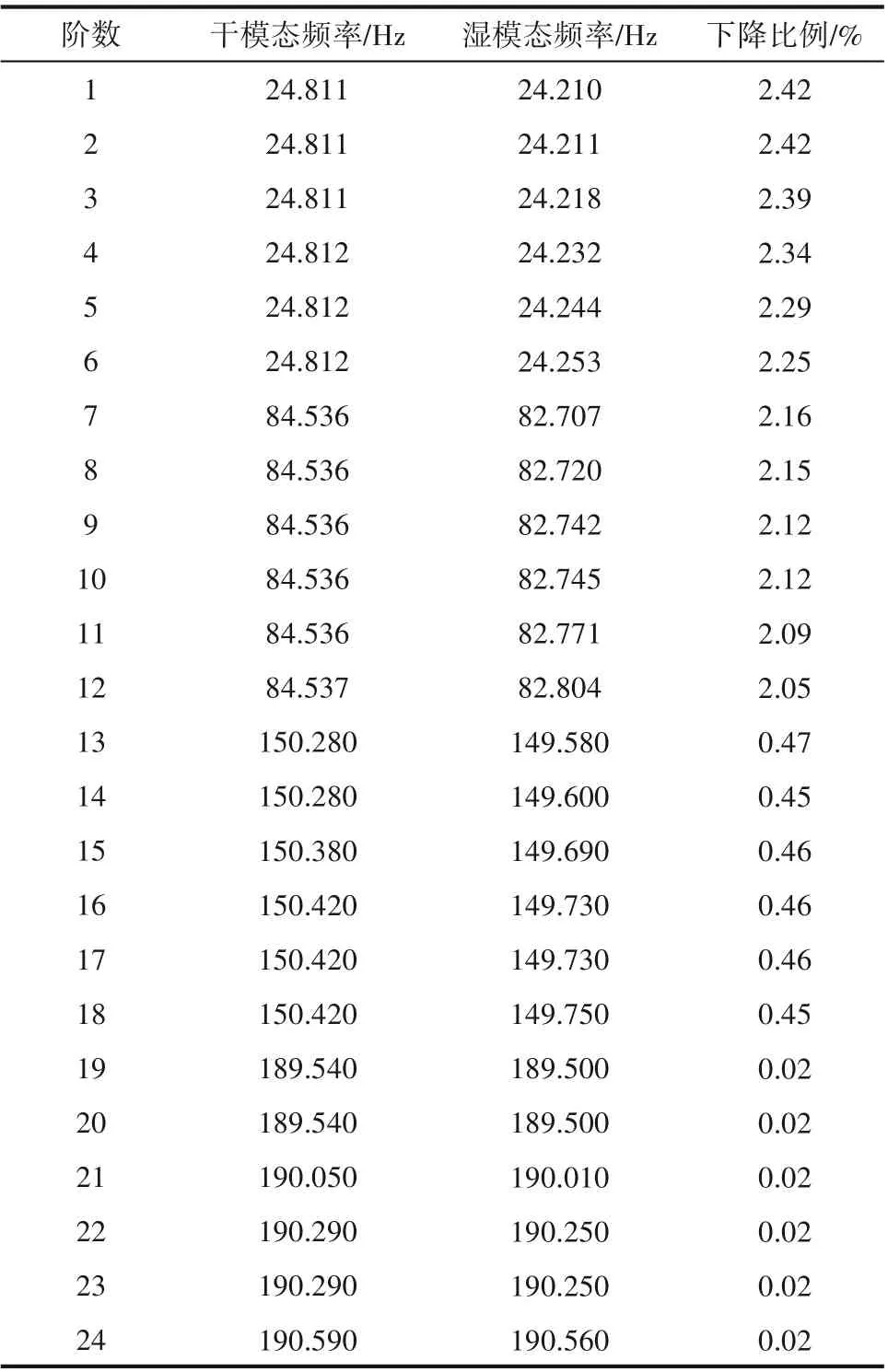
表3 桨轴系统干模态和湿模态固有频率的模拟结果Table 3 The numerically obtained dry-modal and wetmodal natural frequency of the shaft and impeller

4.1.2 振型图8 为柔性叶片Rushton 桨的前12 阶干模态(左列)和湿模态(右列)振型对比，为了便于描述各阶振型的变化情况，对6 片桨叶按逆时针方向依次进行编号，最左侧的桨叶为1号。可以看出，干模态和湿模态时第1～6 阶振型均为弯曲型，第7～12阶均为扭转型。这意味着低转速时柔性Rushton 桨叶只发生弯曲变形，由桨叶中部到尾端变形逐渐增大；转速达到一定值后，柔性桨叶将发生严重的扭转变形，在实际操作中需要避免。就变形量而言，与干模态相比，湿模态时各阶振型的变形量均有不同程度的增大。干模态时，最大弯曲和扭转变形分别发生第4 阶和第8 阶；湿模态时，最大弯曲和扭转变形分别发生第4阶和第7阶，其中第8阶振型的变形量和第7 阶几乎完全一致。需要说明的是，在搅拌过程中，桨叶的实际变形量很小，振型图中的变形量是模态位移，为相对值，没有实际量化意义，仅用于定性地考察比较[29]。

对比干模态和湿模态时的各阶振型还可发现，相同阶数时变形桨叶的编号并不同。譬如第1阶振型，干模态时变形主要发生在1 号和4 号桨叶，其他桨叶变形相对较小；湿模态时虽然变形也主要发生在1 号和4 号桨叶，但其他桨叶的变形几乎为零。再以第3 阶振型为例，干模态时6 个桨叶都有一定程度的变形，而湿模态时的变形主要发生在5 号桨叶。高阶振型也存在类似的差异，例如第7阶振型，干模态时2、3、5、6 号桨叶发生明显的扭转，1 号和4号桨叶扭转变形相对较小；湿模态时只有1 号桨叶产生大幅度的扭转，其他桨叶几乎无扭转。对于第12阶振型，干模态时6个桨叶都有明显的扭转变形，而湿模态时只有3号桨叶才存在扭转。

总之，前12阶振型的主要变形发生在柔性桨叶的尾端，刚性桨叶和搅拌轴的变形量远小于柔性桨叶。对于弯曲型振型，最大变形遍布于柔性桨叶的尾端；对于扭转型振型，最大变形位于柔性桨叶尾端的两侧叶角，且上下两部分变形基本对称。对于干模态振型，不同阶数时振型相位的差别是造成桨叶的相对变形存在差异的关键原因[30]；对于湿模态振型，与相同阶数的干模态振型相比，预应力及柔性桨叶与搅拌介质之间的流固耦合作用是引起变形差异的根本所在。此外，振型反映的未必是桨轴系统的实际振动形态，后者是各阶振型相叠加的结果。

4.1.3 谐响应特性通过模态分析求得桨轴系统的各阶固有频率后，可以给系统施加不同频率的随时间按正弦规律变化的周期性交变激励载荷进行谐响应分析。谐响应分析可用来判断某种载荷下是否发生共振现象，以便使实际工作载荷避开系统的固有频率，保证安全运转。

根据模态分析得到的固有频率结果，并适当扩大频率范围，选择10～500 Hz 的频段进行谐响应分析，所得到的应力和应变频率响应曲线如图9所示。图中f 为外部激励频率，σ 表示应力，ε 表示应变。由图可知，激励载荷频率为206 Hz 和255 Hz 时，桨轴系统有明显的应力和应变响应。据表3 可知，引起桨轴系统产生显著应力、应变响应的外部激励的频率均高于系统的前24 阶固有频率，属于高阶频段。因此，为了避免搅拌系统产生较大的外部激励响应，工作载荷应避开高阶固有频率。需要说明的是，对于不同频率的外部激励载荷，桨轴系统发生共振时的响应形式未必相同，对应着最大应力或最大应变，即应力和应变最大值对应的是桨轴系统不同阶次的固有频率，在数值上并不相等。这就是图9 所示的响应曲线中应力和应变最大值对应的频率不一致的内在原因。

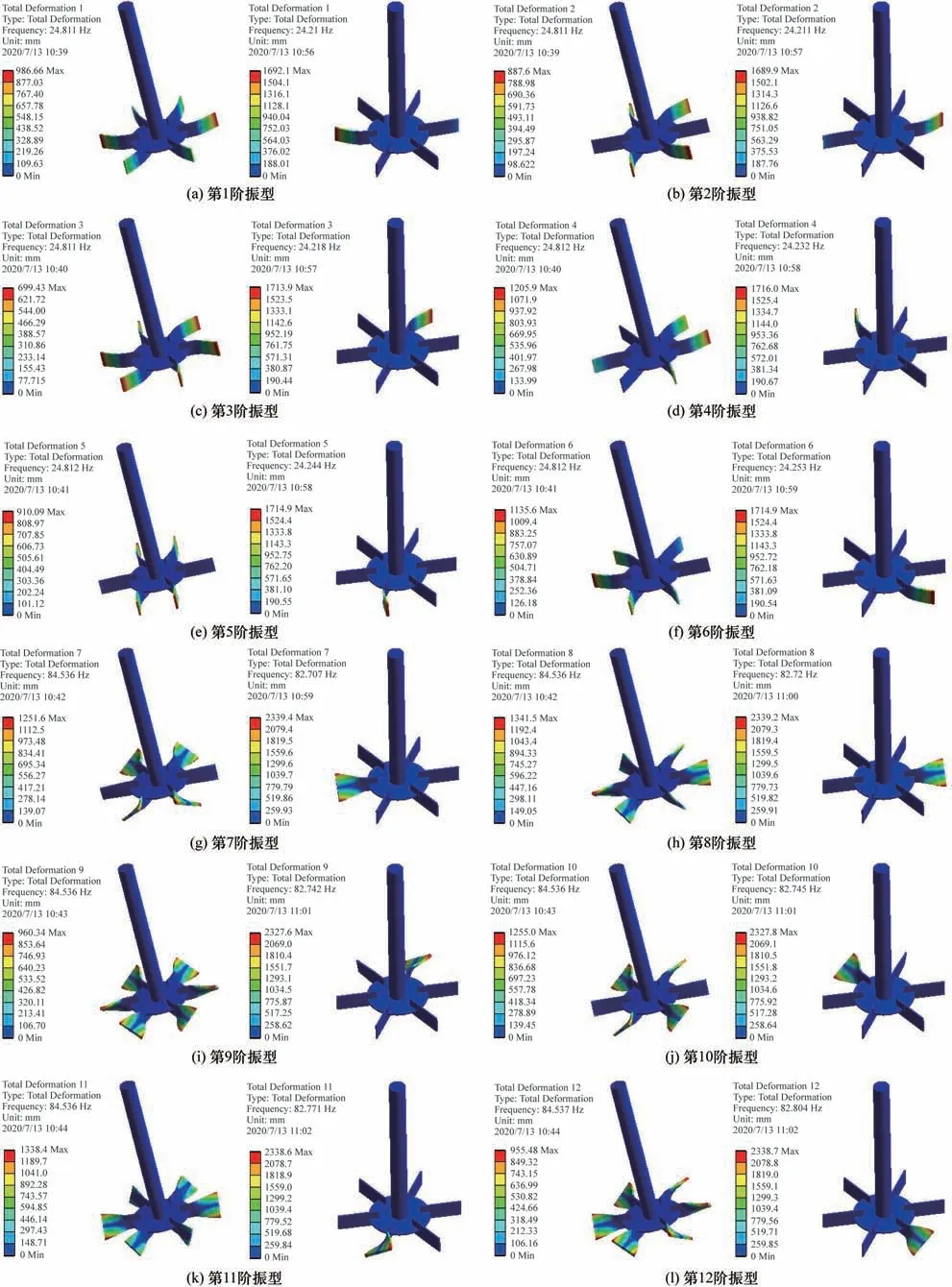
图8 桨轴系统的前12阶干模态(左列)和湿模态(右列)振型Fig.8 The first 12 dry-modal(left)and wet-modal(right)vibration modes of the stirred shaft and impeller

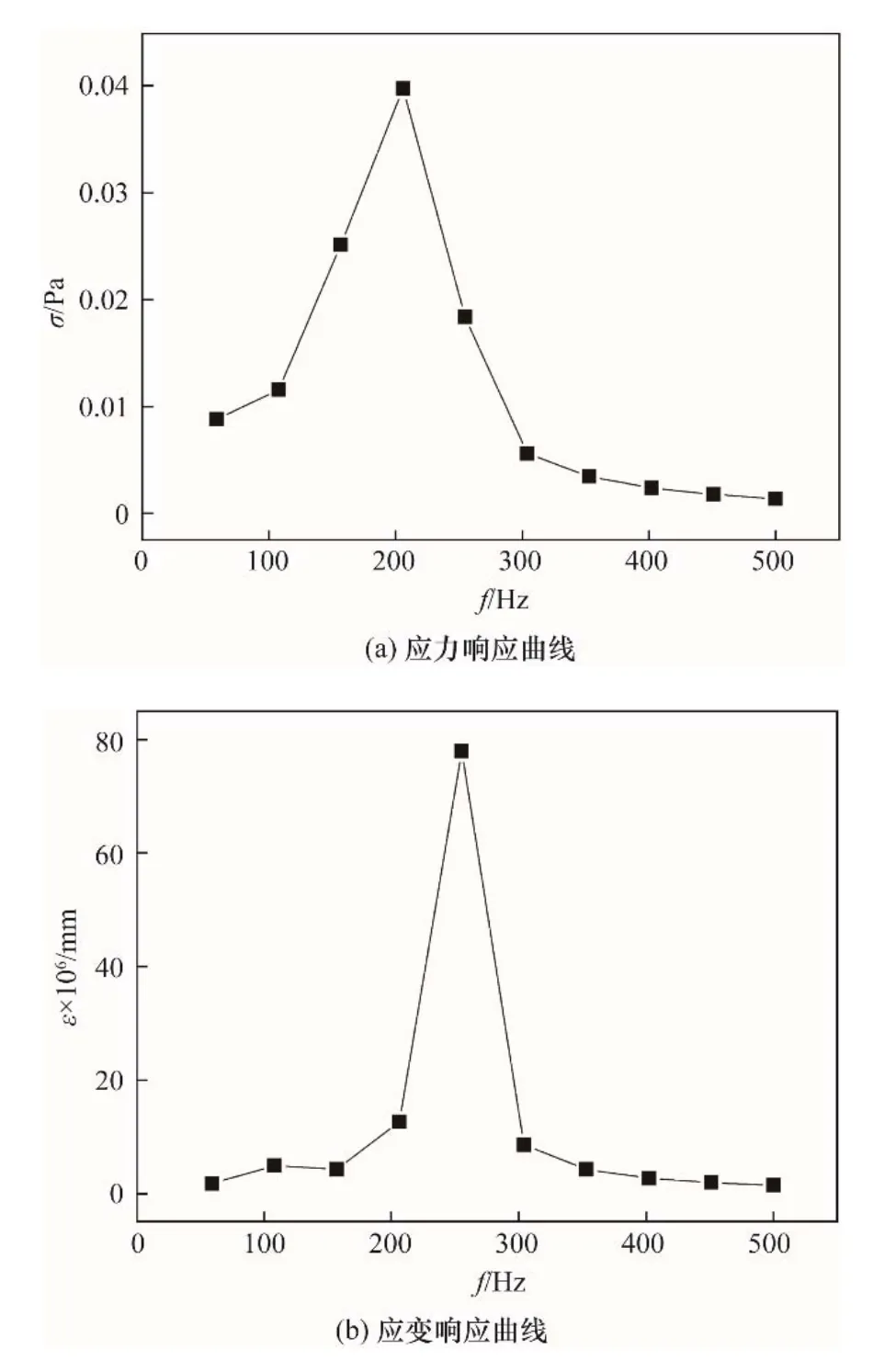
图9 外部激励下桨轴系统的应力应变响应曲线Fig.9 The stress and strain response curves of the shaft and impeller system under the external excitation loads

4.2 实验测试结果

4.2.1 干模态实验结果利用PL 软件，处理BK 振动测试仪采集的数据，得到加速度a 对频率的响应特性曲线如图10 所示。由图可知，第7～12 阶固有频率比第1～6 阶固有频率的响应明显，而且存在显著的集聚现象。利用PL 软件对实验数据进行处理，得到干模态实验的阻尼比为5.11%。表4 列出了前12 阶固有频率的实验结果及其与模拟结果的对比。由表可知，桨轴系统第1～6 阶及第7～12 阶固有频率分别集聚在24.000 Hz 和82.000 Hz，与实验结果相比，模拟结果分别偏高3.38%和3.09%。诚然，实验结果也存在一定误差，主要有两个来源：一是加速度传感器质量的影响，二是模态力锤敲击时的连击现象，尽管已竭力避免，但仍存在一定的影响。

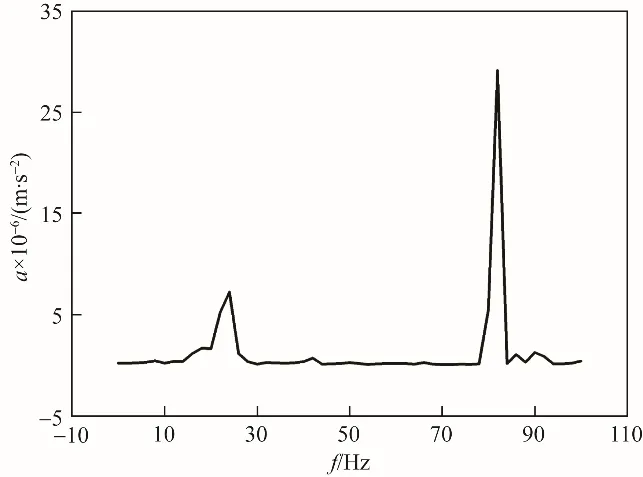
图10 干模态频域特性曲线Fig.10 The dry-modal frequency domain characteristic curve

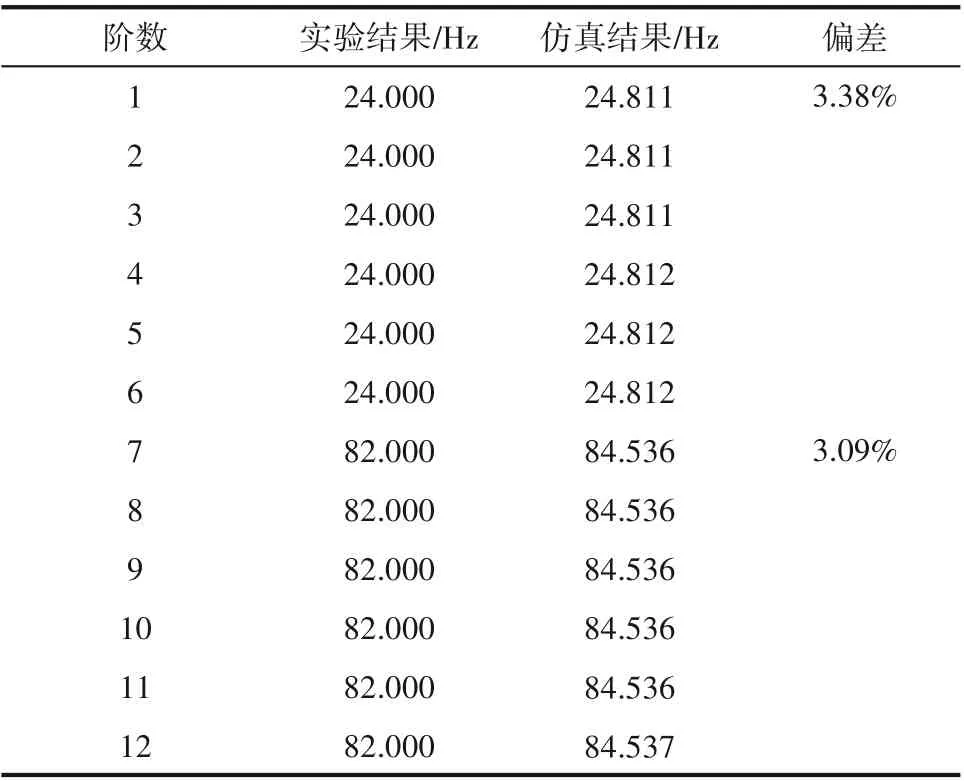
表4 干模态固有频率的实验及模拟结果对比Table 4 Comparison between the experimental and numerical results of the dry-modal natural frequencies

4.2.2 湿模态实验结果实验测得的湿模态频域特性曲线见图11，与模态实验结果相比，此时的集聚现象也很明显。此外，湿模态时阻尼比的实验结果为7.07%，与干模态相比，湿模态时具有更高的阻尼比，说明搅拌桨在水中受到的阻尼比在空气中大。需要指出的是，湿模态频域特征曲线与静止桨轴系统在空气中的干模态频域特征曲线的响应规律正好相反，第1～6 阶固有频率的响应比第7～12阶固有频率显著，原因在于阻尼的增加导致桨轴系统损耗更多的能量，阻尼对桨轴系统高阶固有频率影响大于低阶，从而使得低阶固有频率对于激励的响应更加显著。

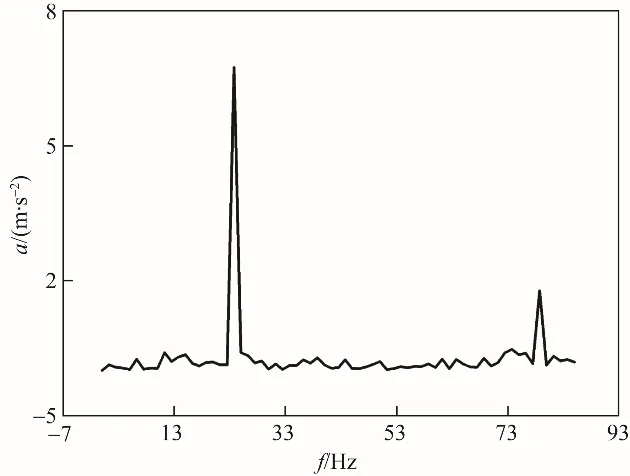
图11 湿模态频域特性曲线Fig.11 The wet-modal frequency domain characteristic curve

表5 为前12 阶固有频率的湿模态实验结果，与干模态实验结果相比，各阶湿模态的固有频率均有所降低，该趋势与数值模拟结果一致。此外，桨轴系统的前6 阶固有频率集聚在23.750 Hz，模拟结果比该实验值偏高1.94%～2.12%；第7～12 阶固有频率集聚在78.750 Hz，相比之下，仿真结果偏高5.02%～5.15%。实验误差主要来源于DH5916 数据采集仪及加速度传感器的质量对桨轴系统的影响，受测量方法的限制，这是不可避免的。

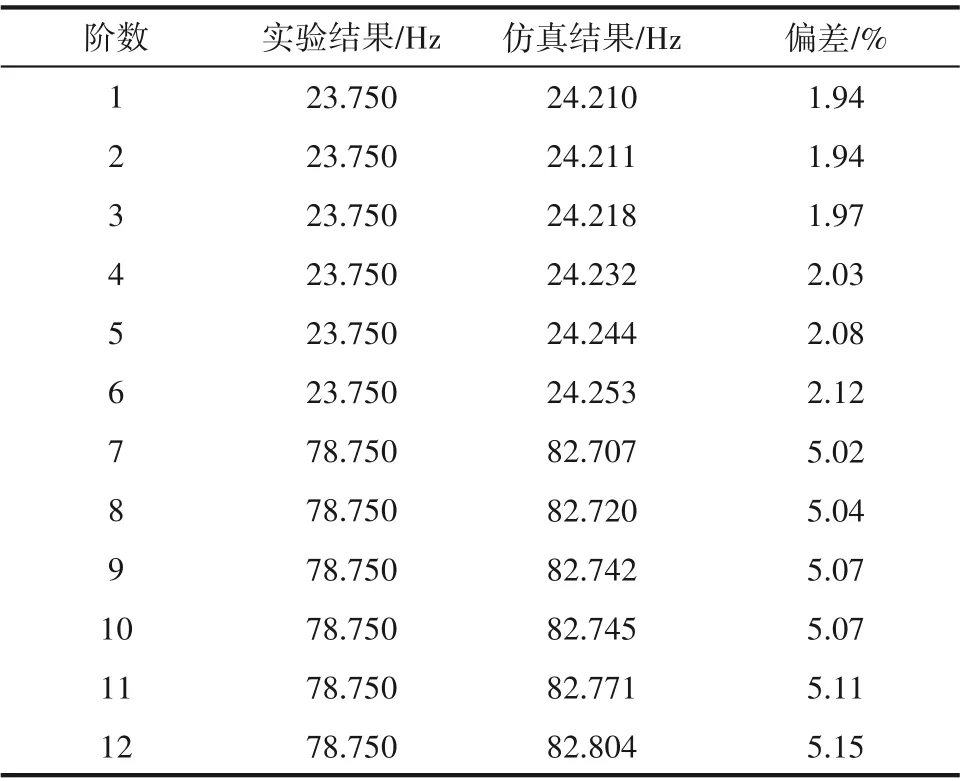
表5 湿模态固有频率的实验及模拟结果对比Table 5 Comparison between the experimental and numerical results of the wet-modal natural frequencies

4.3 转速及介质的影响

4.3.1 转速的影响以水为介质，考察搅拌桨转速分别为1、2、3、4 和5 s-1时的前12 阶湿模态特性，发现前6 阶振型仍为弯曲型，后6 阶仍为扭转型。不同转速下的各阶固有频率如表6 所示，转速为2 s-1时的结果见表5 第3 列，此处不再列出。由表可知，相同转速时桨轴系统的前12阶固有频率仍然是每6阶集聚一次，任意一阶固有频率都随转速的增大而减小，转速越高减小的幅度越大。原因在于搅拌桨的旋转对系统的刚度产生了“旋转软化”效应，转速越高软化作用越大，系统刚度越小，固有频率也越低[28]。

表7 给出了各阶固有频率随转速的变化比例。随着转速的增加，各阶固有频率的下降比例均不断增大，转速由1 s-1等幅增至5 s-1时(增幅为1 s-1)，桨轴系统第1～6 阶固有频率的下降比例范围依次为2.09%～2.23%、6.13%～6.72%、14.21%～16.00%、36.24%～41.63%；类似地，第7～12 阶固有频率的下降比例范围依次为1.83%～1.92%、4.99%～5.31%、10.83%～11.60%、22.29%～23.91%。上述结果说明，高转速对固有频率的影响比低转速明显，就相同转速变化范围而言，转速对低阶固有频率影响更大。

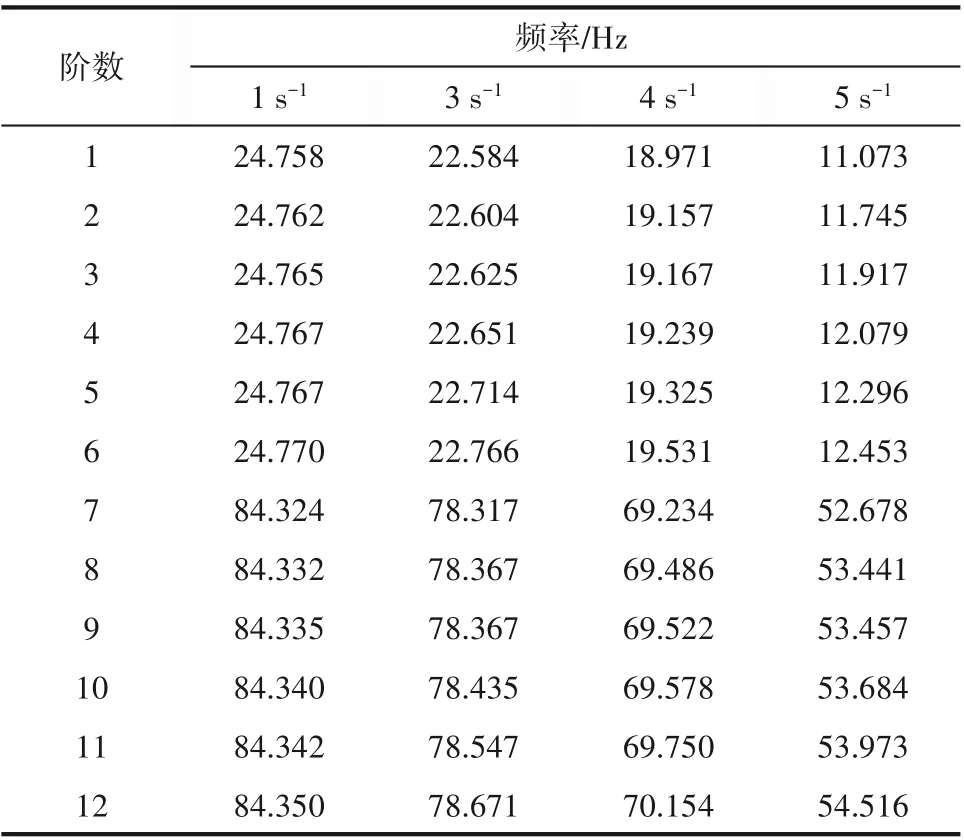
表6 不同转速时桨轴系统的固有频率Table 6 Natural frequencies of the shaft and impeller system at different rotational speeds

4.3.2 介质的影响本节中，分析搅拌介质为纯水及不同纯度(具体信息见表1)的甘油-水溶液时柔性叶片Rushton 桨轴系统的前12 阶湿模态特性，此时前6 阶振型仍为弯曲型，后6 阶仍为扭转型。不同纯度甘油的密度与水接近，而黏度却有显著的差别，因而能体现介质黏度对桨轴系统固有频率的影响。

黏度影响到桨轴系统的阻尼，导致不同介质时系统的固有频率存在差异，结果见表8，其中介质为水时的固有频率见表5 第3 列。横向比较可知，桨轴系统的任意一阶固有频率均随介质黏度的增大而增大，增加的比例如表9 所示。对于第1～6 阶固有频率，当搅拌介质由水到纯甘油时，随着黏度的增加，固有频率增加的比例越来越大，大约由1.12%增大到8.06%；不同的是，对于第7～12阶固有频率，随着介质黏度的增大，固有频率增加的比例先增大后减小，变化范围为0.41%～1.89%。就固有频率增加的幅度而言，也具有相同的趋势。以上结果表明，介质黏度对低阶固有频率的影响更大。

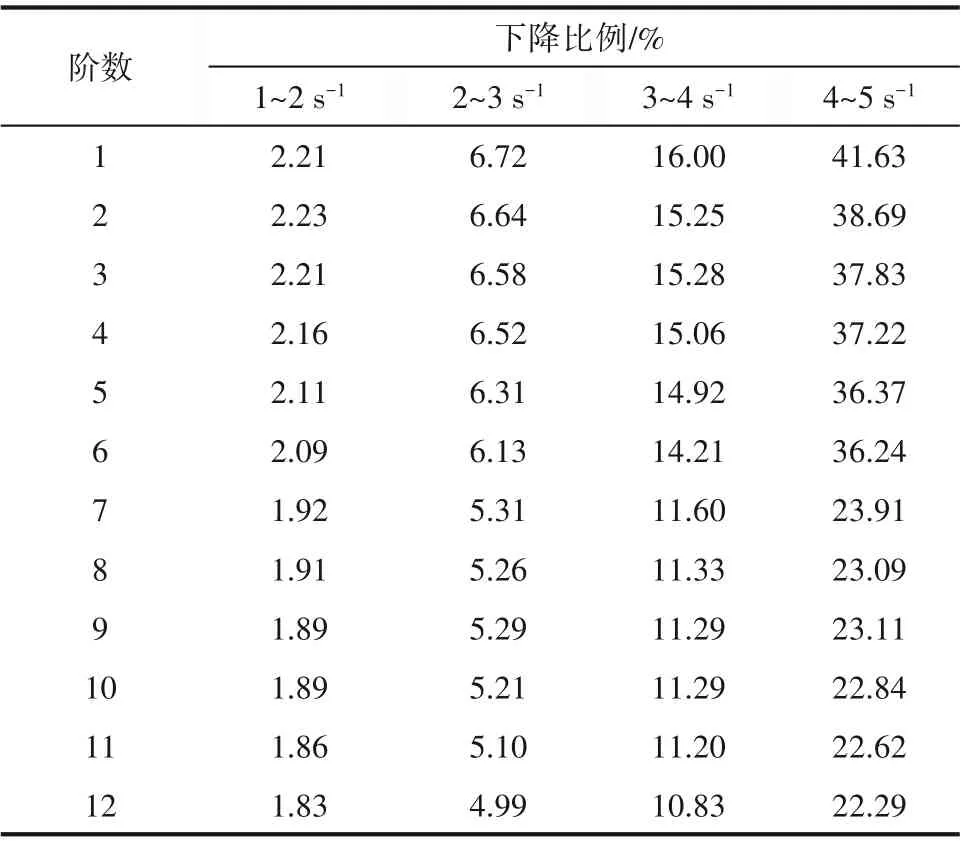
表7 转速增加时桨轴系统固有频率的下降比例Table 7 The decrease ratios of natural frequencies with the increase of rotational speeds

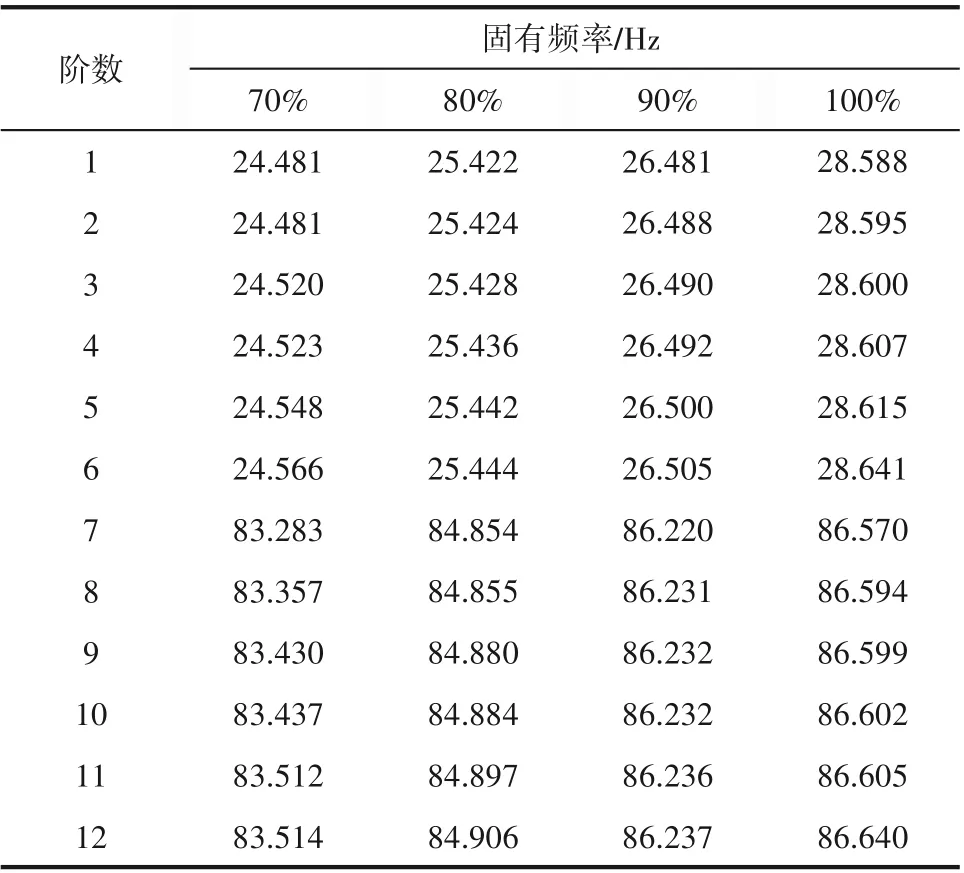
表8 不同纯度的甘油时桨轴系统的固有频率Table 8 Natural frequencies of the shaft and impeller system for different glycerine solutions

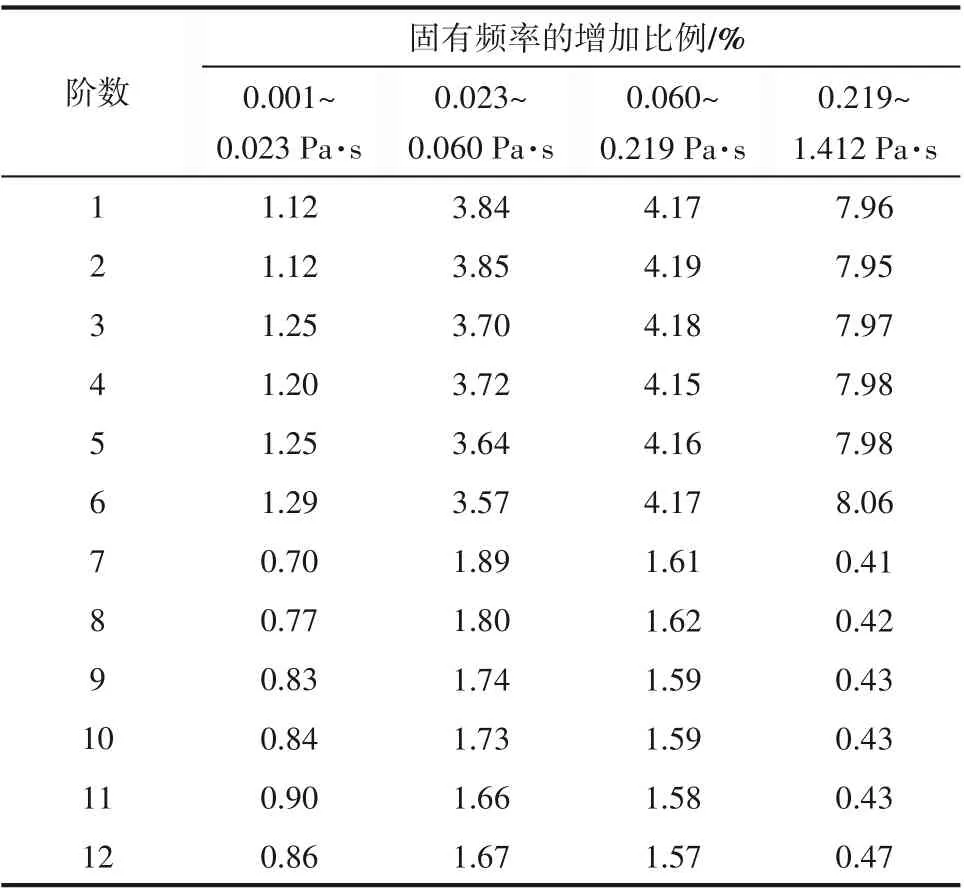
表9 介质黏度增大时桨轴系统固有频率的增加比例Table 9 The decrease ratio of natural frequencies with the increase of rotational speeds

5 结论

采用数值模拟与实验测试相结合的方法，研究了柔性叶片Rushton 搅拌桨的振动特性，并分析了转速和介质的影响规律，得到以下结论。

(1) 柔性叶片Rushton 桨轴系统前24 阶固有频率的分布存在集聚现象，每6 阶发生一次集聚。与干模态固有频率相比，各阶湿模态固有频率均有不同程度的下降。

(2) 所研究的工况下，柔性Rushton 桨轴系统的振型是系统的一种固有属性，与转速和介质无关，第1～6阶为弯曲型，第7～12阶为扭转型。

(3) 当外部交变激励载荷频率高于柔性叶片Rushton 桨轴系统的前24 阶固有频率时，存在明显的应力和应变谐响应。为此，工作载荷的激励频率应避开高阶固有频率，以保证搅拌设备正常运行。

(4)柔性叶片Rushton桨轴系统的固有频率随转速的增大而下降，转速越高下降的幅度及比例越大，相同转速变化范围内，转速对低阶固有频率的影响更大。随着介质黏度的增大，桨轴系统第1～6阶固有频率增加的幅度及比例越来越大，第7～12阶固有频率增加的幅度及比例先增大后减小，介质黏度对低阶固有频率的影响更显著。

符号说明

a——加速度，m·s-2

B——系数矩阵

C——刚度矩阵

c——离底高度，m

D——搅拌桨直径，m

d——搅拌轴直径，m

e——速度应力张量

F——体积力，Pa

F0——外界激励，Pa

f——频率，Hz

H——液位高度，m