椭偏高斯光束经过非线性介质后的远场衍射图样

陶 智，彭楚楚，邓罗根

(北京理工大学 物理学院，北京 100081)

1 引 言

高斯光束入射非线性介质后，由于介质的三阶非线性效应会引起入射光相位分布发生变化，在远场产生明暗相间的衍射圆环，该现象被称为空间自相位调制现象。空间自相位调制现象由于其在材料非线性折射率的测量[1-2]、非线性光限幅器的设计[3]以及中空激光束的产生[4]等方面有着极大的应用价值而受到广泛关注。最早由Callen等人[5]在实验中观察到。此后，人们相继在液晶[6-8]、原子蒸汽[9]、聚合物[10]以及纳米复合材料[11]等非线性材料系统中观测到类似的现象，区别仅在于衍射环的数目不同、图样中心的斑点在一些实验中是亮斑，而在另一些实验中是暗斑。为了解释这种环状图样的形成机理，早在1981年Durbin等人[12]从空间自相位调制角度很好地解释了实验中出现的环状衍射图样，并给出了衍射环数和最大附加相移间的定量关系。1997年，Harrison研究小组[13]在实验中发现，当高斯光束经过一个薄的吸收型自散焦介质时，会在远场形成中心恒为暗斑的衍射图样。次年，他们研究小组[14]利用耦合场物质方程对上述现象给出了理论分析，并得出结论，远场暗斑的稳定存在是波前曲率和空间自相位调制共同作用的结果。2005年，Deng等人[15]系统研究了自聚焦、自散焦介质对发散、会聚高斯光束的作用，总结了不同远场环状图样出现的条件，他们认为当波前曲率和附加相移的乘积的符号为正时，远场会出现中心是亮斑的环状衍射条纹，而当波前曲率和附加相移的乘积的符号为负时，远场衍射图样的中心是暗斑。此后，人们在研究工作中发现，样品的位置[16]、介质的非局域性[17]、入射光场的频率、能量等因素[18]均会对远场衍射图样的形成产生影响。值得一提的是，尽管之前人们对空间自相位调制现象的研究取得了一系列成果，但是他们没有考虑当入射非线性介质的光是偏振光时，非线性介质对不同偏振光响应的差别。事实上，早在上世纪60年代初，Maker等人[19]在研究液晶折射率随强度变化的工作中就已指出，对于同一各向同性非线性介质，椭圆偏振光的左旋圆偏振分量和右旋圆偏振分量引起的非线性折射率不同。Boyd[20]也曾在书中明确给出线偏振光、圆偏振光以及椭圆偏振光在非线性介质中的非线性折射率的表达式。

本文以衍射理论为基础，建立了偏振态为椭圆偏振的高斯光束(椭偏高斯光束)经过非线性介质后远场光强分布的理论模型。采用数值方法，研究了椭偏高斯光束入射非线性介质后的远场光强分布图及衍射图样。进一步研究发现，入射光场的椭偏率是影响远场光强分布的重要因素，并且非线性机制不同，椭偏率对远场光强分布的影响也不同。

2 理 论

设椭偏高斯光束经过一个薄的线性吸收型各向同性非线性介质，那么，介质入射面上光场的琼斯矢量可以表示为

(1)

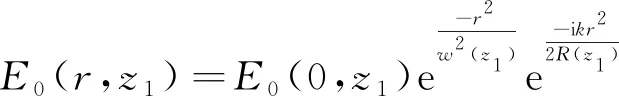
E(r,z1)=E+σ++E-σ-，

(2)

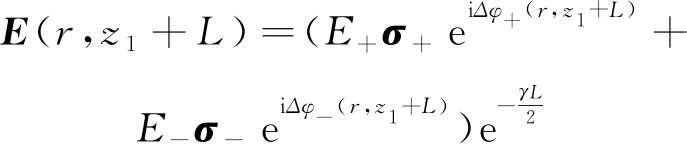
(3)

式中:γ为非线性介质的线性吸收系数，Δφ+(r,z1+L)和Δφ-(r,z1+L)分别代表左旋圆偏振光及右旋圆偏振光在介质出射面处对应的附加相移[15]，可分别表示为

(4)

(5)

式中:Δn+和Δn-分别为左旋圆偏振光及右旋圆偏振光在非线性介质内对应的非线性折射率。由参考文献[19]可知，

(6)

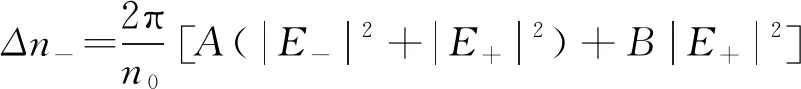
(7)

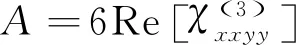
(8)

当e=0时，入射光为线偏振光；当e=1时，入射光为左旋圆偏振光；当e=-1时，入射光为右旋圆偏振光。此时，式(6)、(7)可统一表示为

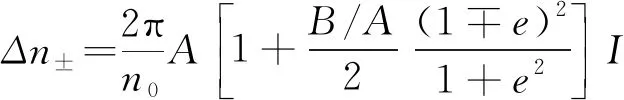
(9)

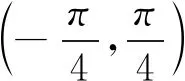
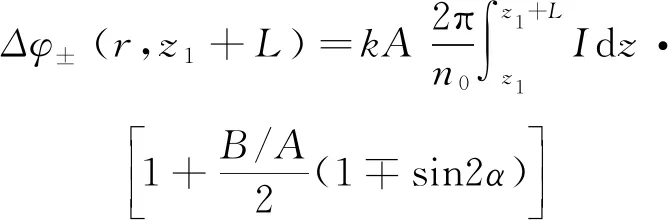
(10)

根据文献[20]，式中B/A可代表引起非线性折射率的非线性机制，B/A=0代表电致伸缩或热致非线性机制，B/A=1代表非共振电子非线性机制，B/A=6代表分子取向非线性机制。由朗伯(Lambert)定律可知,在介质内部，光强与z的关系可近似为

I(r,z)=I(r,z1)e-γ(z-z1)，

(11)

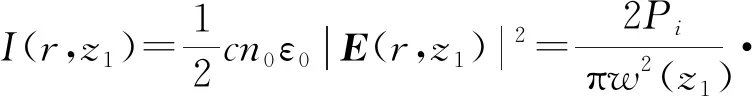
(12)

令

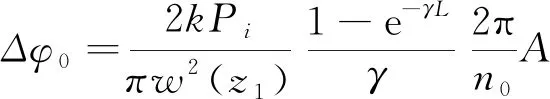
(13)

(14)

则式(12)可写为

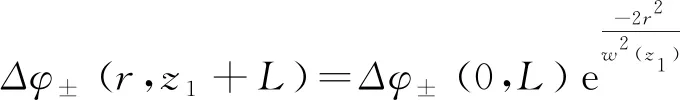
(15)

其中：Δφ±(0,L)表示介质位于z1位置时椭偏高斯光束在介质出射面产生的峰值非线性相移。Δφ0表示在B/A=0或入射光为圆偏振光的情况下产生的相移，本文中，我们称它为“原相移”。利用基尔霍夫-夫琅禾费远场衍射公式[22]，我们可以得到远场衍射后的场强为

(16)

式中：J0(krθ)是第一类零阶贝塞尔函数，D是样品与观察屏之间的距离。为积分方便，将E(r,z1+L)做正交分解，写为两个线偏振分量Ex和Ey的叠加形式，

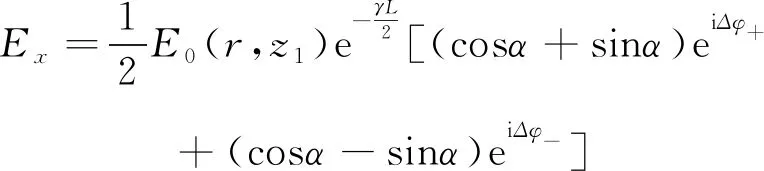
(17)

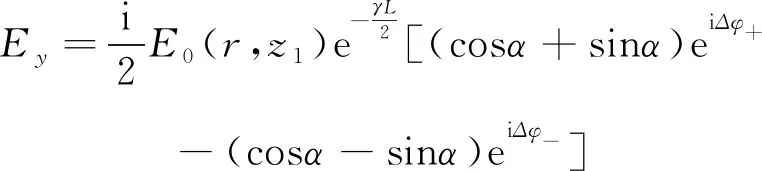
(18)

分别计算Ex和Ey在远场的光强分布Ix和Iy，设远场探测孔径的半径为ρ，考虑光强，则

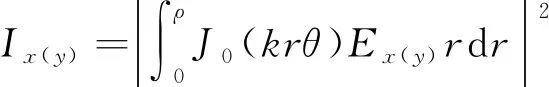
(19)

相应地，远场衍射总光强I=Ix+Iy。

3 模拟结果及分析

以下我们将利用式(19)对椭偏高斯光束经过非线性介质后的远场光强分布及衍射图样进行数值模拟。由理论部分可知，椭偏率e是影响椭偏高斯光束经过非线性介质后的远场衍射图样的一个重要因素，本文将着重探究其在远场衍射图样形成过程中的作用。模拟程序中所选固定参数为λ=532 nm，w(z1)=1 mm，Δφ0=4π，R(z1)=2 m。

图1(a)、(c)、(e)是在电致伸缩非线性机制或热致非线性机制(对应于参数B/A=0)情况下，椭偏率e分别取0.4，0.6，0.8时椭偏高斯光束通过非线性介质后的远场光强分布图，横坐标表示远场衍射角，纵坐标表示光强。图1(b)、(d)、(f)是与图1(a)、(c)、(e)相对应的远场衍射图样。模拟结果显示，在电致伸缩非线性机制下，远场光强的x分量对总光强的贡献随着椭偏率e的增大而减小，y分量的贡献随椭偏率的增大而增大。二分量叠加后，远场总光强的分布不随椭偏率的改变而改变。总光强最亮环的光强约为0.97，中心暗斑的光强约为0.11。相应地，不同椭偏率的椭偏高斯光束入射非线性介质在远场形成的衍射图几乎样完全相同，如图1(b)、(d)、(f)所示。图样中心均为暗斑，暗斑外围均有3个亮环，2个暗环，且最外侧的亮环光强强度最大。该现象说明，当引起介质非线性折射率的机制是电致伸缩非线性机制时，椭偏率对远场衍射光强分布的影响可忽略不计。

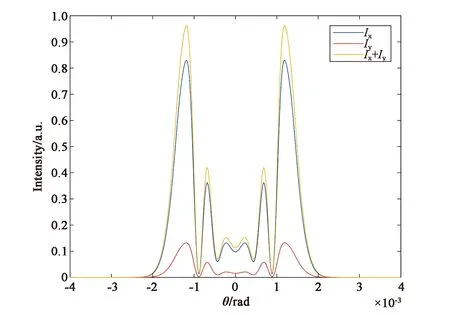
(a) e=0.4时的远场光强分布图(a) Far-field intensity distribution with e=0.4

(b) e=0.4时的远场衍射图样(b) Far-field diffraction pattern with e=0.4

(c) e=0.6时的远场光强分布图(c) Far-field intensity distribution with e=0.6

(d) e=0.6时的远场衍射图样(d) Far-field diffraction pattern with e=0.6

(e) e=0.8时的远场光强分布图(e) Far-field intensity distribution with e=0.8

(f) e=0.8时的远场衍射图样(f) Far-field diffraction pattern with e=0.8图1 B/A=0时，不同椭偏率下的远场光强分布图和远场衍射图样。Fig.1 Far-field intensity distribution and far-field diffraction pattern with different ellipticity while B/A=0

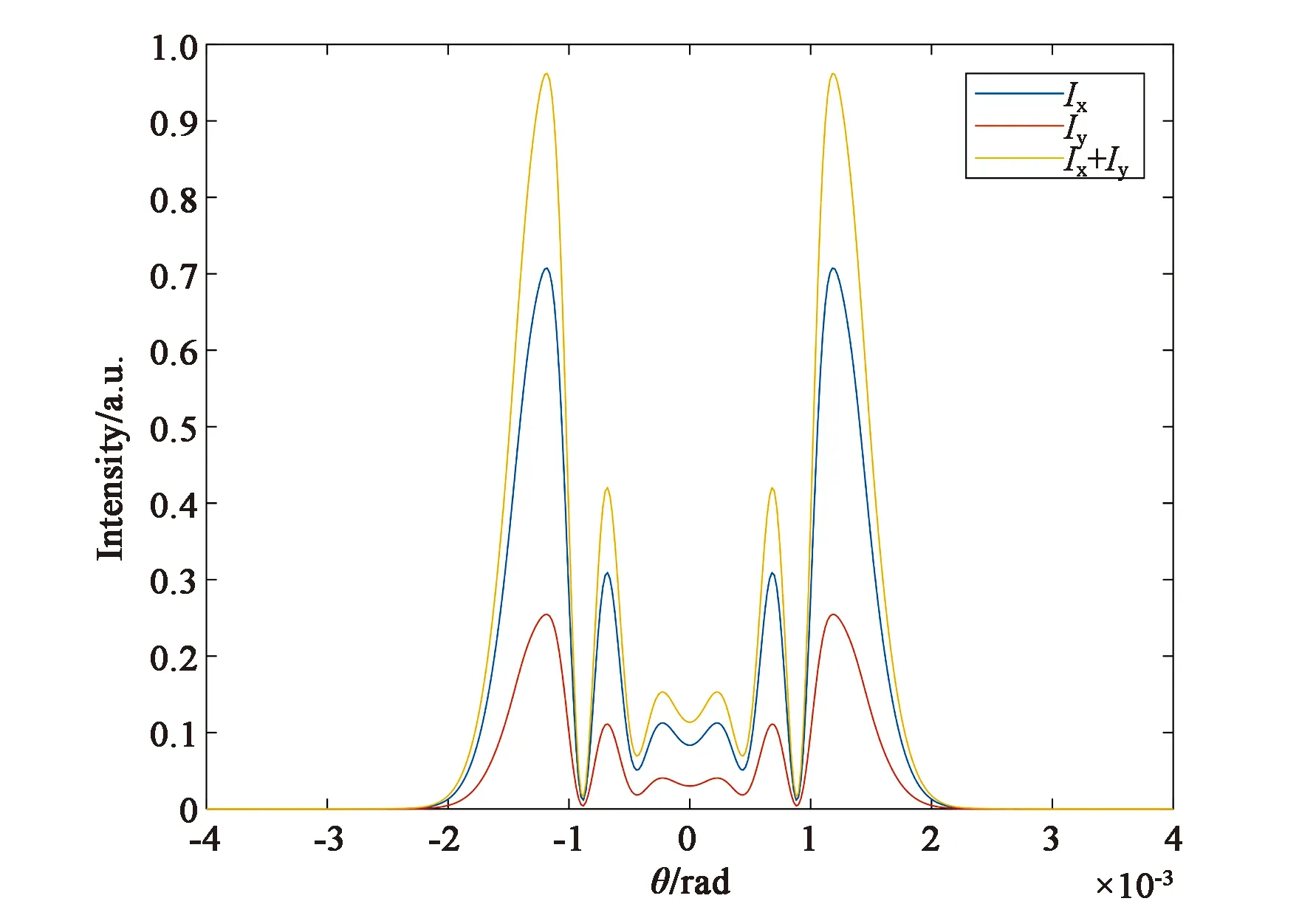
图2(a)、(c)、(e)是在非共振电子非线性机制(对应于参数B/A=1)情况下，椭偏率e分别取0.4，0.6，0.8时椭偏高斯光束通过非线性介质后的远场光强分布图。从图中可以看到，在非共振电子非线性机制下，随着椭偏率的增大，x分量和y分量发生同步变化，表现为光场分布半径变小，中心斑点半径变小，中心斑点外围最亮环的光强变强。总光强随之发生相同的变化。e=0.4时，总光强的光场半径约为e=0.8时的1.5倍。e=0.4时，总光强最亮环的光强最小，约为0.68。e=0.6时，最亮环光强约降为0.80。e=0.8时，总光强最亮环的光强最大，约为0.95。由此可知，当引起介质非线性折射率的机制是非共振电子非线性机制时，椭偏率的增大会导致远场光强分布半径和中心斑点分布半径变小，光能更多地分布在衍射外环。图2(b)、(d)、(f)是与图2(a)、(c)、(e)相对应的远场衍射图样。

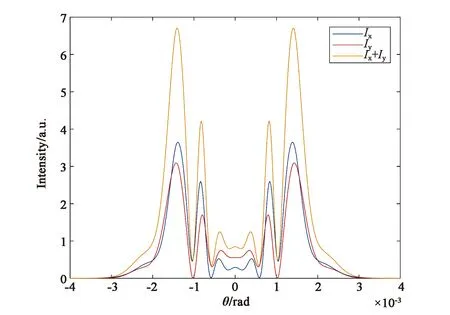
(a) e=0.4时的远场光强分布图(a) Far-field intensity distribution with e=0.4

(b) e=0.4时的远场衍射图样(b) Far-field diffraction pattern with e=0.4

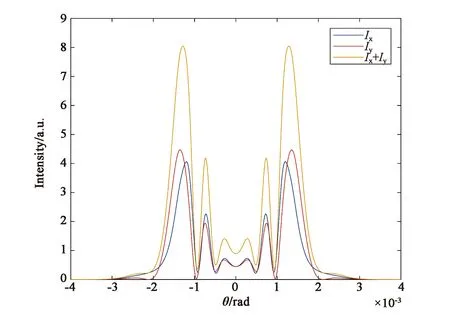
(c) e=0.6时的远场光强分布图(c) Far-field intensity distribution with e=0.6

(d) e=0.6时的远场衍射图样(d) Far-field diffraction pattern with e=0.6

(e) e=0.8时的远场光强分布图(e) Far-field intensity distribution with e=0.8

(f) e=0.8时的远场衍射图样(f) Far-field diffraction pattern with e=0.8图2 B/A=1时，不同椭偏率下的远场光强分布图和远场衍射图样。Fig.2 Far-field intensity distribution and far-field diffraction patterns with different ellipticity while B/A=1

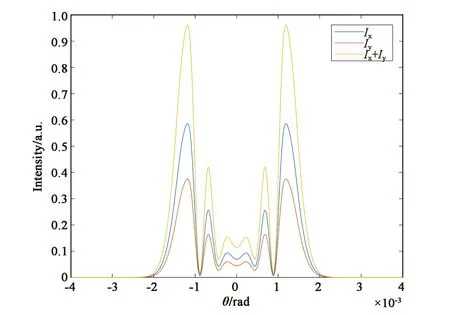
图3是分子取向非线性机制(对应于参数B/A=6)情况下，不同椭偏率的椭偏高斯光束通过非线性介质后的远场光强分布图及衍射图样。从图中可以看到，当e=0.4时，总光强的分布与二分量的光强分布一致，中央光斑均为亮斑，且中心光强最强，约为1.27。中心外围有4个亮环，4个暗环。当e=0.6时，x光强分量与y光强分量中心光强最强。相应地，总光强的中心光强也最强，约为1.27。然而，此时，总光强中心斑点外围的衍射亮环和暗环较e=0.4时均减少1个，并且光场分布半径变小。当e增大至0.8时，二分量的分布半径继续减小，衍射暗环数目减少，中心光强变弱，最外衍射环的光强最强。此时，总光强的分布随之发生同步变化。图(b)、(d)、(f)为图(a)、(c)、(e)各自对应的远场衍射图样，从衍射图样可以明显看到，当B/A=6时，椭偏率的增大不仅会影响图样的分布尺寸和衍射环数目，还会影响图样中心斑点的亮暗。

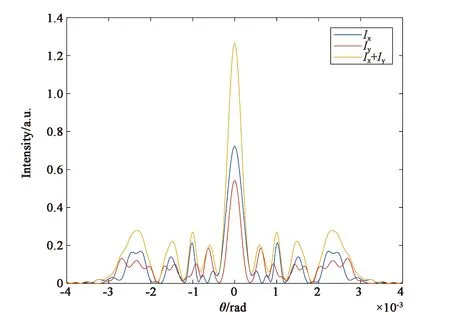
(a) e=0.4时的远场光强分布图(a) Far-field intensity distribution with e=0.4

(b) e=0.4时的远场衍射图样(b) Far-field diffraction pattern with e=0.4

(c) e=0.6时的远场光强分布图(c) Far-field intensity distribution with e=0.6

(d) e=0.6时的远场衍射图样(d) Far-field diffraction pattern with e=0.6

(e) e=0.8时的远场光强分布图(e) The far-field intensity distribution with e=0.8

(f) e=0.8时的远场衍射图样(f) Far-field diffraction pattern with e=0.8图3 B/A=6时，不同椭偏率下的远场光强分布图和远场衍射图样。Fig.3 Far-field intensity distribution and far-field diffraction patterns with different ellipticity while B/A=6

综上可知，椭偏率的改变会导致远场衍射图样的直径、衍射环数以及中心斑点的亮暗发生变化。在不同的非线性机制下，椭偏率的改变会对远场衍射图样产生不同的影响，影响程度的大小随非线性机制对应的B/A数值的增大而增大。在电致伸缩或热致非线性机制下，远场衍射图样几乎不随椭偏率的改变而改变，椭偏率的改变对图样产生的影响可忽略不计。在非共振电子响应非线性机制和分子取向非线性机制下，椭偏率的增大会导致远场衍射图样分布尺寸变小。相比之下，当引起非介质折射率变化的机制是分子取向非线性机制时，远场光强分布对入射光场椭偏率改变的响应更敏感，远场衍射图样的衍射环数和中心斑点的亮暗均会随椭偏率的改变发生明显变化。

4 结 论

综上所述，我们可以得到以下结论：本文建立的计算远场光强分布的理论模型不仅适用于椭偏高斯光束入射非线性介质的情形，通过改变椭偏率e值的大小，还可以得到入射光偏振态为线偏振态、圆偏振态时远场光强的分布模型。处于不同非线性机制下的非线性材料对入射椭偏激光椭偏率变化的响应不同。电致伸缩非线性机制下，椭偏率的变化对椭偏高斯光束经过非线性介质后的远场衍射图样的影响可忽略不计；非共振电子响应非线性机制下，随着椭偏率的增大，远场衍射图样的半径变小、中央光斑半径变小、光场能量更多地分布在衍射外环；分子取向非线性机制下，随着椭偏率的增大，远场衍射图样的半径变小、衍射环数变少、中心斑点由亮斑变为暗斑。根据衍射图样随不同非线性机制的不同演化特征，可以有效区分在强光与非线性介质的相互作用中处于主导位置的非线性机制类型。该结论对非线性机制类型的判断和光限幅器件的设计具有参考意义。