基于包络理论的谐波传动共轭齿廓求解和啮合分析
2021-05-10李鹏超何雪明卢立新林自东
李鹏超 何雪明 卢立新 林自东
(1. 江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122;2. 江南大学机械工程学院,江苏 无锡 214122;3. 山东碧海包装材料有限公司,山东 临沂 276600)
随着机器人技术的快速发展,传统的食品加工工厂向智能化,无人工化迈进。其中,工业机器人是实现智能化食品加工工厂的重点装备,而其中谐波减速器主要作用于工业机器人机械臂的关节处,是影响机器人性能的重要部件之一。谐波减速器由柔轮、钢轮和波发生器组成,其传动主要依靠柔轮的可控的弹性变形来传递运动,通常以钢轮固定,柔轮作为输入,波发生器作为输出来实现运动的传递。
谐波传动中,齿形齿廓是影响谐波减速器高精密度的主要因素,柔轮与钢轮高性能的啮合取决于其齿廓的良好设计。目前关于齿形的研究有图解分析法[1]56-59、等速曲线法[1]61-63、幂级数法[1]63-68、改进运动学法[2]、包络法[3]和速度瞬心法[4]。20世纪50年代由美国学者Musser发明的谐波减速器,所用的齿廓即是直线齿廓,后来被工艺较好的渐开线齿廓代替[1]99-102。Ishikawa等[5]采用齿条近似法简化的方法提出了S型齿廓。辛洪兵[6]在圆弧齿廓的基础上提出了谐波传动双圆弧齿廓的设计方法。王家序等[7-8]对不同共轭原理的双圆弧齿廓谐波传动的共轭齿廓和共轭区域进行了对比分析。张宁等[9]基于柔轮装配后实际齿廓线与理论齿廓线在空间位置上存在差异,为避免啮合干涉或啮合不充分情况,提出柔轮齿廓的修形方法模型来对柔轮齿廓进行设计优化。张雷等[10-12]对双圆弧谐波传动进行啮合优化和仿真分析,探究其柔轮应力的影响规律。肖季常等[13]在基于谐波传动共轭方法的基础上提出三圆弧齿廓的设计方法,并探究三圆弧柔轮齿廓参数对共轭区间的影响。余金宝等[14]根据椭圆凸轮波发生器的运动规律推导柔轮的变形函数,并运用运动轨迹包络求解钢轮齿廓,通过啮合仿真验证所求钢轮齿廓的合理性。前面几篇文献对谐波传动共轭齿廓的求解主要是运用传统的数值解法去推导共轭齿廓,未与运动仿真相结合。余金宝等[14]虽然结合了运动仿真去求解共轭齿廓,但是未考虑柔轮齿在空间的变形情况。
试验拟以公切线式双圆弧齿廓为研究对象,采用包络理论运动学仿真的方法,根据柔轮运动轨迹的包络,对包络线进行最小二乘拟合求解出共轭钢轮齿廓。同时,基于Matlab分析柔轮齿在空间的真实啮合状态调整柔轮齿沿轴向的不同齿高,并在Ansys workbench中建立谐波减速器完整的三维弹性接触模型,分析柔轮的齿根圆半径和加载的转矩对其应力和变形的影响规律,以期优化其参数来降低柔轮的应力,提高柔轮的疲劳强度。
1 谐波传动共轭齿廓设计
1.1 公切线双圆弧齿廓
图1为公切线双圆弧柔轮齿廓坐标系,其由凸圆弧齿廓AB,公切线BC,凹圆弧齿廓CD组成。以柔轮中心线为Y轴,齿廓两侧公切线中点的连线为X轴,则X和Y轴的交点为公切线双圆弧齿廓的坐标原点O。其各段齿廓相应的参数方程表达式为:
(1) AB段凸圆弧齿廓:
(1)
式中:
x1——柔轮凸齿廓横坐标,mm;
y1——柔轮凸齿廓纵坐标,mm;

图1 公切线双圆弧齿廓示意图
ρa——凸圆弧齿廓半径,mm;
α1——凸圆弧角度参数变量,°;
X1——凸齿廓X偏心距,X1=-[ρa-(Sacosα)/2]cosα,mm;
Y1——凸齿廓Y偏心距,Y1=-[ρa-(Sacosα)/2]sinα,mm。
(2) BC段公切线:
(2)
式中:
x2——公切线段横坐标,mm;
y2——公切线段纵坐标,mm;
Sa——齿厚,mm;
α——公切线夹角,°;
l——公切线长度参数变量,mm;
lp——为公切线长度,mm。
(3) CD段凹圆弧齿廓:
(3)
式中:
x3——柔轮凹齿廓横坐标,mm;
y3——柔轮凹齿廓纵坐标,mm;
ρf——凹圆弧齿廓半径,mm;
α2——凹圆弧角度参数变量,°;
X2——凹齿廓X偏心距,X2=(1+sin2α)Sa/2+ρfcosα,mm;
Y2——凹齿廓Y偏心距,Y2=ρfsinα-(Sasinαcosα)/2,mm。
1.2 基于包络理论和运动学仿真的共轭齿廓设计
为表达谐波减速器各构件之间的相对运动关系,以钢轮固定,波发生器输入,柔轮输出建立如图2所示的坐标系统,其中坐标系CG(XG,YG)与钢轮固连,坐标原点OG与谐波传动的回转中心重合,YG为钢轮齿槽的对称线;坐标系CR(XR,YR)与柔轮固连,坐标原点OR为柔轮齿的对称线与柔轮原始曲线SR(原始曲线是指位于受载平面内柔轮的中线在波发生器作用下形成的弹性变形曲线)的交点,YR为柔轮轮齿齿廓的对称线;坐标系C0(X0,Y0)与波发生器固连,坐标原点O0作用在谐波传动的回转中心,与OG重合,Y0与波发生器的长轴重合。
柔轮原始曲线在极坐标下的方程表达式为:
ρ=rm+ω(φ),
(4)
式中:
ρ——柔轮极坐标半径,mm;
rm——柔轮未变形时的半径,mm;
ω(φ)——柔轮径向变形量(以波发生器为标准椭圆波发生器),ω(φ)=ω0cos2φ,mm;

图2 谐波传动转角关系
ω0——柔轮最大径向变形量,mm。
图2坐标系中其余各参数表达式:
(5)
式中:
ν——柔轮的切向变形量,mm;
μ——柔轮轮齿的偏转角,°;
γ——柔轮的转角,°;
U/z1——广义传动比;
U——柔轮的变形波数,取2;
z1——柔轮齿数;
φ——柔轮的YR轴与钢轮的YG轴的夹角,°。
基于包络理论,与柔轮齿廓相共轭的钢轮齿廓表达式为:
(6)
将式(1)~式(5)代入式(6)以求解共轭钢轮齿廓,式(6) 包含有隐函数的偏导求解,其数值解不易求解,通过结合运动仿真可以简化其求解过程。由柔轮坐标系到钢轮坐标系的坐标映射关系,通过Matlab编程,以柔轮的一个单齿相对于钢轮的一个完整的啮入、啮出过程,得到柔轮轮齿相对于钢轮轮齿的运动轨迹,再对运动轨迹中的一系列曲线族进行数学包络,通过最小二乘法拟合曲线族即可求得所需的钢轮齿廓。图3中的粗曲线即为与柔轮齿廓相共轭的钢轮齿廓。
2 公切线双圆弧谐波传动啮合分析
2.1 共轭柔轮空间齿廓计算实例
以模数m=0.311、柔轮齿数z1=160、钢轮齿数z2=162,钢轮固定、波发生器(以椭圆凸轮代替)输入、柔轮输出、单极传动比为80的公切线双圆弧齿廓的谐波减速器为例,柔轮齿廓参数如表1所示。
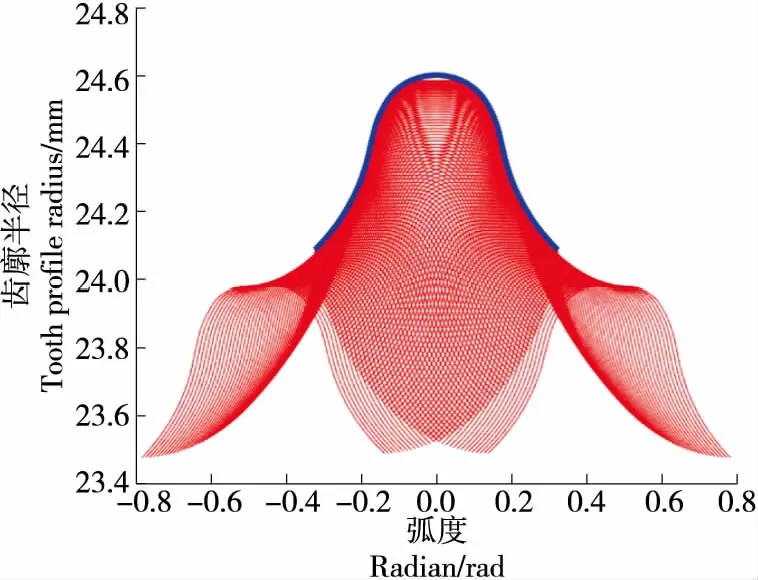
图3 柔轮运动轨迹的包络
图4为一个柔轮齿的沿轴向侧面的齿廓图。由Matlab仿真分析可得修形角β=0.679°,此时共切线双圆弧柔轮齿廓相对于共轭钢轮齿廓啮合轨迹不会发生齿廓干涉现象。图5为柔轮齿齿廓在前端面和后端面的运动轨迹。
2.2 谐波传动三维实体建模
建立谐波传动三维模型,将模型以x_t格式导入Ansys workbench中。柔轮材料选用30 CrMnSiA,材料密度为7 750 kg/m3,弹性模量为1.96×105GPa,泊松比为0.3;钢轮和椭圆凸轮材料选用40#碳素结构钢,材料密度为7 850 kg/m3,弹性模量为2.10×105GPa,泊松比为0.269。选用八节点六面体单元对模型进行网格划分,网格质量的好坏直接影响模型的分析结果,柔轮和钢轮啮合轮齿网格划分应该更为精密,此处选用size为0.6 mm 对柔轮和钢轮齿进行网格加密。波发生器和柔轮内侧壁面的接触size选用1 mm进行加密,其他区域选用2 mm进行网格划分,网格划分效果图如图6所示。
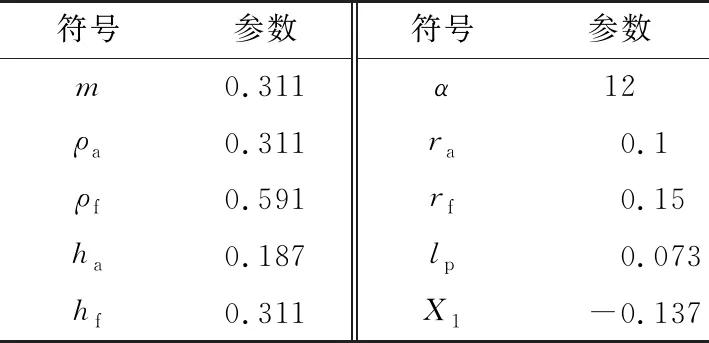
表1 柔轮齿廓参数
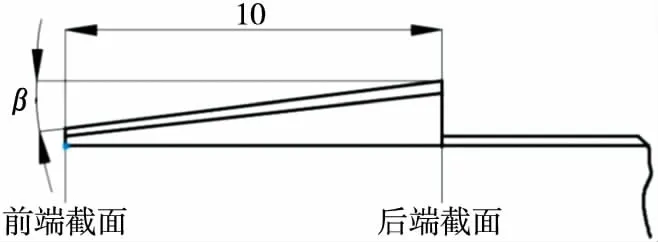
图4 柔轮轴向轮齿修形示意图
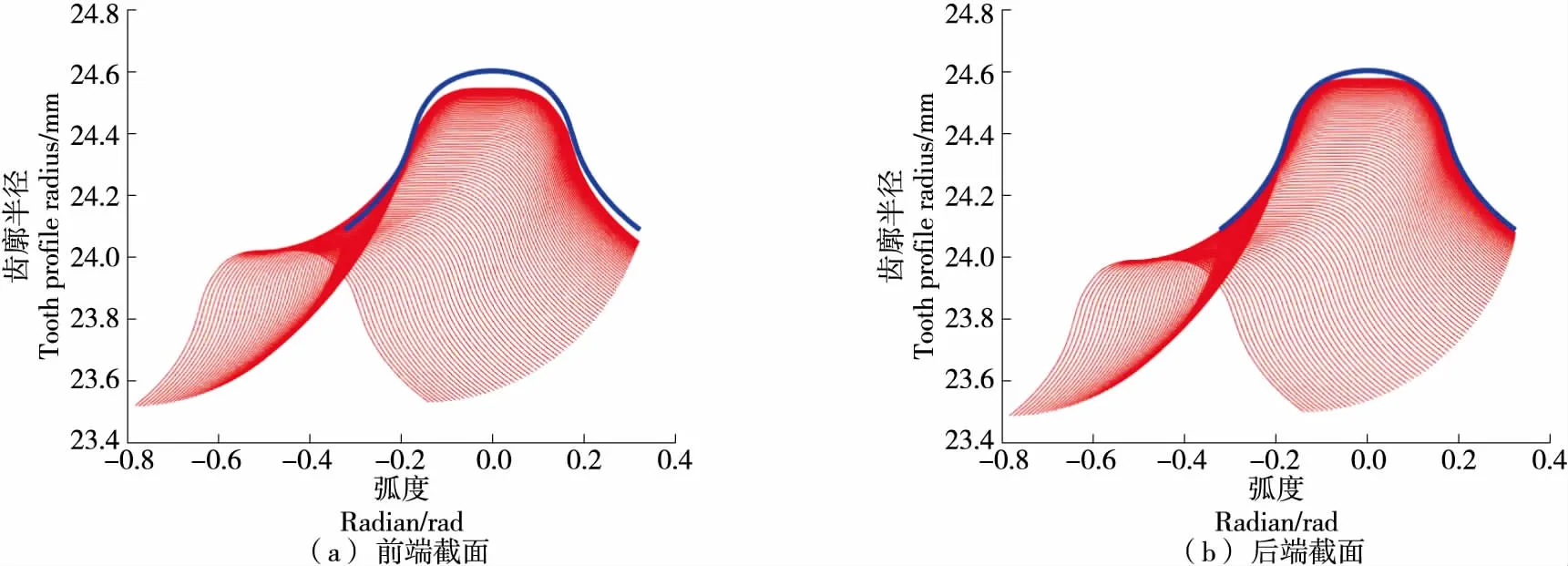
图5 柔轮各截面的运动轨迹
考虑柔轮的结构特点,模型中存在的接触面为:椭圆凸轮的外表面和柔轮内壁表面,椭圆凸轮外表面为“接触面”,柔轮内壁表面为“目标面”;柔轮齿面和钢轮齿面,柔轮齿面为“接触面”,钢轮齿面为“目标面”。接触面的摩擦因数取0.1,钢轮设置固定约束,柔轮和椭圆凸轮设置位移约束(只释放其轴向的旋转约束)。由于柔轮的应力求解为非线性大变形问题求解,所以求解时开启“大变形”设置,同时为提高求解的收敛性,最小增量步调整为109。
2.3 柔轮应力与变形分析
通过Ansys进行谐波减速器的三维弹性接触有限元分析,建立谐波传动3种装配状态:① 柔轮和波发生器装配;② 柔轮,波发生器和钢轮装配;③ 柔轮,波发生器和钢轮装配同时加载负载转矩。分析其在柔轮长轴处的应力和变形,图7为谐波减速器3种装配状态应力云图,图8 为柔轮径向变形量,图9为柔轮齿在长轴处沿轴向变形量。由图8~图9可知,在无转矩的情况下,波发生器装配和钢轮装配使柔轮变形量相近,而转矩的施加使柔轮的变形量产生明显的变化,因此转矩是影响柔轮变形量的重要因素。
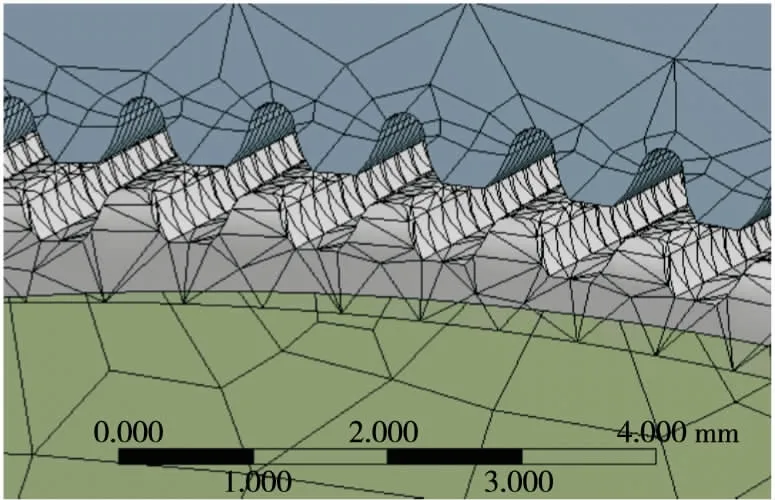
图6 局部网格划分效果图
3 基于响应面模型柔轮应力分析优化
3.1 响应面模型建立
为探究转矩和柔轮齿根圆半径对柔轮应力的影响规律,现建立以转矩和齿根圆半径为参数的响应面模型,探究其对柔轮应力的影响。设计参数分析试验,转矩以两个力Force1和Force2的形式施加在柔轮齿面上,这两个力大小相等方向相反,参数如表2所示。

图7 柔轮齿应力云图
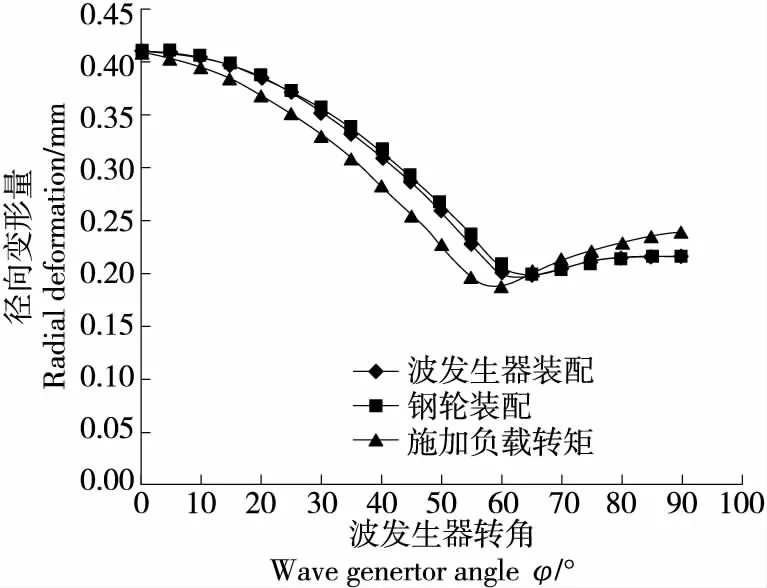
图8 柔轮径向变形量
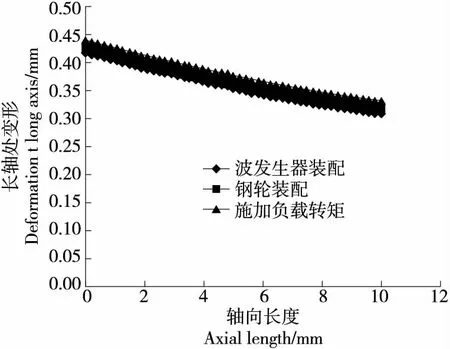
图9 柔轮齿长轴处沿轴向变形量
图10为转矩和柔轮齿根圆半径对柔轮最大等效应力敏感度分析图。由图10可知,转矩对柔轮应力的影响呈正相关,柔轮齿根圆半径对应力的影响呈负相关。而且转矩和柔轮齿根圆半径都对柔轮应力有着较大的影响,所以如何在转矩和柔轮齿根圆半径所选用的取值范围内取得合适的值,使得柔轮的应力最小还需要进一步探究。
3.2 柔轮参数对柔轮应力影响规律
由图11可知,柔轮应力随着负载转矩的增加而增加,随着齿根圆半径的增加而下降。柔轮齿廓参数(柔轮齿根圆半径)对应力的影响比负载转矩更加明显,这是由于谐波传动为多齿啮合传动,单齿所受到的应力较小。当柔轮半径取0.09 mm,负载Force1=100 N时,柔轮等效应力最大;当柔轮半径取0.11 mm,负载Force1=90 N时,柔轮等效应力最小。
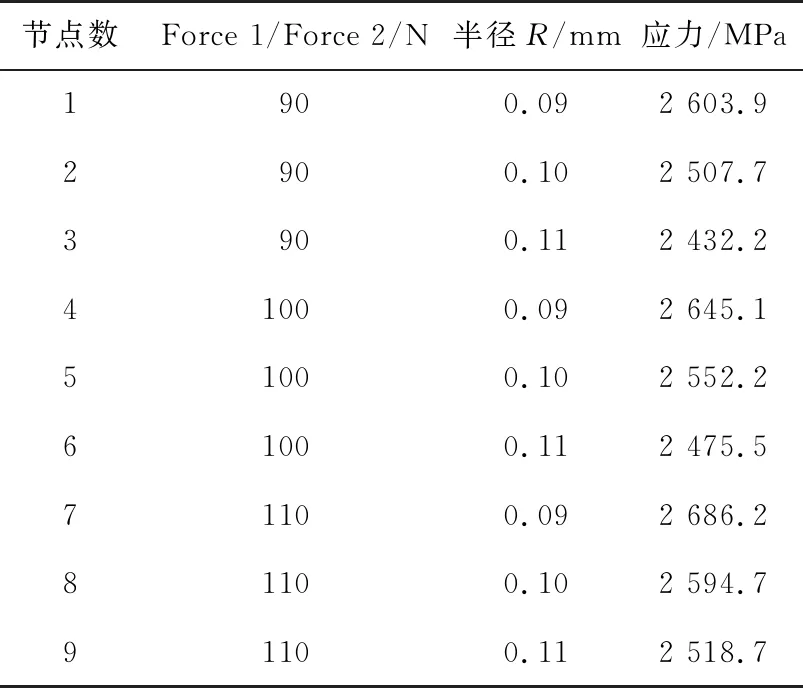
表2 柔轮参数设计点表
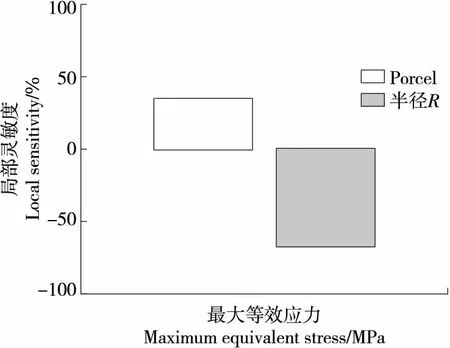
图10 柔轮参数应力敏感度

图11 柔轮参数对应力影响云图
4 结论
(1) 基于包络理论,结合运动仿真的数值解法,是一种可行的求解谐波传动共轭齿廓的方法。
(2) 由柔轮的一个单齿相对于共轭的钢轮齿廓以一个完成的啮入啮出过程画出的运动轨迹,通过调节柔轮的齿形,使其啮合过程在钢轮齿廓的包络下,无干涉发生。当柔轮齿主截面相对于后截面调节角度为β=0.679° 时,柔轮齿轨迹与钢轮齿无干涉发生。
(3) 由于谐波传动为多齿啮合传动,单齿所受的载荷较小,所以柔轮转矩相较于齿廓参数对应力的影响较小。
(4) 试验仅为理论分析,所求共轭齿廓的啮合性能还需进一步验证。
