全数字单载波接收机位同步研究*

孙健兴，汤 韡，张 晶，代 荣

（武汉中原电子集团有限公司，湖北 武汉 430205）

0 引言

位同步也称为定时同步、符号同步、码元同步，是数字通信系统特有的一种同步[1]。传统的位同步方法往往需要通过一个环路控制压控振荡器（Voltage-Controlled Oscillator，VCO）调整接收机的采样时间，进而实现精确的位同步。随着软件无线电技术的发展和基带数字芯片处理能力的提升，出现了全数字位同步技术[2]。如图1所示，接收机以一个自由运行的时钟进行采样，需要位同步的所有操作均在数字域完成，简化了外围模拟电路设计，便于实现算法的优化升级。

图1 全数字位同步结构

根据位同步算法控制方式的不同，位同步可分为反馈式位同步[3]和前馈式位同步[4]。对于连续信号，反馈式位同步的建立时间相对于信号持续时间的占比小，可以比较好地进行同步跟踪，消除建立同步后收发两端晶振偏差累积带来的位同步误差；而对于突发信号，信号持续时间较短，要求位同步建立时间尽可能短，因此常采用前馈式位同步算法[5]。

针对短时间突发传输的单载波系统，本文给出了一种前馈式的全数字位同步算法。该算法在完成初始同步后，利用物理帧头的伪随机序列信息直接估算最佳采样时间，通过插值算法恢复出最佳采样时间的采样值，从而在不增加其他冗余信息的条件下，实现了位同步算法的快速收敛。

1 位同步算法设计

1.1 单载波接收机系统模型

图2为本文考虑的单载波系统接收框图。其中，位同步算法包括初始同步和精同步两部分。初始同步与信号的达到检测同时完成，即通过检测信号到来时接收相关器产生的相关峰位置获得位同步定时的初始估计。由于信道传输延时和收发两端时钟相位的偏移，接收端采集的样点可能没有所需的最佳采样值。通过插值算法可计算出接收信号最佳采样时刻的值，从而实现接收信号的位定时恢复。图2中未对位同步后的接收机解调模块作特别限定，即本文位同步算法不依赖于其他解调模块，可适用于单载波频域均衡、多进制扩频等多种单载波系统。

图2 单载波接收机

1.2 初始同步

Schmidl等人提出的对接收信号进行滑动窗口自相关计算，利用帧结构设计中两段连续的相同序列产生的相关峰，可以获得初始位同步估计[6]。Schmidl方法最初应用于OFDM多载波系统，优点是运算量较小，易于实现，但是产生的相关峰最大值的位置在低信噪比和多径条件下会存在不确定性，影响位同步性能[7]。

本文通过对接收信号与本地预存PN序列计算互相关的方法进行初始同步，对接收信号采样点计算相关值r(d)和窗口能量值e(d)：

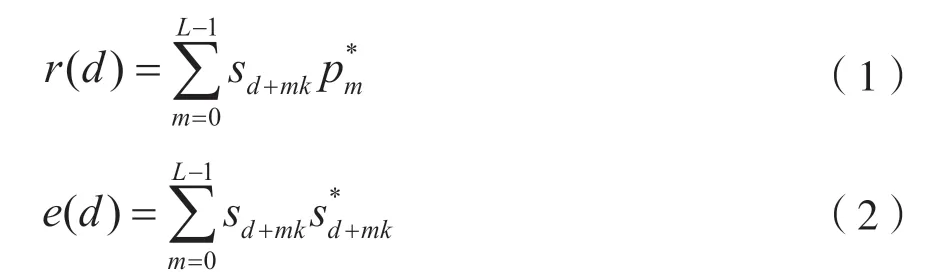
式中，d是采样点标号，L是PN序列长度，sd表示第d个采样的值，p是本地预存的PN序列，k是接收机采样倍数。假设符号时间长度为T，采样时间间隔为Ts，有：

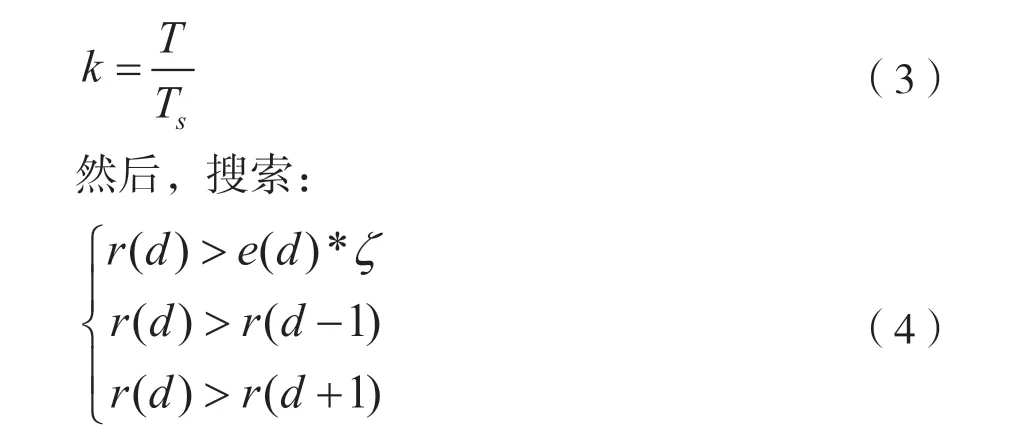
式中，ζ是一个常系数。

图3和图4分别是理想信道下和多径信道下Schmidl方法和本文方法计算获得的相关峰对比。可以看出，本文方法计算产生的相关峰相比于Schmidl方法更加陡峭。在多径信道下，Schmidl方法产生的相关峰出现了展宽，而本文方法保持了良好性能，且准确指示了3条多径的起始位置，对实现一些均衡算法（如Rake接收机）具有实际意义。

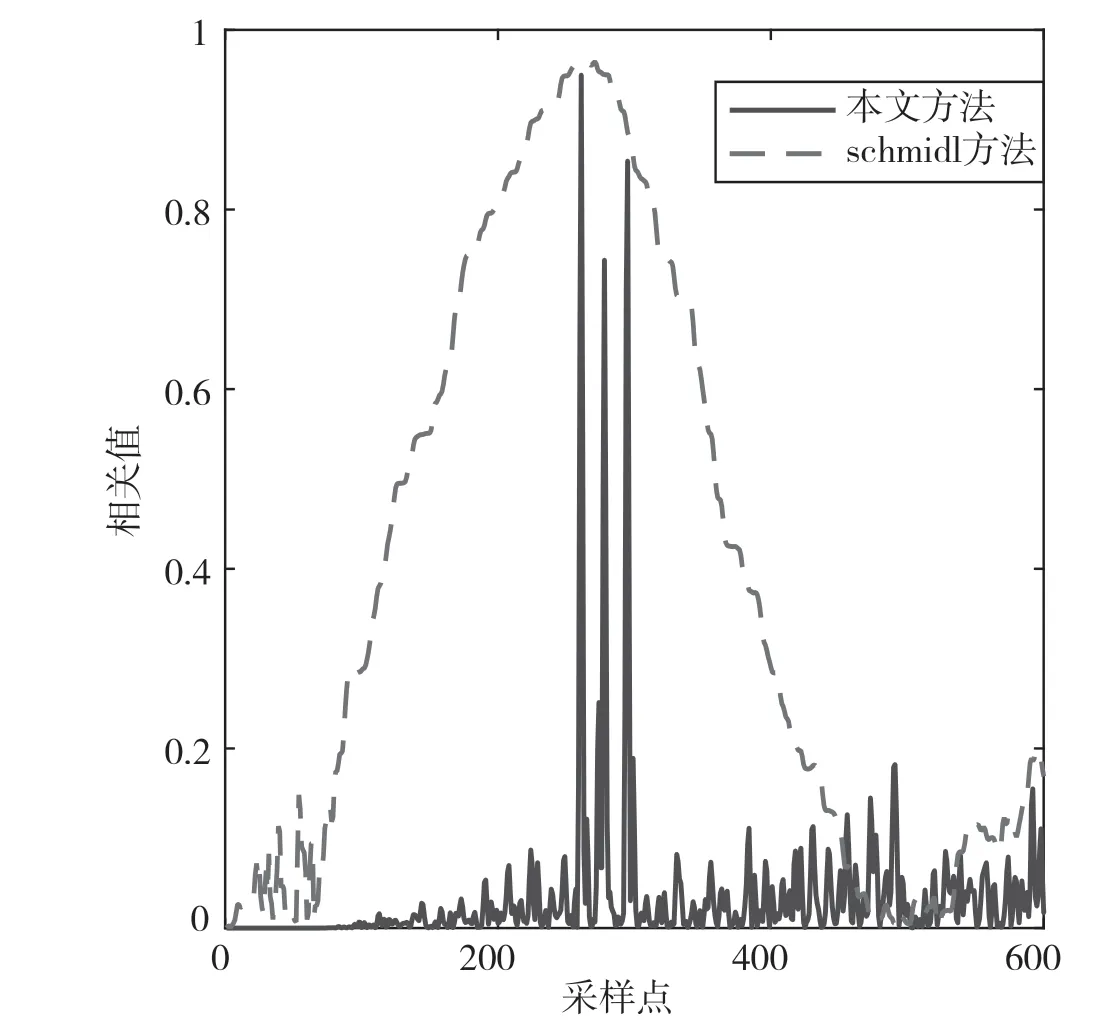
图4 三径信道下相关峰

1.3 精同步

反馈式位同步通常采用Farrow结构[8]的插值滤波器进行。该方法需要不断对接收符号提取定时误差，经过环路滤波后送数控振荡器（Numerically Controlled Oscillator，NCO）产生下一内插时刻[9]。反馈式位同步算法的收敛时间很大程度上取决于提取定时误差的精度，而定时误差的计算精度又是由接收信号的信噪比决定的。因此，反馈式位同步算法的收敛时间存在一定的不确定性，不适用于突发传输。

本文主要考虑突发传输，且一个数据帧的持续时间很短，可以认为建立同步后收发两端的晶振偏差累积不会导致一帧时间内位同步最佳采样位置发生改变。所以，可以在完成初始同步后进行一次最佳采样位置估计，后续不再作同步跟踪调整。

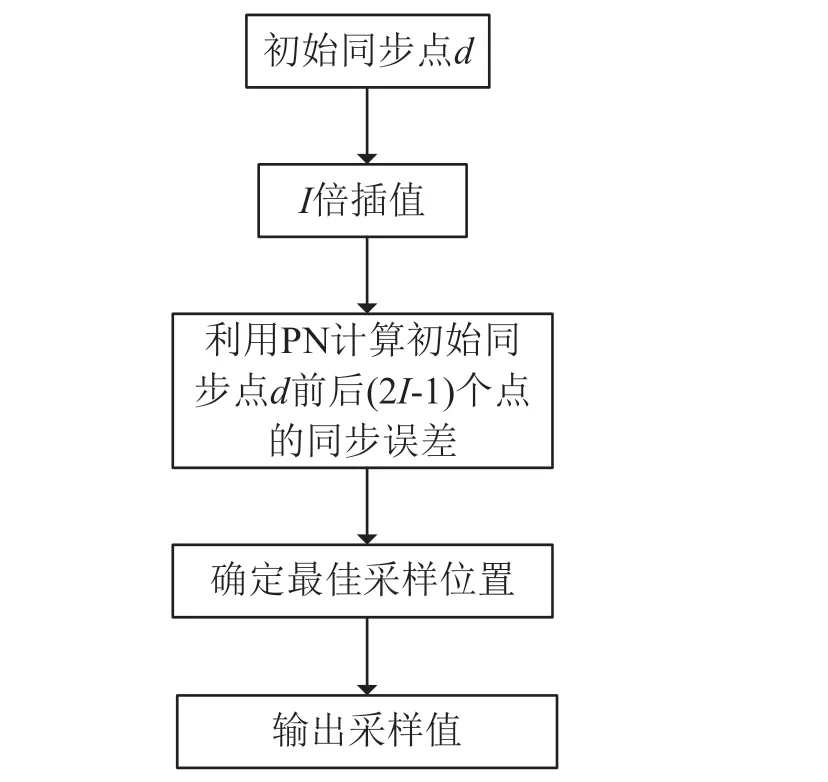
图5 精同步流程

不同于Gardner从未知符号中提取同步误差，本文根据已知的物理帧头PN序列提取位同步误差。在获取初始位同步采样点d后，对接收信号进行I倍内插，对内插得到的高倍采样信号从(d-I+1)时刻开始计算(2I-1)个定时误差值ε：

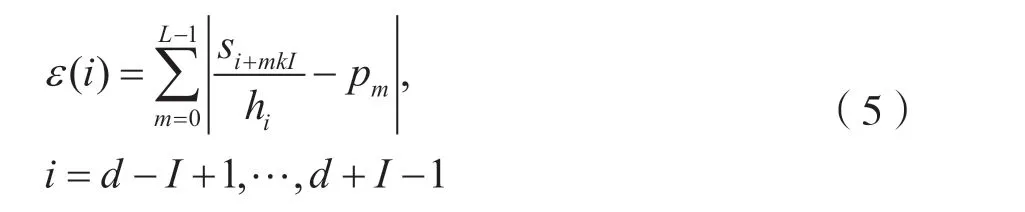
式中，i是插值后信号的采样点标号，hi是信道参量，有：

于是，可得前导PN序列第一个码元的最佳采样时刻的isample为：

相应地，后续各个码元的最佳采样时刻为isample+kI，isample+2kI……

在进行信号插值时，可以采用线性插值或拉格朗日多项式插值[10]。图6给出了插值倍数I=4时，对16QAM调制信号的同相分量分别采用线性插值和多项式插值恢复原信号的情况。可以看出，多项式插值时恢复的信号更接近于原信号，因为经过滤波的16QAM信号本身更加接近于高次多项式曲线特性。

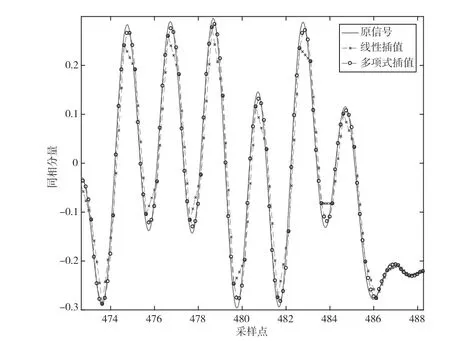
图6 线性插值与多项式插值

图7给出了当收发两端采样时钟相位存在偏差时，在不同信噪比条件下初始同步、线性插值精同步和多项式插值精同步后采样获得的星座图。可以看出：（1）即使在很高的信噪比条件下，仅仅依靠初始同步也无法获得清晰、可解调的星座图，因为每个经过成型滤波和匹配滤波后的接收符号波形只有在最佳采样时间是无失真的，其他时间的波形都包含了其前后符号波形的叠加，即产生了码间串扰；（2）在高信噪比条件下，多项式插值获得的星座点位比线性插值更加聚拢，显示出一定优势，但随着信噪比的降低，这种优势逐渐降低。

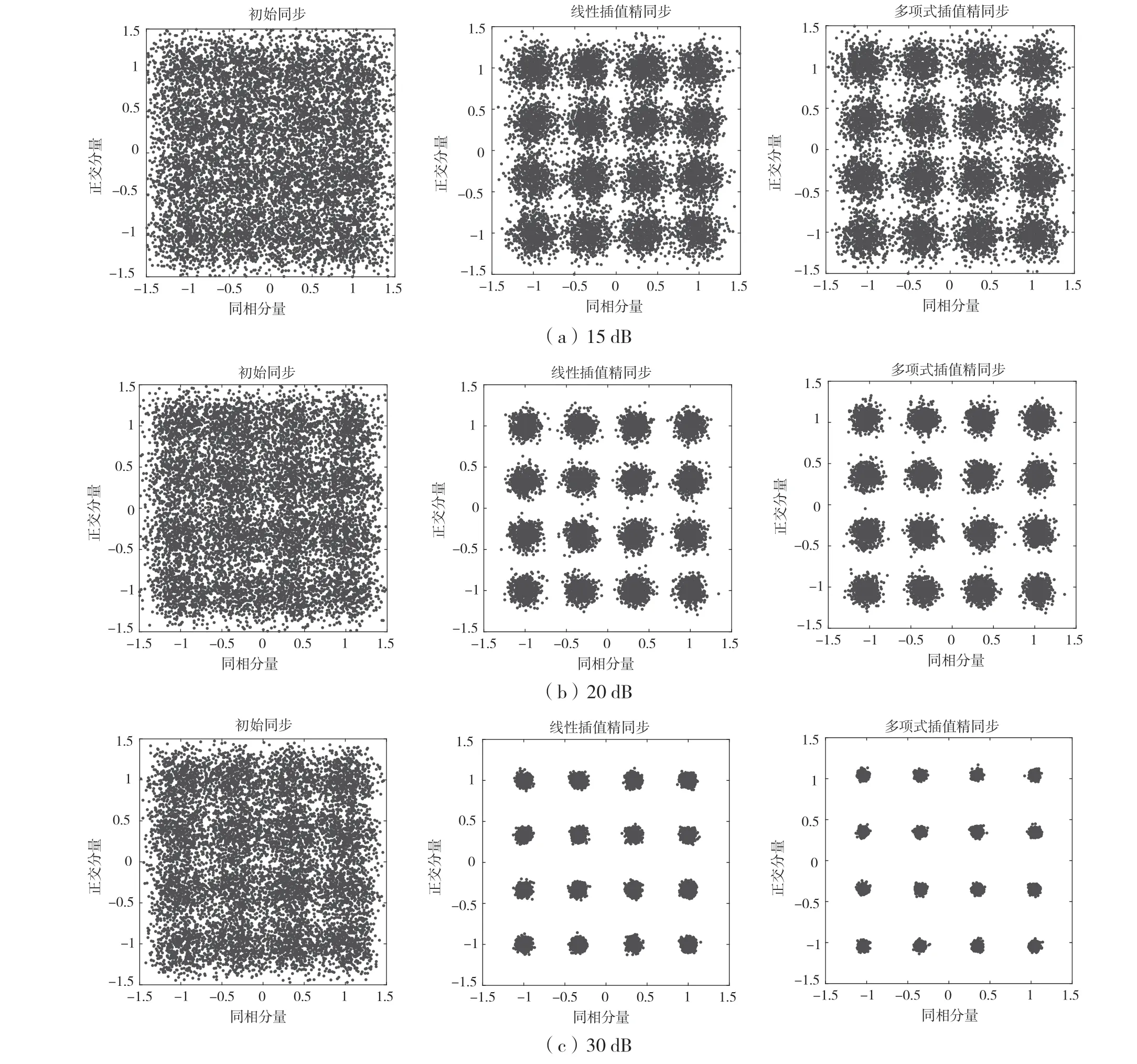
图7 位同步后星座图

2 系统仿真

2.1 仿真环境与参数

本文采用Matlab进行数值仿真，具体仿真参数如表1所示。

表1 位同步仿真参数

2.2 仿真结果与分析

图8为分别采用Schmidl方法和本文方法，在AWGN信道下统计初始同步定时估计样点的绝对误差的均值和方差。可以看出，在SNR＜15 dB时，Schmidl方法的初始同步性能较差，而本文方法的同步误差均值始终保持在0附近。在高信噪比条件下，Schmidl方法仍会存在少量的同步误差。本文采用前馈式的精同步算法，只在初始同步后计算一次最佳采样时刻而不进行跟踪调整。初始同步的性能对精同步影响很大，因此Schmidl方法不适用于本文的精同步算法。

图9和图10分别给出了在AWGN信道下接收机2倍采样和3倍采样时，采用线性插值和多项式插值进行位同步的误码率仿真曲线。接收机2倍采样时，多项式插值相对于线性插值误码率性能有比较明显的优势。以误码率达到10-6为解调门限，拉格朗日插值相对于理想16QAM性能大约恶化了1.8 dB。接收机3倍采样时，线性插值和多项式的误码率曲线几乎重合。因此，在实际工程实现时，若接收机采样率较低，可采用拉格朗日插值提高性能；若接收机采样率较高，可采用线性插值降低实现复杂度。

图8 初始同步绝对误差均值与方差

图9 接收机2倍采样误码率曲线

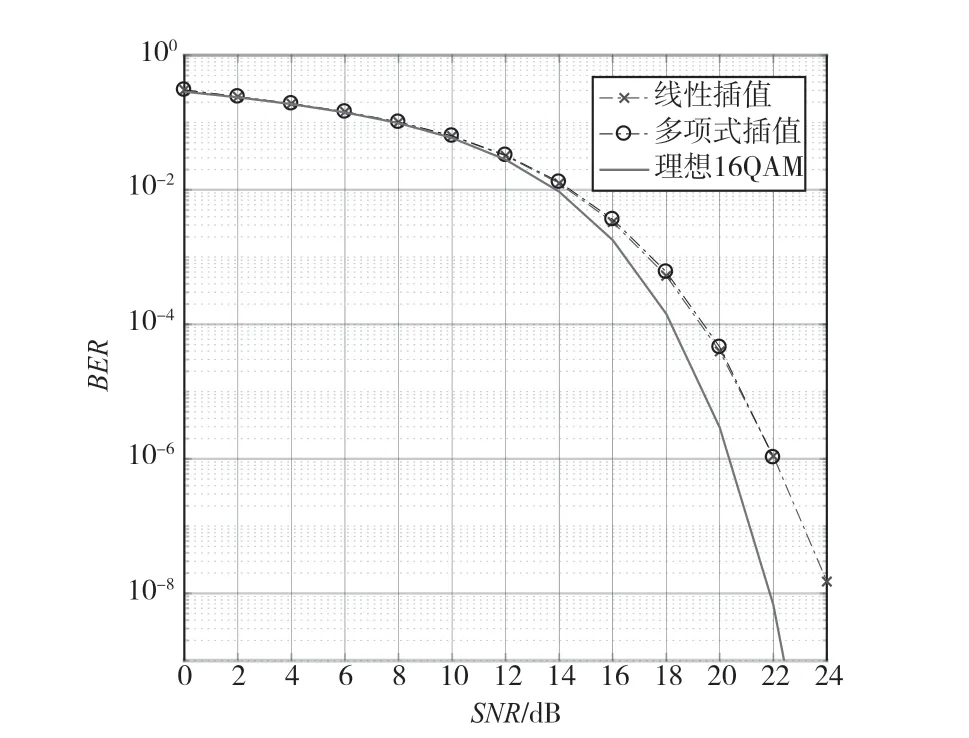
图10 接收机3倍采样误码率曲线

3 结语

随着单载波频域均衡、多进制扩频等技术的发展，单载波系统在未来宽带无线通信领域有着越来越广阔的应用。因此，针对单载波突发传输，给出了一种全数字前馈式位同步算法。该算法在完成初始同步后，利用物理帧头的伪随机序列信息直接估算最佳采样时间，并通过插值算法恢复出最佳采样时间的采样值，从而在不增加其他冗余信息的条件下，实现了位同步算法的快速收敛。计算机仿真结果表明，本文算法可有效解决全数字单载波接收机采样时间不理想引起的码间串扰问题，且对不同采样率的接收机可采用不同的插值算法，以达到接收性能与处理复杂度之间的均衡。