一种高动态长伪码信号的捕获方法*

李 程

（中国电子科技集团公司第五十四研究所，河北 石家庄 050081）

关键字：PMF-FFT；折叠匹配滤波器；高动态；长伪码捕获

0 引言

卫星通信以其全天候、广地域和高灵活性在军民领域中均得以广泛的应用。但是卫星通信系统链路环境较为复杂多变，特别是在高动态条件下，链路上的多普勒频移导致信号的捕获和跟踪难度较大，这也一直是工程研究的热点和难点。在低速通信中，常结合扩频通信整体设计，这样可以提升其抗干扰能力和高可靠性，降低实现难度。目前扩频通信中较为成熟的捕获算法有滑动相关算法、匹配滤波算法以及基于FFT的捕获算法等，部分匹配滤波-快速傅立叶变换（Partial Match Filter Fast Fourier Transform，PMF-FFT）是最近研究的热点，主要用于捕获高动态长伪码信号，其捕获用时较短、捕获频偏范围较宽。PMF-FFT算法多用FPGA实现，对逻辑资源和RAM资源消耗量也较大，特别是当扩频信号的伪码长度较长或多普勒频偏过大时，会导致硬件资源占用过多而不可实现。本文论述一种PMF-FFT实现方法，通过非相干累积和匹配滤波器组的折叠，优化了资源使用率，实现了高动态长伪码信号的捕获。通过仿真和测试，捕获概率为99%时，捕获时间小于1 s。

1 PMF-FFT算法分析

假设信号码长为N，多普勒频差为∆f，码宽为Tc，若对此信号实现捕获，此时的归一化相关输出值为[1]：

式中，r(k)为接收信号；c(k-n)为本地伪码；∆(φ)为接收相差。

当r(k)与c(k-n)对齐时，∆(φ)=0，r(k)c(k-n)=1，则式（1）可表示为：

部分匹配滤波算法是将式（2）中长为N的匹配滤波器分成K段长为M的部分匹配滤波器（N=K×M）,可得出：

对K段部分匹配滤波器输出的相关值进行K点FFT运算，输出结果中第k点的归一化幅频响应为：

若k点FFT结果取模之后的峰值大于判决门限，则捕获成功，FFT估计的载波频差为接收端需要补偿的频差值[2]。对固定的∆f，比较这K个GPMF-FFT(k,∆f)的函数值，可得捕获的相关增益A(∆f)。

若扩频信号信息速率Rb为1 kb/s，扩频周期N为1 024，采样因子K为2，M为128，则码片速率Rc=1.024 Mb/s，码片周期Tc=1/Rc，部分匹配滤波器级数X=KN/M=16，则在伪码同步时，PMF-FFT算法的相关增益如图1所示。

捕获输出的归一化增益在0～8 kHz范围内并没有随着频偏的增加而急剧下降，在系统频偏过大时，PMF-FFT算法不会因为相关增益过低导致相位漏检，即系统的频偏搜索范围变大。由此可得，PMF-FFT算法能够解决大频偏问题。

在PMF-FFT捕获算法中，部分匹配滤波器的长度需慎重考虑，不可过大或过小[3]。部分匹配滤波器的长度过大会导致捕获带宽变窄，长度过小会导致FFT点数过多，导致FFT计算量过大，资源占用和计算延时增加，因此须合理平衡匹配滤波器的长度和FFT点数。由式（5）可知，接收信号与本地伪码的相关增益会受到部分匹配滤波器的频率响应GPMF(k,∆f)的影响。当频偏很大时，相关增益衰减十分明显。图2是M=64，32阶滤波器时PMFFFT输出的相关增益。

从图2可知，基于PMF-FFT的捕获算法对频偏的搜索范围是有限的。因此在进行匹配滤波器长度设计时，要合理计算频偏搜索范围，同时保证正常捕获。

算法处理流程如图3所示。信号Rx经过预处理产生I、Q两路信号，送入匹配滤波器组进行相关运算，每个滤波器组由相关器和M阶累加器组成，I、Q两路数据先相关再累加生成n个数据，将累加结果送入N（N≥n）点FFT模块进行运算，将输出结果与预设门限进行判决，若输出结果高于门限，则表示成功捕获[4]，通过捕获的相位位置计算可得出系统频差。

图1 PMF-FFT捕获算法输出增益

图2 PMF-FFT输出增益

图3 算法处理流程

本文中扩频信号伪码长度为40 800，码速率为2.5 Mc/s，频偏范围为±20 kHz。如图4所示，经过仿真计算，若需捕获概率大于99%，部分匹配滤波器长度为256，FFT点数为256。

图4 基于PMF-FFT的捕获仿真结果

下面给出具体的实现方法。

2 算法实现

2.1 PMF部分实现

常规方法的部分匹配滤波器实现过程如图5所示，处理过程需要L级数据寄存器、L级相关寄存器和K级累加寄存器。

部分匹配滤波器长度为256，FFT计算点数为256点，需要缓存的点数为256×256=65 536点，按照输入数据2 bit量化，2倍采样计算，若使用常规的PMF-FFT算法，其数据寄存器和相关寄存器使用量为524 288 bit。以Xilinx的XC7VX690T型号FPGA为例，其逻辑资源为693 120，已经占据其75%的逻辑资源，综合资源使用情况，难以实现算法。

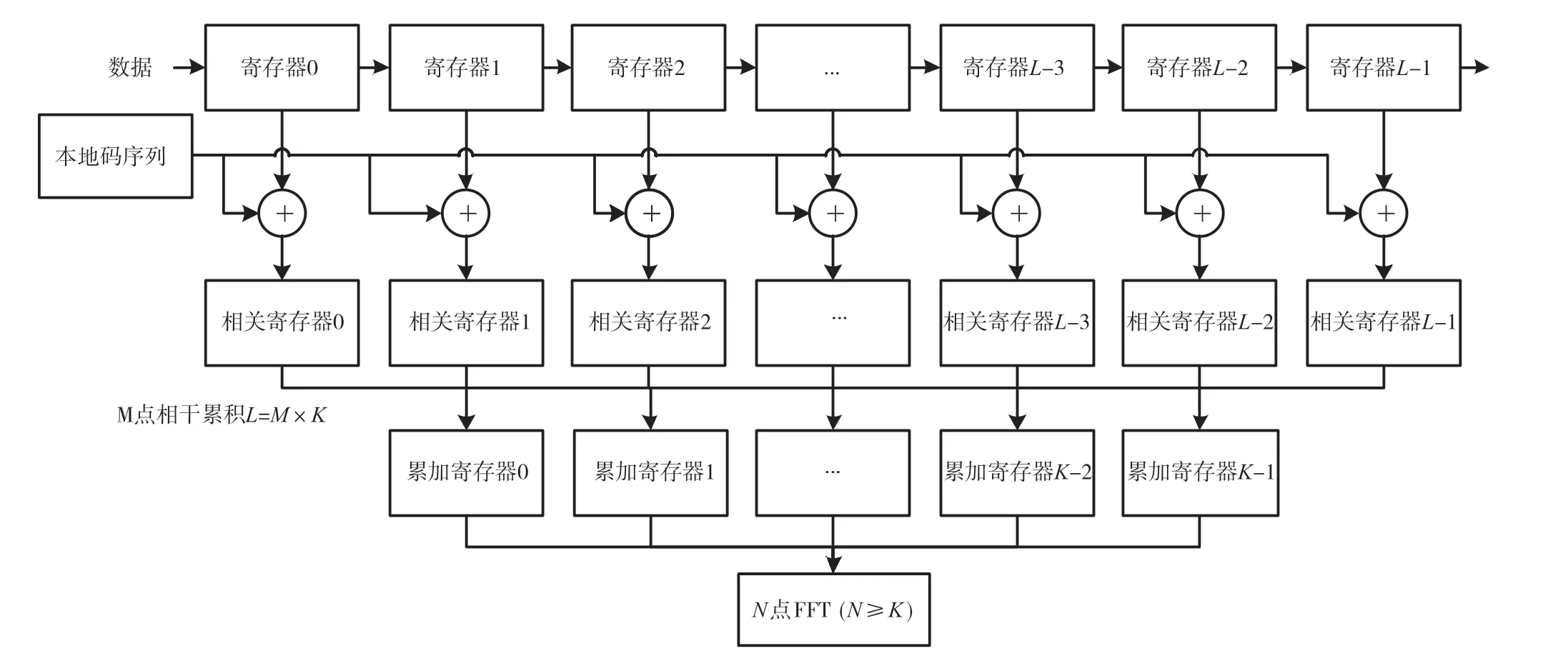
图5 常规PMF实现流程

本文参考一种折叠匹配滤波器[5]，如图6所示，通过RAM资源与逻辑资源的优化互换，将待运算数据和码字序列缓存于RAM中，将匹配滤波器组折叠，使用流水线思想，多级复用，使用高速时钟处理低速数据，减少了近一半寄存器的使用。具体实现流程如图7所示。

图6 基于RAM的折叠匹配滤波器实现流程

图7 RAM存取数据流程

例化8个宽度为512，深度为32的RAM，用于存储输入数据。在码周期开始后，RAM地址由0开始，累加至31，每次读出的数据既要用于相关运算，还需要将其低510 bit与上一地址高2 bit（0地址为输入数据）拼接，再次写入本地址中。实现在每个码周期读一次数据，更新一次数据。

例化8个宽度为256，深度为32的ROM用于存储折叠的伪码序列，ROM地址操作与RAM一致。地址变换的同时，ROM输出本地伪码与RAM输出的缓存数据进行一次相关运算，将结果放入寄存器中进入流水线处理。由于延时固定，流水线会在不同时刻输出对应点的累加结果，将其缓存后给FFT模块使用，如图8所示。

单倍采样的码时钟为2.5 Mc/s，工作时钟为150 MHz，倍数相差60倍。此种折叠匹配滤波器进行了32级折叠，考虑RAM读写和流水线处理延时，足以在60个时钟周期内完成一次PMF运算。

2.2 FFT部分实现

FFT处理模块需要对部分匹配滤波器输出的256个样点进行运算，由于工作时钟为单倍采样码片钟的60倍，而256点FFT的处理延时约为600个时钟周期，因此需要多路FFT并行处理，采用10个FFT模块同时工作，处理流程框图如图9所示。

经过累加输出的256样点数据通过寄存器进行缓存，通过数据选择器依次输入FFT模块进行运算，对FFT输出的数据取模值后与门限进行判决，当模值的峰值高于门限时，则成功捕获，此时FFT峰值点位置的归一化频偏则为载波频差，本算法载波频差估计的范围为：

即捕获频偏范围为±4.88 kHz，分辨精度为：

即经过频差补偿后残留的频差最大值为38 Hz。

针对捕获算法需要满足初始高动态频偏的方案设计如下：频偏范围-20～20 kHz，采用4路并行工作的方法，每个伪码初始位置时进行一次捕获，为实现可靠捕获，进行3次捕获运算，捕获概率大于99.999 9%，最长捕获时间小于1 s。

图8 PMF模块处理流程

图9 FFT模块处理流程

3 结语

PMF-FFT算法广泛运用于高动态长伪码扩频信号的捕获中，但是其资源占用量也相对较多。本文简要分析了PMF-FFT的算法原理，从工程应用的角度阐述了一种优化的PMF-FFT实现方法，通过对部分匹配滤波器组长度的折叠，有效减少了对芯片逻辑资源的使用。本方法已经在工程项目中应用，性能良好，工作稳定可靠。