二元Barycentric-Newton混合有理插值

李 霜，陈豫眉

(1.西华师范大学数学与信息学院，四川南充 637009；2.西华师范大学公共数学学院，四川南充 637009； 3.西华师范大学计算方法及应用软件研究所，四川南充 637009)

0 引言

在自然科学和社会科学领域中存在着许多非线性问题，需要寻找便于处理和计算的函数去逼近非线性问题，常用的一种方法是插值法.多项式插值是数值逼近的基础，具有结构简单、构造容易等特点，如:Lagrange插值、Newton插值、Hermite插值等.有理函数作为非线性逼近的典型之一，具有灵活性强、收敛速度快、逼近效果好等优点.连分式因具有很好的递推性质，常用于构造有理插值函数.其中被广泛使用的是基于连分式与多项式插值通过适当嵌套而构造的有理插值函数[1-6].但基于连分式的二元有理插值构造法也存在着缺点：计算量大，次数高，无法避免极点，数值稳定性不好等.1984年，C.Schneider和W.Werner基于更高次的有理插值函数首次提出了重心插值[7]，其计算量小，且可避免极点，克服了连分式插值的部分缺点.M.S.Floater 和 K.Hormann运用混合函数的插值方法构造了广义重心有理插值[8]

(1)

其中

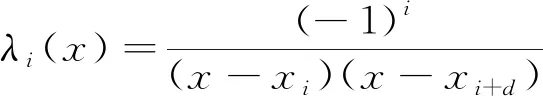
hi(x)(i=0,1,…,n-d)为过插值点xi,xi+1,…,xi+d且次数不超过d的多项式.对(1)式分子分母同乘(-1)n-d(x-x0)…(x-xn)，则(1)式为：

其中

这种广义重心有理插值能有效地避免产生极点，较之重心插值有更高的逼近精度且逼近速度更快.文献[9-10]分别基于重心有理插值与连分式、重心有理插值与Newton多项式，构造了二元有理插值格式.文献[11]基于重心有理插值与两类连分式构造了有理插值格式.文献[12]基于广义重心有理插值与连分式构造了有理插值函数，在此基础上，文献[13]将广义重心插值与连分式、Newton多项式结合，构造了二元混合有理插值格式.本文将广义重心有理插值与Newton多项式相结合，构造出一种新的混合有理插值，该方法继承了广义重心有理插值与多项式的优点.

1 二元Barycentric-Newton混合有理插值

给定矩形网格点

和函数值f(xi,yj)，构造如下格式的二元有理插值函数：

(2)

任意选定整数d，0dm,其中

(3)

(4)

(5)

为满足插值条件r(xs,yt)=f(xs,yt),(s=0,1,…,m;t=0,1,…,n),引入以下偏逆差商.

定义1

(6)

(7)

(8)

称(6)式-(8)式确定的φ[xp,…xq;yr,…,ys]为f(x,y)在给定矩形网格上的偏逆差商.

定理1对s=0,1,…,m;t=0,1,…n，令

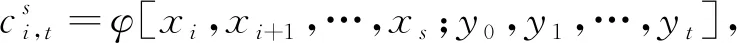
则由(2)式定义的r(x,y)满足插值条件

r(xs,yt)=f(xs,yt),(s=0,1,…,m;t=0,1,…,n).

证明由(5)式可得：

=φ[xi,…,xs;y0]+(yt-y0)φ[xi,…,xs;y0,y1]+…+(yt-y0)…(yt-yt-1)φ[xi,…,xs;y0,y1,…,yt]

=φ[xi,…,xs;y0]+(yt-y0)φ[xi,…,xs;y0,y1]+…+(yt-y0)…(yt-yt-2)φ[xi,…,xs;y0,…,yt-2,yt]

=φ[xi,…,xs;y0]+(yt-y0)φ[xi,…,xs;y0,yt]=φ[xi,…,xs;yt]

记

I={0,1,…,n-d},J={i∈I|s-dis}

由(3)式可知: 当i∈I/J,ui(xs)=0,当s-did，有

2 误差估计

f(x,y)∈C(m+n+2)，有

其中

证明设E(x,y)=f(x,y)Qm,n(x,y)-Pm,n(x,y)，由r(xi,yj)=f(xi,yj)得

E(xi,yj)=0,(i=0,1,…,m;j=0,1,…,n)

于是

E[x0,…,xi;y0,…,yj]=0,(i=0,1,…,m;j=0,1,…n.)

其中E[x0,…,xi;y0,…,yj](i=0,1,…,m;j=0,1,…n.)表示E(x,y)在定义的矩形网格上的Newton差商.

将E(x,y)用Newton插值公式展开可得

从而

3 数值算例

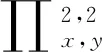
(i,j=0,1,2).

解利用逆差商的递推算法(6)-(8)式，列表计算见表2-表5：

表2 计算结果Tab.2 The calculation results

表3 计算结果Tab .3 The calculation results

表4 计算结果Tab.4 The calculation results

表5 计算结果Tab.5 The calculation results

由(5)式得：

u0(x)=x2-x=2-x,u1(x)=x-x0=x.

由(2)式可得

从而

容易验证r(x,y)满足所给的插值条件.

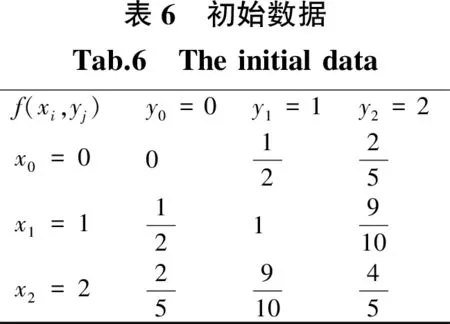
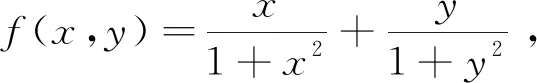
采用本文的方法得到的插值函数为

分别绘制f(x,y),R(x,y),r(x,y)的图像，见图1-图3.

图1 原函数f(x,y)Fig.1 The function f(x,y)图2 插值函数R(x,y)Fig.2 The interpolation function R(x,y)图3 插值函数r(x,y)Fig.3 The interpolationfunction r(x,y)

从图1-图3可以看出，本文方法得到的插值函数r(x,y)光滑性好，无奇异点，比R(x,y)逼近速度更快，逼近的精度更高,可见此算法的正确性与高效性.