Ku频段卫星通信信号自适应检测算法*
2021-05-08李成,白园,陈飞
李 成,白 园,陈 飞
(中国电子科技集团公司第三十研究所,四川 成都 610041)
0 引言
近年来,卫星通信以其频谱资源丰富、支持宽带信号传输、覆盖广、受地理条件限制小等优点,逐渐在军民领域都占有不可替代的重要地位。随之而来的是卫星通信的需求不断增加,支持的应用不断扩展,不明体制、私有协议的信号增多,新的调制方式出现,在非合作条件下,对宽频段卫星信号的截获与分析带来了极大的挑战。
目前,国内针对卫星信号的检测方法如小波变换法[1]、能量检测法[2]、希尔伯特变换法等能够在给定某些先验知识的前提下实现对卫星信号的检测,然而需要一定的人工介入,不能满足对卫星信号检测自适应和普适性的要求。
本文针对以上问题展开研究,首先对Ku频段卫星电磁频谱特征进行分析,采用改进的周期图法与频域低通滤波的方法对信号频谱进行改善,使其更有利于信号检测。其次,在完成全频段频谱拟合拼接的基础上设计了一种合理的迭代策略,能够完成背景噪声统计与检测门限设定,最终根据信号能量与带宽完成目标信号的检测。
1 Ku频段通信卫星电测频谱分析
工作中发现某典型同步轨道通信卫星Ku频段转发器电磁频谱如图1所示。可以看出,该卫星信号个数较多、带宽范围跨度较大,且集中在同一频段。同时,在非合作接收条件受限情况下,发现某些信号包络的起伏较大,背景噪声变化较大,极易造成信号检测虚警或漏判。故需要采用一定的方法对频谱进行处理,此为提高信号检测成功率的基础。

图1 某卫星信号频谱
2 频谱预处理
2.1 频谱平滑
信号频谱处理首先要进行频谱平滑,比较常见的是周期图谱估计法[3]。它取随机信号x(n)的N点观察数据xN(n)直接进行FFT,得到频谱的估计值xN(ω),平方后再除以N,就得到功率谱的估计值,即p(ω)=|xN(ω)|2/N。考虑到在周期图法中对xN(ω)求平方会大大增加硬件计算时间,故本文对上述周期图法进行改进。该方法的思想是对连续接收信号进行分段处理,即根据实际处理带宽和采样率选取合适的FFT点数,然后在时域上截取相同点数的数据做FFT,进一步得到该段信号的周期图,然后对每段数据处理结果求平均,即得到处理带宽范围内初步平滑的频谱。式(1)~(4)给出该方法的一系列公式。
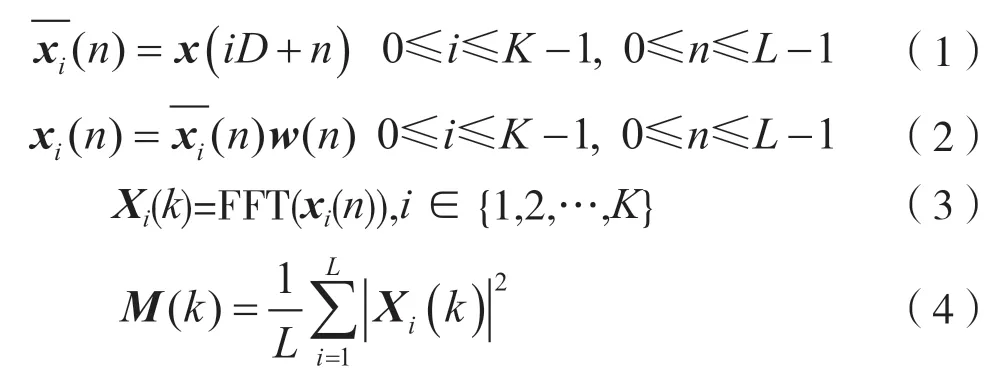
式中,K为连续数据的分段数,每段的FFT点数为L,D指各段数据之间的相对偏移量。
采用本文提出的改进方法,得到功率平均后的频谱,能够大大减小频谱估计的方差。但是当检测时间受限时,一味地增加分段数和数据长度,将不能满足实时处理的需求。因此,要综合考虑处理带宽、采样频率、硬件计算时长等参数,选择合适的数据分段数和每段的数据长度。本文工程中选择将一次处理数据分为20段,每段数据长度为16 384。
图2和图3分别为对某Ku频段卫星实采信号直接进行FFT变换得到的频谱图和采用改进算法得到的频谱图。可以看出,图3信号的频谱明显得到了改善,毛刺也明显减少。
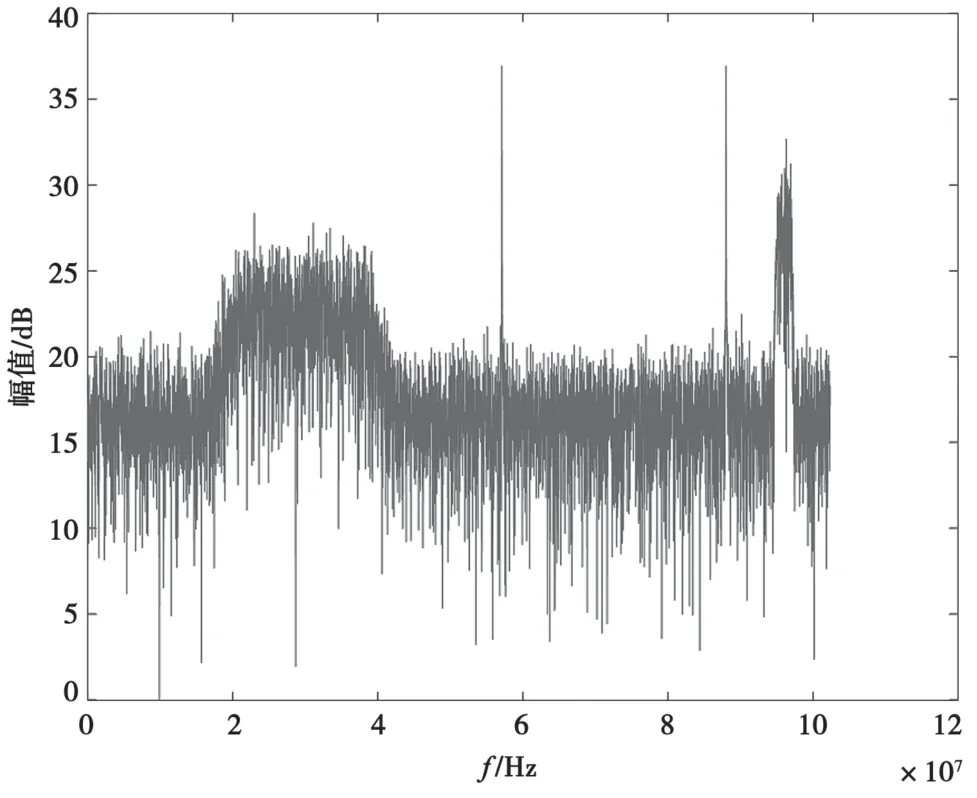
图2 周期图法信号频谱
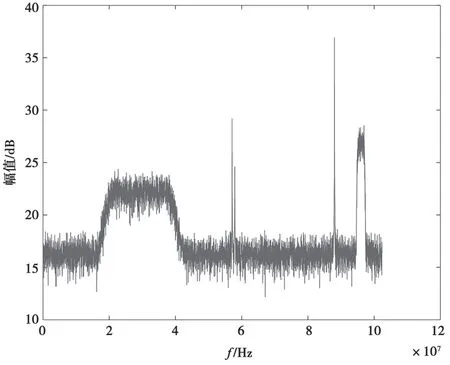
图3 改进的周期图法信号频谱
采用本文方法可使处理带宽范围内信号的频谱变得比较平滑,但是其平滑程度仍然不足以用来做信号的自动检测。借鉴数字图像处理中图像平滑的方法,本文对初步平滑处理后的频谱进行低通滤波,来进一步降低谱估计方差、减少毛刺。
较高阶数的频域低通滤波器能够使信号频谱得到显著的平滑效果,然而过度的平滑意味着“模糊不清”。所以在设计低通滤波器的时候,不能无限制地增加滤波器的阶数,当平滑滤波后的频谱能够比较准确地完成信号自动检测时就够了。另外,由于滤波器的延迟效应,平滑后的频谱会出现“频率右移”的现象,所以应该根据实际情况来确定合理的滤波器参数。本文选用汉宁窗函数,阶数为30阶,采样率为102.4 MHz,通带截止频率为10 kHz,对图3中的频谱进行频域平滑滤波,结果如图4所示。可以看到,平滑滤波器对于连续谱如恒包络的宽带信号有一定的提升效果,对于离散谱如FSK、单音等信号则有一定的降低效果。这种效果对于后续的信号自适应检测非常有利。

图4 频域平滑滤波后的频谱
2.2 基于最小二乘拟合的频谱拼接
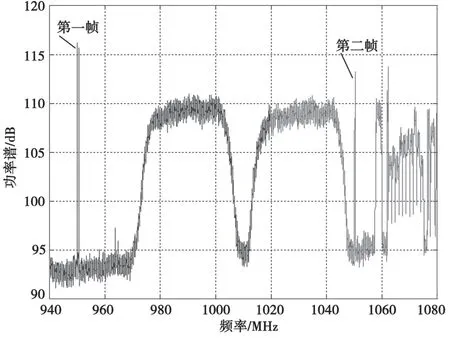
实际应用中通常需要对整个Ku频段(10.95~12.75 GHz)频谱进行计算,以便更准确地估计背景噪声。由于接收设备的带宽限制,每次只能计算一个瞬时带宽内的频谱(称为一帧频谱),故需要多次改变接收频点进行频谱拼接,获得整个频段内的完整频谱。然而每次计算时间存在先后,由于噪底、信号功率等可能的抖动,以及硬件设备(变频、滤波、采集)本身的一致性问题,会导致相邻两次计算出的频谱存在差异,使得拼接后的频谱在前后频点交界位置出现真实中并不存在的能量阶跃或者比例变化,如图5所示。
故可采用如下处理,扫描时让前后帧频谱存在部分重叠,利用重叠部分频谱对后一帧频谱的基准电平、尺度进行估计,补偿后再进行拼接[4]。

图5 原始帧频谱拼接
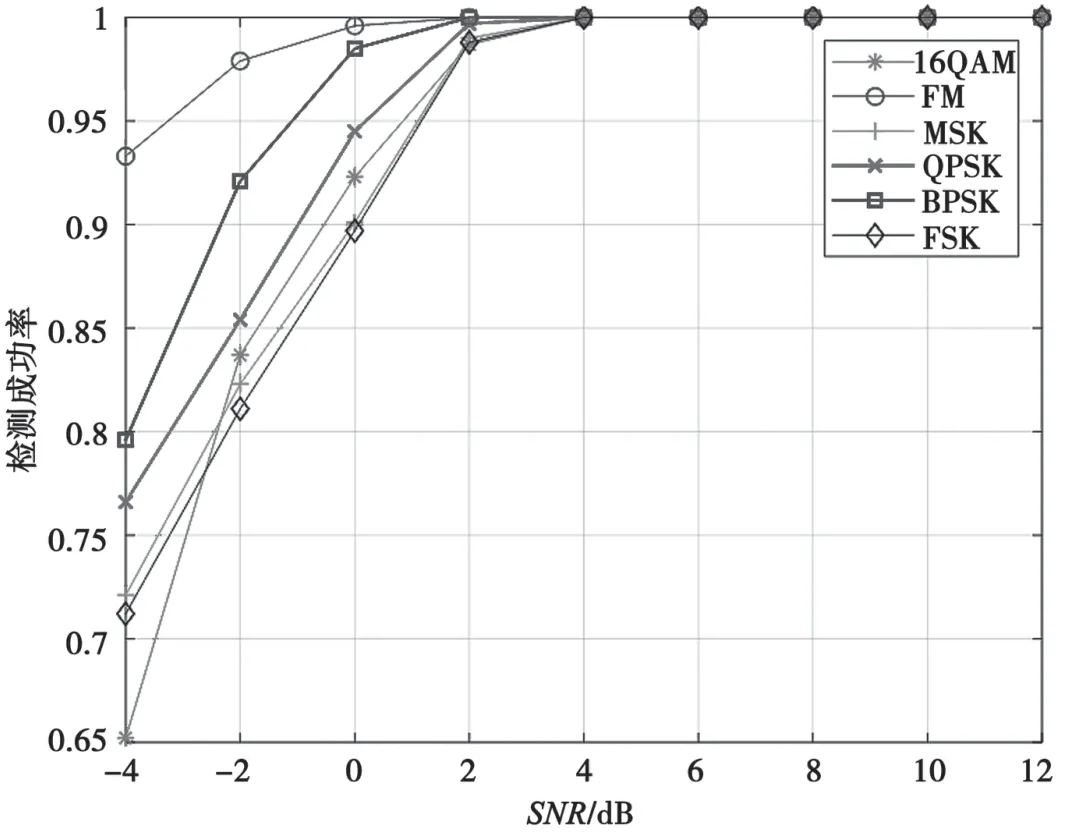
设x1(f),f∈[f1,f3]为第一帧对数频谱,x2(f),f∈[f2,f4]为第二帧对数频谱,其中f1 对式(5)的离散形式,可采用最小二乘方法估计出a、b后,计算补偿后的频谱ax2(f)+b,然后进行拼接。 对图5中的频谱进行拟合拼接,结果如图6所示。 图6 拟合拼接后的频谱 经过改进的周期图法和频域低通滤波处理后的信号频谱底噪起伏非常小,再经拟合拼接,即可在全频段频谱中比较准确地统计背景噪声,并在此基础上设计合适的自适应检测门限。 目前,比较常用的能量检测门限设计准则有以下两种:恒虚警概率准则[5],指要求在保持恒定的虚警概率的条件下,使信号正确检测的概率达到最大值Pf;恒检测率门限准则[6],指能量检测的判决期望对信号检测概率小于或等于一个性能指标Pd。 在实际应用中,由于不同用户发射的信号功率可能不同,不同转发器辐射的EIRP值也可能不同,导致接收不同频段的信号能量不同,恒漏检率和恒虚警率均对判决结果有很大的影响,且根据实际场景的不同,对判决结果的影响也不同。因此,基于以上两种门限设计准则都不太适合本文自适应检测的需求。综合考虑,在先验信息全盲的条件下,为使虚警率和漏检率都尽可能小,对二者加权求和后求最小值,以此作为最优门限设计准则。 采用最优门限准则能达到的错判率门限[7]最小值为: 根据上述最优门限设计准则,本文提出如图7所示的自适应门限迭代策略。 具体流程如下:第1步,求出经平滑处理和拟合拼接后的全频段频谱幅值的平均值,记作Nth1。第2步,基于频谱分辨率,将每个频点对应的谱线幅值与该平均值做比较,幅值小于或等于Nth1的值不变,大于Nth1的将其值改为Nth1。第3步,求出新得到的这一组全频段谱线的平均值Nth2,然后进行和第2步同样的操作,直到前后两次的平均值之差小于一个相对收敛精度(本文采用经验值)为止,可得到比较准确的底噪估计值,将其记为Nth2。在硬件实现时,为了简化算法的复杂度,直接将底噪估计迭代次数最大值定为3次。第4步,根据底噪估值和式(6)计算初始判决门限Vth1。第5步,取第二次全频段谱线重复上述过程,计算新的判决门限Vth2,同样的,直到前后两次的门限值之差小于一个相对收敛精度(同样采用经验值)为止,迭代运算就会收敛,运算终止,得到最终的自适应检测门限。 图7 自适应门限迭代策略 将全频段信号谱线幅值和自适应判决门限Vth做比较,将谱线幅值大于判决门限的点的坐标保存到数组R中。除了特殊体制如PCMA外,卫星信号通常不会在频域混叠。利用每两个信号之间默认存在频率间隔这一点,进行R[i+1]-R[i]计算,如果R[i+1]-R[i]=1,说明这两个谱线幅值是一个信号中频率相邻的两个点。如果R[i+1]-R[i]>1,那么这两个谱线幅值有可能是两个信号起始频率和截止频率分别对应的坐标,但也有可能是较大的噪声毛刺或信号过渡带频谱形状出现凹陷的两个频点对应的坐标。另外,频率间隔设置过大则有可能将两个信号误判为一个信号,故需根据实际频率分辨率来设置频率间隔。本文中设置R[i+1]-R[i]>50,能够使多个信号的检测成功率得到极大提升。 基于上述自适应门限迭代策略,在实际卫星信号检测场景中能够准确检测出多个信号。同时,频率分辨率是已知的,那么可以得到每个信号的起始频率f1和截止频率f2的准确粗估计值。所以信号的中心频率粗估计值fc=(f1+f2)/2,信号的带宽粗估计值B=f2-f1。图8给出自适应检测的流程图。 设置采样率为102.4 MHz,检测频段10.95~12.75 GHz,包含FM、BPSK、QPSK、16QAM、MSK、FSK等6种混合仿真信号。运用本文算法在每个信噪比下进行1 000次蒙特卡洛检测仿真,其检测成功率与信噪比关系如图9所示。 通过仿真发现,本文算法在信噪比大于2 dB时,混合信号的自适应检测成功率几乎可以达到100%,具有较好的性能;迭代次数少且没有大量乘法运算,硬件计算时间较少,易于工程实现;适用于各种调制方式的卫星信号,通用性较好。 图8 自适应检测流程 图9 仿真信号正确检测率与信噪比的关系 本文提出了一种针对Ku频段卫星通信信号的自适应检测方法,能够准确估计全频段底噪,自动设置合适的检测门限,在此基础上得到的信号个数、频点、带宽的粗估计值正确率高。本文算法在设计同时就已经考虑了工程实现的可行性问题,目前该方法已应用于实际工程项目。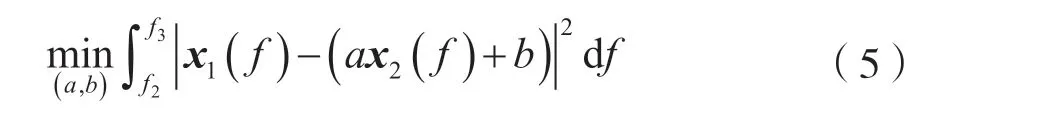
3 自适应检测算法
3.1 底噪估计及门限设置


3.2 多信号自适应检测与粗估计
4 仿真试验及性能分析

5 结语
