关于求解极限的若干思考
2021-05-07林丽琼任立英
周 燕, 林丽琼, 任立英
(福州大学 数学与计算机科学学院,福州350108)
1 引 言
众所周知,无穷小等价替换极大简化了一些极限的求解[1],但在具体应用过程中,细节的错误经常会出现.比如应用无穷小等价替换计算极限时,要求在x0的某个去心邻域里没有零点,很多人在做题过程中往往忽略这一点.
例如错误做法:
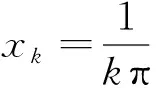
二元函数极限的判别与求解方法众多[2-3],其中应用极坐标计算二元函数的极限是常用的一种方法,但应用时有诸多复杂的限制[4-5],本文针对一类特殊函数给出了便于计算应用的若干结论.
2 主要结果
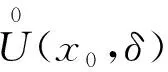
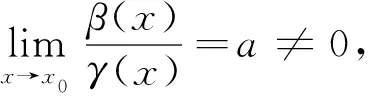
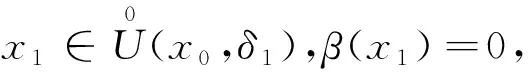
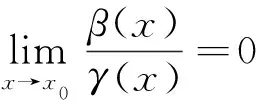
类似地有
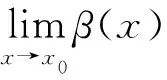
证法同引理1
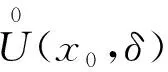
(i) 在E中,β(x)与β1(x)的零点相同,记E1={x∈E|β(x)=0}={x∈E|β1(x)=0};
(ii) 对任意ε>0,存在0<δ2≤δ1, 当0<|x-x0|<δ2,且x∉E1时,有
则
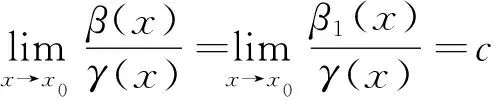
证令
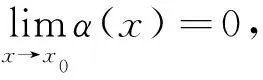
由引理1得
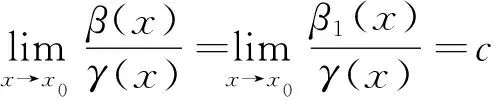
同样,由引理2可得如下类似结论:
定理2设β(x)与β1(x)为x→x0时的无穷小,在x0的任一去心邻域,β(x),β1(x)均有零点,γ(x)在x0的某去心邻域内有定义,若存在x0的某个去心邻域E={x|0<|x-x0|<δ1}满足:
(i) 在E中,β(x)与β1(x)的零点相同,记E1={x∈E|β(x)=0}={x∈E|β1(x)=0};
(ii) 对任意ε>0,存在0<δ2≤δ1, 当0<|x-x0|<δ2,且x∉E1时,有
则
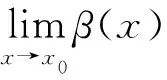
大家知道应用无穷小等价替换计算极限时,要求在x0的某个去心邻域里等价替换的函数没有零点,而定理1则把无穷小等价替换的结论进行了推广,它说明在求解极限时,分子若应用无穷小等价替换时,允许x0任意去心邻域函数都有零点,只要满足两个无穷小在x0的某个邻域内零点相同,并且不考虑零点的时候,表达形式满足通常等价的情况,也即非零点x在充分靠近x0时满足
则计算极限时是可以将β(x)与β1(x)进行替换的.
经常碰到的题目忽略了等价替换的条件,利用等价替换得到的结果都是正确的,原因就在于题目实际上满足定理1的条件.
类似一元函数可以证明对于多元函数上述的引理1、引理2以及定理1、定理2也都成立,这里就不逐一叙述,仅以二元函数的情况为例说明定理1的推广内容.
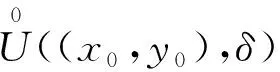
(i) 在E中,β(x,y)与β1(x,y)的零点相同,记
E1={(x,y)∈E|β(x,y)=0}={(x,y)∈E|β1(x,y)=0};
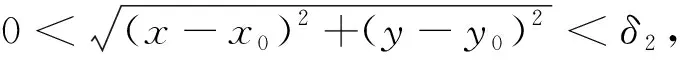
则
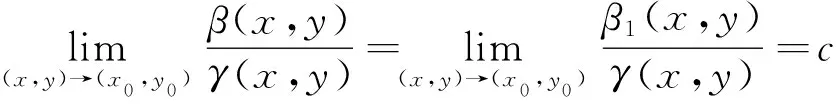
证明与定理1类似,略去.
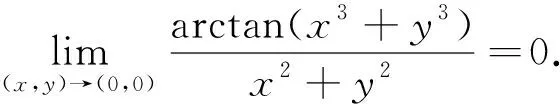
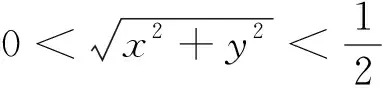
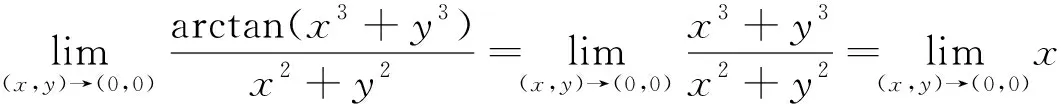
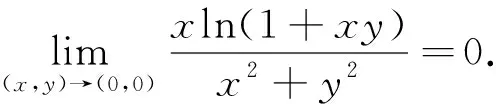
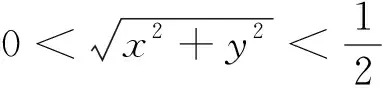
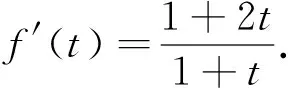
当t>0时,f′(t)>0,所以2t>ln(1+t)>0,
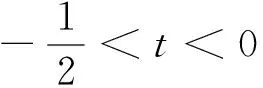
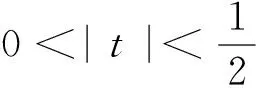
|ln(1+t)|<|2t|.
(1)
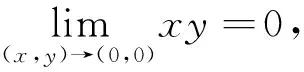
由夹逼准则可得
由上述证明过程可以看出例2若不采用我们证明的定理3,则计算比较麻烦,而且学生不容易想到将ln(1+xy)与2xy进行比较,而选择应用定理3,则计算简单.
总而言之,如果在去心邻域函数出现零点,关键要考虑函数无穷小替换时零点是否可以保持,如果可以,事实上应用本文的结论是可以替换的,而且结果是正确的.这样在计算一元或多元函数极限的问题上方便很多.
下面讨论应用极坐标求解极限时易犯的错误的问题.比如
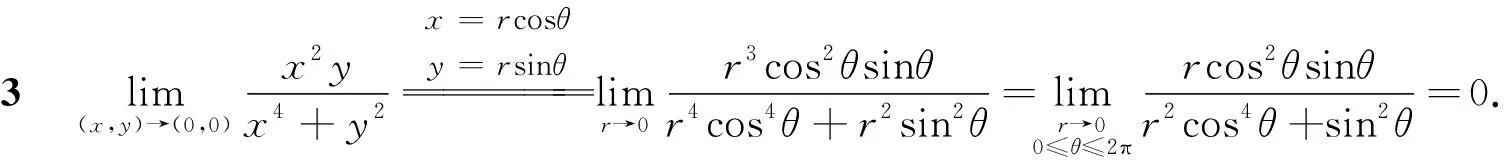
该题应用极坐标替换计算极限过程中,将θ当作是常数,计算r→0时的极限,事实上在r→0的过程中,θ也是变化的,是不能当做常数的,所以计算结果是错误的.事实上,该函数的极限是不存在的.
那么怎么利用极坐标计算的结果是正确的呢?在文献[4-5]中给出的具体的命题如下:
命题1[4]设二元函数f(x,y)在点(x0,y0)的某去心邻域内有定义,则
命题2[5]设(i) 任意θ∈[0,2π],当r→0时f(x,y)=f(rcosθ,rsinθ)→0;
(ii) 存在M>0,使得任意(x1,y1),(x2,y2)有
|f(x1,y1)-f(x2,y2)|≤M(|x1-x2|+|y1-y2|),
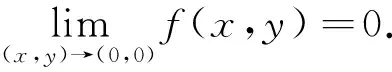
上述结论提到的要求比较复杂,且这些结论在具体计算时并不好验证,本文给出两种适合计算中应用的方法.
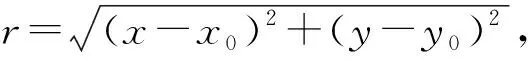

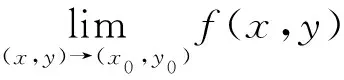
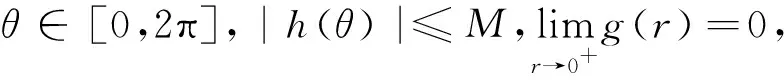
|f(x,y)|=|f(x0+rcosθ,y0+rsinθ)|≤|g(r)h(θ)|<ε,
所以
时,
|f(x,y)-A|=|g(r)h(θ)-A|<1,
故
|g(r)h(θ)| 由于g(r)在0的任一去心右邻域不恒为0,则存在0 这两个结论虽然简单,但在计算二元函数极限时,却是十分方便. 例4若不采用极坐标替换来解决,则计算量会很大.而对于例5,学生往往不太容易看出是极限不存在,而通过上述方法,可以轻松地解决问题. 极限的计算在高等数学中占有重要的地位,本文通过具体例题指出学生在应用等价替换与极坐标变换计算极限时易忽视的错误,并通过严格证明给出修正错误的相应结果,这不仅有助于学生透彻掌握等价替换与极坐标变换求极限的方法,且可避免容易忽视的错误,同时也为教师在教学中提供参考.事实上,在高等数学学习过程中,这类容易忽视的错误经常可见,对这种类似问题的研究对教学与学生学习都有很大帮助. 致谢在论文修改过程中,审稿老师提了许多宝贵意见,对此表示衷心的感谢.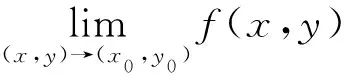
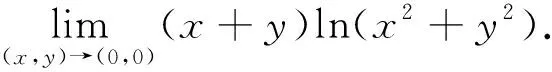
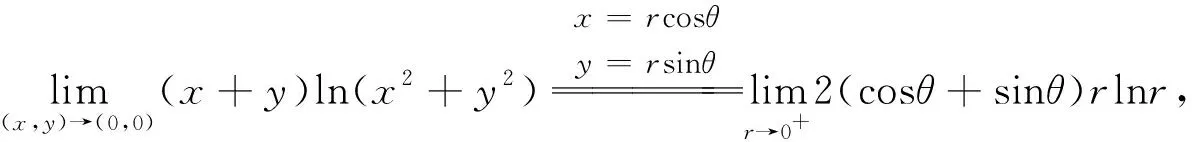
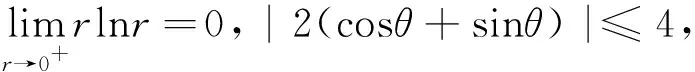
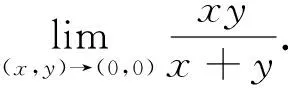
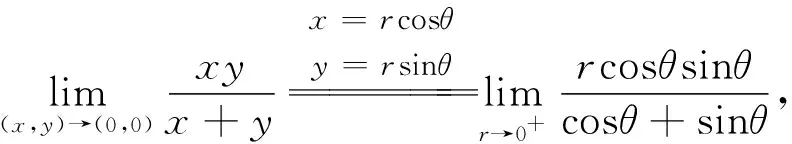
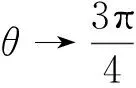
3 结 论
