基于球坐标计算第一型曲面积分注记
2021-05-07曲智林
潘 宁, 曲智林
(东北林业大学 理学院,哈尔滨150040)
1 引 言
在高等数学或数学分析教材中,关于第一型曲面积分的计算都是在直角坐标系下进行的,例如设空间曲面S的方程为
z=z(x,y), (x,y)∈σxy,
其中σxy为曲面S在xOy平面上的投影域,且z(x,y)具有一阶连续偏导数,见图1.函数f(x,y,z)在曲面S上连续,则对面积的曲面积分(第一型曲面积分)可化为二重积分计算[1-2]
(1)
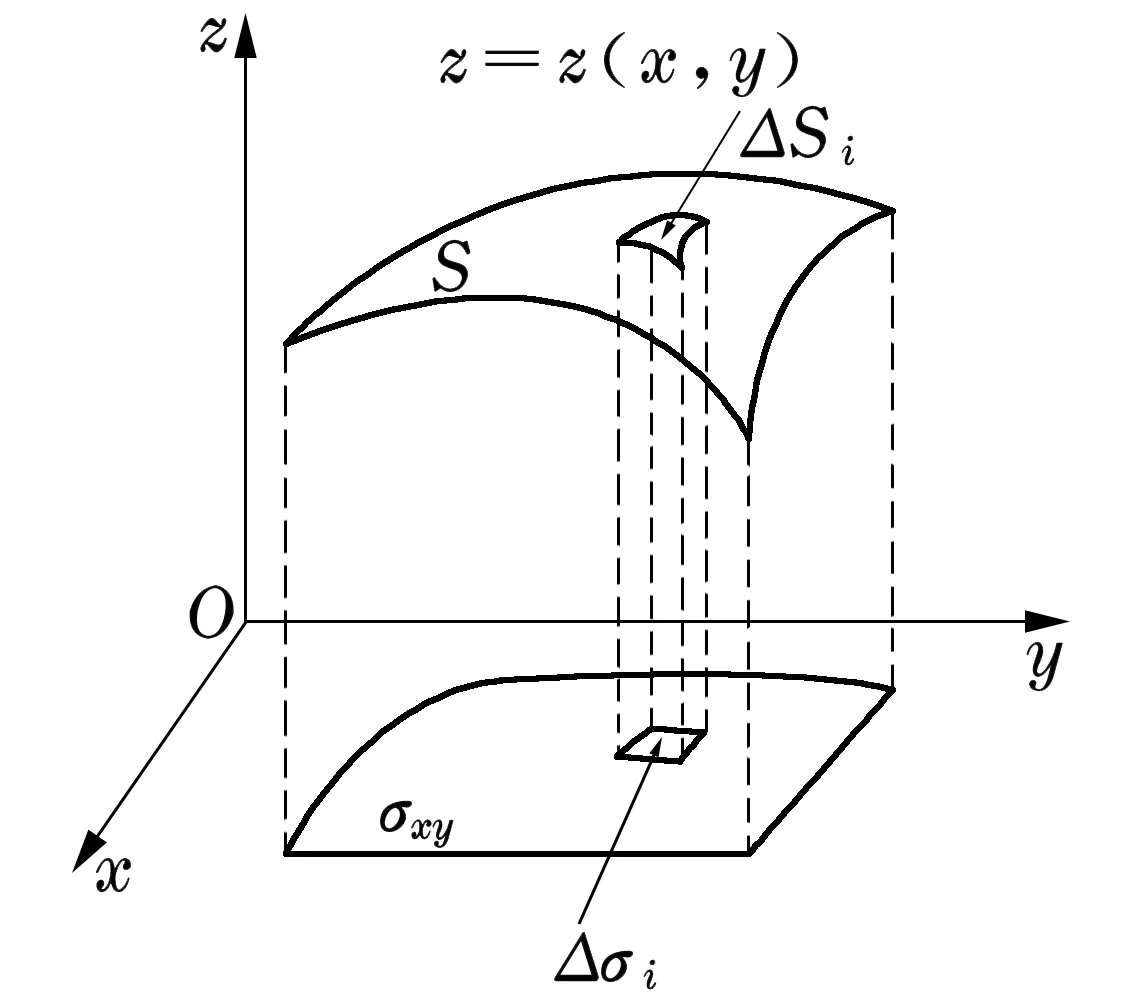
图1 直角坐标系下空间曲面
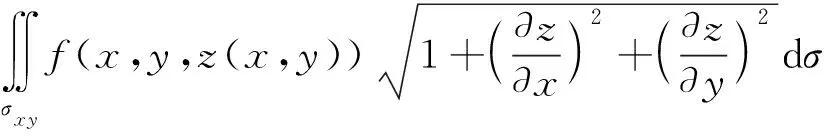
(i) 球面坐标情况:
(ii) 柱面坐标情况:
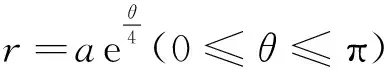
2 理论推导与实例分析

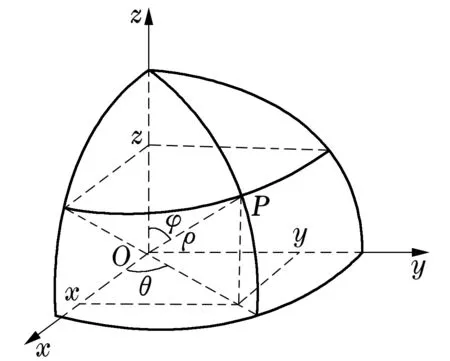
图2 球(面)坐标
点P的直角坐标(x,y,z)与球坐标(ρ,φ,θ)之间的关系为

若空间曲面S的球坐标方程为ρ=ρ(φ,θ)(α1≤φ≤α2,β1≤θ≤β2),其中ρ(φ,θ)具有一阶连续偏导数.这时空间曲面S上点的直角坐标与球坐标的关系为

且有
即
解方程组得
又有
则有
所以第一型曲面积分将化为变量是φ,θ的二重积分

(2)
注 此方法本质上是利用曲面的参数方程来计算第一类曲面积分,这方面已经有结果[4],只不过这里的参数有明显的几何意义:

图3 球面
ρ=常数,以原点为心的球面;
φ=常数,以原点为顶点、z轴为轴的圆锥面;
θ=常数,过z轴的半平面.
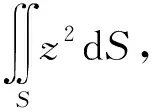
解方法1 如图3,利用公式(1)计算,将S分为
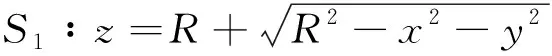
且投影区域均为σxy∶x2+y2≤R2,则

从例1中可以验证了方法的可行性,同时说明有些第一型曲面积分的计算,用球坐标计算由于直角坐标的计算.

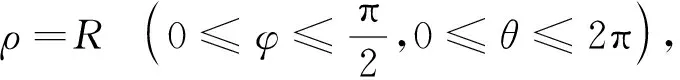
在计算中如果球坐标系下曲面方程ρ=R,其中R为常数(即曲面是球面或球面的一部分),有
说明球面的曲面面积微元为dS=R2sinφdφdθ,该内容对于学生理解三维波动方程的球平均法[5]是有益的.

解取极轴为正z轴,则r,θ相当于球坐标中的ρ,φ.所以球坐标系下旋转面的方程是

图4 对数螺线
如图4.故
从例3中可以看出,有些第一型曲面积分利用球坐标系计算是非常方便的.
3 结 论
对于第一型曲面积分的积分区域是一般的情况,利用直角坐标和球坐标之间的关系,得到第一型曲面积分转化为二重积分的计算表达式,实例表明利用球坐标系计算第一型曲面积分是可行的,丰富了第一型曲面积分的解法.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
