整数环上一类三阶矩阵方程有解的充要条件
2021-05-07黎洪键
黎洪键
(华南师范大学 数学科学学院,广州510631)
1 引 言
随着人们日益对信息安全重视程度的提高,密码学就显得愈来愈重要,而整数矩阵方程的相关研究有助于新密码体系的开发[1].设,分别是全体整数和全体正整数的集合,GLn()表示上n阶可逆矩阵的集合,文献[2-10]考虑一类特殊的整数矩阵集
S(A)={Ak|k,m∈,A∈GLm()}
上的Fermat方程
Xn+Yn=Zn(X,Y,Z∈S(A),n∈)
的可解性问题,显然,研究S(A)的性质有利于这类问题的解决;钟祥贵[11]利用递归关系证明了二阶整数矩阵方程An=kE(E为单位矩阵)有解的充要条件;本文在[11]的基础上,研究三阶整数矩阵方程
An=kE(A∈GL3())
(1)
有解的充要条件.
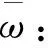
2 引 理
定义1[11]设A是一个m×m矩阵,称使得An=kE,对某个实数k成立的最小正整数n为A的阶,记为O(A).
定义2[12]设G是群,运算记为乘法,a是G中一个元素.如果∀k∈,有ak≠e,则称元素a的阶为无穷.如果∃k∈,使ak=e,则称min{k∈|ak=e}为a的阶.
引理1[12]设a是群G中的一元,a的阶为d,k∈,则

引理2[12]n次单位根的全体Un={x∈|xn=1}对于复数的乘法运算构成一个循环群.
定义3[13]xn-1的根,称为n次单位根,又若n次单位根θ满足θn=1,θm≠1,0 引理3[13]设θ为n次单位原根, 则当且仅当(k,n)=1,θk为n次单位原根, 因而有φ(n)个n次单位原根, 其中,φ(n)为Euler函数, 即小于n且与n互素的正整数的个数. 引理4[13]对n∈有 (ii) φn(x)是整系数的首一多项式; (iii) φn(x)是[x]中不可约多项式. 推论1若θ是n次单位原根, 则扩张次数[(θ):]=φ(n). 定义5[14]令Pn×n表示数域P上n阶方阵的集合, 设A∈Pn×n,若存在正整数m, 使得Am=kE(k≠0), 则称A为数域P上n阶拟幂幺矩阵. 若Am=kE(k≠0), 但对小于m的正整数r, 有Ar≠hE(∀h∈P), 则称m为拟幂幺矩阵A的拟幂幺指数, 记为μ(A)=m. 引理5[14]设A是复数域上n阶拟幂幺矩阵, 则 (i)A的特征值λ满足方程λμ(A)=k(k≠0); (ii)λμ(A)-k是A的零化多项式; (iii)A可对角化. 引理6[15]上的全体代数数组成的集合记为A, 设α∈A, 多项式集合 P=P(α)={f(x)|f(x)∈[x],f(α)=0}, 那么, 对集合P的非零多项式来说, 以下三个性质等价: (i)h(x)是P中次数最低的多项式; (ii)h(x)是P中任一多项式的因式, 即对任一f(x)∈P, 必有q(x)∈[x]使f(x)=q(x)h(x); (iii)h(x)是P中在上不可约的多项式(即[x]中的不可约多项式). 证由于方程(1)有解,因此矩阵A是整数环上3阶拟幂幺矩阵,从而矩阵A也是复数域上3阶拟幂幺矩阵,由引理5(3)可得,存在3阶复可逆矩阵T使得 ⟹ 当O(A)=m时,不妨设Am=λE(λ≠0),于是 于是 因此O(A)≤m. 现在叙述本文的主要结果及其证明. 定理1矩阵方程(1)有解当且仅当矩阵A的阶O(A)∈{1,2,3,4,6}. 证⟹ 当方程(1)有解时,矩阵A的阶显然存在,下面我们对矩阵A的阶O(A)进行分类讨论: 情形1 取 满足A=kE(其中k=a)且O(A)=1,即存在矩阵A使得O(A)=1. 情形2 令 令A2=kE,则有 这等价于 这时,取 可得矩阵 满足A2=kE(其中k=a2+bp+cu)且O(A)=2, 即存在矩阵A使得O(A)=2. 例取 可得矩阵 满足A2=kE(其中k=9)且O(A)=2. 情形3 下面证明当O(A)≥3时,矩阵A的阶O(A)∈{3,4,6}. 设O(A)=m,矩阵A的特征多项式为f(x)且矩阵A的3个特征值为x1,x2,x3,由于det(A)≠0,因此x1x2x3≠0且x1,x2,x3满足下列等式 (2) 由于f(x)是首一三次整系数多项式,因此f(x)的根有三种情形:一个实根和一对共轭复根;三个互不相等的实根;三个实根且至少两个相等.下面对这三种情形进行讨论: (i) 当x1∈时,由公式(2)可得 (x1,x2,x3)=(x2,x3)=(x2). 因此m∈{1,2,3,4,6},即O(A)∈{1,2,3,4,6}, 由于O(A)≥3, 故O(A)∈{3,4,6}; (ii) 当x1∈时,由于O(A)=m,于是由引理5(1)可得由等式(2)得故即 (3) 由于在(ii)这种情形下, 矩阵A的特征多项式f(x)在有理数域上不可约, 由(3)和引理6可得 f(x)|x3±det(A). 由于f(x)是3次首一多项式, 因此 f(x)=x3±det(A). 由于det(A)≠0,于是 f(x)=x3-det(A). (4) 比较(4)左右两端的多项式系数及x1是f(x)的根可得 (5) 综合(i),(ii)可得, 当O(A)≥3时, 矩阵A的阶O(A)∈{3,4,6}. 另一方面,阶为3,4,6的矩阵确实存在 就是阶分别为3,4,6的矩阵的例子. ② 当矩阵A有三个互不相等的实特征值x1,x2,x3时,由于O(A)=m,由引理5(1)可得 由于x1,x2,x3都是实数, 故x1=±x3,x2=±x3, 这与x1,x2,x3两两不等矛盾! (i) 当x1=x2时,此时有x1=x2=x3,由引理5(3)可得,存在3阶复可逆矩阵T使得 这与O(A)≥3矛盾! 故 这与O(A)≥3矛盾! ⟸ 由必要性可知阶为1,2,3,4,6的矩阵均存在, 因此命题成立. 本文研究了整数环上三阶矩阵方程An=kE的求解问题,给出了该方程有解的充要条件.顺利将文献[11]拓展到三阶矩阵情况,解决了该类三阶矩阵方程解的存在性问题. 致谢本文作者非常感谢华南师范大学数学科学学院袁平之教授的鼓励与帮助.
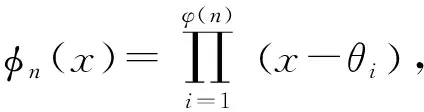


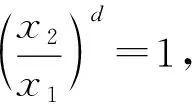
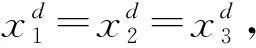
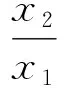


3 主要结果
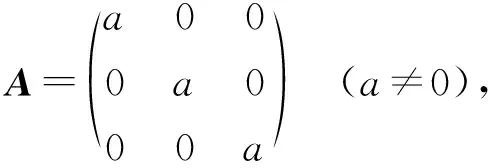









4 结 论
