随机变量和的模函数分布及其应用
2021-05-07叶瑞松
叶瑞松
(汕头大学 数学系, 广东 汕头515063)
1 引 言
在概率论与数理统计的教学中,两个一维连续型随机变量的函数的分布及其相关的概率计算均比较复杂.很多大学生对这部分内容的学习常常理不清头绪,普遍不能够很好地掌握这部分内容,学习费力,效率不佳,可以说是事倍功半,从而导致失去进一步学习的兴趣;对数学专业的学生来说,也将影响其继续学习后续随机数学的相关课程.这其中的原因主要有两个:① 两个一维连续型变量的函数的分布及其概率的计算过程涉及较为复杂的二重积分计算, 包括积分区域的不规则,二次积分上下限的确定,累次积分的准确计算等问题.②传统教材上的例子多数脱离实际,是纯粹理想的数学构造,学生在学习过程未能切身体会其实实在在的应用背景,学习上提不起兴趣[1-4].
笔者根据多年在信号、图像信息领域中经常碰到两幅图像信息或两个信号之间的求和模运算的实际问题,发现研究两个一维随机变量X,Y之和的模函数Z=mod(X+Y,L)的分布及其概率计算,无论在理论上还是应用中均很有意义[5].这个函数在教材中是未作介绍的,但实际上这个函数在图像信息加密和编码中均发挥了很重要的作用,对这个函数的分布的研究很有必要,所得的结果可以用来指导图像信息加密和编码的应用研究.这是对概率论教材中例子的很好补充.由于该函数具有很强的应用背景,对工科学生来讲,能让他们明白该函数应用的领域,了解该函数的应用价值,这对提高他们进一步学习概率统计的兴趣,有很好的激励作用.
目前大多书概率统计的教科书对两个随机变量的和函数的分布问题均有介绍,但是这个和函数的分布在应用中需要改造才能加以应用[6-8].本文针对图像加密领域中两个一维随机变量和的模函数,分别对连续型和离散型的情况进行讨论.虽然在工程应用中碰到的随机变量问题均是离散型的,但是也有必要对其连续型的情况做理论上的探讨,进一步提升学生的数学理论素养.论文从理论上证明了两种情况下的分布函数的相关结果,介绍了该函数在图像信息安全领域的一个应用,并用数值例子验证了相关的理论结果.
2 一维随机变量和的模函数及其分布
首先介绍模函数mod(s,t),该函数是一个二元函数,当两个自变量均是整数时,模函数就是求余数.当两个变量是一般的实数时,表示取模,返回余数,具体地讲,就是将s写成t与一个整数k的乘积和一个落在[0,t)之间的余数之和的形式s=kt+r, 那么mod(s,t)的函数值就是r.将这个模函数应用到随机变量的场合,引进两个一维随机变量X,Y之和的模函数,这是对传统教材上的两个随机变量的和函数的一个推广.
一般灰度图像的亮度值的范围在理论上均是归一化为区间[0,1),所以本文的模函数中的模t一般设为1, 从而函数值的值域也是[0,1).一般的灰度图像的亮度值可以取值0, 所以本文所说的服从均匀分布的随机变量在取值0时,其概率或概率密度与一些教材上的定义稍有不同, 不同之处在于随机变量取值0可以具有正的概率或概率密度.如果两个随机变量X,Y均是区间[0,1)上的均匀分布,将有下面的定理1.
定理1假设连续型随机变量X,Y相互独立,均服从区间[0,1)上的均匀分布,即X,Y~U[0,1).则Z=mod(X+Y,1)的分布也是U[0,1).
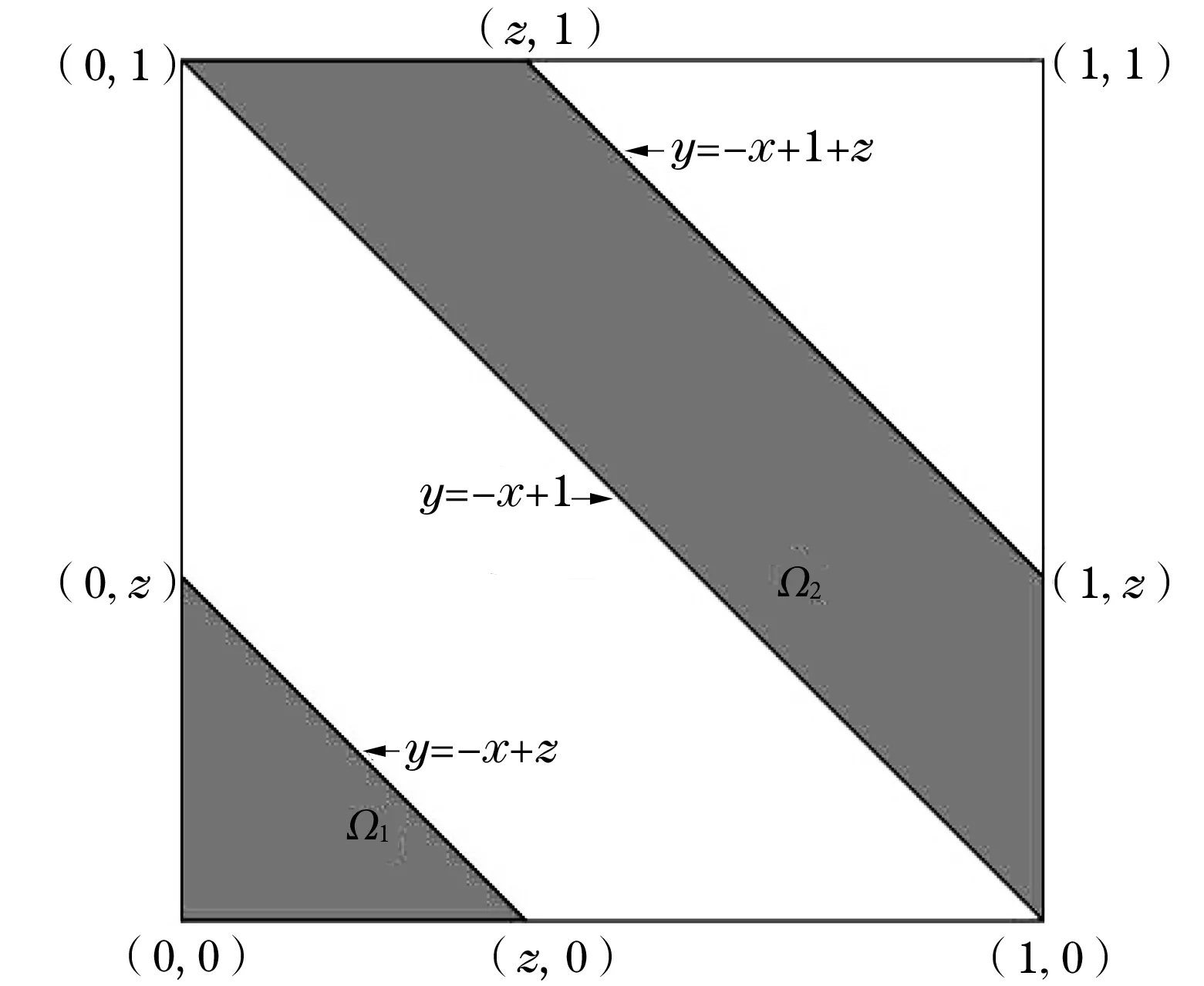
图1 函数Z=mod(X+Y,1)的分布 函数计算示意图
证由于X,Y相互独立,且服从相同的均匀分布U[0,1),其概率密度函数为
所以二维随机变量(X,Y)的联合概率密度函数为

而Z=mod(X+Y,1)的取值在[0,1),假设Z的分布函数为F(z),则
(i)对任意的z≥1,F(z)=P(Z≤z}=1;
(ii)对任意的z<0,F(z)=P(Z≤z}=0;
(iii)对任意的0≤z<1,
F(z)=P(Z≤z}=P{mod(X+Y,1)≤z}=P{0≤X+Y≤z}+P{1≤X+Y≤1+z}
其中,当0≤z<1时,分布函数的计算可以参看图1. 从上面计算所得知道Z~U[0,1).
将随机变量离散化,得到两个随机变量和的模函数的离散型问题,其结果可以用到数字图像的加密领域中设计两幅图像和的模函数.模函数以及和函数的变量均是整数,所以有针对性地选取模为2的幂次数2m,其中m为某一个正整数.具体的应用场合就是数字图像,一幅灰度图像的亮度值可以用m比特的整数来表示,m比特的整数随机变量总共可表示2m个不同的值{0,1,2,…,2m-1},也就是说,如果随机变量X,Y表示m比特的图像的亮度,其取值范围就是{0,1,2,…,2m-1}. 比如m=8比特的数字图像,有28=256个不同灰度层次.定理1的离散型版本即是下面的定理2.
定理2假设离散型随机变量X,Y相互独立,服从相同的均匀分布:
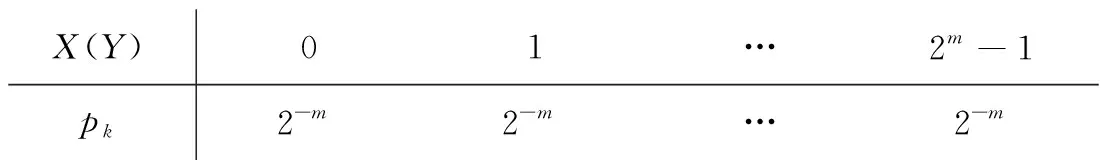
X(Y)01…2m-1pk2-m2-m…2-m
则Z=mod(X+Y,2m)的分布和X,Y的分布相同.
证Z=mod(X+Y,2m)的取值范围为{0,1,2,…,2m-1},所以要得到其分布律,只要计算0≤k≤2m-1时,对应的概率P(Z=k}:
P(Z=k}=P{mod(X+Y,2m)=k}=P{X+Y=k}+P{X+Y=2m+k}
=(2-m)2×(k+1)+(2-m)2×(2m-1-k)=2-m.
所以Z=mod(X+Y,2m)服从和X相同的分布.
到此,得到两个一维相互独立的均匀分布随机变量和的模函数的相关结论.在实际应用场合,均匀分布一般对应类似噪声的信号、图像信息.服从均匀分布的随机变量所表示的图像一般是一幅具有明确内容的明文图像经过加密而得到的密文图像.在应用中,很自然会碰到一个问题,就是一幅具有自然内容的明文图像的加密问题,其中一种办法就是改变图像每个像素的亮度值,从而遮掩了自然图像的内容.密码学要求密文图像要接近均匀分布,越逼近均匀分布,加密性能越好.所以有必要对这个问题进行探讨,如何实现这个加密要求的理想效果,理论上有下面的定理3. 定理3中随机变量X表示某一幅模拟图像的连续型随机变量,其灰度值的范围已经归一化到单位区间[0,1),所以其概率密度函数只是在[0,1)取值,而在[0,1)外的概率密度均为0.
定理3假设连续型随机变量X,Y相互独立,Y~U[0,1),X的概率密度函数为
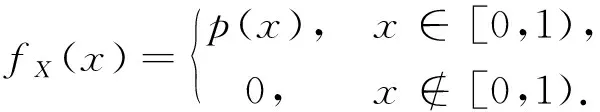
则Z=mod(X+Y,1)的分布也是U[0,1).
证Z的取值范围为[0,1),设Z的分布函数为F(z),则
(i)对任意的z≥1,F(z)=P(Z≤z}=1;
(ii)对任意的z<0,F(z)=P(Z≤z}=0;
(iii)对任意的0≤z<1,
F(z)=P(Z≤z}=P{mod(X+Y,1)≤z}=P{0≤X+Y≤z}+P{1≤X+Y≤1+z}.
由于(X,Y)的联合概率密度函数为
和定理1一样,计算当0≤z<1时的分布函数,可以参看图1,但是这里的计算不能使用Ω1,Ω2的面积作为概率值,需要计算其累次积分.
F(z)=P(Z≤z}=P{(X,Y)∈Ω1}+P{(X,Y)∈Ω2}

所以和定理1结论一样,Z~U[0,1).
同样将定理3中的随机变量离散化,应用到数字图像处理的领域中,也有相应的离散型的定理4.
定理4假设离散型随机变量X,Y相互独立,X服从离散均匀分布:
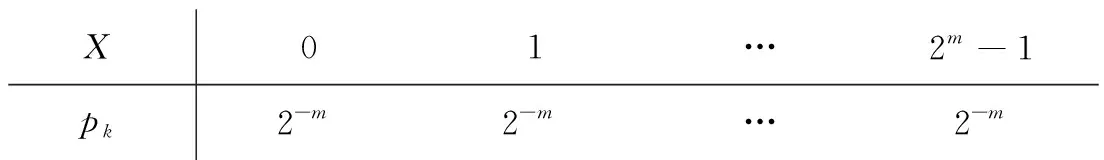
X01…2m-1pk2-m2-m…2-m
Y的分布律为
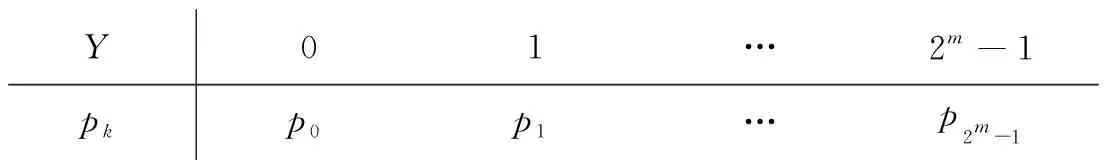
Y01…2m-1pkp0p1…p2m-1
则Z=mod(X+Y,2m)的分布和X的分布相同,也是离散均匀分布.
证Z=mod(X+Y,2m)的取值范围为{0,1,2,…,2m-1},当0≤k≤2m-1时,
P(Z=k}=P{mod(X+Y,2m)=k}=P{X+Y=k}+P{X+Y=2m+k}
=2-m×pk+2-m×pk-1+…+2-m×p0+2-m×p2m-1+…+2-m×pk+1
证明完毕.
更一般地,如果服从均匀分布的随机变量X与另一个服从任意分布的随机变量Y相互独立的话,则可以证明X与Y之和的模函数也一定服从X同样的分布,即有下面的定理5.
定理5假设随机变量X,Y相互独立,X~U[0,b),b>0,Y为任意分布的随机变量,则Z=mod(X+Y,b)的分布也是U[0,b),且与Y相互独立.
证该定理的证明分两步完成.
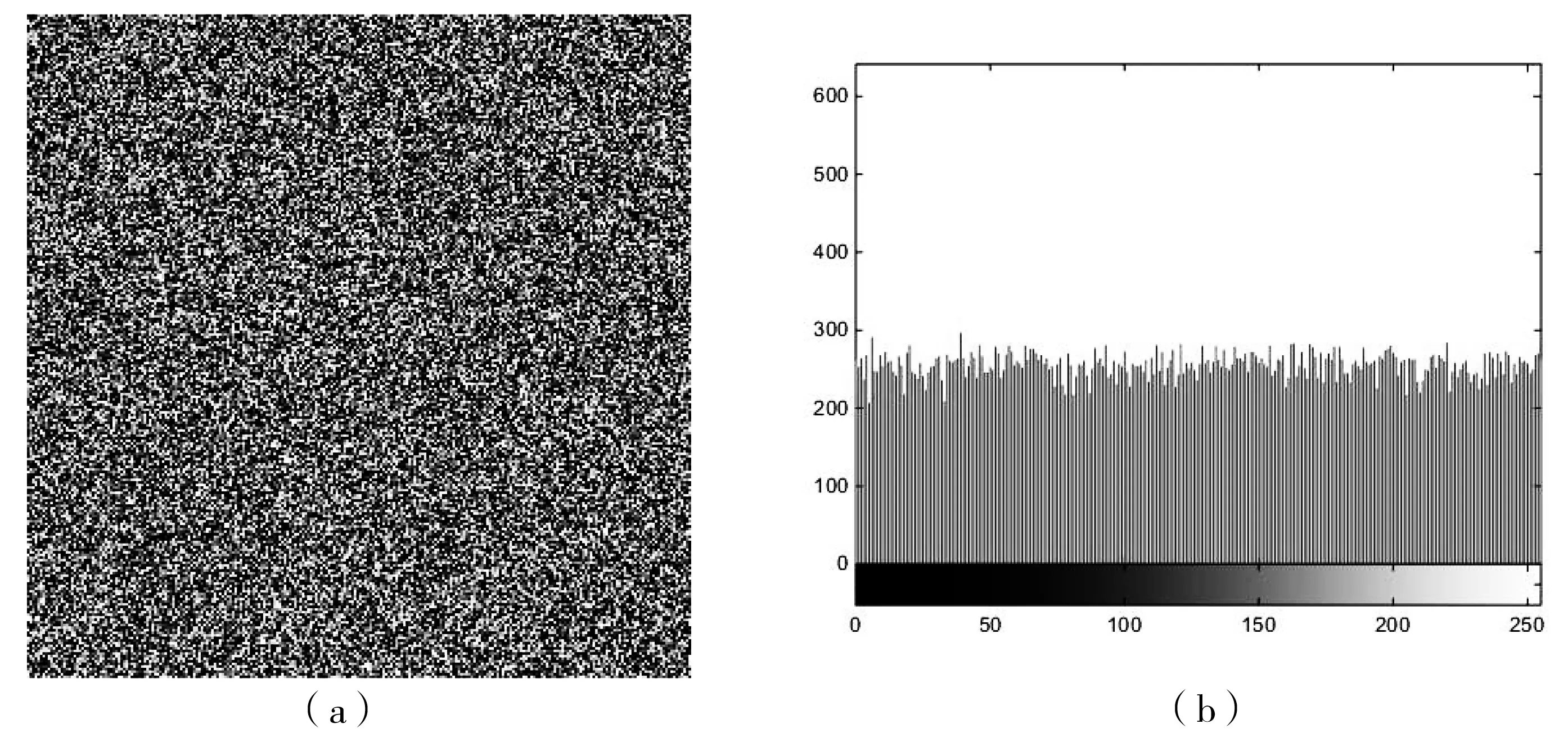
① 对任意常数y,证明Z=mod(X+y,b)~U[0,b).假设y=kb+a,其中k为整数,而0≤a (i) 对任意的z≥b,F(z)=P(Z≤z}=1; (ii) 对任意的z<0,F(z)=P(Z≤z}=0; (iii) 对任意的0≤z F(z)=P(Z≤z}=P{mod(X+a,b)≤z}=P{0≤X+a≤z}+P{b≤X+a≤b+z}. 当a≤z F(z)=P{0≤X≤z-a}+P{b-a≤X≤b-a+z} 当0≤z 综上所述,可知Z=mod(X+y,b)~U[0,b). ② 接着证明对任意随机变量Y,计算Z=mod(X+Y,b)关于Y的条件分布函数也是U[0,b),且与Y相互独立.实际上,假设Z关于Y的条件分布函数为 FZ|Y(z|y)=P{Z≤z|Y=y}=P{mod(X+y,b)≤z}. 则由于Z的取值在[0,b), 且由①的结论知道FZ|Y(z|y)=P{mod(X+y,b)≤z}是U[0,b)的分布函数,且与y值无关,因此证明了定理的结论. 注 该定理的结论是匿名审稿专家所提供的建议,作者将这个结果总结在论文中,并根据专家的思路加以证明.显然定理5的结果拓广前面四个定理的相关结论.其一是不要求随机变量Y的取值范围,可以在整个实轴上取值;其二是不要求Y是连续型的随机变量.对任意的随机变量Y,只要Y与X相互独立,则结论都是成立的.所以定理5的结论更具有概括性,将前面几个定理的结果都可以包括在内,体现了数学的统一性之美. 数学上,灰度数字图像可以用一个二维矩阵A表示,如果图像是8比特即256个灰度级的灰度图像,则A的元素的值属于{0,1,2,…,255}.灰度图像可以表达为一个随机变量X生成的样本,图2(a)为Lena图像,图2(b)为其概率分布.因此,可以用第2节得到的结论来实现两幅图像X,Y之和的模函数运算.如果Y是取值于{0,1,2,…,255}的均匀分布的随机变量,则Y生成的一个二维矩阵样本B,类似于一幅噪声图像,图3(a)为一幅均匀分布的随机变量生成的噪声图像,图3(b)为其概率分布.两幅图像A,B之和的模函数C=mod(A+B,256),得到图像矩阵C,如图4(a)所示,图4(b)为其对应的概率分布.这个结果的图像实际上可以看成隐藏着明文图像Lena的信息的密文图像,其分布也是离散均匀分布,验证了定理4的理论结果.其解密也很容易实现,只要求图4(a)的密文图像矩阵和图3(a)的密钥图像矩阵之差的模函数,即可得到明文图像图2(a):A=mod(C-B,256).这个简单的加密算法很容易用matlab实现,代码如下,供参考: A=imread(‘lena.tif’); %读取8比特灰度明文图像Lena figure, imshow(A); %显示图像Lena figure, imhist(A); %显示图像Lena直方图 [H,W]=size(A); %获取图像的高和宽 B=uint8(floor(rand(H,W)*256)); %生成一幅均匀分布的8比特灰度噪声图像 figure, imshow(B); %显示噪声图像 figure, imhist(B); %显示噪声图像直方图 C=mod(A+B,256); figure, imshow(C); %显示密文图像 figure, imhist(C); %显示密文图像直方图 图2 明文图像Lena及其直方图 图3 密钥图像及其直方图 图4 密文图像及其直方图 本文根据图像信息安全领域中经常碰到的两幅图像信息或两个信号之间的求和模运算的实际问题,探讨了两个一维的相互独立的随机变量X,Y之和的模函数Z=mod(X+Y,L)分布及其概率计算,证明了相关的理论结果,并提供一个具体的应用例子.该函数具有很强的应用背景,对该函数的介绍以及相关理论的证明可以促进大学生进一步理解和掌握随机变量和的模函数的相关知识;具体的信息安全的应用例子将进一步提高大学生学习概率统计的兴趣和动力. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见,特别感谢审稿专家提供了本文的定理5的相关结果和证明思路.3 一个简单的图像加密应用例子


4 结 论
