4上偶长度的LCD负循环码
2021-05-07廖文敬开晓山
廖文敬, 开晓山
(合肥工业大学 数学学院,合肥230601)
1 引 言
上世纪九十年代,Hammons等[1]发现某些高效二元非线性码是环4上线性码的二元象,有限环上编码理论获得重要突破,这使得有限环上纠错码理论成为编码理论研究的一个主要方向之一.Wolfmann在文献[2]中研究了4上奇长度的负循环码及其二元象的性质.此后,有限环上常循环码受到学者们广泛地关注.Blackford在文献[3]中确定了偶长度的负循环码的结构.文献[4]得到了伽罗瓦环GR(2a,m)上负循环码及其自对偶码的生成多项式.文献[5]分析了一般有限环上常循环码的研究方法.文献[6]对pm上长度为n的常循环码的周期分布进行了深入研究,其中gcd(n,p)=1.文献[7-8]利用有限环上常循环码构造了参数较好的量子纠错码.
Massey在文献[9]中引入了有限域上LCD码,证明了LCD码是渐近好码.文献[10]证明了二元LCD码可以用于抗侧信道攻击,这引起了学者们对构造LCD码的极大兴趣.文献[11]研究了有限链环上LCD码的存在性.文献[12]给出了有限链环上LCD循环码的性质.最近,文献[13]证明了有限Frobenius环上不存在非自由LCD码,并且构造了4上最优LCD循环码.
2 预备知识
设f(x)是4上次数为m的首一多项式且f(0)=1或3,定义f(x)的互反多项式为
f*(x)=f(0)-1xmf(1/x).
如果f(x)=f*(x),则称f(x)为4上自互反多项式.设f(x)是4上次数为m的首一基本不可约多项式且deg(f(x))=m,则GR(4,m)=4[x]/〈f(x)〉为4的m次扩环,由伽罗华环相关理论,在GR(4,m)上存在一个(2m-1)次本原单位根ζ使得f(ζ)=0.令Γ={0,1,ζ,…,ζ2m-2},则任意r∈GR(4,m)可以表示成r=a+2b,其中a,b∈Γ.下面引理给出了集合Γ中元素和的性质.

对于奇数n,设β是4扩环中的n次本原单位根,f(x)是4上首一基本不可约多项式,若f(βi)=0,则称f(x)为βi在4上的极小多项式,记为mi(x).

定义x与y的内积为x·y=x0y0+x1y1+…+xN-1yN-1∈4.若x·y=0,则称x与y正交.设C是4上长为N的线性码,定义C的对偶码为若C∩C⊥={0},则称C为4上线性互补对偶(LCD)码.若对任意码字(c0,c1,…,cN-1)∈C,都有(-cN-1,c1,…,cN-2)∈C,则称C为4上长为N的负循环码.视码字c=(c0,c1,…,cN-1)与多项式c(x)=c0+c1x+…+cN-1xN-1相同,则4上长为N的负循环码是商环4[x]/〈xN+1〉的理想.4上长为N的负循环码C与下面两个二元线性码存在密切联系:

设N=2kn,其中k是正整数,n是正奇数.记R=4[x]/〈xN+1〉,则4上长为N的负循环码是环R的理想.根据Hensel引理[13],xn-1在4[x]中可以唯一分解成首一基本不可约多项式的乘积
其中fi(x)(1≤i≤s)是4[x]中首一基本不可约自互反多项式,hj(x)与是4[x]中首一不可约互反多项式对.文献[3,15]中给出4上负循环码的结构.设C是4上长为N的负循环码,则C的生成多项式可以表示为
(1)
其中0≤li,kj,λj≤2k+1,1≤i≤s,1≤j≤t.而且,C⊥的生成多项式为
根据定义,C是4上长为N的LCD码当且仅当C∩C⊥={0}.在R中
因此,C是LCD码当且仅当
max{li,2k+1-li}=max{kj,2k+1-λj}=max{λj,2k+1-kj}=2k+1,
其中1≤i≤s,1≤j≤t.从而,C是4上长为N的LCD码当且仅当li=0或2k+1(1≤i≤s),λj=kj=0或2k+1(1≤j≤t).由此得到下面定理.
定理1设g(x)是定义如式(1),则4上长为N生成多项式为g(x)的负循环码是LCD码当且仅当li=0或2k+1(1≤i≤s),λj=kj=0或2k+1(1≤j≤t).
由定理1可以得到如下推论.
推论1设C是4上长为N生成多项式为g(x)的LCD负循环码,则存在xn-1的自互反因子f(x)∈4[x]使得g(x)=f(x)2k+1.
引理2设f(x)是xn-1在4[x]中的首一因子,则对任意正整数l,在R中有
〈g(x)2k+1〉=〈g(x)2k+1+l〉.

u(x)g(x)2k+1+l=[1-v(x)h(x)2k+1]g(x)2k+1=g(x)2k+1-v(x)(xn-1)2k+1=g(x)2k+1.
因此
〈g(x)2k+1〉=〈g(x)2k+1+l〉.
定理24上长为N的LCD负循环码是自由可逆码.
证设C是4上长为N的LCD负循环码,则存在xn-1的自互反因子f(x)∈4[x]使得C=〈f(x)2k+1〉.容易验证,C是可逆码.设h(x)=(xn-1)/g(x),注意在R中,〈g(x)2kh(x)2k〉=〈2〉,故
C∩〈2〉=〈g(x)2k+1h(x)2k〉=〈2g(x)2k〉.
由引理2得
2C=〈g(x)2k+1+2kh(x)2k〉=〈g(x)2k+1h(x)2k〉=〈2g(x)2k〉,
故C∩〈2〉=2C.根据文献[16]中推论3.12知,C是自由码.
引理3当m≥4是偶数时,Res(C)和Tor(C)的极小汉明距离是3;当m≥4是奇数时,Res(C)和Tor(C)的极小汉明距离至少是5.
证由文献[16]中定理4.2,Res(C)的极小汉明距离等于
当m是奇数时,3不是2m-1的因子,考虑两种情况:
(i) 假设D中含有重量为3的码字c(x),由于D是二元循环码,不失一般性,可设
c(x)=1+xl1+xl2,
其中1≤l1 c(x)+c*(x)=xl2-l1+xl1∈D. 若l2≠2l1,则c(x)+c*(x)的汉明重量为2.若l2=2l1,则c(x)=1+xl1+x2l1. 因此 (ii) 假设D含有重量为4的码字 e(x)=1+xl1+xl2+xl3, 其中1≤l1 e(x)+e*(x)=xl1+xl2+xl3-l2+xl3-l1∈D. 因此 综上所述,当m是奇数时,Res(C)的极小汉明距离至少是5. 定理3当m是偶数时,C的极小Lee距离为3;当m是奇数时,C的极小Lee距离至少为6. 证用dL(C),dH(C)分别表示码C的极小Lee距离和极小汉明距离.由Lee距离的定义,dL(C)≥dH(C).注意到C与Tor(C)的极小汉明距离相同.由引理3,当m是偶数时,dL(C)≥3;当m是奇数时,dL(C)≥5.下面分两种情况讨论dL(C). (i) 当m是偶数时,令l=n/3,则 ζ3l-1=(ζl-1)(ζ2l+ζl+1)=0, 因为ζl-1≠0,所以,ζ2l+ζl+1=0.从而,g(x)整除x2l+xl+1.由此推出 c(x)=(x2l+xl+1)4 是C的码字.在R中,xN=x6l=-1,于是 c(x)=(x2l+xl+1)4=(x4l+2x3l+3x2l+2xl+1)2 =x8l+2x6l+3x4l+2x2l+1=3x4l+x2l+3. 因c(x)的Lee重量为3,故dL(C)≤3.因此,当m是偶数时,dL(C)=3. (ii) 当m是奇数时,假设C含有Lee重量为5的码字c(x),则c(x)一定具有形式 ±(xl1+xl2+xl3-xl4-xl5) 或±(xl1+xl2+xl3+xl4-xl5),其中0≤l1,l2,l3,l4,l5≤n-1且它们彼此不相等.分两种情况讨论: ① 若c(x)=±(xl1+xl2+xl3-xl4-xl5),则 ζl1+ζl2+ζl3=ζl4+ζl5, (2) ζ-l1+ζ-l2+ζ-l3=ζ-l4+ζ-l5. (3) 令ζl1+ζl2+ζl3=ζl4+ζl5=a+2b,其中a,b∈Γ.由引理1可以得到 (ζl1ζl2)1/2+(ζl2ζl3)1/2+(ζl1ζl3)1/2=(ζl4ζl5)1/2. (4) 将(4)式两边平方再模2约化,得到 (5) 类似地,由(3)式可以得到 (6) (6)式可变形为 (7) 将(2)式模2约化后代入(7)式,得到 (8) 将(3)式模2约化,并变形为 结合(5)式得到 (9) ② 若c(x)=±(xl1+xl2+xl3+xl4-xl5),则有 ζl1+ζl2+ζl3+ζl4=ζl5,ζ-l1+ζ-l2+ζ-l3+ζ-l4=ζ-l5. 由此推出 ζa+ζb+ζc+ζd=1, (10) ζ-a+ζ-b+ζ-c+ζ-d=1, (11) 其中a=l1-l5,b=l2-l5,c=l3-l5,d=l4-l5.对(10)式运用引理1,再两边平方并模2约化,得到 (12) (13) f(x)=x4+x3+λx+λ=(x+1)(x3+λ)=0. 根据文献[14]中引理9.5,x3+λ=0在F2m最多只有一个根.因此,方程f(x)=0在F2m中最多只有两个根,矛盾. 综合①和②,当m是奇数时,C中没有Lee重量为5的码字.所以,dL(C)≥6. 例设m=5,n=31,N=62.在4[x]中, g(x)=m1(x)m-1(x)=(x5+2x4+x3+3)(x5+3x2+2x+3) =x10+2x9+x8+3x7+x5+3x3+x2+2x+1. 设C=〈g(x)4〉是4上长为62的LCD负循环码,其中 g(x)4=x40+2x36+2x34+x32+x28+2x22+3x20+2x18+x12+2x6+2x4+1. 根据定理3可知,C的Lee距离至少为6.利用MAGAMA程序算出C的Lee距离为6.因此,C是4上参数(62,284,6)的线性码. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.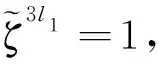

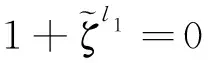
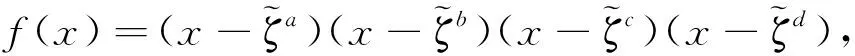

5 结 论
