超声-MIG焊熔滴过渡的数值模拟

2021-05-07黄泽湃李会军王瑞超王皓

焊接 2021年2期

黄泽湃，李会军，王瑞超，王皓

(五邑大学，广东江门 529020)

0 前言

熔化极惰性气体保护焊(MIG)具有焊接生产率高、成本低、熔敷率高等优点，被广泛应用于工业生产中[1]。在焊接过程中熔滴的尺寸大小、过渡频率和脱落速度等是影响焊缝质量和焊接稳定性的重要因素[2]，为了实现对熔滴过渡行为的控制，近年来有学者提出了利用超声辐射力促进熔滴过渡的熔化极复合焊接方法，即超声-MIG焊。通过在MIG焊中添加超声作用既能提高焊接效率、改善焊缝组织，又能压缩电弧使飞溅减小[3-4]。范成磊等人[5]通过采用高速摄像的方法观测并分析熔滴过渡过程，研究在不同焊接参数下超声-MIG焊过渡区间的变化情况；谢伟峰等人[6]结合焊接电弧、熔滴过渡及焊缝成形三者之间的关系及各自特点，探讨了在超声-MIG焊接过程中超声的作用规律。该文将通过数值模拟的方式研究超声-MIG焊熔滴过渡机制，利用FLUENT软件模拟在超声的作用下熔滴长大、变形和脱落的过程，并将其与相关试验进行对比，分析在不同焊接电流和超声振幅条件下熔滴过渡的变化规律。

1 数值模拟

1.1 物理模型

超声-MIG焊金属熔滴从焊丝端部脱离转移到熔池的过程中受到了重力、表面张力、电磁力、等离子流力和声辐射力的综合影响。其熔滴过渡过程是个涉及多场耦合的复杂物理过程，为了便于描述此过程、简化计算，作如下假设[7]：①液态金属熔滴为不可压缩牛顿流体；②焊丝端部呈水平，熔滴初始状态为半圆形；③熔滴过渡中的物理参数不随温度的变化而变化；④忽略超声的空化作用。所建立的熔滴过渡简化模型如图1所示，熔滴从焊丝端部ab流出，滴落至工件ef；氩气从保护气体入口cd, gh导入，流向压力出口de, gf。图中焊丝ab直径为1.2 mm，保护气体入口cd, gh宽度为3.4 mm，气体压力出口de, gf宽度为8 mm，网格尺寸为0.05 mm。

图1 熔滴过渡的简化物理模型

1.2 控制方程

质量守恒方程：

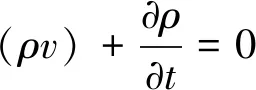
(1)

动量守恒方程：

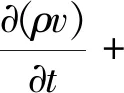
(2)

电流连续方程：

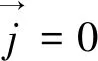
(3)

欧姆定律：

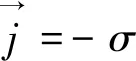
(4)

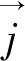
(5)

式中:CD为等离子流阻力系数；Ap为熔滴径向截面积；ρf为等离子流密度；vf为等离子流的流速。

熔滴所受表面张力采用连续表面张力模型(Continuum surface force, CSF)表示，即：

(6)

式中:γij为表面张力系数；κi为自由表面曲率；αi为体积分数。

根据洛伦兹力定律，熔滴所受电磁力：

(7)

熔滴电流密度分布采用文献[8]中所提出的高斯分布，轴向和径向电流密度为：

(8)

(9)

式中:Rw为焊丝半径；z为离焊丝端部的距离；H为熔滴的长度；k为电流集中系数；I为焊接电流；r为熔滴的横截面半径。

根据安培定律，电流所产生的磁场强度为：

(10)

熔滴过渡中受到的声辐射力：

(11)

式中：R0为熔滴半径；ω为角频率；ρ0为传播介质密度，取1.78 kg/m3；c为超声的声速，取319 m/s；p0为声压；k为波数；z为小球距反射面距离。

熔滴内部受力分析如图2所示，径向受到电磁收缩力的作用，轴向受到促进熔滴过渡的重力、等离子流力、轴向电磁力和阻碍熔滴过渡的表面张力及呈周期变化的声辐射力。图中将超声作用近似看作平面驻波[9]，所以熔滴所受的声辐射力会随熔滴距离反射端的位置变化而变化。

图2 熔滴受力分析

熔滴过渡模拟采用VOF(Volume of fraction)方法实现对金属熔滴的液面流动进行追踪[10-13]，VOF方法是通过引入流体体积函数F(i，j，t)来计算不同时间下各相所占的体积分数变化，其满足如下方程：

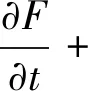
(12)

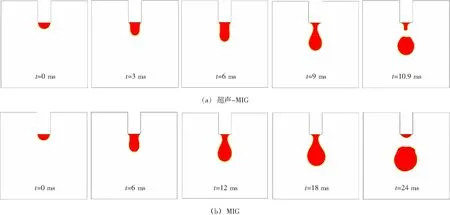
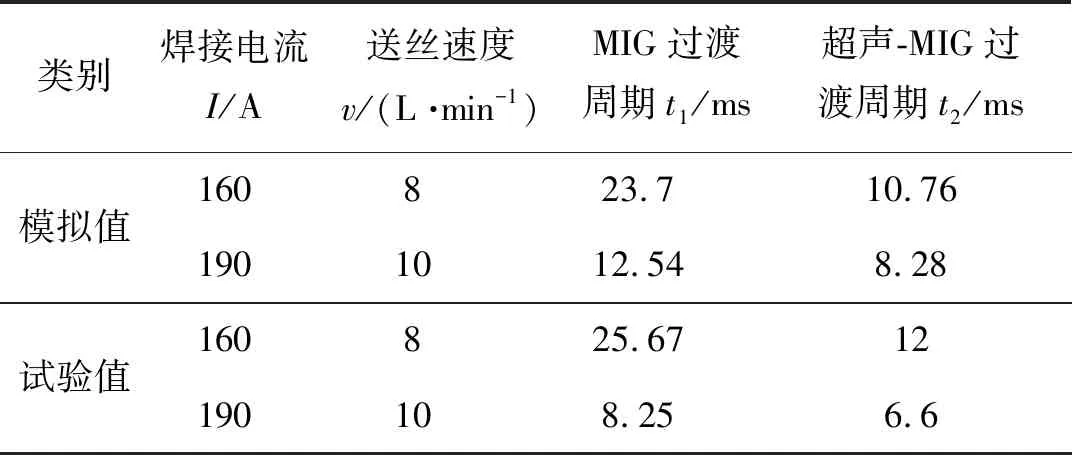
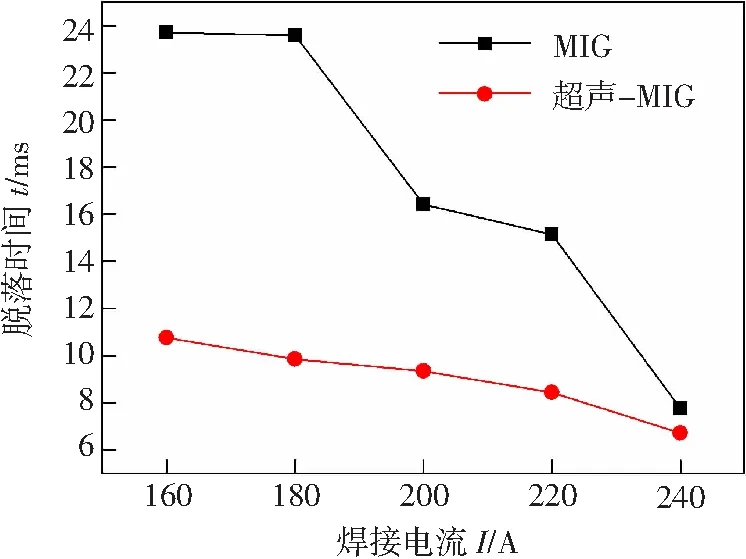
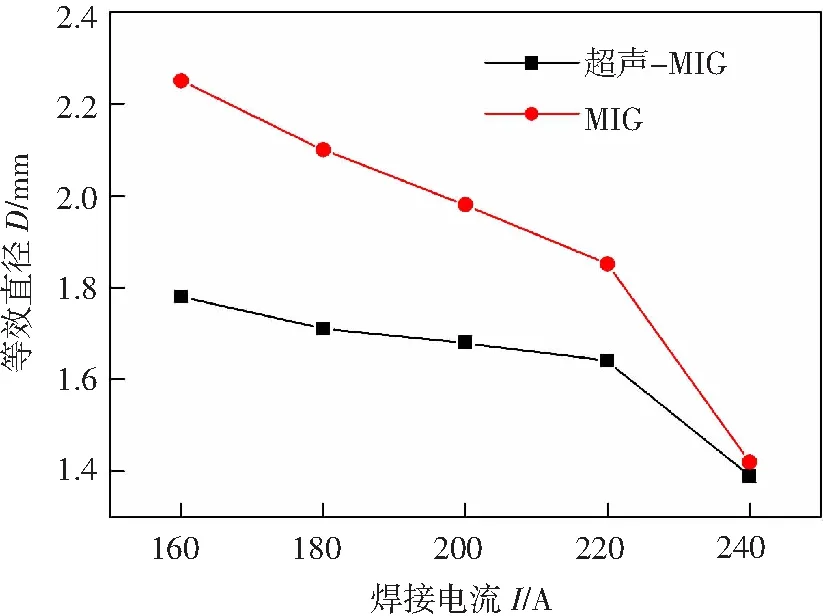
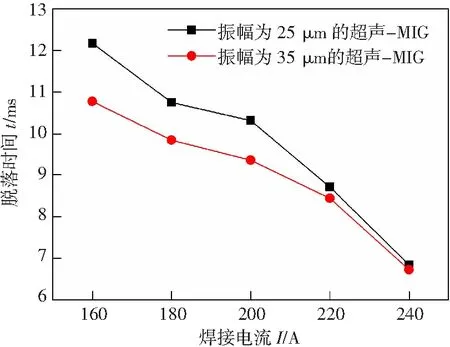
式中：如果F=1时表示单元格中充满液体；当0

1.3边界条件

表1为超声-MIG熔滴过渡数值模拟所需设置的边界条件，其中vf为送丝速度，vg为保护气体流速。为了模拟超声振动的效果，将焊丝端部ab和两侧bc，ah设置为运动边界，保护气体入口cd，gh设置为变形边界。

表1 边界条件

2 模拟结果与讨论

利用FLUENT软件模拟同轴式超声-MIG焊熔滴过渡过程，通过向动量方程添加源项的方式使金属熔滴受到电磁力、等离子流力、声辐射力的作用，并结合动网格运动模拟超声振动过程。焊丝采用直径为1.2 mm的5356铝合金焊丝，其物理性能参数见表2。超声参数挑选最佳的声场参数[14]，端面振幅为35 μm，超声频率为20 kHz。

表2 5356铝合金的物理性能参数

2.1 焊接电流的影响

图3a为送丝速度为8 m/min、焊接电流为160 A时超声-MIG焊熔滴过渡的轮廓变化。初始时刻熔滴呈半圆形状，在0～6.6 ms时，熔滴受到轴向电磁力、重力、等离子流力的促进作用和表面张力、超声辐射力的阻碍作用，开始逐渐变形、慢慢被拉长。在6.6～10.9 ms时，超声辐射力方向发生改变，表现为向下轴向力，促进熔滴过渡。在熔滴进一步被拉伸过程中颈部受径向电磁力的影响开始收缩，快速形成水滴状。随着熔滴进一步长大，颈部截面积也在不断收缩，当促进熔滴过渡的轴向合力大于表面张力时，熔滴就会从焊丝端部脱落实现滴状过渡，即在t=10.76 ms时熔滴脱离,此时过渡熔滴直径为1.78 mm。相对于同一条件下的常规MIG焊熔滴过渡过程，如图3b所示，在6.6 ms前超声-MIG焊与MIG焊熔滴轮廓变化区别较小，这是由于声辐射力的阻碍作用随熔滴高度变化呈现逐渐减小的状态，所以此时声辐射力相对于其他轴向力影响作用较小，而在6.6 ms后超声-MIG焊熔滴所受声辐射力转变为促进作用力且逐渐增大，加快了熔滴形成缩颈的过程，从而缩短了熔滴脱落时间。通过对比可知，超声-MIG焊的过渡频率相对更快，脱落尺寸相对更小。

图3 熔滴过渡轮廓变化

图4为超声-MIG焊和MIG焊熔滴内部压力的分布情况，由图可知，熔滴由于受径向电磁力的作用，缩颈处压力值为负值，表现为向内收缩力，轴向受等离子流力、表面张力、轴向电磁力和声辐射力的综合作用，熔滴端部压力为正值，表现为向下轴向力。超声-MIG熔滴在脱落过程中由于受到超声振动的影响，焊丝边界发生周期性运动，导致内部径向受力呈不对称分布，这种随时间摇摆变化的径向受力使熔滴更容易脱落，轴向在超声辐射力的增添下也进一步加快熔滴过渡。将MIG和超声-MIG焊熔滴过渡周期与文献[5]、[15]中的试验值进行比较，见表3，结果表明二者大致吻合，但是在较大电流条件下其过渡周期与试验结果相比存在一定的误差，这可能是因为模拟时所添加的电磁力与实际情况存在差异和未考虑熔滴滴落至熔池的时间所导致。

表3 模拟值与试验值的对比情况

图4 压力分布云图

图5为送丝速度为8 m/min而不同焊接电流条件下的MIG焊和超声-MIG焊的熔滴脱落时间。随着焊接电流的逐渐增加，MIG与超声-MIG焊熔滴脱落时间都呈递减的趋势，MIG焊熔滴过渡周期随焊接电流变化的程度比较明显，熔滴过渡类型由大滴过渡向射滴过渡转变；而超声-MIG焊熔滴过渡周期相对较短且变化曲线较缓。对比结果发现，在较小的电流条件下，MIG与超声-MIG焊的脱落时间相差较大，而随着焊接电流的增加，这种差距逐渐减小。这是由于在小电流的作用下熔滴内部电磁力较小，主要受重力和表面张力的影响，而在添加超声作用后熔滴受声辐射力和超声振动的影响，所以产生的变化较为明显；随着焊接电流的增加熔滴所受的电磁力也随之增加，在较大的电流下促进熔滴脱落的电磁力起决定性作用，所以受超声影响产生的变化就相对较小。图6为相对应的MIG和超声-MIG过渡熔滴的等效直径，在小电流的条件下MIG焊熔滴的脱落尺寸较大，而超声-MIG焊熔滴在超声作用下过渡尺寸明显变小，当焊接电流增加到240 A时，MIG与超声-MIG熔滴过渡尺寸大小相近。

图5 不同焊接电流下MIG与超声-MIG的熔滴脱落时间

图6 不同焊接电流下MIG与超声-MIG熔滴等效直径

2.2 超声振幅的影响

超声振幅是影响超声振动的重要参数，也是决定声辐射力大小的关键因素。图7为超声振幅为25 μm和35 μm时超声-MIG焊熔滴的脱落时间。对比二者曲线发现，当振幅为35 μm时的熔滴过渡周期整体上会比振幅为25 μm的短，这也就表明了由于超声振幅的增加导致超声辐射力的增大和焊丝振动幅度的增大进而会在一定程度上使熔滴脱落时间缩短，加快熔滴过渡频率。但是从图可知，当焊接电流为160 A时，振幅为35 μm的超声-MIG焊比振幅为25 μm的熔滴脱落时间快约1.4 ms，而当焊接电流为240 A时，两者相差为0.12 ms，这是因为在大电流下熔滴过渡受电磁力的主导作用，所以随着电流的增加超声辐射力的影响作用逐渐减小，而两者相差幅度不大，主要是因为振幅相差较小所以其整体变化并不会太明显，以致于其熔滴脱落尺寸也不会随之有太大的变化。