板厚对不锈钢车体激光叠焊接头抗剪强度和疲劳强度的影响

2021-05-07罗超张锦华王琰刘海玲李希勇

焊接 2021年2期

罗超，张锦华，王琰，刘海玲，李希勇

(中车唐山机车车辆有限公司，河北唐山 063035)

0 前言

轨道客车不锈钢车体在制造过程中通常使用电阻点焊成形[1-2]。由于电阻点焊变形大、密封性差、接头静强度低及疲劳强度低等问题，最近车体制造部门尝试用具有焊接变形小、焊接速度快及连续焊接密封性好等优点的激光叠焊替代电阻电焊进行不锈钢车体成形[3-5]。列车在运行过程中，车体不仅承受静载荷还承受振动载荷，因此，研究人员需要通过试验和理论分析掌握影响焊接结构抗剪强度和疲劳强度的主要因素，包括焊板厚度对抗剪强度和疲劳强度的影响规律等，从而为设计人员提供强度优化设计指导[6-12]。文献[13]报道了SUS301L不锈钢非熔透型激光搭接焊的疲劳特性，发现焊板厚度对焊接接头的抗剪强度和疲劳强度具有一定的影响，但其影响机理并不十分清楚。

针对上述问题，作者开展了2种不同板厚搭配的不锈钢激光叠焊接头的疲劳试验，测试了相应的抗剪强度-变形曲线和疲劳强度-寿命曲线，观察了拉伸破坏特征和疲劳裂纹萌生位置、扩展特征，分析了板厚对抗剪强度和疲劳强度的影响。

1 拉伸与疲劳试验

拉伸试样和疲劳试样均由2块不锈钢板经激光叠焊连接而成，其形状和尺寸如图1所示。图中t1和t2为不锈钢板的厚度，该研究对板厚搭配不同的2种试样进行试验。由板厚t1=0.8 mm和t2=2 mm焊接而成的试样简称0.8+2试样；由板厚t1=2 mm和t2=2 mm焊接而成的试样简称2+2试样。焊接工艺参数见表1。0.8 mm厚不锈钢板的材料为SUS301L-3/4H；2 mm厚不锈钢板的材料为SUS301L-1/4H。试验前，对焊缝两边和中间3个部位进行了焊缝尺寸的观测，如图2所示。0.8+2试样焊缝下板的熔宽和熔深的均值分别为0.79 mm和0.57 mm；2+2试样焊缝下板的熔宽和熔深的均值分别为1.13 mm和0.78 mm。2+2试样的熔宽和熔深均大于0.8+2试样的相应值。

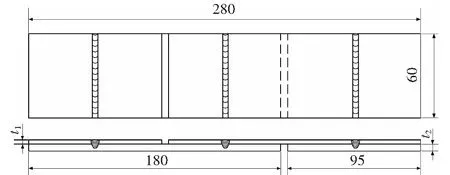
图1 试样的形状和尺寸

表1 焊接工艺参数

图2 焊缝尺寸观察结果

拉伸试验在岛津电液伺服疲劳试验机上进行，试验采用位移控制，加载速度设定为0.01 mm/s。疲劳试验在Rumul电磁共振疲劳试验机上进行，应力比R设定为0.5，以试样发生疲劳断裂或循环受载达到1×107周次作为停机条件。

2 结果与分析

2.1 抗剪强度

拉伸加载后，试样的焊接部位受剪切力作用，试样的破坏表现为剪切破坏，具体破坏形式如图3所示。由图3a和图3b可知，0.8+2试样和2+2试样的破坏形式完全相同，均为2个焊板在焊肉部位被剪断，2个焊板完全脱开，剪断后的焊板发生翘曲变形。

图3 拉伸试样断口形貌

在同一条件下分别对6件0.8+2试样和2+2试样进行拉伸试验，获得的拉伸曲线如图4所示。可见，2种试样的拉伸曲线均可分为弹性(倾斜)部分和塑性(水平)部分，0.8+2试样的倾斜部分较陡(弹性变形小)、水平部分较长(塑性变形大)；2+2试样的倾斜部分较缓(弹性变形大)、水平部分较短(塑性变形小)。0.8+2试样的剪切力平均值为32.96 kN，标准偏差为1.15 kN；2+2试样的剪切力平均值为49.5 kN，标准偏差为2.42 kN；2+2试样的剪切力明显高于0.8+2试样的相应值。

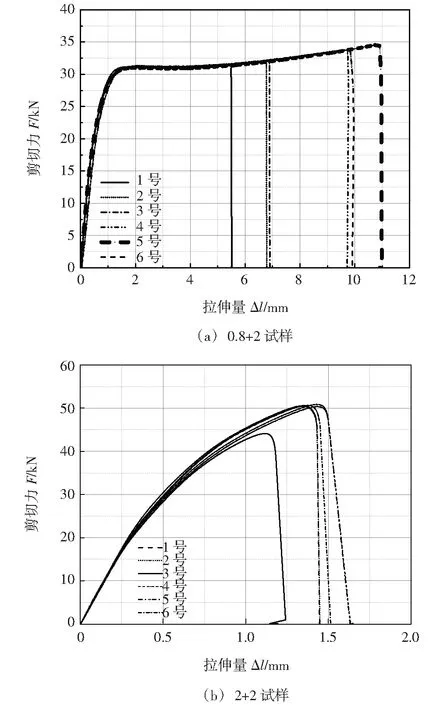
图4 焊接接头的剪切拉伸曲线

由于2种接头破坏均表现为焊缝部位的剪切破坏，焊接接头的抗剪强度主要取决于叠焊接头熔宽和焊缝抗剪强度，即断裂时的载荷/(熔宽×试样宽度)。0.8+2试样和2+2试样的熔宽均值分别为0.79 mm和1.13 mm，后者约为前者的1.43倍。0.8+2试样和2+2试样焊缝的抗剪强度分别为694 MPa和730 MPa，后者约为前者的1.05。可见，2种试样熔宽尺寸的不同是造成抗剪强度差异的主要原因。

2.2 疲劳强度

疲劳断裂位置的观察如图5所示。由图可知，2种试样的疲劳裂纹均发生在下焊板(未焊透焊板)的焊核边缘处。图5所示为开裂焊板的裂纹起始位置观察。图6a和图6b分别是对图5中B部分从左侧向右侧的放大观察。可见，裂纹起始于2个焊板之间的内表面靠近焊核处，然后向焊板的外表面扩展，图中最上部竖向的条线是裂纹起始于不同平面后扩展形成的，属于典型的疲劳裂纹扩展特征。综合图5和图6可知，疲劳裂纹萌生于未被夹持的未焊透板内表面靠近焊核附近热影响区，裂纹沿着焊核边缘向板外表面方向扩展，直至穿透焊板。

图5 疲劳试样断口形貌

图6 裂纹起始位置和扩展方向的微观观察

从断口观察可知，所有疲劳断裂均发生在未焊透板(2 mm板)。因此，试验数据的疲劳强度-寿命关系可用图7所示的未焊透板的名义应力幅变程-寿命(ΔS-N)曲线表示。由图可知，在高应力，2种接头的疲劳寿命没有明显的差别，但是在低应力，2+2试样的疲劳强度明显大于0.8+2试样的相应值。其中，0.8+2试样的1×107周次的疲劳强度为33 MPa，而2+2试样的1×107周次的疲劳强度为50 MPa。

图7 焊接接头的疲劳应力变程-寿命(ΔS-N)曲线

3 有限元分析

3.1 有限元模型

为了弄清板厚对2种接头抗剪强度和疲劳强度的影响，该节通过有限元方法对2种接头进行了高、低2种名义应力(50 MPa和100 MPa)的加载(计算名义应力的板厚按2 mm考虑)。

按照图1所示的试样进行有限元建模，焊缝连接区域的面积为平均熔宽乘以试样宽度。为了避免尖锐缺口带来的计算不稳定性，将焊缝边缘2个焊板间的尖端缺口按半径R为0.01mm的圆弧形缺口处理，并在该区域采用R/10的网格进行划分，以保证获得收敛的缺口应力值。对于远离焊缝缺口尖端的区域，采用逐渐变化的过渡网格进行划分，直至网格尺寸达到约0.25 mm。对于2+2试样的叠焊接头，计算单元数为26 256，节点数为27 911；对于2+0.8试样的叠焊接头，计算单元数为20 732，节点数为22 328。考虑到模型加载时处于平面拉伸状态，因此计算时按平面应变处理，在Abaqus中采用带有减缩积分的4节点线性平面应变单元进行分析。

为简化计算，仿真分析中不考虑熔核、热影响区和母材之间的材料差异，参考文献[14]的试验数据，取材料的弹性模量E=84 550 MPa，泊松比v=0.3，初始屈服强度σs=316 MPa，采用等向强化模型计算材料的塑性行为，材料的应力-应变曲线[15]如图8所示。在夹持区域除加载方向以外的所有自由度，将该端部节点与参考点耦合，并在参考点上施加集中力载荷Fb。

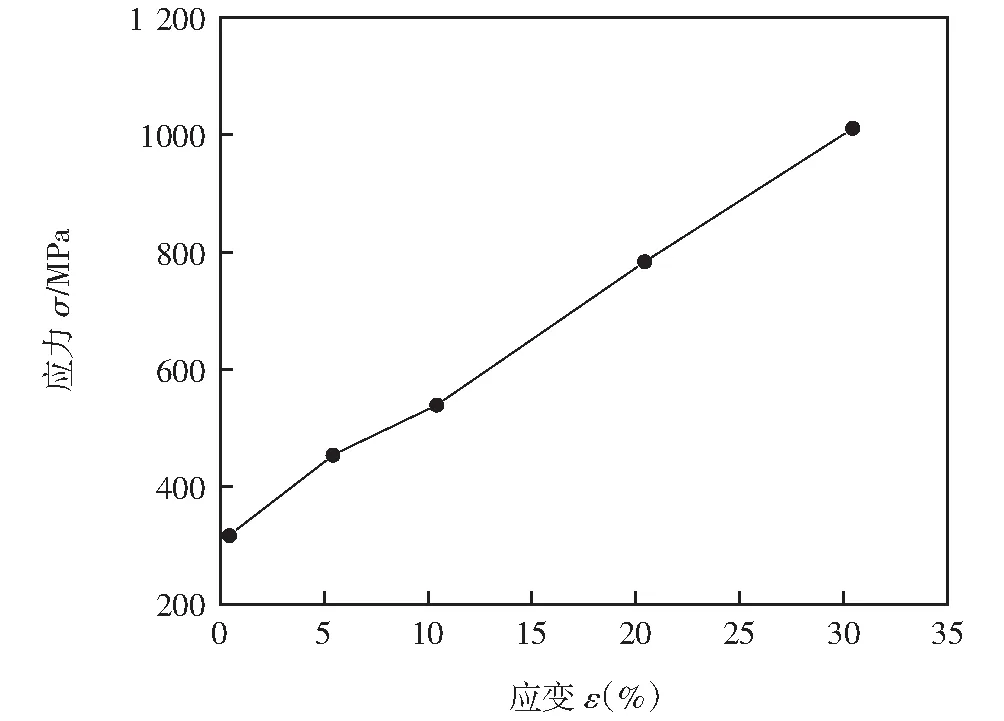
图8 材料应力-应变曲线

3.2 计算结果

在施加线载荷100 N/mm时，2种焊接接头试样的变形云图如图9所示。可见，在相同线载荷条件下，2+0.8试样的变形量大于2+2试样。

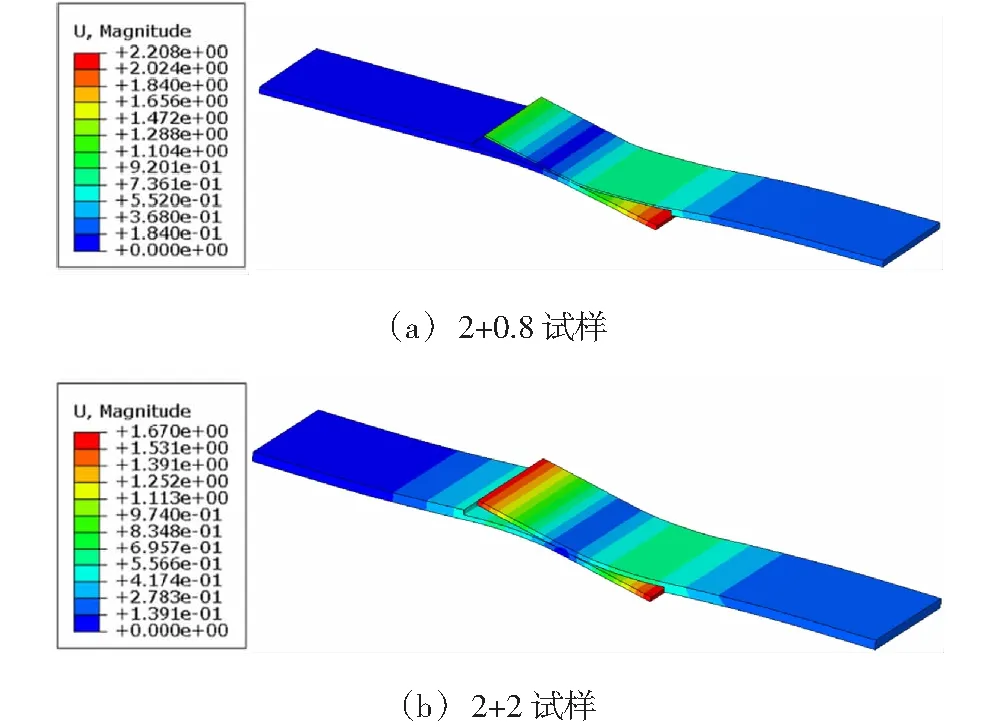
图9 焊接接头的变形云图

在2种叠焊接头中，以2 mm厚板的面积计算名义应力值，分别得到当名义应力值为50 MPa和100 MPa时2种叠焊接头在缺口区域的轴向应力(S11)分布，如图10所示(焊核两侧左右两缺口对称，图中仅给出左侧)。图中横轴是2个焊板之间靠近焊核左侧位置处缺口周围从位置A开始经过位置B到位置C的距离。口区域的应力分布近呈现对称规律，数值计算结果还表明焊缝两端缺口也同样满足反对称的分布规律。在2种载荷的作用下，2+0.8叠焊接头的峰值应力均大于2+2叠焊接头的峰值应力，表明2+0.8叠焊接头在缺口区域的应力集中更为严重；随着载荷的增大，受缺口区域塑性变形的影响，2种叠焊接头峰值应力之间的差距略有减小。

图10 2种叠焊接头焊核边缘左侧缺口应力对比

这与高应力区0.8+2试样叠焊接头的疲劳强度与2+2试样叠焊接头的疲劳强度接近，而低应力区0.8+2试样叠焊接头的疲劳强度小于2+2试样叠焊接头的疲劳强度的结果对应。可见2种试样在高、低应力区的应力集中程度的差异是引起疲劳强度差异的主要因素。焊接接头的应力集中程度可以通过应力集中系数来反映，应力集中系数定义为缺口应力与远端名义应力的比值，当焊接接头远端的名义应力一致时，缺口应力的大小即可反映焊接接头的应力集中程度。而缺口应力的大小主要由缺口半径和焊接接头的板厚共同决定。由于2种叠焊接头采用相同的焊接工艺，因此文中在计算中假定接头具有相同的缺口半径。对于厚度较薄的叠焊接头，缺口区域材料的约束作用较弱，因此缺口应力大于较厚的叠焊接头，应力集中程度较高，疲劳强度较低。