一种能给出充油电气设备油色谱故障诊断可靠性的神经网络方法
2021-05-07张宝全马雅丽白诗婷胡伟涛徐志钮
张宝全, 马雅丽, 关 睿, 白诗婷, 李 静, 胡伟涛, 徐志钮
(1.国网河北省电力有限公司检修分公司, 石家庄 050011; 2. 华北电力大学电气与电子工程学院, 保定 071003)
绝缘油绝缘性能优异,同时又具有一定的散热功能,从而延缓绝缘老化速度,在大型电气设备经常采用油作为其内绝缘材料。因此,充油电气设备在电力系统中应用广泛。通常来说设备的寿命取决于其绝缘的寿命,内绝缘在长期电压、温升等作用下会逐渐老化发生故障,如何预警故障、避免停电的发生非常重要。
在充油电气设备的诸多诊断方法中,油中溶解气体分析方法(又称油色谱方法)[1]由于能有效检测各种程度的过热、局部放电和局部的火花和电弧放电故障,同时检测时无需停电、便于在线监测,尤其对于局部、慢性、潜在性缺陷的检测非常有效,在电力设备预防性试验规程中排名第一。在采用气相色谱仪测得充油电气设备中故障特征气体浓度后如何根据特征气体浓度检测故障类型成了关键问题。早期的特征气体法根据特征气体浓度和占比来判断故障类型,该方法比较直观、方便,但缺乏量化,要求使用者具有较好的油色谱故障诊断经验。为了提高诊断方法的易用性,国际电工委员会(international electrotechnical commission, IEC)在热力动力原理和实践的基础上,从5种特征气体中选择3对溶解度和扩散系数比较相近的组成3对比值,根据比值确定编码,根据编码确定故障类型,目前最为常见的是改良IEC三比值法[2]。为了提高对充油变压器导电回路和磁回路的铁芯多点接地故障诊断的准确性,人们又提出了四比值法[2]。针对比值法可能存在的实际特征气体无法找到编码从而无法诊断故障的问题,中国学者杜洋提出了无编码的比值法[3],提高了基于油色谱的故障诊断准确性。以上比值法有效推动了充油电气设备故障诊断的进步,但也存在诊断准确性不够高、不能进一步利用长期实测得到的大量特征气体浓度数据隐含的信息来提高故障诊断的准确性等问题。为了解决该问题,人们提出采用机器学习来提高故障诊断的有效性,有基于神经网络(artificial neural network, ANN)[4-6]、粗糙集[7]、Petri网[8]、遗传算法[9]、深度学习[10]、证据推理[11-12]、模糊数学[13]等方式,有效推动了充油电气设备故障诊断的智能化,尤其是神经网络方法由于具有较好的自学习能力而被广泛应用。人们在网络类型选择[14-16]、训练性能提升[17-18]、网络结构优化[19]、泛化能力增强[19]等方面进行了大量的研究,取得了长足的进步。但是现有用于充油电气设备故障诊断的神经网络方法仅给出确定的故障诊断结果,不能给出诊断结果的可靠性。
为了解决这个问题,现借助神经网络理论指出即使针对同一组训练样本,不同初始权值和阈值、训练算法和网络结构下输出结果存在波动性,波动性的大小与网络输出的可靠性有关,多个网络输出的均值具有更小的误差,采用对3次多项式的逼近演示了该规律。基于确定的175个典型特征气体样本,基于自适应修正网络结构的方式,采用多种典型算法训练神经网络,针对每种算法训练成功获得10个多层前馈神经网络,然后采用训练得到的40个神经网络针对191个样本进行故障诊断,验证本文方法的有效性。
1 油色谱故障及诊断方法
1.1 油色谱故障诊断基础
充油电气设备在承受正常和过电压下容易发生不同程度的过热故障和不同类型的放电故障,过热和放电导致绝缘油和纸分解产生故障特征气体,特征气体逐渐溶解于油中,随着油循环逐渐扩散到其他区域,通过取油样口获得油样后根据振荡脱气等方式获得油中溶解的混合气体,通过气相色谱方式把故障特征气体进行分离,最后通过传感器检测气体浓度。由于故障类型和严重程度不同时油的产气类型和速度不同[20],这样根据测量得到特征气体的类型和浓度即可判断故障类型。较之其他充油电气设备的故障诊断方法,基于油色谱的诊断方法具有以下优势。
(1)非侵入式,常规方式无需在设备内安装传感器。
(2)便于在线监测,取油样时无需要求设备停电。
(3)适合于对早期故障的监测,早期的故障虽然不是很严重,但往往会使油中产生特征气体,通过离线或在线检测特征气体就能实现对故障的早期预警。
1.2 油色谱故障诊断方法
由于键能越大则分解需要的能量就越大,因此,产生烃类气体的不饱和度随裂解能量密度即温度的增加而增加[2]。根据热力动力学模拟产生哈斯特曲线可知,随着温度的升高,C2H2、C2H4和H2的分压比逐渐升高,CH4和C2H6的分压比逐渐下降。这样根据特征气体的类型、浓度和比例就可以诊断充油电气设备的故障,其中特征气体法诊断规则如表1所示。

表1 特征气体浓度与充油电气设备内部故障的关系
为了避免特征气体法缺乏量化的不足,人们还提出了各种比值法,具体介绍可参考文献[2]。
2 人工神经网络诊断及可靠性
2.1 多层前馈神经网络及训练算法
人工神经网络是一种模仿动物神经网络特征,进行分布式并行信息处理的算法模型,最为典型的多层前馈神经网络的结构如图1所示。
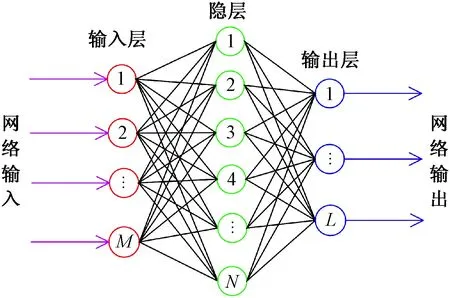
图1 多层前馈神经网络结构Fig.1 Structure of multilayer feedforward neural network
从数学角度上可以将多层前馈神经网络认为是一个映射。设一个单隐层的多层前馈神经网络输入层、隐层和输出层神经元数量分别为M、N和L,则该映射用数学方式表示如下:

(1)
式(1)中:ω1ij和ω2jl分别为输入层第i个神经元到隐层第j个神经元和隐层第j个神经元到输出层第l个神经元的权值;φ1和φ2分别为隐层和输出层神经元的激活函数;θi为隐层第i个神经元的阈值;[x1n,x2n, …,xMn]为第n个样本的输入数组;Fl为输出层第l个神经元针对第n个样本的输出。
涉及充油电气设备故障诊断时就是实现从输入特征气体浓度或比例到故障类型的映射。由于理论上多层前馈神经网络具有逼近任意复杂映射的能力,因此它在充油电气设备故障诊断中应用最为广泛。一般来说,隐层数量越多,隐层神经元数量越多,则网络的逼近(学习)能力就越强,但网络的泛化能力就越差,会影响诊断的准确性。所以隐层数量和隐层神经元数量应该在满足训练误差的要求下取最小值。而输入层和输出层神经元数量分别由特征气体数量和故障类型数量决定。一旦网络结构确定,剩下的关键问题就是采用优化算法调节神经网络中的权值和阈值,使针对训练样本输出结果的误差小于一定值。网络训练目标从数学角度来说就是让式(2)趋于最小化。
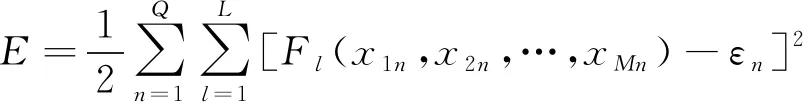
(2)
式(2)中:Q为训练样本数量;εln为针对第n个样本神经网络输出层第l个神经元输出的目标值。
其本质上是一个非线性最小二乘问题,常规的反向传播(back propagation,BP)算法采用误差的一阶梯度来修正网络的权值和阈值[19]。设神经网络可调变量有K个,网络可调变量的调整公式如式(3)所示。
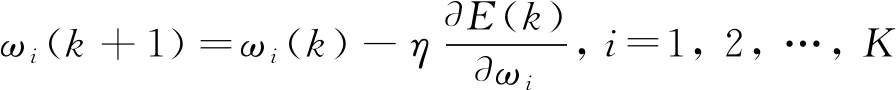
(3)
式(3)中:ωi为神经网络第i个可调变量;k为迭代次数;η为学习步长。注意,ωi与式(1)中的ω1ij和ω2jk构成相同的变量,即它们分别都构成神经网络的权值和阈值,只是为了表述方便,将下标进行调整。
常规的BP算法计算速度慢、容易陷入局部极小点,为了提高学习能力则要求增加隐层神经元数量,这容易使神经网络诊断的准确性下降。为了解决这一问题,提出了多种改进算法,典型的有RPROP算法[18]、共轭梯度法[21]以及基于二阶梯度的拟牛顿法[21]和列文伯格-马夸尔特法(Levenberg-Marquardt, LM)算法[17]。
采用RPROP算法[18]时,网络可调变量的调整公式为
ωi(k+1)=ωi(k)+Δωi(k),i=1, 2, …,K
(4)
式(4)中:Δωi为第i个可调变量的增量,可表示为
Δωi(k)=
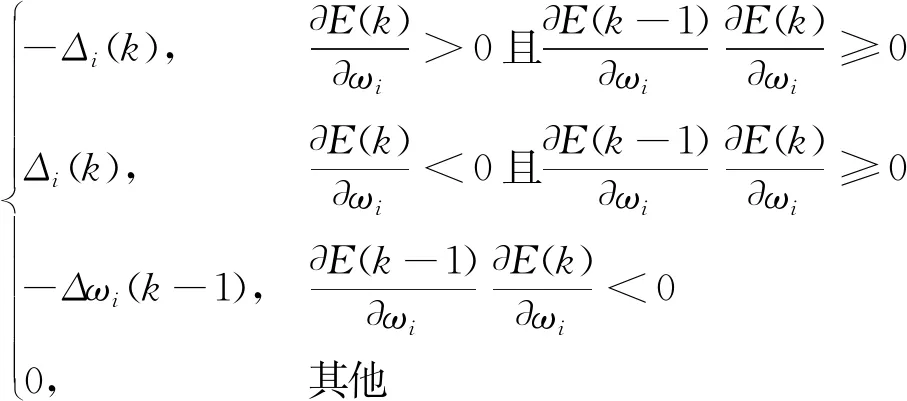
(5)
Δi(k)=
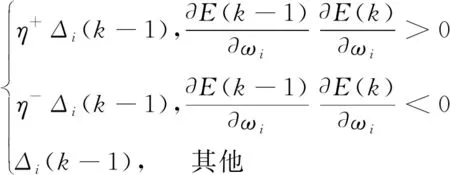
(6)
采用共轭梯度法[21]训练时神经网络可调变量增量的调整公式为
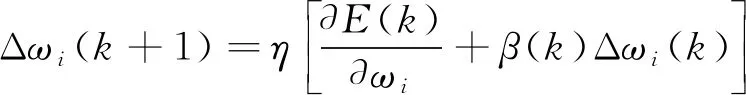
(7)
式(7)中:β为共轭因子,表示为
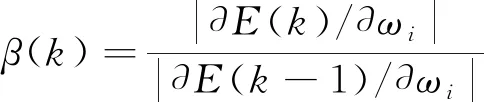
(8)
采用拟牛顿法[21]训练时神经网络可调变量的调整公式为
W(k+1)=W(k)-H(k)-1G(k)
(9)
式(9)中:G为梯度向量,G=[G1,G2, …,GK]T;H为K×K的Hessian矩阵,Hij为其第i行、第j列元素;W为神经网络变量(权值和阈值)构成的列向量,W=[ω1,ω2, …,ωK]。Gi和Hij表示为
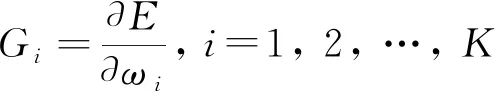
(10)

(11)
为了防止步长调整过大,引入可变参数λ,LM算法网络可调变量的调整公式为
W(k+1)=W(k)-(JTJ+λI)-1JTe[W(k)]
(12)
式(12)中:e为神经网络输出误差列向量,考虑到样本数量为Q,则其元素数量为QL,e=[e1,e2, …,eSL]T;I为K阶单位矩阵;J为Jacobian矩阵,Jij为其第i行、第j列元素,表示为
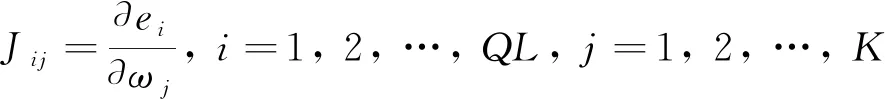
(13)
2.2 神经网络输出的可靠性
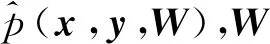
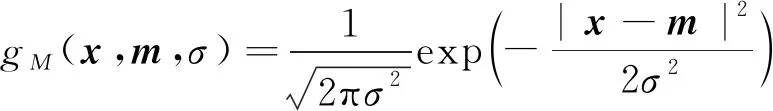
(14)
式(14)中:σ为标准差;m为与x维数一样的向量。
如果采用该网络对函数进行逼近[19, 22],则有

(15)
式(15)中:φ(x,W)为待逼近的真实函数;p(x)为输入样本出现的概率密度。
网络输出的均值和方差[19]分别为
E(x,W)=φ(x,W)
(16)
V(x,W)=Lσ2
(17)
可见,输出是给定输入下的条件均值,采用同样训练集训练得到不同神经网络输出的均值作为最终的输出能减少神经网络的误差。神经网络输出(诊断结果)的可靠性可以用不同神经网络输出结果的方差来衡量,方差越大则可靠性越低。这也容易理解,对于出现概率p(x)大的样本,由于附近可用于学习的样本数量多,不同实现方式下神经网络针对同一个样本计算得到网络的输出结果会非常接近,这时输出结果的可靠性也较高;对于出现概率p(x)小的样本,由于可用于学习的样本数量少,随机性就偏大,输出结果可靠性偏低。
以上的同样训练集训练得到不同神经网络可以采用不同训练算法、隐层神经元数量、初始权值和阈值的多层前馈神经网络训练获得。
下面以不同初始权值和阈值的多层前馈神经网络对3次多项式的学习效果来验证以上分析。根据[x,y],y=x3,x=-3, -2.9, …, -1.8, 1.8, 1.9, …, 3对神经网络进行训练。神经网络隐层神经元数量为3,利用RPROP算法训练,不同权值和阈值下训练得到10个神经网络。3次多项式、神经网络的训练样本,训练后网络输出结果及10个神经网络输出结果的均值如图2所示。由图2可知,对于训练样本密集的-3≤x≤-1.8和1.8≤x≤3范围内训练得到不同神经网络的输出非常接近,而对于没有训练样本的-1.8≤x≤1.8范围内多个神经网络的输出差别较大,这也就意味着输出的标准差较大,而此时的输出准确性偏低,实际上不同训练算法也有类似的结果。这也验证了根据不同训练算法、隐层神经元数量、初始权值和阈值训练得到多个网络的输出的标准差可以判断网络输出结果的可靠性。另外,10个网络输出结果的均值更加接近准确值,这也为后续减少诊断误差指明了方向。
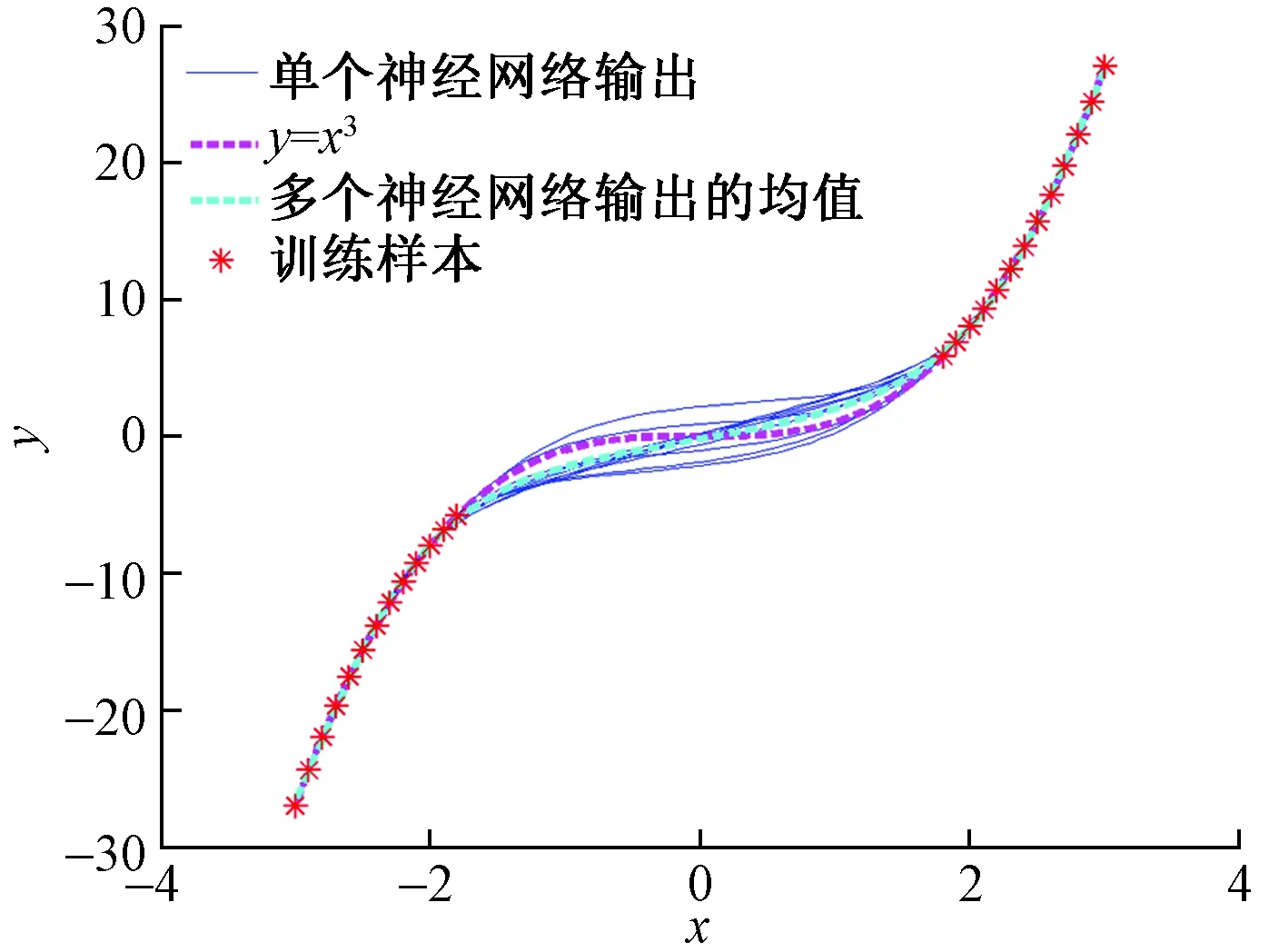
图2 神经网络对y=x3的拟合效果Fig.2 Fitting results of y=x3 by ANNs
3 神经网络及训练
3.1 油色谱样本
从现有文献中选择典型的175组故障特征气体作为训练样本,另外的191组样本作为测试样本,两类样本的统计如表2所示。由于公开发表文献中低温过热故障偏少,所以用于训练和测试的样本中该类型故障的样本也偏少。

表2 不同故障类型的训练和测试样本数量
3.2 神经网络结构
由于故障诊断用的特征气体分别为H2、CH4、C2H6、C2H4和C2H2,故输入神经元数量为6。输出为6种类型故障,即低温过热、中温过热、高温过热、局部放电、火花放电和电弧放电;故输出层神经元数量也为6。考虑到训练样本的数量以及分布,同时考虑到训练算法的性能以及为了使训练得到的神经网络具有更好的诊断准确性,努力压缩隐层神经元的数量和个数,经过不断尝试隐层数量选择1,隐层神经元数量选择18~22。隐层和输出层神经元的激活函数分别为sigmoid函数和线性函数。考虑到实际情况下特征气体浓度可能会在很大范围内变化,故用于训练的输入数据为每种气体浓度与总气体浓度的比值。对于输出结果,如果属于该类故障则对应的神经元应该输出为1,其他神经元应该输出为0。
3.3 训练结果
训练目标的均方误差为0.01,采用自适应修正网络结构方式,即初始隐层神经元数量为18,如果5次训练仍不收敛,则隐层神经元数量加1,直至满足训练目标。如果隐层神经元数量大于22,则设置初始隐层初始神经元数量为18后重新开始计算,重复直至训练得到满足要求的神经网络。最后针对4种算法成功训练得到10个神经网络。
4种训练算法的均方误差随迭代次数的变化如图3所示。针对每种类型的训练样本,每种训练算法得到10个神经网络诊断准确性的均值如表3所示。除了低温过热样本诊断准确性略低外,其他故障诊断准确性足够高,这表明训练得到网络较好地学习到了训练样本中隐含的故障诊断规则。注意,输出层6个神经元的输出中,与1最为接近神经元的输出被诊断为该神经元对应的故障。表4所示为针对所有训练样本,4种训练算法得到神经网络诊断准确性的均值和10个神经网络输出均值对应的故障诊断准确性。由表4可知,不同算法训练得到网络诊断准确性的平均值比较接近,基本在97.66%~98.4%范围内变化。通过对10个神经网络的输出取平均值,诊断的准确性得到了提高,达到了98.86%~100%,4种算法训练得到神经网络的诊断准确性也比较接近。对10个网络输出求平均后,诊断的准确性提高了0.91%~1.89%,均值为1.26%。以上结果有效验证了采用同样训练集,不同权值和阈值、网络结构训练得到不同神经网络输出的均值作为最终的输出能减少神经网络的诊断误差。
以上4种算法成功训练完成一个神经网络需要的时间分别为137.52、718.44、127.32、113.15 s。由此可见,RPROP算法、拟牛顿法和LM算法的训练时间非常接近,而共轭梯度法的训练时间为其他3种算法的6倍左右。
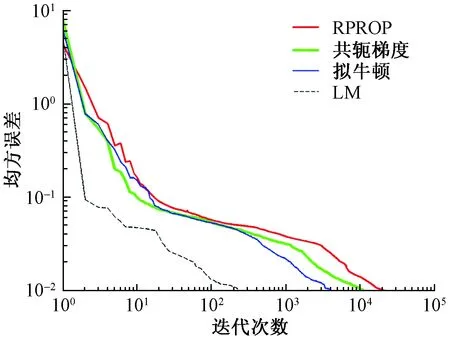
图3 训练误差与迭代次数的关系Fig.3 Change of error with iteration number
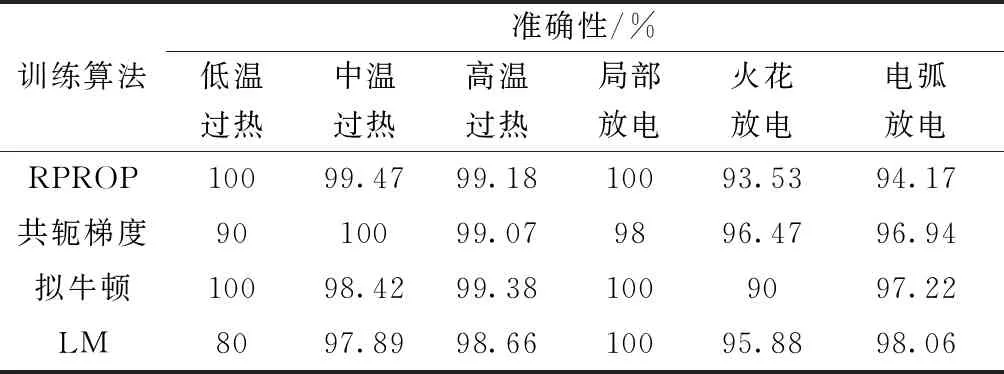
表3 采用不同算法得到神经网络针对训练样本的故障诊断准确性
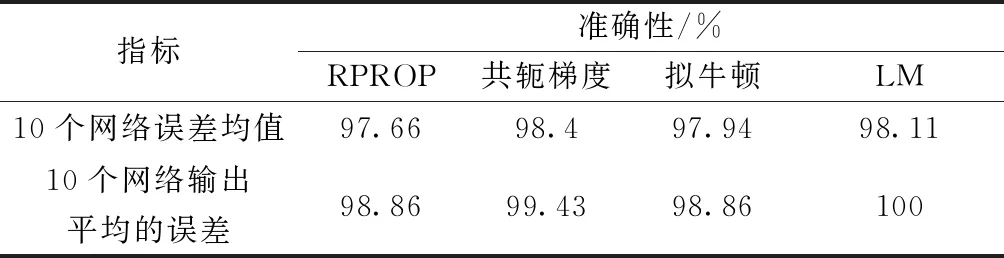
表4 常规神经网络方法和本文提出神经网络方法针对训练样本的故障诊断准确性
4 实际案例验证
经过尝试采用式(18)来实现神经网络输出(诊断结果)可靠性指标R的计算,该指标越接近于1,则诊断结果的可靠性越高。
R=exp(-2σ1)
(18)
式(18)中:σ1为输出结果的标准差。
对于每种算法训练完成的10个神经网络,针对测试样本诊断准确性均值如表5所示,把10个神经网络的输出结果求平均得到不同训练算法对应网络诊断准确性以及10个神经网络诊断准确性的均值如表6所示。表5中对于低温过热故障各种算法训练得到网络的诊断准确性均不高,这是因为低温过热故障的样本较少,训练样本过少不能有效学习到对应的诊断规则。对于局部放电和火花放电网络的诊断准确性也不是很高,这可能是因为这些故障对应的训练样本不能对理论(测试)样本空间进行很好的覆盖,导致训练得到的神经网络不能有效学习到故障诊断规则所致。随着后期有效的训练样本的增加,故障诊断的准确性有望进一步提高。
由表6可知,不同算法训练得到网络诊断准确性的平均值比较接近,基本在86.81%~89.21%范围内变化。通过对10个神经网络的输出取平均值,诊断的准确性得到了提高,达到了88.48%~92.15%。即对输出求平均后诊断的准确性提高了1.68%~3.82%,均值为2.57%。以上结果有效验证了第2节提到的采用同样训练集训练得到不同神经网络输出的均值作为最终的输出能减少神经网络的诊断误差。
下面用2个典型测试样本及结果进一步展示本文方法的效果。2个典型样本的故障特征气体浓度如表7所示,样本1[23]是针对辽宁某发电厂1号主变压器型号为SFPS-120000/220的油色谱数据,样本2[22]为针对直属某电厂500/220 kV联络变压器,C相,型号为ODFPSZ-120000/500的油色谱数据。其中样本1多个神经网络的诊断结果一致,为诊断可靠性较高的情况;样本2为多个神经网络输出结果差别较大,半数及以上神经网络出现误诊断的情况,为单一神经网络诊断可靠性较低的情况。样本1和样本2典型测试样本网络输出的范围、均值、标准差和诊断结果的可靠性分别如表8和表9所示。
由表8可知,4种算法训练得到神经网络均诊断为火花放电,且可靠性指标接近于1,故障诊断的可靠性较高。这表明神经网络有效学习到了针对该样本的故障诊断规则,多种情况下诊断结果能互相验证,诊断可靠性高,这与本文方法的诊断结果吻合。实际吊罩检查结果为66 kV一套管均压球松动,并有放电痕迹,均压球内有大量游离碳[22],神经网络的故障诊断结果与实际结果基本吻合。对于样本2,不同训练算法、初值权值和阈值、结构下训练得到网络的诊断结果有低温过热、中温过热、高温过热、局部放电、火花放电和电弧放电,另外多个网络输出结果标准差整体偏大,多个故障类型对应的可靠性指标偏低,这能很好地给用户警示,说明此时各个神经网络诊断结果的可靠性偏低。而对各种算法训练得到的10个神经网络的输出取平均值后得到的故障诊断结果均为火花放电。实际吊罩检查结果为均压球与导管接触不良,造成导管与均压球之间产生悬浮电位放电,球内积存了大量游离碳[22],神经网络诊断结果与实际情况能基本吻合。
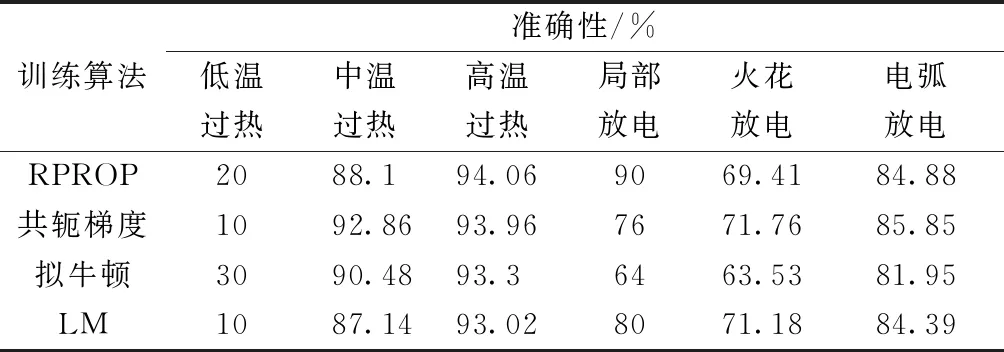
表5 采用不同算法得到神经网络针对测试样本的故障诊断准确性
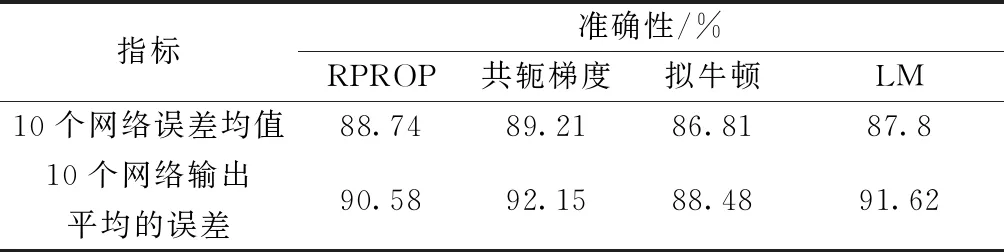
表6 常规神经网络方法和本文提出神经网络方法针对训练样本的故障诊断准确性

表7 2个典型测试样本的特征气体浓度
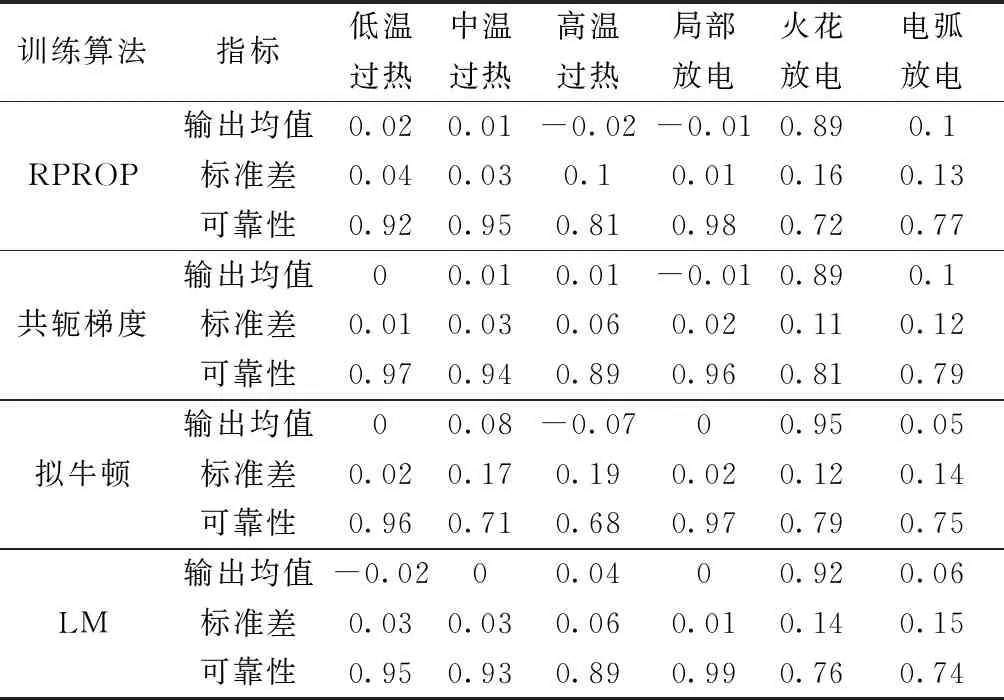
表8 样本1的网络输出、标准差及对应的可靠性
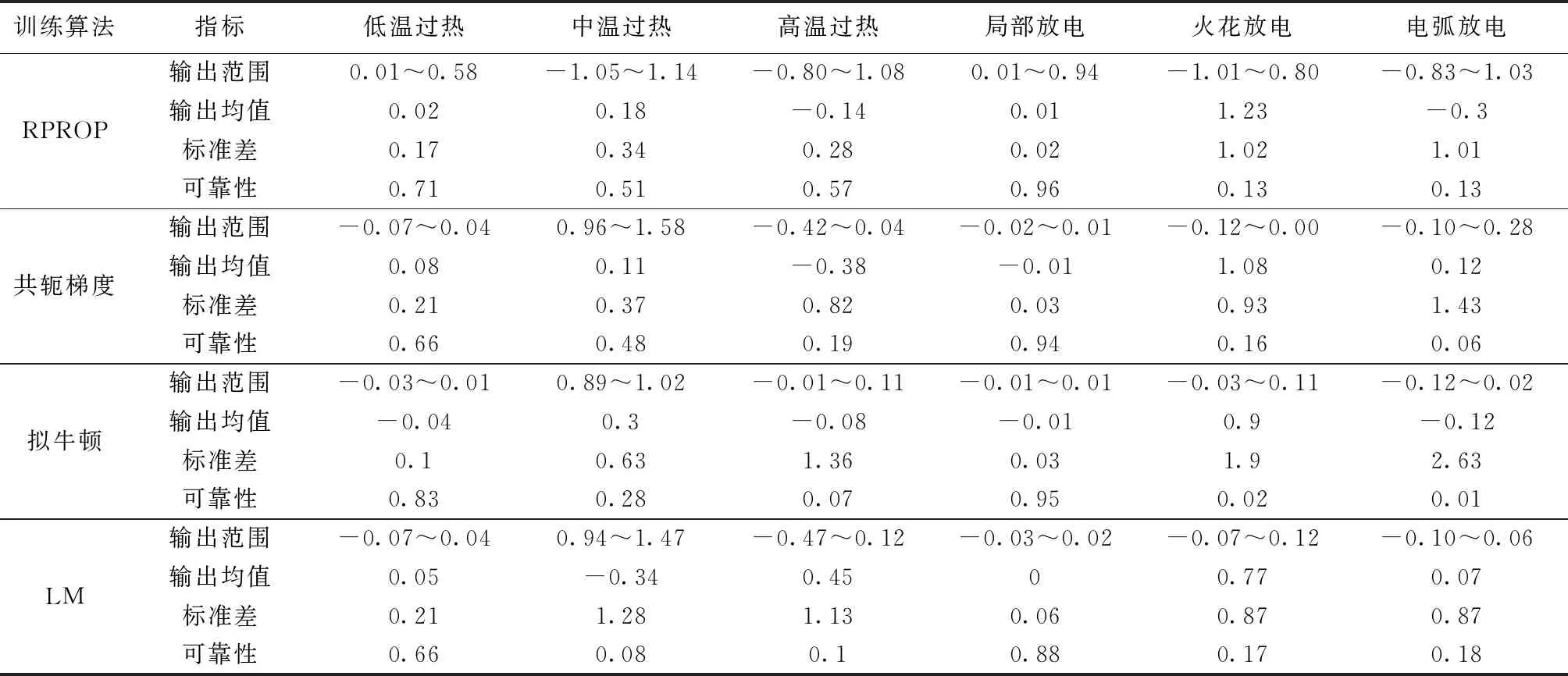
表9 样本2的网络输出、标准差及对应的可靠性Table 9 Output and standard deviation, fault diagnosis reliability of ANNs for the second sample
5 结论
根据搜集得到的大量油色谱样本,分别采用RPROP算法、共轭梯度法、拟牛顿法和LM算法针对不同权值和阈值、网络结构训练多个神经网络,将训练得到神经网络应用于基于油色谱的充油电气设备故障诊断,得到的结论如下。
(1)神经网络结构相似时,4种算法训练得到的神经网络具有相近的故障诊断准确性,但从训练时间上看,RPROP算法、拟牛顿法和LM算法非常接近,而共轭梯度法的训练时间为其他3种算法的6倍左右。
(2)使用不同网络结构、训练算法、初始权值和阈值训练得到神经网络输出结果的标准差可以获得诊断结果的可靠性,为神经网络诊断提供了另外一个维度的信息。
(3)将不同网络结构、训练算法、初始权值和阈值训练得到神经网络输出结果的均值作为诊断结果可以提高诊断的准确性。
