AMT 换挡滑块的磨损量预测与磨损规律数值分析
2021-10-16刘雨薇孙园植王叶付崇智陈浩李秀明
刘雨薇,孙园植,王叶,付崇智,陈浩,李秀明
(1.中国矿业大学(北京) 机电与信息工程学院,北京 100083;2.中国北方车辆研究所,北京 100072)
同步器是电控机械式自动变速箱(AMT)的关键部件,同步器的使用降低了汽车换挡的操控难度,并大大延长了变速箱的使用寿命[1]。随着对换挡品质要求的提高,AMT 中同步器磨损失效的问题受到越来越广泛的关注。
磨损失效的同步器会导致汽车在挂挡时出现打齿或挂不上挡等现象,直接影响驾驶者的换挡感受,甚至会危害驾驶安全[2-4]。同步器的磨损研究多侧重于同步环磨损和润滑性能[5-9]。王炎等[10]通过对同步器工作过程进行仿真,预测了同步器锥面的磨损寿命。苏洪[11]利用RBF 神经网络分析了摩擦锥面的部分参数对磨损的影响。BROWN 等[12]的研究结果表明,润滑添加剂对同步器的摩擦磨损性能有重要影响。在使用过程中,同步器除了锥面发生磨损失效外,换挡滑块的早期异常磨损将严重影响换挡功能,但目前对于换挡滑块的磨损研究并不多见。文昊等[13]的研究结果表明,同步器磨损失效过程中,换挡滑块与接合套间的磨损使所需换挡行程加大,接合套难以压紧同步环,导致无法完成同步,同时加剧了同步环与锥体间的磨损。安海等[14]通过滑块磨损试验,采用偏最小二乘法拟合出磨损量关于换挡力、转速和硬度的预测方程,并对不同类型的变量进行了分析,得到了滑块磨损混合的可靠性模型。磨损量指由于磨损引起的材料损失量,可通过测量长度、体积或质量的变化而得到,并相应地称它们为线磨损量、体积磨损量和质量磨损量。本文研究的对象为换挡滑块在单次换挡过程中的单侧线磨损量,即为磨损深度。下文中将“线磨损量(line wear)”统称为“磨损量(wear)”。现有的文献多采用台架试验或实车试验的方法[15],这些传统的试验方式成本高,效率低,且磨损量预测模型误差较大。本文采用仿真试验代替传统试验,根据BOX设计方法,对不同换档力、接合套转速、摩擦系数作用下的换挡滑块磨损量进行数值模拟,探究其对滑块磨损量的影响机制,并且建立了换挡滑块磨损量的预测优化模型。研究结果将为后续优化换挡控制策略奠定基础,对提高AMT 的换挡品质具有重要意义。
1 换挡滑块磨损特性数值分析
1.1 有限元模型
从AMT 三维几何模型中提取出换挡滑块与接合套,见图1。为研究滑块的单侧磨损量,按对称结构建立1/2 模型,提高仿真效率。滑块的硬度较低,换挡过程中磨损严重,因此可将滑块作为变形体,接合套作为刚体来简化有限元模型,见图2。滑块与接合套刚体建立接触对,并在滑块对面建立固定约束。设定刚体接合套控制节点的旋转速度,并施加相应的换挡力。在相同的边界条件下,全柔体模型与刚柔耦合模型的计算结果差异不超过10%。因此,采用刚柔耦合模型计算能够较为准确地反映其磨损特性,并且计算效率较高。
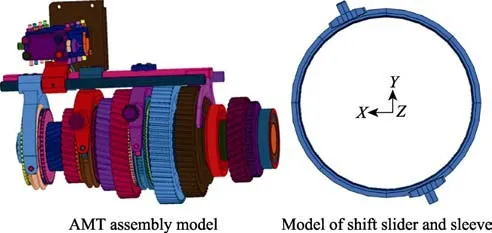
图1 AMT 三维模型Fig.1 Three-dimensional model of AMT
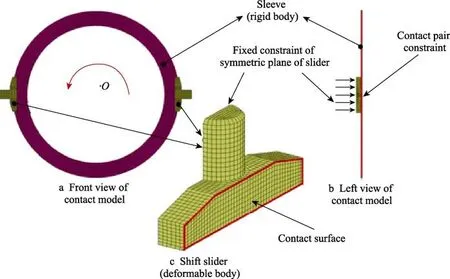
图2 滑块与接合套刚柔耦合接触模型Fig.2 Rigid-flexible coupling contact model between the shift slider and the sleeve
1.2 材料性能与工况参数
在运动过程中,摩擦副接触面上产生大量的摩擦热,并且伴随着磨损现象的发生。材料的热物性对其机械性能与摩擦性能具有较大影响,不同材料间的摩擦所产生的磨损现象也不相同。换挡滑块材料为铜合金CW713R-H140,接合套材料为45#钢,二者的热物性参数见表1。此外,换挡滑块与接合套摩擦过程中,滑块的磨损类型以粘着磨损为主。在寿命周期内,滑块的磨损主要处于稳定磨损阶段,磨损率保持不变,采用Archard 磨损模型计算磨损量,磨损系数取k= 0.0017。

表1 接触材料的热物性参数Tab.1 Thermophysical parameters of the contact material
当滑块产生塑性变形时,磨损深度w与滑块接触面的法向载荷Fa、滑块的屈服极限σy、滑动距离L之间的关系如公式(1)所示。

设定接合套旋转控制点为接合套模型的中心点,接合套以控制点为旋转中心,垂直接合套平面坐标轴为旋转轴。
参照实际情况,在工作过程中,AMT 周围的环境温度为90 ℃。在换挡过程中,换挡力的变化范围为400~1000 N,挡位转速的变化范围为1000~2000 r/min,换挡时间为0.5 s,在无润滑的滑摩条件下,钢与铜合金的摩擦系数为0.15~0.25[13,16-17]。
实际换挡过程中,接合套的转速并非恒定为挡位转速,而是存在一定波动。为提高仿真结果的准确性以及仿真过程的效率,将接合套的转速变化规律简化为线性变化。考虑到仿真结果的可靠性,以挡位转速为2000 r/min、摩擦系数为0.15、换挡力为700 N 为例,对转速变化程度进行了多种方案的对比,结果见表2。

表2 不同转速波动下的仿真结果Tab.2 Simulation results under different speed fluctuation
在仿真误差的允许范围内,通过对同一绝对值的转速波动的仿真结果取均值,近似代替恒定转速下的仿真结果。通过对比可知,在允许的误差范围内,该假设条件下的仿真结果是可靠的。为了简化后续的仿真过程,选取图3 中的转速波动曲线作为有限元模型中的速度曲线,由此得到的磨损量偏差最小。
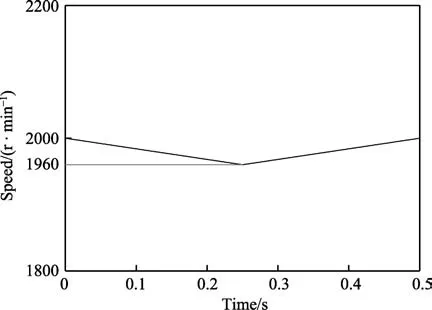
图3 转速波动下降2%的转速曲线Fig.3 Speed curve with 2% reduction in speed fluctuation
1.3 换挡滑块的热边界条件
1.3.1 换挡滑块的接触热导
在换挡滑块与接合套的实际接触过程中,接触表面不是光滑表面。热量在接触面间传递时,由于接触面积缩小而形成的额外换热阻力称为接触热阻,热流密度与固体界面温差的比值称为接触热导,两者互为倒数[18]。在对摩擦副进行热分析时,绝大部分文献采用了静态下的接触热阻模型[19-22]。与此不同,本文考虑了换挡滑块与接合套在滑摩过程中,其相对运动形式对接触界面传热特性的影响。
采用本文作者[23-24]所提出的双粗糙滑动表面间的有效接触热阻模型,其中接触热导值取决于外加载荷、界面初始温度、表面粗糙度、滑动速度等因素,即:
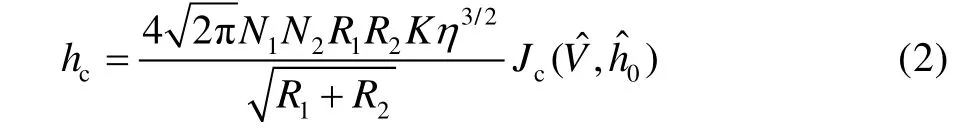
其中,
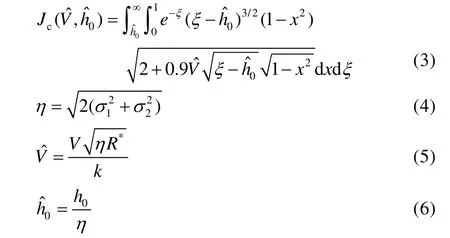
式中:Ni为平面i上单位面积的微凸体峰顶个数,Ri为平面i上单位面积上的微凸体的半径,K为导热率,无量纲滑动速度为Peclet 数,V为两个粗糙表面间的相对滑动速度,R*为微凸体的复合半径,h0为两个参考平面间的距离。
对于完全相同的两个表面,有:


1.3.2 换挡滑块的对流换热系数
换挡过程中,换挡滑块与接合套间的摩擦会产生大量的摩擦热。摩擦热以热传导的方式不断传递到换挡滑块,致使换挡滑块的温度上升,与周围环境形成了温差,换挡滑块还会与周围的环境介质发生对流换热。
根据流体有无相变,对流换热可以分为相变换热和无相变换热,本文主要研究无相变换热。工程上通常以Gr/Re2的值来判定对流换热方式,其中Gr为格拉晓夫数,Re为雷诺数。其判断标准见表3。

表3 对流换热方式的判断标准Tab.3 Judgment criteria of convective heat transfer modes
雷诺数Re的计算公式为:

式中:v为空气相对运动速度,m/s;l为换热表面的特征长度,m;ηair为空气常温下的运动黏度,m2/s。
在对换挡滑块的换挡过程进行数值分析时,假设换挡滑块固定不动、接合套旋转,接合套的转速等于实际换挡过程中变速箱齿轮的转速。在此过程中,换挡滑块与周围空气没有发生相对运动,即v=0 。因此,雷诺数Re为0,由表3 判断换挡滑块与周围空气的换热方式为自然对流换热。
对流换热系数hcon的计算公式为:

式中:Nu为努塞尔数;λair为空气导热系数,W/(m ·K) 。
在计算换挡滑块的自然对流换热系数过程中,首先需计算相关参数。
自然对流换热下,努塞尔数Nu的计算公式为:
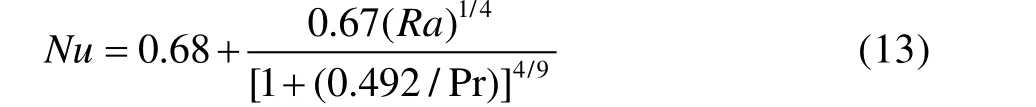
式中:Ra为瑞利数;Pr为普朗特数。
瑞利数Ra的计算公式为:

普朗特数Pr的计算公式为:

格拉晓夫数Gr的计算公式为:

经计算得,格拉晓夫数Gr为730.17,普朗特数Pr为0.7032,瑞利数Ra为513.41,努塞尔数Nu为3.1995。将努塞尔数Nu与空气导热系数λair和换热表面特征长度l代入式(12),算得换挡滑块的自然对流换热系数hcon为 2.13 W/(m2· K)。
1.3.3 接合套的对流换热系数
假设接合套的转速等于实际换挡过程中变速箱齿轮的转速。假定接合套转速为最低挡速ln=1000 r/min,此时空气的相对运动速度为:

式中:r0为接合套与换挡滑块接触表面的中径,r0= 0.086 m 。
经计算,此时空气的相对运动速度v为8.9875 m/s。代入式(11),得到雷诺数Re为2732.7。由式(16)计算得,格拉晓夫数Gr为1.1457,则Gr/Re2=1.53 ×10-7。由表3 判断接合套与周围空气的换热方式为强迫对流换热。当接合套转速增加时,空气的相对运动速度增大,雷诺数Re增大,Gr/Re2的值减小。因此,接合套的对流换热方式始终为强迫对流换热。
强迫对流换热下,努塞尔数Nu的计算公式为:

式中:C′为常数,取0.683。
接合套的换热表面特征长度为4.5 mm,由式(15)计算得,普朗特数Pr为0.7032。在不同转速下,计算强迫对流换热下的雷诺数、努塞尔数和对流换热系数,计算结果见表4。

表4 强迫对流换热下的Re、Nu 和hconTab.4 Re, Nu, and hcon under forced convection heat transfer
1.4 仿真试验设计方案与结果
采用有限元仿真试验的方法代替传统试验,针对换挡滑块磨损量预测的需求,选用响应面设计试验方法中的BOX 设计方法。该方法通过有限次试验所得的数据,在麦克劳林或泰勒展开式的基础上,估计响应面的回归方程系数,并利用回归方程估计极值点、定值点等,找出优化搭配。
基于Archard 磨损公式,滑块磨损量的影响因素有3 个,分别为转速(A)、摩擦系数(B)和换挡力(C)。根据BOX 设计方法,每个因素有3 个水平且分布均匀,对所需的17 个仿真试验点进行有限元仿真,得到磨损量的仿真结果,见图4 和表5。
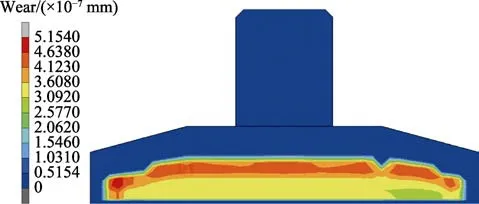
图4 磨损量的有限元仿真结果Fig.4 Finite element simulation results of wear
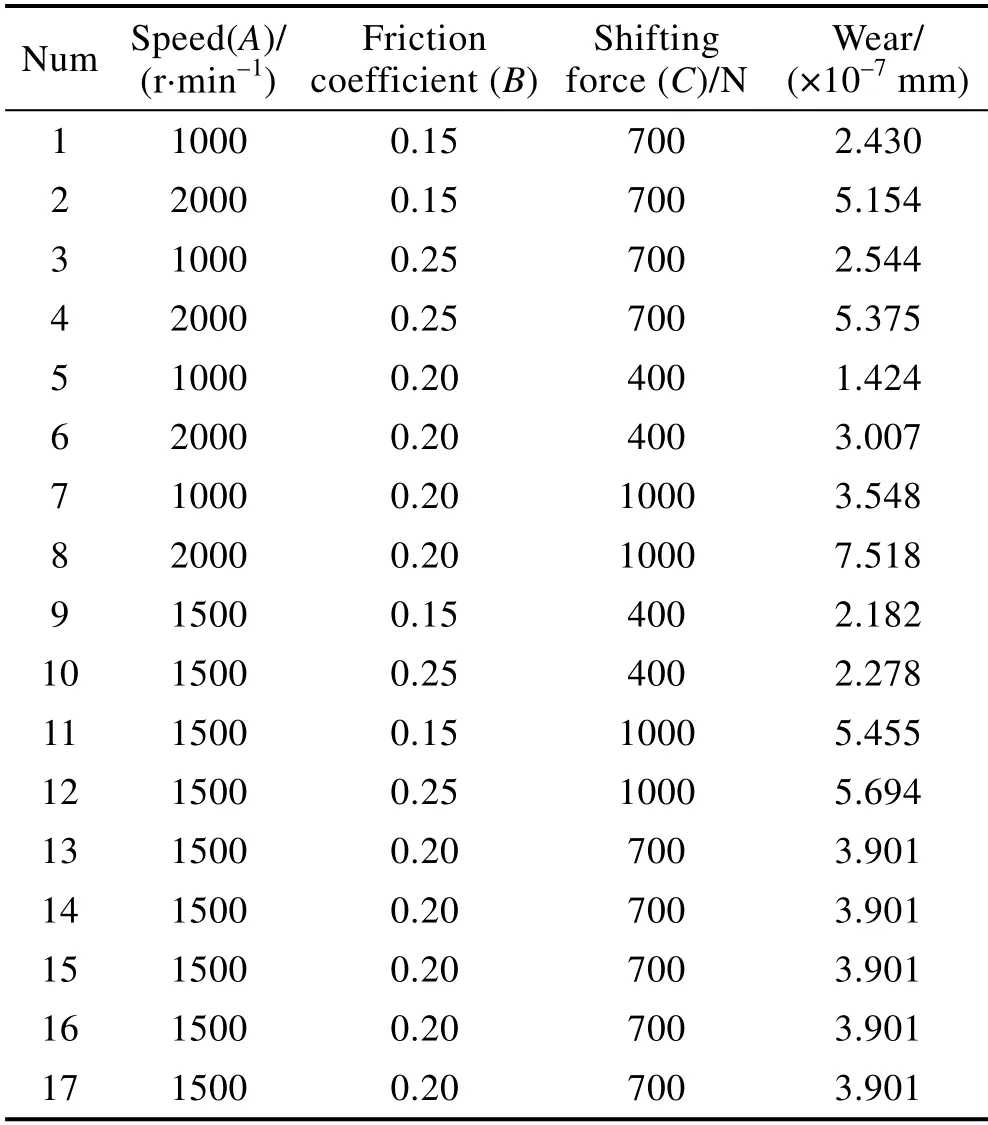
表5 换挡滑块磨损量的仿真结果Tab.5 Simulation results of wear of shift slider
2 换挡滑块磨损量的预测优化模型
2.1 预测优化模型的建立
通过BOX 响应面分析方法对仿真试验结果进行处理,建立磨损量模型。在各采样点上,通过方差分析确定各因素对磨损量影响的显著程度,在此基础上,采用Stepwise 模型消除不显著项,模型F值为63 660 000.00。在F检验中,P值表示显著性水平,P≤ 0.05的项可认为是显著项,P≤ 0.01的项可认为是极其显著项。通过对P值进行分析,模型中A、B、C、AB、AC、BC、A2、B2、C2、A2B、A2C、AB2是极其显著的模型项。模型对应的P值小于0.0001,说明模型对磨损量的影响极其显著。其中,一次项A、B、C对应的P值小于0.0001,说明转速(A)、摩擦系数(B)、换挡力(C)均为重要的影响因子。由此建立的滑块磨损预测模型如下式所示:
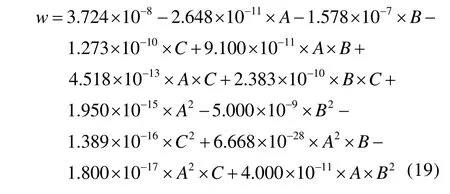
2.2 预测优化模型的准确性检验
将有限元仿真水平的组合值带入回归方程,将得到的磨损量预测值与仿真值进行对比,见表6。结果显示,回归方程对换挡滑块磨损量的预测值与有限元软件的仿真值误差不到万分之一。因此,可认为该回归方程能够准确地反映在以上水平组合的影响因素下,换挡滑块在换挡过程中的磨损量。
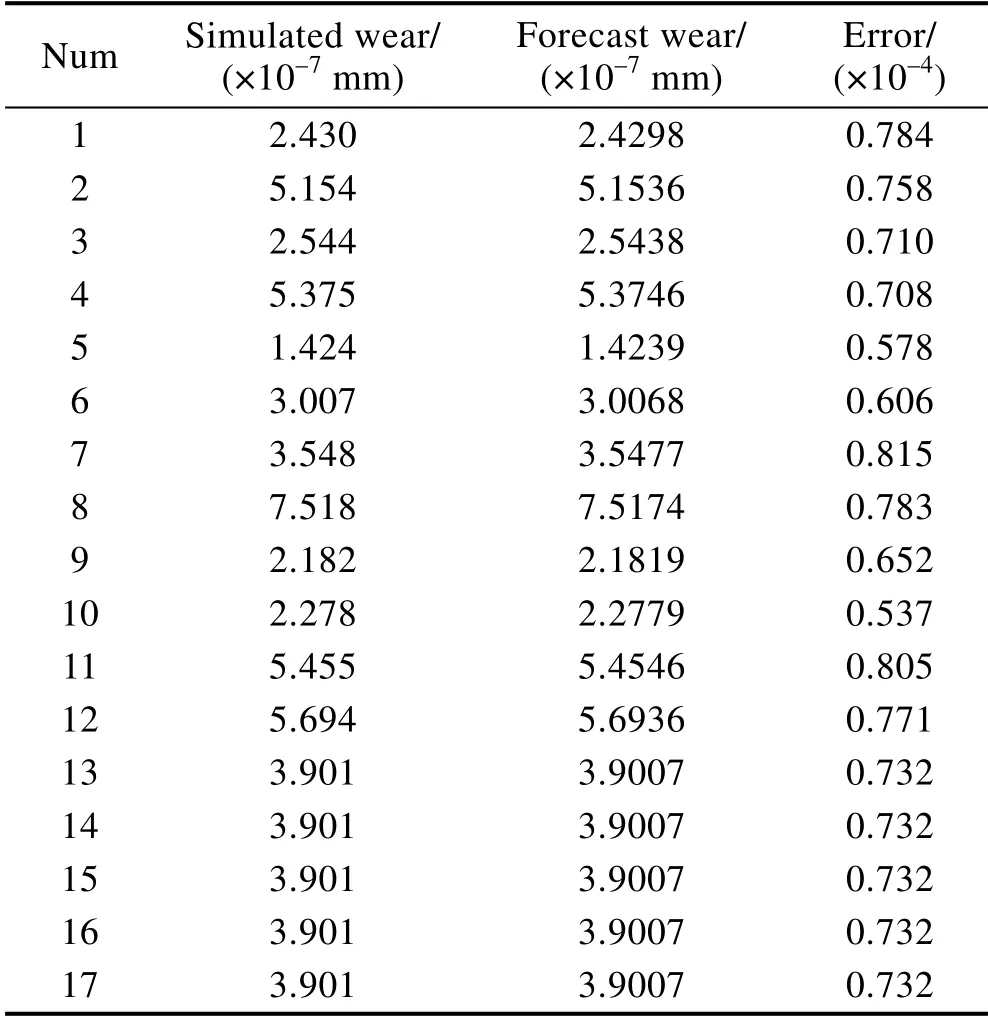
表6 回归方程预测值的验证表Tab.6 Verification table of the predicted values of the regression equation
通过设计影响因素的新水平组合来检验回归方程对换挡过程中换挡滑块磨损量的预测精度。在工况参数不变的条件下,将影响因素的新水平组合分别代入有限元软件进行仿真。同时,将新水平组合依次带入回归方程进行预测,得到换挡滑块磨损量的仿真值和预测值,见表7。

表7 回归方程预测精度的检验Tab.7 Test of prediction accuracy of regression equation
对比结果显示,回归方程计算的换挡滑块磨损量预测值与有限元软件的仿真值误差最大不超过8%,且对初始拟合水平组合内换挡滑块磨损量的预测误差不到1%。考虑不同挡位下接合套转速范围的不同,当转速为750~5000 r/min 时,随机设定接合套转速、摩擦系数和换挡力,将回归方程计算的换挡滑块磨损量的预测值与有限元软件的仿真值进行对比。结果表明,预测值与仿真值的最大误差不超过15%,且在绝大多数情况下低于10%。
2.3 预测优化模型与仿真模型的可靠性检验
通过试验验证预测优化模型与仿真模型的可靠性,将试验参数分别代入预测优化模型与仿真模型,并将预测磨损量、仿真磨损量与试验磨损量进行比较。试验模拟换挡滑块从3 挡到4 挡的过程,接合套转速为2200 r/min,摩擦系数为0.15,换挡力为816 N,换挡次数为45 025 次,试验后换挡滑块的单侧磨损量为0.03 mm。经计算,换挡滑块的平均单次换挡磨损量为 6.663 ×1 0-7mm。将试验参数代入预测优化模型与仿真模型,分别得到预测磨损量fR和仿真磨损量sR,见表8。通过计算得出预测磨损量、仿真磨损量与试验磨损量之间的误差,验证预测优化模型与仿真模型的可靠性,见表9。

表8 试验条件下的仿真磨损量和预测磨损量Tab.8 Simulated wear and forecast wear under the conditions of test

表9 仿真模型和预测优化模型与试验结果的对比检验Tab.9 Comparison results of simulation model and prediction model with test
结果显示,在转速为2200 r/min、摩擦系数为0.15、换挡力为816 N 的条件下,预测优化模型和仿真模型的误差均小于5%。因此,在一定误差范围内,预测优化模型可以准确预测换挡滑块在换挡过程中的磨损量。
3 各因素对磨损量的影响规律
3.1 转速、换挡力、摩擦系数对滑块磨损量的影响规律
图5—7 为不同参数条件下预测优化模型的磨损量变化曲线。其中,图5 为摩擦系数f=0.2,换挡力分别为400、700、1000 N,转速为750~5000 r/min时的磨损量变化曲线。

图5 f = 0.2 时不同换挡力下的磨损量-转速曲线Fig.5 The wear-speed curve under different shifting forces when f = 0.2
由图5 可知,在摩擦系数f和换挡力F一定的情况下,磨损量随转速的增大而增大,曲线的斜率随转速的增大略微减小,但在转速为1000~2000 r/min 时,斜率的变化并不明显,可近似看作一条直线。同时,曲线的斜率随换挡力F的增大而增大,变化较为显著。
由图6 和图7 可知,磨损量随摩擦系数f的增大而增大,且在图7 中发现,曲线的斜率随摩擦系数的增大略微增大。在所研究的水平范围内,摩擦系数对换挡滑块磨损量的影响小于换档力和转速对磨损量的影响。

图6 F = 700 N 时不同转速下的磨损量-摩擦系数曲线Fig.6 The curve of wear-friction coefficient under different speeds when F = 700 N
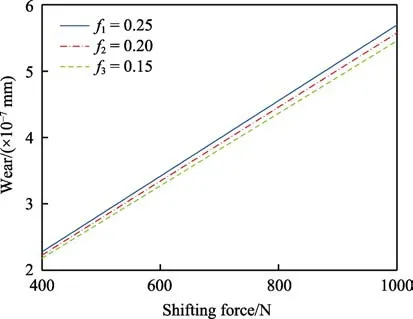
图7 ω = 1500 r/min 时不同摩擦系数下的磨损量-换挡力曲线Fig.7 The curve of wear- shifting force under different friction coefficients when ω = 1500 r/min
由图5 和图7 可知,在摩擦系数f和转速ω一定的情况下,磨损量随换挡力F的增大而增大,且在图5 中,曲线的斜率随换挡力F的增长,其增长趋势较为显著。
3.2 转速与换挡力的交互作用
换挡力F分别取400、700、1000 N 时,不同摩擦系数和不同转速对换挡滑块磨损量的响应面,如图8—10 所示。通过对滑块磨损量响应面的对比分析,可以验证上述关于转速ω、摩擦系数f、换挡力F对换挡滑块磨损量的影响规律。
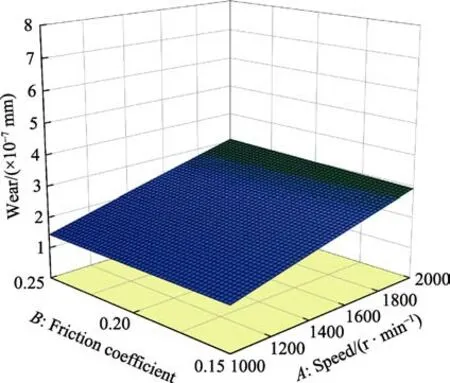
图8 换挡力为400 N 时摩擦系数和转速对磨损量的影响Fig.8 Influence of friction coefficients and speeds on wear under shifting force of 400 N
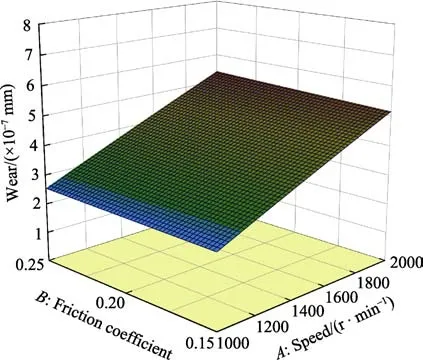
图9 换挡力为700 N 时摩擦系数和转速对磨损量的影响Fig.9 Influence of friction coefficients and speeds on wear under shifting force of 700 N
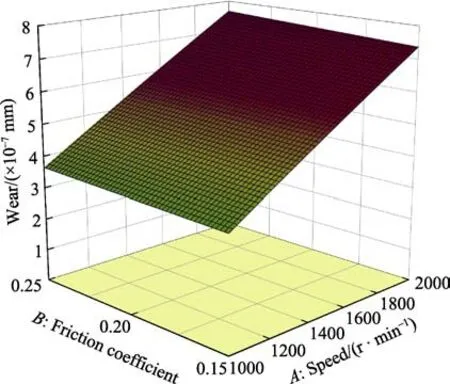
图10 换挡力为1000 N 时摩擦系数和转速对磨损量的影响Fig.10 Influence of friction coefficients and speeds on wear under shifting force of 1000 N
图11 为摩擦系数f为0.25 时,不同换挡力和不同转速对换挡滑块磨损量的响应。摩擦系数f一定时,随着换挡力F的增大,转速ω增大对磨损量的影响增大;随着转速ω的增大,换挡力F增大对磨损量的影响也增大。
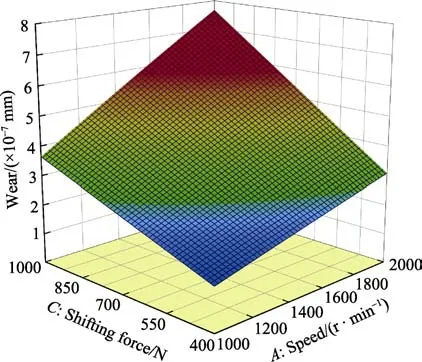
图11 f = 0.25 时换挡力和转速对磨损量的影响Fig.11 The influence of shifting forces and speeds on wear when f = 0.25
考虑3 个影响因素之间的交互性,分别在确定一个影响因素的水平值的前提下,作出另外两个水平值对磨损量影响的等高线图,见图12—14。由等高线图分析可知,在3 个影响因素中,转速ω和换挡力F对换挡滑块磨损量影响的交互作用最为显著,与图11 的响应面反映出的规律吻合。摩擦系数f与转速ω,或摩擦系数f与换挡力F对换挡滑块磨损量影响的交互作用较小。

图12 转速为1500 r/min 时换挡力和摩擦系数对磨损量影响的等高线图Fig.12 Contour map of the influence of shifting forces and friction coefficients on wear when the speed is 1500 r/min
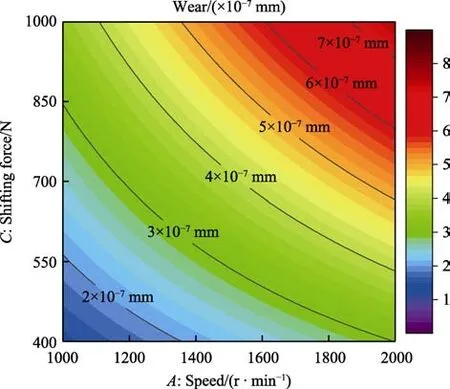
图13 摩擦系数为0.2 时换挡力和转速对磨损量影响的等高线图Fig.13 Contour map of the influence of shifting forces and speeds on wear when the friction coefficient is 0.2
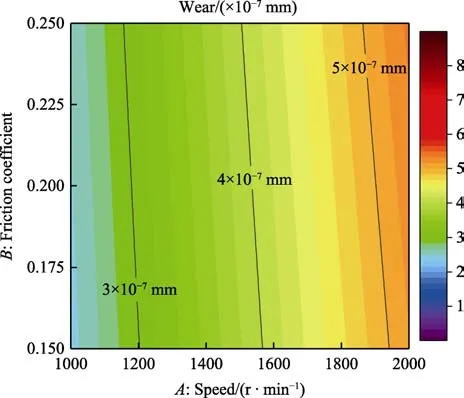
图14 换挡力为700 N 时摩擦系数和转速对磨损量影响的等高线图Fig.14 Contour map of the influence of friction coefficients and speeds on wear when the shifting force is 700 N
4 结论
在AMT 的换挡过程中,同步器换挡滑块与接合套在摩擦时存在以粘着磨损为主的早期磨损。本文利用仿真试验代替传统试验,研究了换挡过程中接合套的转速、摩擦系数、换挡力三者对换挡滑块磨损量的影响规律。主要结论如下:
1)通过BOX 响应面分析方法对仿真试验结果进行分析,获得了换挡滑块磨损量的预测优化模型,可以有效预测换挡滑块在换挡过程中的磨损量。
2)接合套转速、摩擦系数、换挡力均为换挡滑块磨损量的主要影响因素,磨损量分别随3 个影响因素的增大而增大。摩擦系数为0.15~0.25 时,对换挡滑块磨损量的影响较小。而在本文研究的水平范围内,接合套转速和换挡力对换挡滑块磨损量的影响更为显著。
3)在相同的摩擦系数与换挡力作用下,随着转速的增加,磨损量在单位转速内的增量略有下降。此外,接合套转速与换挡力对换挡滑块磨损量影响的交互作用显著。
因此,在接合套转速与换挡力需要同时增大的情况下,如果可以控制其中一项的增量值,可以有效地减小换挡滑块与接合套在换挡过程中的磨损量。特别是在高转速的情况下,在换挡策略中优先控制换挡力的大小,对于磨损量的控制效果更为明显。
