聚焦本质 多元探索
——《圆的面积》教学设计(二)
2021-05-06王小波
文|王小波
【教学内容】
人教版六年级上册第67、68 页。
【教学过程】
一、课前探究,唤醒转化意识
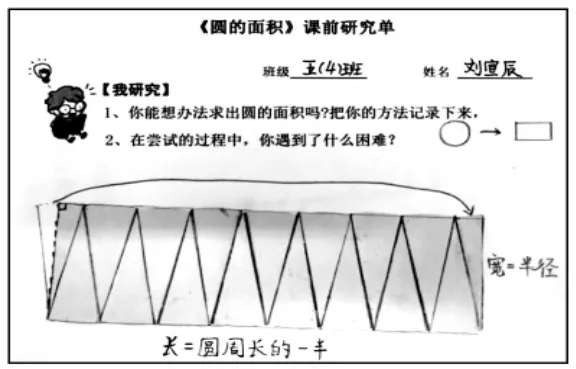
课前,教师布置前置性作业:

上课之前,教师收集学生的《研究单》,获知大多数学生都想到了要把圆的面积转化成已经学过的图形的面积。
【设计意图:求圆的面积对于学生来说是困难的,相较于以前学过的平面图形,它不容易转化,但那些平面图形面积推导时运用到的“转化”思想早已在学生的心中打上了深深的烙印。课前研究给学生足够的时间和空间,让他们能够像数学家一样地思考,亲历探究“圆的面积”的求解过程,形成丰富的个体经验,为课中的深度对话交流做好准备。】
二、课内研习,感悟转化思想
1.组内研习,初步感知“转化”思想。
师:关于“圆的面积”,大家已经做了课前研究,现在小组内把你想到的方法、遇到的困难以及如何解决进行分享。
(聚焦其中一个小组)
组长:我想到了转化成长方形,因为平行四边形、三角形等图形的面积都是转化成长方形的。
组员1:我也是转化的。刚开始我还想画上“格子”,用数格子的方法数出圆的面积,但我遇到了困难:我发现圆是曲线图形,外面的部分没法数。所以我就想,怎么把圆转化成规则图形呢?
组员2:我就是转化的,我把圆形纸片平均剪成了8 个小扇形,再把它们一正一反地拼在一起,拼成了一个平行四边形。
组员1:这个不是平行四边形。平行四边形的边是直的,你这个上下都是有圆弧的。
组员3:我也发现了这个问题,后来我发现把这些扇形再继续平均分,圆弧就越来越小。所以,我就把圆形当作一个近似的平行四边形来计算。

组长:我们分得份数越多,就会越接近一个平行四边形。那这个平行四边形的面积要怎么求呢?底和高分别是什么?
组员3:平行四边形的底就是圆周长的一半,这个我们可以从图上看出来,我作出它的高,发现平行四边形的高就是圆的半径。
组员1:把最左边的一个扇形从中间剪开拼到右边,就转化成了长方形,长方形的长和宽分别是圆周长的一半和半径,所以圆的面积是化简一下是πr2。
【设计意图:教师深入小组中仔细聆听小组内讨论的过程。尽管每个小组学生的情况不尽相同,讨论的方法和深度也不完全一致。但相似的是,经过了课前充分地探究,小组交流时,已经能够全身心投入其中,借助所有组员的力量,全方位地进行思想的碰撞:把自己的困惑提出来,小组内的成员说出自己的看法,尽可能尝试解决问题。尽管此时,也许有学生的理解还是“囫囵吞枣”,对知识点不够清晰明了,经其他组员的点拨,已经略有所悟,这些都为全班的交流打下了基础。】
2.全班交流,进一步深化“转化”思想。
师:刚才每个小组都进行了深入的交流,有的组甚至交流出了多种不同的转化方法,下面全班来理一理《研究单》中的问题。
生:我们组想到了转化的方法,把圆形纸片平均剪成若干个小扇形,穿插在一起,拼成了近似的平行四边形。平行四边形的底和高分别是和r,所以,圆的面积是πr2。我们的困惑是,这个面积到底是近似的还是准确的?
师:这个困惑解决了吗?
生:刚开始,我觉得是近似的,但我们组讨论后发现,如果平均分的扇形越来越小,它是接近三角形的,所以如果分得足够多,拼成的应该就是平行四边形。
师:其他组有什么想法吗?
生:我觉得你说得还不够准确,如果平均分的份数无限多,就会拼成一个长方形。
师:我们发现,分的份数越多,小圆弧将会越短,但是像这样继续分下去,拼成的图形会变成长方形吗?
师:我这有张圆形纸片,谁来平均分成256 份试试看?
(学生纷纷表示,分成256 份太麻烦了,实际操作会有误差)
师:我们可以请电脑来帮忙,你们任意说平均分的份数,我们用“几何画板”来进行操作。

注:2n 表示平均分的份数。
师:你发现了什么?
生:现在是200 份,拼成的图形已经非常接近长方形了,如果真的是无数份的话,拼成的就是长方形了。
生:原来我拼成的是平行四边形,我想到平行四边形可以剪下一个三角形平移拼成长方形,也可以把圆转化成长方形的,现在我知道了,其实不用进一步转化,份数足够多时,拼成的就是长方形。
师:看来大家已经体会到如何把圆转化成长方形了,那么圆面积的计算公式怎样推导呢?
生:长方形的长相当于圆周长的一半,宽相当于圆的半径,因此圆的面积公式是πr2。
师:那么圆是不是只能转化成长方形呢?你们小组是怎样探究的?
生1:我把圆形纸片平均分成16 份,拼成了一个梯形,梯形的上底和下底的和是8 个小圆弧,也就是圆周长的一半,梯形的高是2个圆半径的长度,因此,圆面积就是C÷2×2r÷2,化简后也是πr2。

生2:我是把圆平均分成了9份,拼成一个三角形,三角形的底是3 个圆弧的长,也就是圆周长的,高是3 个圆半径的长度,所以圆面积就是
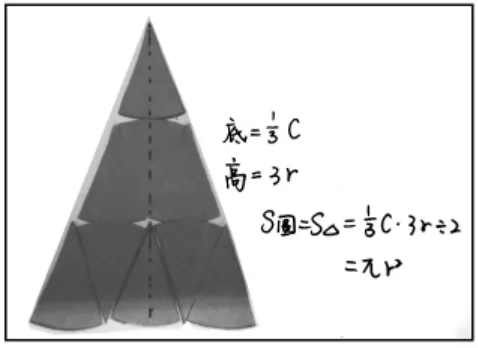
生3:我还有不同的方法。我把圆片平均分成8 份,1 份是一个近似的三角形,底是圆周长的,高是圆半径的长度。一个三角形的面积是,8 个三角形就是
师:同学们真厉害,利用梯形、三角形的面积也推导出了圆的面积,圆等分之后还能拼成其他图形,比如说组合图形。
生:我们组刚开始就是拼成组合图形,但是求面积太麻烦了。
师:那么众多的转化方法中,你会优先选择哪种呢?
生:当然是长方形,它是所有图形的基础,也是最容易推导的。
【设计意图:把圆的面积转化成长方形是最常见、最理所当然的。然而这并不意味着一想到转化,学生就会想到转化成长方形,也不见得就能转化成功。在课堂上,学生抛出“转化成的面积是准确的还是近似的?”这个问题,在讨论中借助动画的演示,学生体会到“极限”思想。在汇报时,学生的思维发散到转化成不同的平面图形来求圆的面积,不再局限于教材的表面处,而是基于学生的元认知,创新于教材的潜隐处。自主的探究加上课堂中充分地表达,让每一位学生都卷入其中,学有所悟,深刻领悟了转化思想:把复杂的内容简单化,陌生的内容熟悉化。用好转化思想,让数学学习更加智慧、更加灵动。】
三、创新练习,运用转化方法
师:知道了圆面积的计算公式,我们试着来解决一些问题。

【设计意图:练习的设计都是求圆的面积,但难度层层递进,可以满足不同水平学生的需求。其中第2 题,更是要求学生能够判断出大圆和小圆面积之间的关系,从而解决生活中的实际问题,对学生知识的掌握以及能力的提升都大有帮助。】
四、全课小结
(略)
