一类三平移3-RRC 并联机构的运动学
2021-04-30罗建国邱杰清赵韵秋
罗建国,邱杰清,赵韵秋
(1.华北科技学院机电工程学院,北京101601;2.华北科技学院研究生院,北京101601)
1 引言
并联机构具有刚度较大、结构稳定、误差小、精度高、易于实现高速运动、结构简单等优点,使其在某些领域得到广泛的应用[1]。三平移并联机构是仅有一个位姿的特殊并联机构,广泛应用于精密加工、医学、微电子、精密测量等精密工程等领域。许多学者对三平移并联机构进行过研究,并提出了很多不同类型的三平移并联机构[2-5]。3-RRC 并联机构是一种结构简单的并联机构,在一定结构下可实现三维平移。文献[6]对一种各支链3 运动副轴线平行且对称的3-RRC 进行了速度和加速度分析,文献[7-9]分别对一种各支链3 运动副轴线平行且3 支链相互位置一定的3-RRC 进行了位置分析、特殊位形分析、工作空间分析。
对一类各支链3 运动副轴线平行的3-RRC 并联机构进行了自由度分析、正逆解求解、工作空间求解、奇异位形分析,并给出了简洁又快速的计算分析方法。
2 结构及坐标系建立
3-RRC 并联机器人,如图1 所示。它由三条结构相同的分支及动(上)平台和静(下)平台组成,各支链3 运动副轴线平行,并且各支链的第一个转动副和圆柱副分别固定在静平台和动平台上。在静平台和动平台内心处固联固定坐标系O-XYZ、动坐标系P-xyz,如图1 所示。使Y轴与转动副A1的轴线垂直,y轴与圆柱副C1的轴线垂直,Z轴与z轴垂直于静平台竖直向上,X轴与x轴由右手迪卡尔坐标系确定方向。设θi为AiBi绕转动副Ai的轴线逆时针旋转至与OXY平面平行的转角,φi为BiCi绕转动副Bi的轴线逆时针旋转至与OXY平面平行转角,OA2、OA3与OA1的夹角分别为δ2、δ3,转动副Ai和Bi轴线之间的距离为ai,转动副Bi和Ci轴线之间的距离为bi,动平台内接圆半径为r,静平台内接圆半径为R,其中θi、φi由机构的位形决定,ai、bi、r、R、δ2、δ3由机构的结构确定,(i=1、2、3)下同。
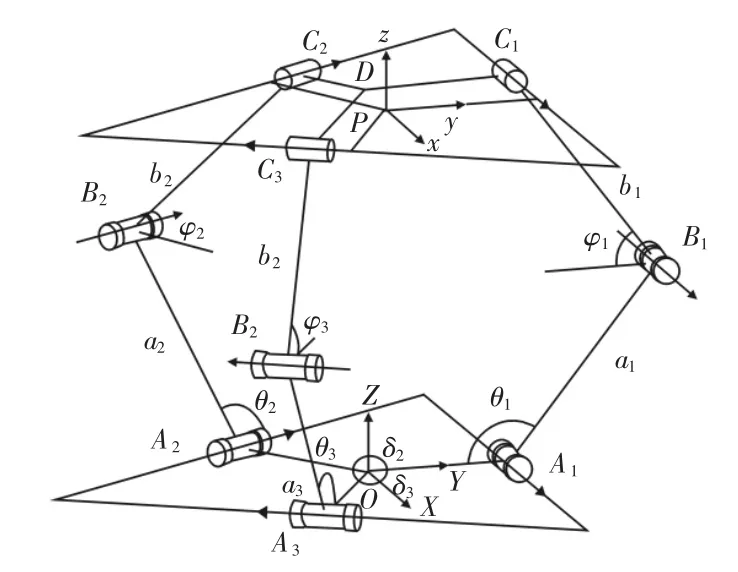
图1 三平移3-RRC 并联机构Fig.1 3-DOF Translational 3-RRC Parallel Mechanisms
3 自由度分析
基于螺旋理论(反螺旋)的自由度分析原理和修正的Kutzbach-Grübler 公式求解机构的自由度[10],该方法不仅可以计算机构的自由度数目还可以通过动平台约束螺旋系的反螺旋得到动平台的自由度性质。这里讨论的3-RRC 并联机构在任一位形下,圆柱副C1、C2、C3的轴线都平行于静平台,即动平台与静平台平行,在此前提下分别分析各支链。在支链i的Ai上建立坐标系Ai-xiyizi,如图2 所示。
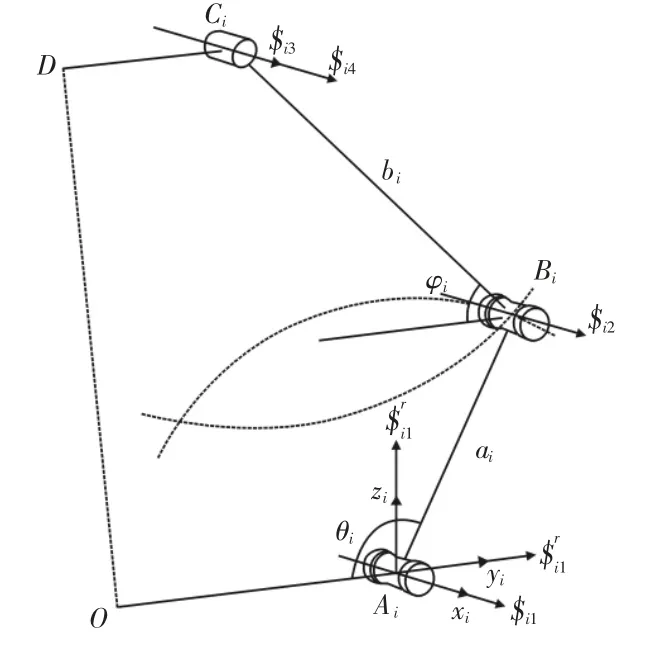
图2 支链结构Fig.2 One RRC Limb

支链i对动平台有2 个约束分别为垂直于动平台的约束力偶和平行于动平台的约束力偶。

表1 3-RRC 在非约束奇异位形下的自由度Tab.1 DOF of 3-RRC in Unconstrained Singular Configuration
综上可知,当3 个支链各自的3 个运动副轴线都不共面时,3 个支链对动平台有6 个力约束如表1 的第一种情况,其中3 个支链都施加了竖直向上的力约束,即公共约束λ=1,去除多余的公共约束后3 个支链对动平台只有3 个独立的约束,即冗余约束v=4-3=1。再对运动平台的约束螺旋系求反螺旋得到3 个独立的移动运动螺旋从而断定动平台具有3 平移运动。该机构的自由度可由修正的Kutzbach-Grübler 公式计算,考虑公共约束λ=1 和冗余约束v=1,有:
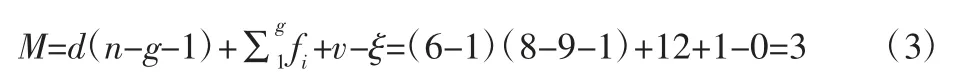
式中:M—机构的自由度;d—机构的“阶”由公共约束λ 确定,d=
6-λ;n—包括机架的构件数目;g—运动副的数目;fi—第i个运动副的自由度;v并联冗余约束;ξ—机构中存在的局部自由度。
假设支链i的3 个运动副轴线共面,同理可得到其约束反螺旋系有3 个螺旋为:

对比可知,3 个运动副轴线共面将对动平台多产生一个过AiBiCi的力约束,从而改变机构自由度和动平台自由度。分4 种情况分析,如表1 所示。
综上可知对于并联机构,当运动到特定位形时,有一条或几条支链上原来独立的运动螺旋变得线性相关则会在动平台上引入一个或几个新的约束螺旋,在新约束螺旋和旧约束螺旋组成的螺旋组中独立的新约束螺旋数和非独立的新约束螺旋数分别与动平台自由度减少数和机构自由度增加数相等。对于这里的3-RRC 并联机构,当且仅当至少有1 条支链的3 个运动副轴线共面时,有支链的运动螺旋线性相关必引入独立的新约束使得动平台自由度减少,机构处于运动奇异。
4 位置求解
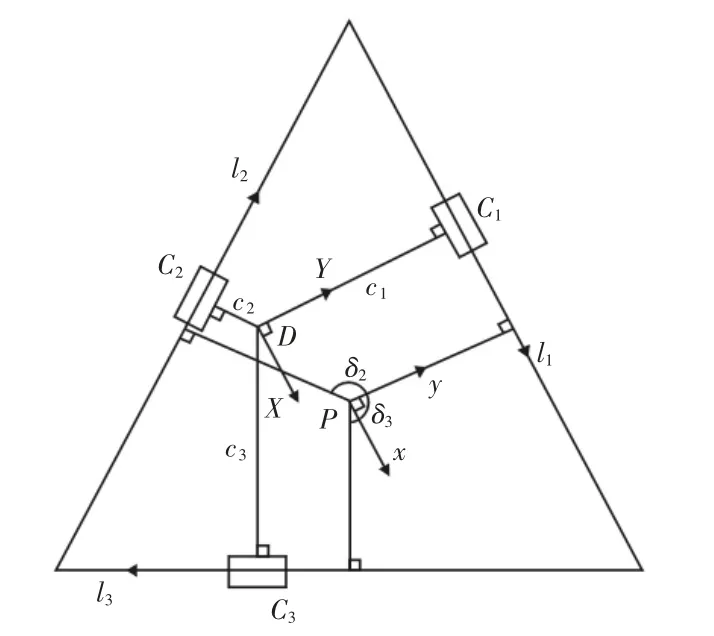
图3 动平台俯视图Fig.3 Top View of Mobile Platform
设动平台上点P在固定坐标系的位置为(XP,YP,ZP)T,并用Z-Y-X型欧拉角(α,β,γ)T表示动平台相对于静平台的姿态。由于机构处于任一位形下都有圆柱副C1、C2、C3的轴线分别平行于转动副A1、A2、A3的轴线,从而恒有α=0、β=0、γ=0。动平台俯视图,如图3 所示。DXY为静平台OXY在动平台上的投影,直线l1、l2、l3分别与圆柱副C1、C2、C3的轴线重合,c1、c2、c3分别为D点至C1、C2、C3的位移。在坐标系Oxy中,l1、l2、l3的直线方程及C1、C2、C3的坐标不难得到,再由点到直线的距离公式可求得c1、c2、c3如下:

4.1 位置逆解
位置逆解是当结构参数和动平台的位姿(XP,YP,ZP,α,β,γ)T给定时,求各支链作为输入的转动副的转角或移动副的位移。根据主动副确定准则,以每个支链的第一个转动副作为输入,即(θ1,θ2,θ3)T。由上面的分析可知这里的3-RRC机构仅有一个姿态,即(α,β,γ)T=(0,0,0)T,所以对于给定的位姿(XP,YP,ZP,α,β,γ)T≠(XP,YP,ZP,0,0,0)T时无解。下面对(XP,YP,ZP,α,β,γ)T=(XP,YP,ZP,0,0,0)T的情景进行求位置逆解。
取支链i求解,当XP、YP、ZP给定时可由式(5)可求出ci。在图2 中Ai-xiyizi坐标系下Ai、Ci坐标分别为Ai(0,0,0)、Ci(0,ci-R,ZP),则Bi为以Ai为圆心ai为半径的圆Ai与以Ci为圆心bi为半径的圆Ci的交点,Bi存在即逆解存在,其必要条件为:

二元二次方程组最多可有2 组解,如式(7)所示。每组解可确定唯一θi,可由下式解得:

综上可知对于这里的3-RRC并联机构当给定位姿(XP,YP,ZP,α,β,γ)T时,每条支链最多可有2 组解,3 条支链最多8 组解,即8 种位形。
4.2 位置正解
位置正解是已知结构参数和机构输入(θ1,θ2,θ3)T时,求动平台的位姿(XP,YP,ZP,α,β,γ)T。由于讨论的3-RRC并联机构仅有一个姿态,即(α,β,γ)T=(0,0,0)T,所以对于任意输入(θ1,θ2,θ3)T,动平台的位姿(XP,YP,ZP,α,β,γ)T=(XP,YP,ZP,0,0,0)T。
当给定(θ1,θ2,θ3)T时,在Ai-xiyizi坐标系下可得Bi(0,-ai Cθi,aiSθi)、Ci(0,ci-R,ZP),Bi、Ci两点间距离即为bi,可列出如下关系式:

三元二次方程组,最多可有8 组解,如式(10)所示。并且从式(10)可以看出正解为3 个圆柱面的交点,其轴线与半径分别如下:
(1)轴线方程:Z=a1Sθ1,-Y-r+R-a1Cθ1=0;半径为b1。
(2)轴线方程:Z=a2Sθ2,XSδ2-YCδ2-r+R-a2Cθ2=0;半径为b2。
(3)轴线方程:Z=a3Sθ3,XSδ3+YCδ3+r-R+a3Cθ3=0;半径为b3。
可以用CAD 软件绘制出对应的3 个圆柱体并求交得到相交体,顶点坐标即为正解。
5 工作空间求解
综合位置逆解中对3 条支链的分析,可知对于给定的动平台位置(XP,YP,ZP)T有位置逆解的充分必要条件为:当i=1、2、3时,XP、YP、ZP都满足式(6)。
所有有逆解的(XP,YP,ZP)T构成了这里3-RRC 并联机构的可达工作空间,其方程如下:
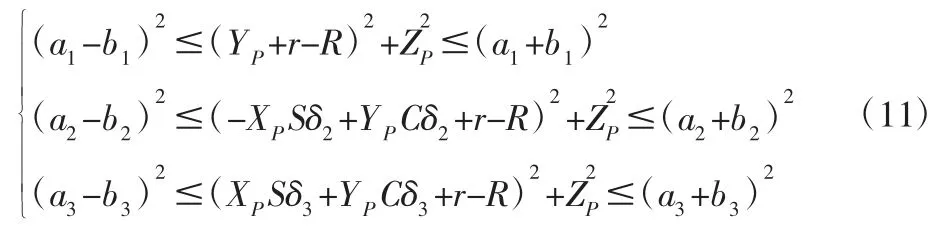
当(XP,YP,ZP)T位于可达工作空间表面时,式(11)至少有1个等号成立,即至少有1 条支链的3 个运动副轴线共面,机构刚好处于运动奇异。当至少有1 条支链的3 个运动副轴线共面时,式(11)至少有1 个等号成立,(XP,YP,ZP)T刚好位于可达工作空间外表面。所以处于运动奇异的所有位形与(XP,YP,ZP)T位于可达工作空间表面的所有位形一致。
式(12)的解为3 个空心圆柱的交。利用CAD 软件绘制对应的3 个空心圆柱并求交得到工作空间。
5.1 实例验证
给出结构参数a1=a2=a3=b1=b2=b3=200mm、r=25mm、R=50mm、δ2=δ3=120°。
将结构参数代入(11)得:
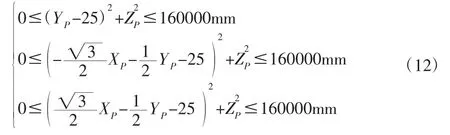
使用Autodesk 公司的AutoCAD 软件绘制了如图4(a)的3个圆柱体,并求交得如图4(b)的对称实体,即可达工作空间。利用AutoCAD 的查询功能可得到工作空间实体对象的一些信息,其中体积为290429255.0425mm3,顶点坐标也可得到,如图4 所示。

图4 工作空间求解Fig.4 Workspace Solution
下面对所得工作空间中的点求逆解再求反解以验证结果的正确性。
取图4(b)中工作空间的4 个顶点为动平台P点位置求逆解。已知结构参数,并分别取(XP,YP,ZP)T=(0,0,399.218mm)T、(-86.6025mm,-50mm,392.9058mm)T、(0,100mm,392.9058mm)T、(86.6025mm,-50mm,392.9058mm)T可得逆解,如表2 所示。由于选取了极限位移点逆解仅有一组。
正解计算:
取逆解计算中得到的4 组(θ1,θ2,θ3)T作为正解的输入。已知结构参数,并分别取(θ1,θ2,θ3)T=(86.4167°,86.4167°,86.4167°)T、(79.1931°,100.1931°,79.1931°)T、(100.1931°,79.1931°,79.1931°)T、(79.1931°,79.1931°,100.1931°)T可得正解,如表2 所示。
可以看出正逆解的计算值非常吻合,并且求得的所有正解仍满足式(12),验证了所求工作空间的正确性。

表2 实例位置正逆解 长度单位:mmTab.2 Inverse and Forward Position Solution of the Instance
6 奇异位形分析
按形成原因分奇异可分成2 类[11]:运动奇异、约束奇异。
对于分析的3-RRC 并联机构的运动奇异已经在自由度分析中给出了产生的条件,即至少有1 条支链的3 个运动副轴线共面,并在工作空间分析中给出了处于运动奇异的所有位形。下面分析约束奇异。
锁住该3-RRC所有的主动件,则获得一类各支链3 运动副轴线平行的3-RC并联机构,如表3 所示。做出其动平台约束分布图并进行自由度分析。
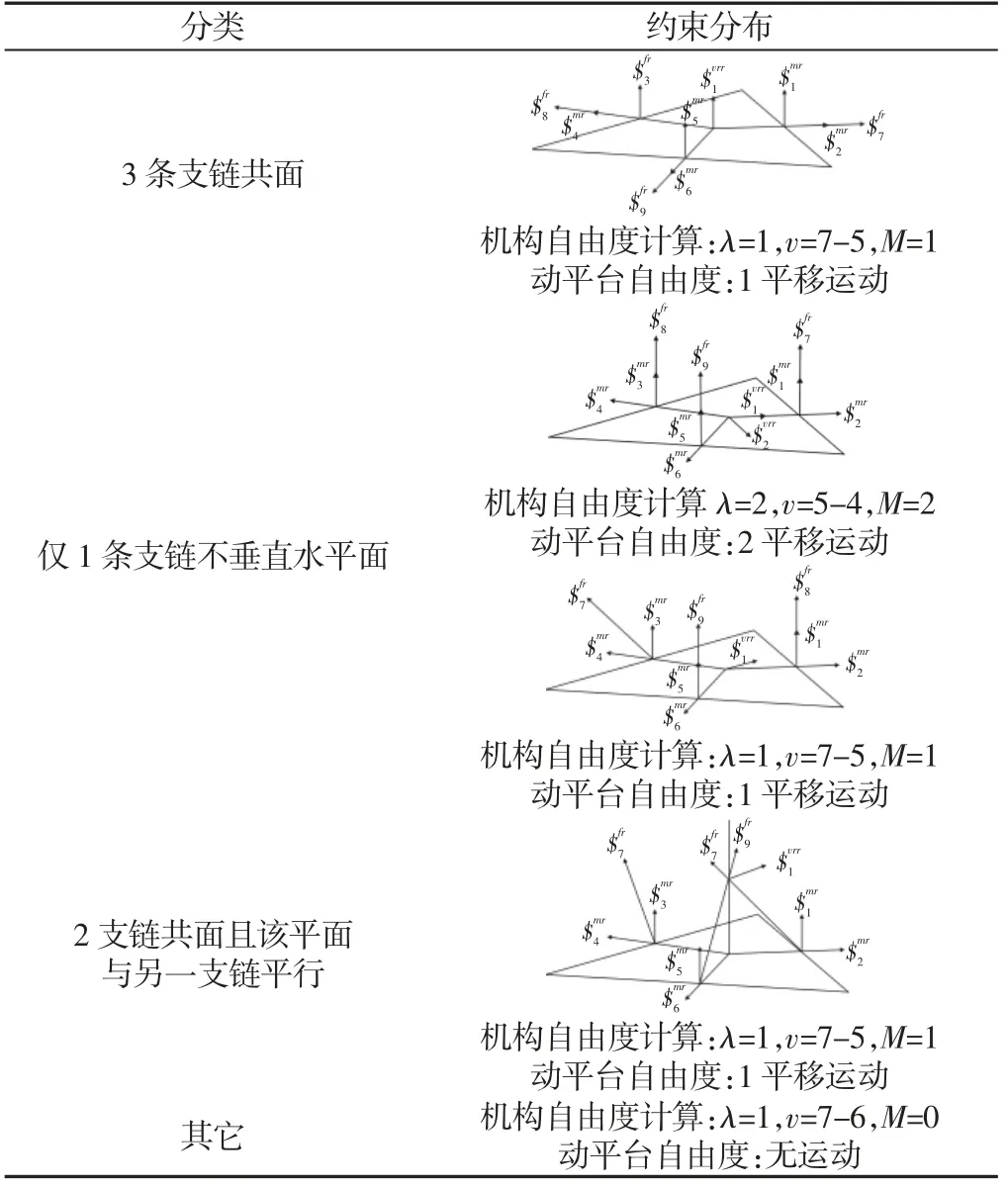
表3 3-RC 在不同位形下的自由度Tab.3 DOF of 3-RC in Different Configurations
当锁住所有的主动件所获得的3-RC并联机构具有表3 中的3 种特征,则此时3-RRC并联机构处于约束奇异。对比表1 和表3 可以发现存在3 种奇异分别为运动奇异、约束奇异、即为运动奇异又为约束奇异。结合表1 和表3 则得到了合理3-RRC并联机构机构任一位形下的自由度。
7 结论
(1)利用基于螺旋理论(反螺旋)的自由度分析原理结合动平台约束分布给出了机构在任一位形下的自由度,当3 个支链的3 个运动副轴线都不共面时,机构自由度为3、动平台有3 个平移运动。
(2)给出了正解、逆解,正解为3 个圆柱面的交点最多有8组解,逆解也可以通过求3 组两圆的交间接得到最多有8 组解。
(3)给出了工作空间的表达式,发现工作空间为3 个空心圆柱的交可直接用三维制图软件绘出工作空间,并发现动平台位置位于工作空间表面时的所有位形与所有运动奇异位形一致。
(4)在自由度分析的基础上给出了机构发生运动奇异与约束奇异的几何条件。
(5)给出的计算分析方法即简洁又快速,可编制软件将该机构的自由度、位置正逆解、工作空间、奇异位形计算分析过程程序化,减少大量的重复工作将使得该类机构的设计及优化变得非常简便。
