行星轮转轴等宽曲线泵设计与仿真实验分析

邱林宾，金 纯

（北京科技大学机械工程学院，北京100083）

1 引言

液压泵是液压系统的动力来源，为整个液压系统供给能源，液压泵在工程机械、海洋船舶、航空航天等行业应用广泛[1-4]。作为液压系统元件中的主要部件，目前国内常规应用领域的液压泵技术比较成熟。但是，在非常规领域，例如医疗器械中的低噪声微型泵、生物化工中检测分析微小泵的应用较少，大部分都依靠国外进口[5-7]。主要原因是国内微型泵的设计体积比较大，而且精度和使用寿命低，运行不稳定，难以满足液压系统的动力要求。

依据莱洛三角形的结构模型[8-10]，设计出了一种行星轮等宽曲线泵。以莱洛三角形截面为原型的转子在正方形界面旋转一周，反推出转子中心的运动轨迹，从而设计行星轮转轴驱动转子符合此运动轨迹，初步设计等宽曲线泵的整体结构，并进行了仿真和实验分析，结果证明了泵整体结构设计和功能的正确性。

2 等宽曲线泵的数学模型

2.1 莱洛三角形中心旋转轨迹计算[11-12]

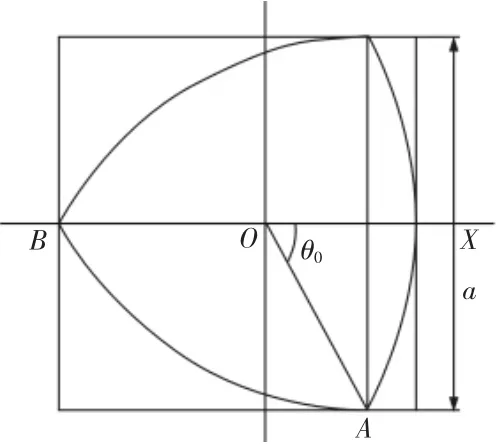
图1 莱洛三角形的初始位置Fig.1 Initial Position of the Leroy Triangle

以莱洛三角形中心的初始位置为原点O做坐标系xOy，如图1 所示。设莱洛三角形以ω1的角速度绕对称中心（原点O）进行顺时针旋转，起始θ0＝60°。

转动t时间后：θ＝θ0+ωt。莱洛三角形t时位置，如图2 所示。

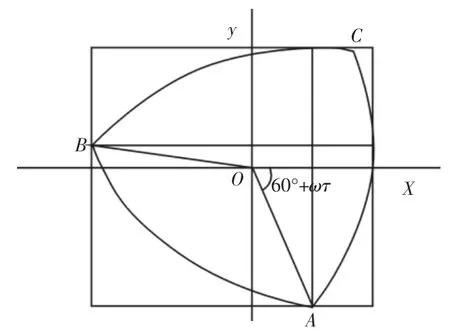
图2 莱洛三角形t 时位置Fig.2 The Position of the Leroy Triangle at t

正方形运动特点：

水平方向：

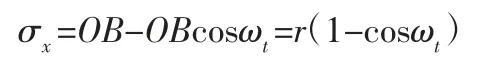
竖直方向：

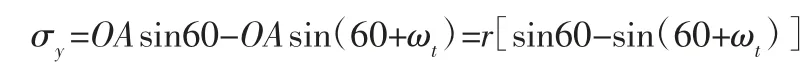
做逆向思维：将正方形看做是静止、莱洛三角形以ω 角速度匀速转动。则莱洛三角形中心轨迹为：

莱洛三角形旋转30°角度位置，如图3 所示。

图3 莱洛三角形旋转30°角度位置Fig.3 The Position of the Leroy Triangle Rotates 30°

对于a（x-d）2+b（x-d）（y-e）+c（f-e）2=f2的二次曲线的方程：

（1）当f≠0，b2-4ac＞0 时，双曲线。

（2）当f≠0，b2-4ac=0 时，两条平行直线。

（3）当f≠0，b2-4ac＜0，a＞0 时，椭圆。

（4）当f≠0，b2-4ac＜0，a＞0 时，虚椭圆（实平面上无图像）。

选取方程（1）其b2-4ac＜0，所以，当r≠0 时，它是一个椭圆；当r=0 时，则为一点。

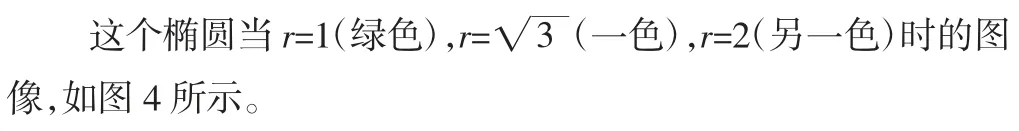
图4 方程曲线图Fig.4 The Chart of Equation

r=2 时，轨迹所在的四个椭圆方程的曲线，如图5 所示。

图5 四个椭圆方程曲线Fig.5 The Chart of Elliptic Equation

2.2 中心轨迹部分拟合设计

将转子中心轨迹包络部分取出，如图6 所示。

图6 转子中心轨迹Fig.6 Rotor Center Locus

对第一象限曲线进行研究。在其上等间距取出10 个点对其与原点的距离进行分析，如表1 所示。

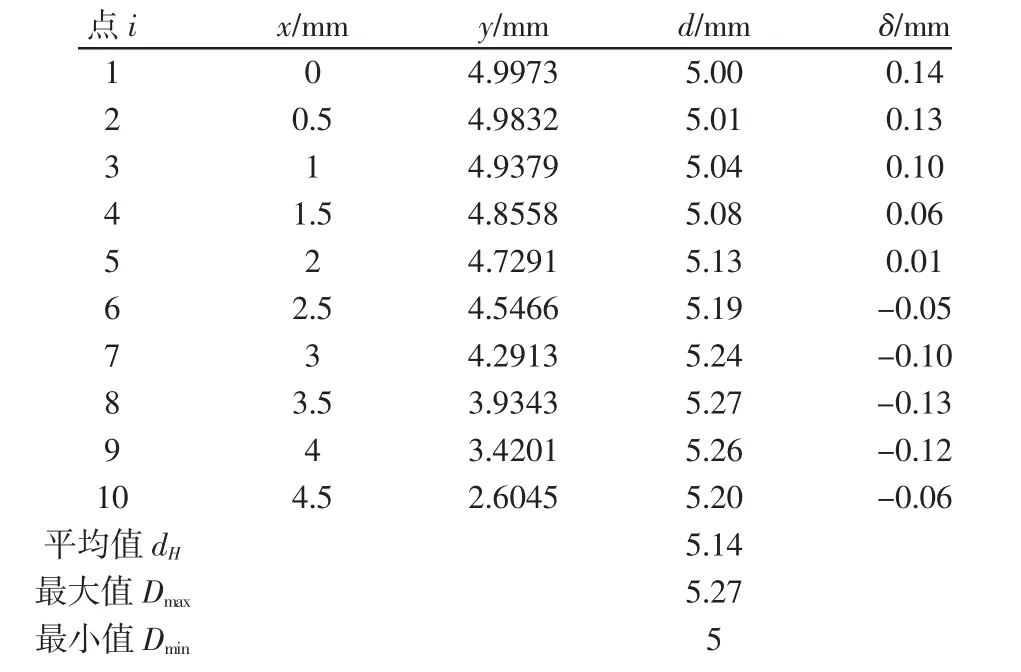
表1 间距与原点距离对照表Tab.1 Reference Table for Spacing and Origin Distance

容易看出：在曲线上所选取的10 个点到原点的距离全部在区间［5.00，5.27］之内，且在平均值（5.14±0.15）之内。当用所取各点到原点的平均距离dH=5.14 代替各点到原点的实际距离时，会得到以原点为中心，半径r=dH=5.14 的圆。用此圆代替原曲线会有一定的误差，但差值∂∈［-0.15，+0.15］在机械要求之内。可用半径r=dH的理想圆代替实际轨迹。这样为利用行星齿轮转轴的设计提供了方便。当转子中心轨迹用理想的圆代替时，可设计一对内啮合的行星齿轮副，使大小齿轮的分度圆直径比d1：d2=4：3。可以保证小齿轮在大齿轮内啮合转动过程中，其圆心轨迹为半径dH=1/8d2的圆且其公转角速度ω2等于三倍自转角速度ω1。

3 等宽曲线泵的几何模型设计

依据上述推导可得替代中心轨迹运动理想圆的实际轨迹。由于莱洛三角形转动时既有自转又在绕对应等宽正方形中心公转，故设计行星轮机构来实现这一过程。由于需要确保小齿轮在大齿轮内啮合转动过程中，其圆心运动轨迹为半径dH=1/8d2的圆且其公转角速度ω2等于三倍自转角速度ω1。这一运动关系可以采用分度圆直径比为4：3 的内啮合圆柱齿轮实现，传动简图，如图7 所示。

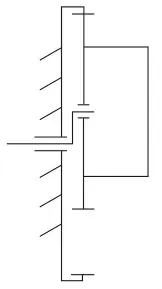
图7 传动简图Fig.7 Transmission Diagram

根据等宽曲线泵转子的转动特点及相应的近似替代设计泵实体，采用solidworks 软件建立等宽曲线泵的三维零件模型，并且装配成完整的三维实体模型。同时附加其材料属性并对模型产品运动的碰撞干涉分析，使建立模型与实际设计的参数一致，避免了生产过程中的不合理现象。

其内部结构和外部结构，如图8～图11 所示。

图8 转子内部结构图Fig.8 Internal Structure Drawing of Rotor

图9 内部传动结构图Fig.9 Internal Drive Structure Diagram

图10 内部结构图Fig.10 Internal Structure Diagram

图11 外形结构图Fig.11 External Structure Diagram

4 等宽曲线泵的运动学仿真与实验测试

4.1 动力学仿真验证

仿真验证方法以软件ADAMS 为仿真工具，设立等宽曲线泵模型，进行泵的运动分析。ADAMS 软件既具有很强的分析求解功能同时用户界面友好，使用起来直观方便[13-14]。行星轮转轴及转子在泵的工作过程中起关键作用，他们的正确与否关系设计能否实现。根据实际的运动学关系建立几何模型，分析等宽曲线泵运动学特点，如图12 所示。仿真关系图，如图13 所示。

图12 转子运动图Fig.12 Rotor Motion Diagram

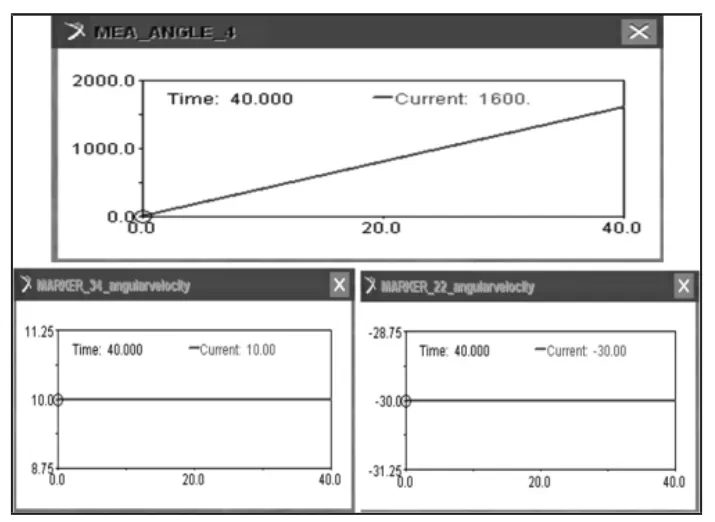
图13 仿真关系图Fig.13 Simulation Diagram

令行星轮转轴匀速转动，纵坐标为旋转角度，横坐标为时间，如图11 所示。曲线设定为一条直线。在此设定条件下，观测图12 得到行星齿轮的角速度ω=10°/s，与行星架的角速度ω=-30°/s成1：3 的关系。即转子中心自转、公转角速度的1：3 关系。

莱洛三角形旋转运动过程中与等宽正方形泵腔的交点A、B、C、D分离出a、b、c、d四个分泵腔。当莱洛三角形顺时针转动时，四个分泵腔各自完成3 个变化周期，如图14 所示。

图14 变化周期图Fig.14 Variation Period Diagram

应用ADAMS 将A、B、C三点在（1～4）状态之间运动过程中，转轴每转动一度所对应坐标采出，据此求出泵腔截面总面积，如图15 所示。

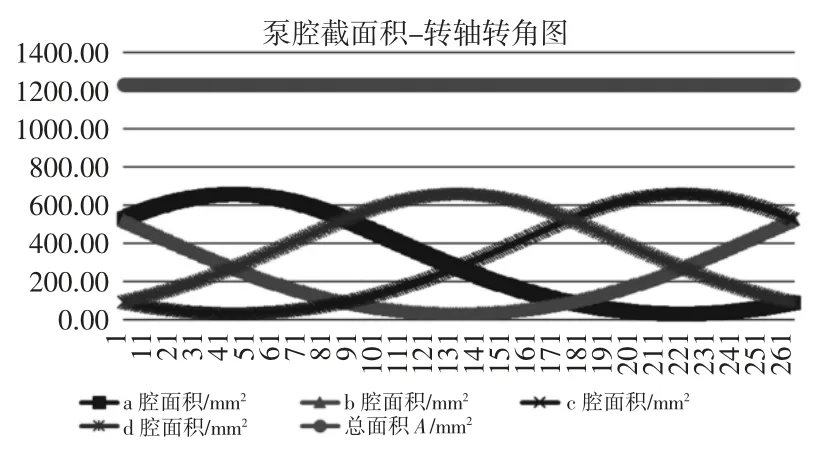
图15 泵腔截面积-转轴转角图Fig.15 Pump Cavity Sectional Area- Rotation Angle

从图中观察到：

单腔面积最大值amax为656.60mm2

单腔面积最小值amin为30.74mm2

泵腔总面积A为1232.04mm2

正方形面积-莱洛三角形面积：

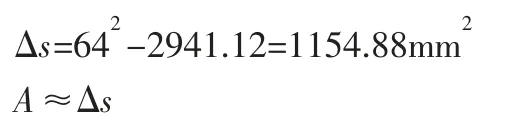
说明仿真过程正确，泵工作动力学特性成立。同时可以进行排量计算。

4.2 等宽曲线泵排量功率计算

4.2.1 泵排量计算泵腔截面总面积不变，这样减小了在输送流体过程中的脉冲。转子旋转一周泵腔完成三个吸进、排出周期，故每转总排量QT为：QT=3·4·（amax-amin）·h

式中：QT—每转总排量；

amax—单腔面积最大值，理论值为0.1594a2；

amin—单腔面积最小值，理论值为0.007a2；

h—等宽曲线泵腔长度；

则等宽曲线泵的几何总排量QT为：

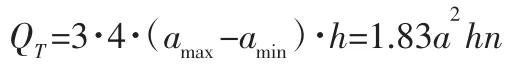
式中：a—泵腔变长，mm；

n—转子转速，转/s。

实际过程中存在泄露，实际排量减小，故引入容积效率ηv，实际排量为：

4.3 等宽曲线泵的实验测试

将设计加工好的等宽曲线泵安装在液压实验台上测试，实验测得在不同转速下流出流体体积为腔体容积的1.83 倍，验证了设计方法与仿真的正确性。不同转速下的流出体积与腔体容积比值，如图16 所示。

图16 不同转速下的流出体积与腔体容积比值Fig.16 Ratio of Outflow Volume to Pump Cavity Volume

5 结论

通过莱洛三角形在等宽正方形中旋转运动原理设计了行星轮等宽曲线泵，建立了严谨的数学模型和三维机械模型后进行动态模型分析，得到流出流体体积的理论值是泵腔容积的1.83 倍，远超过常规容积泵的26%，同时经过实验验证。因此能从理论上小型或者超小型化。为微型泵的设计提供了理论依据。