高精度无心车床主轴系统动力学建模研究
2021-04-30史丽晨王海涛
史丽晨,杨 帆,王海涛
(西安建筑科技大学机电工程学院,陕西 西安 710055)
1 引言
随着制造业的飞速发展,在轴承、航空航天、电子、机械等行业对圆钢、线材等银亮材的需求量巨大。但是一般圆钢在轧制、拉丝、挤压等工序过程中会存在表面裂纹、折叠等缺陷,有的棒材放置后会出现氧化皮,这些都极大地影响了钢材的表面质量[1],很难达到行业需求,因此需要对钢材的表面进行处理。
无心车床[2]作为一种去除管、棒、盘圆等长圆金属表面氧化层、裂纹,生产表面无缺陷的、具有较高尺寸精度、较低表面粗糙度且同轴度较高的光亮圆材的理想设备,同时其可替代传统酸洗工艺、普通车床与磨削加工[3]等落后生产工艺。通过车削将金属管、棒料表面的金属氧化皮去除,既避免了酸洗造成的水资源污染,也避免了磨削造成的粉尘污染,其加工工艺完全符合环保要求。广泛应用在轴承、航空航天、电子、机械等对圆钢、线材等需求巨大的行业。由于工作时主轴系统的不平稳,轴承与轴以及机架的结合面对无心车床动态特性的影响,造成刀具的颤振[4],会影响无心车床的加工精度。为了确保加工的动态精度,这就要求空心主轴系统有良好的动态特性[5]。
国外无心车床研究起步较早,工作效率高,加工精度高,而国内对无心车床的研究、整机加工精度和加工速度还不能进入高精度范畴,为数不多的研究集中在虚拟样机、控制系统研发中,缺乏对无心车床进行动力学建模研究与分析。针对现有研究的不足,建立无心车床主轴系统的动力学模型[6],通过对无心车床主轴系统动力学模型的simulink 仿真分析,得到主轴系统的仿真参数;最后通过实验参数进行对比,验证动力学模型的建立和分析结果的准确性。
2 无心车床主轴系统动力学建模
2.1 无心车床结构及工作原理
无心车床主要由空心主轴、前夹送装置、前导向机构、中后导机构、牵引小车组成,刀盘和刀具属于前导向机构。结构组成,如图1 所示。
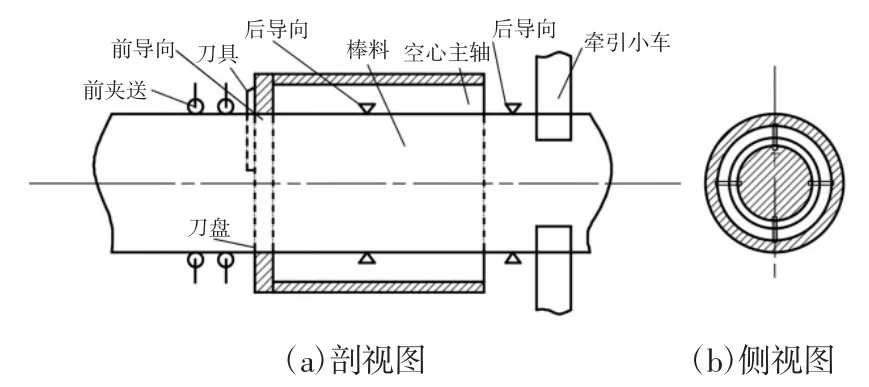
图1 无心车床结构简图Fig.1 Schematic Diagram of the Centerless Lathe Structure
无心车床车削棒料时,主轴前部的前夹送装置将棒料通过前导向送入空心主轴,空心主轴带动前端的刀盘(刀盘轴向均布四把刀具)高速旋转,从而实现棒料的被剥皮。棒料被剥皮加工时,由于不断进给,加工完成的部分由后导向夹持往后运送,当工件脱离前夹送装置后,后部的牵引小车夹住工件,确保工件做持续的轴向进给运动。
2.2 动力学建模
一般情况下,机床在加工过程中,刀具上的切削力可以分解成三个正交分量,即轴向分量(进给阻力)、径向分量(吃刀抗力)与切向分量(主切削力)。OXYZ坐标系,如图2 所示。

图2 无心车床主轴系统动力学模型Fig.2 Dynamic Model of the Centerless Lathe Spindle System
进行动力学分析[7],组成部分包括空心主轴、调刀套、刀盘、同步带轮和轴承。系统的激励力为主切削力Fs,进给阻力Ff,以及同步带轮作用在主轴上的压轴力Fr。系统的响应为刀具在轴向的位移z,以及径向的位移x,y。
由于无心车床在车削棒料时,切削过程极为复杂,影响因素甚多。因此,目前尚未形成统一的计算公式,这里按以下的经验公式[8]来计算各分力:
主切削力的计算公式为:
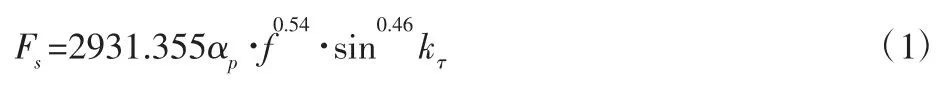
进给阻力计算公式为:

(2)假设电机启动后,同步带轮对主轴产生的压轴力Fr导致刀盘切削中心与棒料几何中心不对心,使主轴产生偏移。
基于以上假设,各刀具切削深度[9]会出现不同,导致主轴系统产生振动。
空心主轴的材料为45 钢,假设其为刚体。同步带轮对主轴存在压轴力使得空心主轴偏移,如图2 所示。假设轴承4 为固定铰支点,主轴刚体沿着压轴力的方向y 向产生侧向偏移。无心车床中的角接触球轴承1 的游隙为L4,则此空心主轴在轴承1 处产生L4的偏移量,那么空心主轴在刀盘处产生的偏移量LG可由线性关系求出。
在z方向,系统的激振力即是刀具的总进给阻力Ff。
在x方向,系统的激振力为刀具在x方向两个相对的刀具,由于切削深度不同导致吃刀抗力不同引起的力差产生的,记为ΔFp。吃刀抗力与切削深度差Δa的乘积即是x方向的激振力ΔFp。

式中:x—刀具在x方向的振动位移。
在y方向,同x方向,激振力由在x方向两个相对的刀具由于切削深度不同导致主切削力不同引起的力差产生的,记为ΔFs。

式中:y—刀具在y方向的振动位移。
根据达朗贝尔原理,可以推导出图3 所示系统的动力学微分方程为:
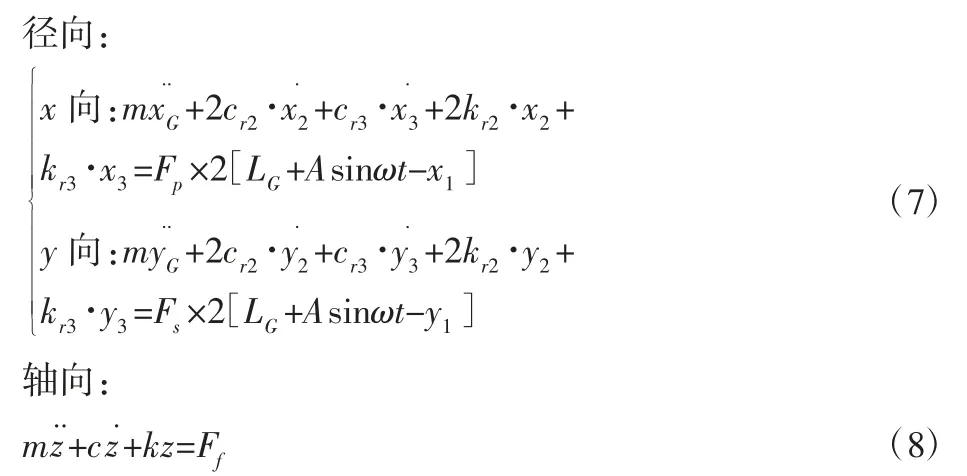
式中:m—主轴系统质量,40.356kg;
xG,yG—主轴的质量重心;
x2,x3—角接触球轴承3,4 处的游隙;
cr2,cr3—轴承(1 或2),轴承3 的径向合成阻尼;
kr2,kr3—轴承(1 或2),轴承3 的径向合成刚度;
c—轴承1,2,3 与轴套的轴向合成阻尼;
k—轴承1,2,3 与轴套的轴向合成刚度;
x1,y1,z—刀具在径向和轴向的振动量;
L1—刀具到轴承4 处的距离;
L2—轴承2 到轴承4 的距离;
L3—轴承3 到轴承4 的距离。
2.3 基本参数确定
基本参数确定如下,主轴系统尺寸参数,如表1 所示。主切削力,吃刀抗力,进给阻力,如表2 所示。轴承的轴向、径向阻尼,如表3 所示。轴套的各项参数,如表4 所示。

表1 模型图参数Tab.1 Model Diagram Parameters

表2 基本力的计算Tab.2 Calculation of Basic Force
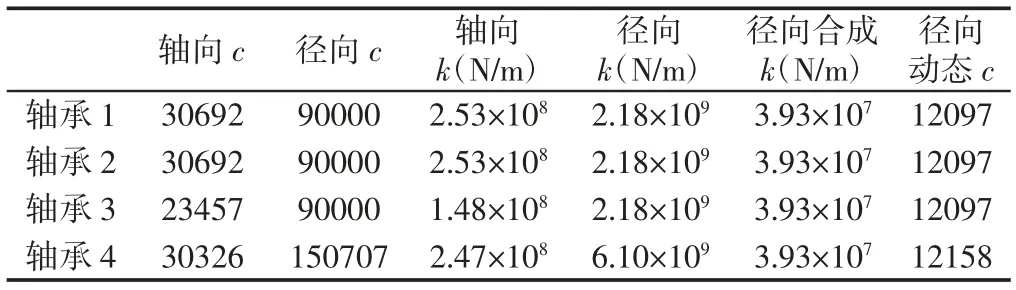
表3 轴承的刚度与阻尼Tab.3 Bearing Stiffness and Damping

表4 轴套的参数计算Tab.4 Parameter Calculation of the Bushing
3 主轴系统动力学仿真及结果分析
3.1 模型简化


3.2 动力学仿真
将所列的状态方程用MATLAB/simulink 模块进行仿真,如图3 所示。
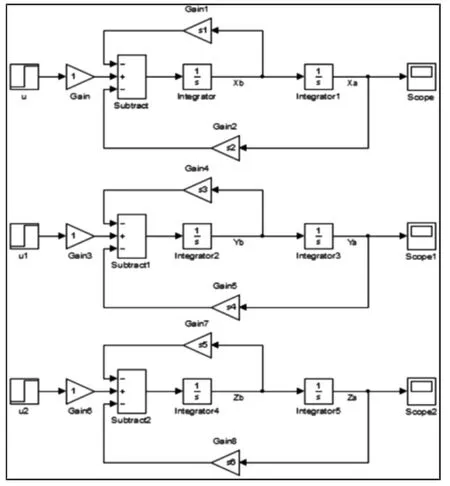
图3 无心车床主轴动力学的simulink 框图Fig.3 Simulink Block Diagram of the Spindleless Spindle Dynamics
3.3 仿真结果及分析
3.3.1x方向仿真图
当径向1(x方向)的轴承径向游隙[10]分别为0.03mm,0.04mm,0.05mm 时系统的振动,如图4~图6 所示。
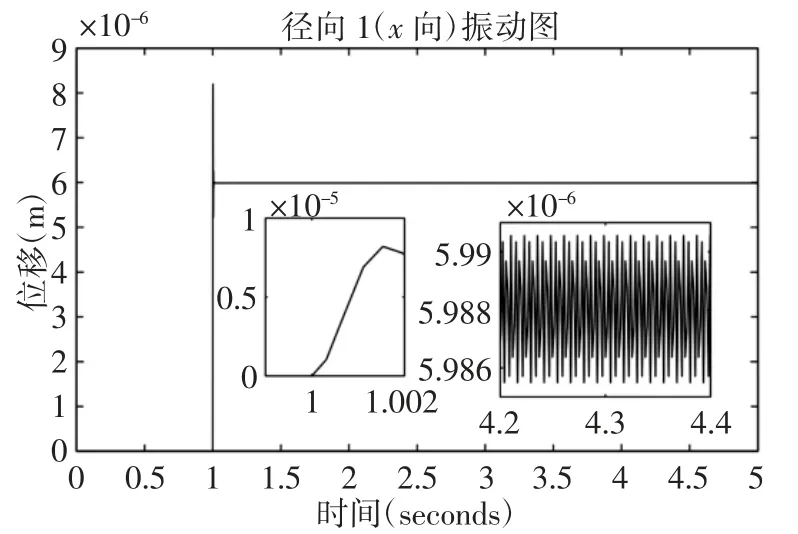
图4 Simulink 仿真信号图x 向(径向游隙为0.03mm)Fig.4 Simulink Simulation Signal Diagram x Direction(Radial Clearance is 0.03mm)
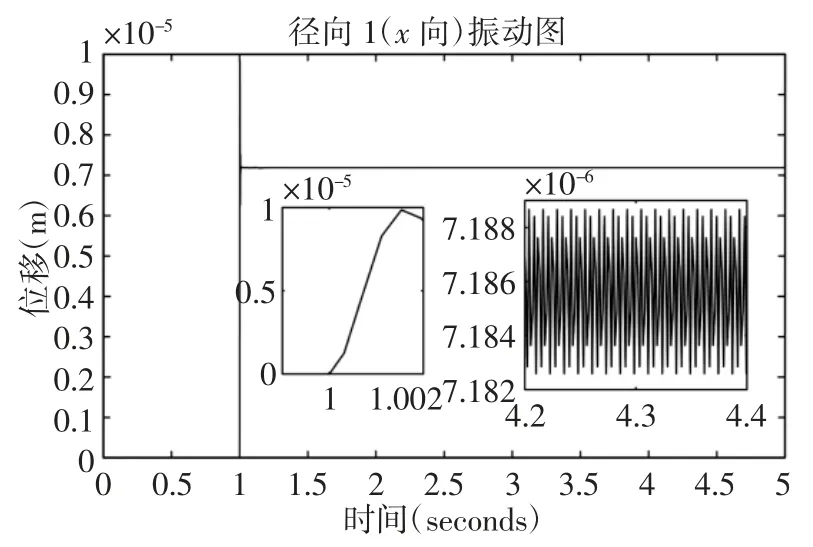
图5 Simulink 仿真信号图x 向(径向游隙为0.04mm)Fig.5 Simulink Simulation Signal Diagram x Direction(Radial Clearance is 0.04mm)
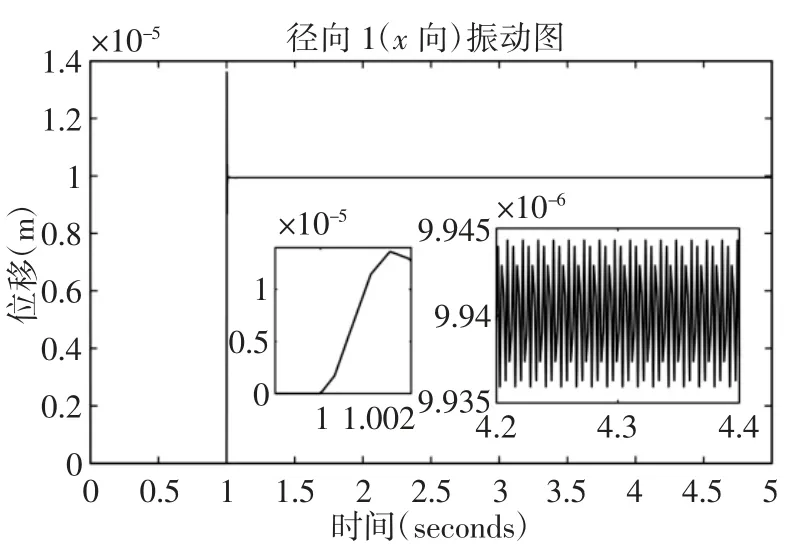
图6 Simulink 仿真信号图x向(径向游隙为0.05mm)Fig.6 Simulink Simulation Signal Diagram x Direction(Radial Clearance is 0.05mm)
通过simulink 仿真,得到主轴系统径向1(x方向)的振动信号。对x方向的稳定振动信号取平均值以及方差进行对比,如表5 所示。从仿真信号图和振动特性图中可以看出,在转速一定的情况下,无心车床对棒料进行切削,当振动稳定时,径向1(x向)在径向游隙为0.03mm 时的振动幅值为0.6×10-2mm,在径向游隙为0.04mm 时的振动幅值为0.719×10-2mm,在径向游隙为0.05mm 时的振动幅值为0.945×10-2mm,这说明随着径向游隙的增大,x方向的振动幅值逐步增大。振动位移方差不断增大,说明稳定时的微小波动越来越明显。

表5 X 向振动特性仿真参数比较Tab.5 Comparison of Simulation Parameters of X-Direction Vibration Characteristics
3.3.2y方向仿真图
当径向2(y方向)的轴承径向游隙分别为0.03mm,0.04mm,0.05mm 时系统的振动,如图7~图9 所示。通过simulink 仿真,得到主轴系统径向2(y向)的振动信号。对y方向的稳定振动信号取平均值以及方差进行对比,如表6 所示。在转速一定的情况下,无心车床对棒料进行切削,当振动稳定时,径向2(y向)在径向游隙为0.03mm 时的振动幅值为1.4975×10-2mm,径向游隙为0.04mm 时的振动幅值为1.973×10-2mm,径向游隙为0.05mm 时的振动幅值为2.484×10-2mm,可见随着径向游隙的增大,y方向的振动幅值逐步增大大。振动位移方差不断增大,说明稳定时的微小波动越来越明显。
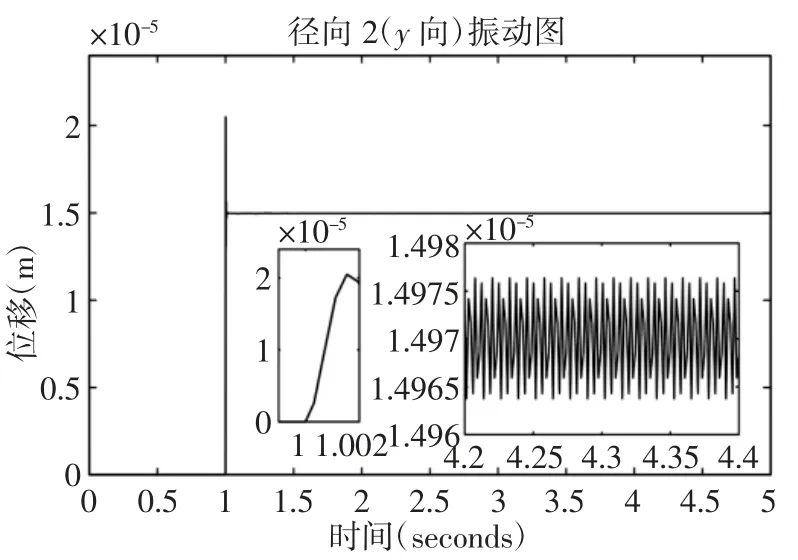
图7 Simulink 仿真信号图y 向(径向游隙为0.03mm)Fig.7 Simulink Simulation Signal Diagram y Direction(Radial Clearance is 0.03mm)
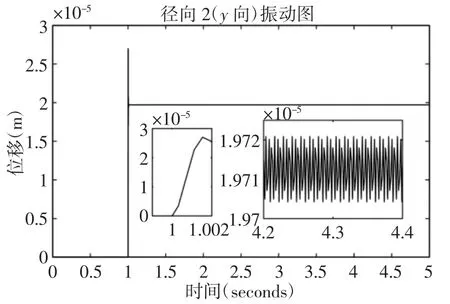
图8 Simulink 仿真信号图y 向(径向游隙为0.04mm)Fig.8 Simulink Simulation Signal Diagram y Direction(Radial Clearance is 0.04mm)
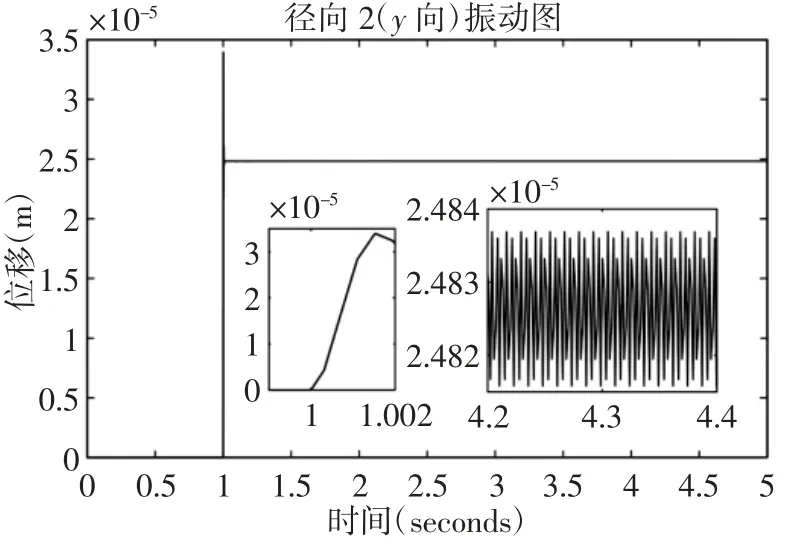
图9 Simulink 仿真信号图y 向(径向游隙为0.05mm)Fig.9 Simulink Simulation Signal Diagram y Direction(Radial Clearance is 0.05mm)
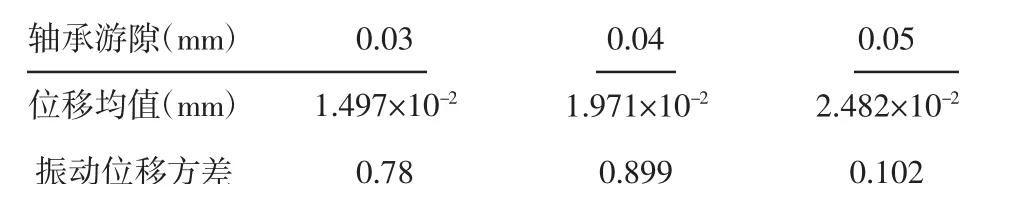
表6 Y 向振动特性仿真参数比较Tab.6 Comparison of Simulation Parameters of Y-Direction Vibration Characteristics
3.3.3z方向仿真图
当轴向(z方向)的轴套轴向磨损量分别为0mm,1mm,2mm时系统的振动,如图10~图12 所示。通过simulink 仿真,得到主轴系统轴向(z方向)的振动信号。对z方向的稳定振动信号取平均值以及方差进行对比,如表7 所示。从仿真信号图和振动特性图中可以看出,在转速一定的情况下,无心车床对棒料进行切削,当振动稳定时,轴向(z向)在轴承端面磨损为0mm 时的振动幅值为4.04×10-2mm,在轴承端面磨损为1mm 时的振动幅值为4.18×10-2mm,轴承端面磨损为2mm 时的振动幅值为4.33×10-2mm,说明随着轴承端面磨损的增大,z方向的振动幅值越来越大。对于轴向(z向),随着轴套磨损量的增加其振动幅值逐步增大,稳定时的微小波动越来越小。同时对比表5~表7 的对比可知,在相同条件下,主轴系统在三个方向的稳态振动的大小发现z向的振动量较大。因此,在对车床进行结构调整应优先考虑轴向方面。
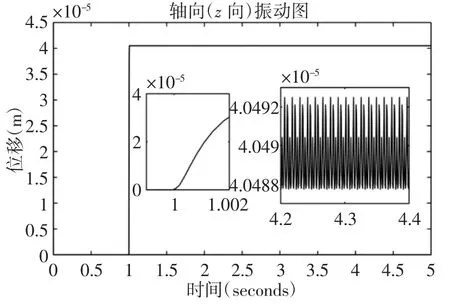
图10 Simulink 仿真信号图z 向(轴套磨损量为0mm)Fig.10 Simulink Simulation Signal Diagram z Direction(The Bushing Wear Amount is 0mm)

图11 Simulink 仿真信号图z 向(轴套磨损量为1mm)Fig.11 Simulink Simulation Signal Diagram z Direction(The Bushing Wear Amount is 1mm)
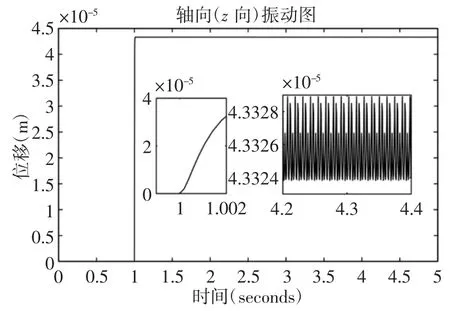
图12 Simulink 仿真信号图z 向(轴套磨损量为2mm)Fig.12 Simulink Simulation Signal Diagram z Direction(The Bushing Wear Amount is 2mm)
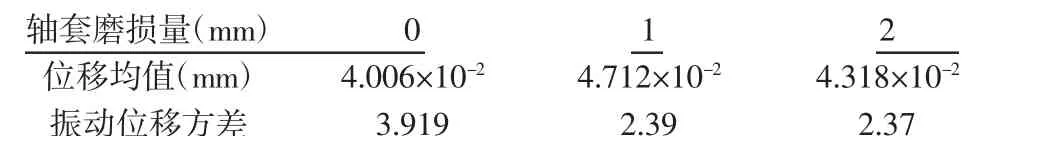
表7 Z 向振动特性仿真参数比较Tab.7 Comparison of Simulation Parameters ofZ-Direction Vibration Characteristics
4 实验验证
为了验证动力学建模以及仿真的结果,使用无心车床试验台进行实验验证,如图13 所示。对主轴在相同变化下的x、y、z方向的振动进行测试,在x、y、z三个方向布置传感器和连接测试系统等,用数据线连接到数据分析仪,数据分析仪再连接到计算机,从而完成整机实验系统的搭建。x,y,z向振动特性实验参数与仿真参数的对比,如表8~表10 所示。

图13 无心车床试验台Fig.13 Centerless Lathe Test Bench
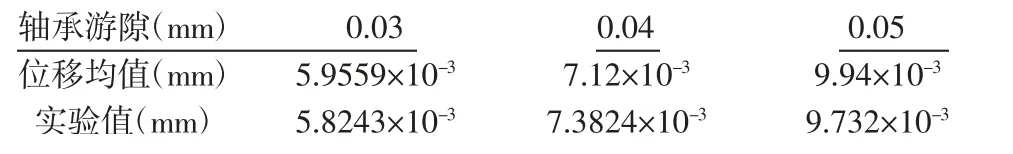
表8 X 向实验参数与仿真参数比较Tab.8 Comparison of X-Direction Experimental Parameters and Simulation Parameters

表9 Y 向实验参数与仿真参数比较Tab.9 Comparison of Y-Direction Experimental Parameters and Simulation Parameters

表10 Z 向实验参数与仿真参数比较Tab.10 Comparison of Z-Direction Experimental Parameters and Simulation Parameters
通过实验得出主轴在x,y,z三个方向的振动数据,与x,y,z方向的仿真数据进行对比,虽然动力学建模考虑了多方面的问题,但是与实际仍存在一定的差距,通过与实验数据的对比:径向1(x向)在轴承径向游隙为0.03mm 时,振动位移理论平均值为5.9559×10-3mm,实验平均值为5.8243×10-3mm;在轴承径向游隙为0.04mm时,振动位移理论平均值为7.12×10-3mm,实验平均值为7.3824×10-3mm;在轴承径向游隙为0.05mm 时,振动位移理论平均值为9.94×10-3mm,实验平均值为9.732×10-3mm。径向2(y向)在轴承径向游隙为0.03mm 时,振动位移理论平均值为1.497×10-2mm,实验平均值为1.37×10-2mm;在轴承径向游隙为0.04mm 时,振动位移理论平均值为1.971×10-2mm,实验平均值为1.765×10-2mm;在轴承径向游隙为0.05mm 时,振动位移理论平均值为2.482×10-2mm,实验平均值为2.412×10-2mm。轴向(z向)在轴承端面磨损为0mm 时,振动位移理论平均值为4.006×10-2mm,实验平均值为3.947×10-2mm;在轴承端面磨损为1mm 时,振动位移理论平均值为4.172×10-2mm,实验平均值为4.336×10-2mm;在轴承端面磨损为3mm 时,振动位移理论平均值为4.318×10-2mm,实验平均值为4.211×10-2mm。经过计算,径向1(x向),径向2(y向),轴向(z向)的振动实验值与理论值的误差均在5%以内,证明了模型建立的准确性。
5 结论
针对无心车床的主轴系统进行动力学建模与simulink 仿真,通过对主轴参数轴承游隙的改变来观察主轴径向1(x方向),径向2(y方向),轴向(z方向)振动的变化趋势以及改变轴套磨损量来观察主轴z方向的变化趋势并进行对比得到以下几点结论:(1)在给定条件下,主轴系统在三个方向上的振动幅值轴向最大。(2)主轴系统的振动大小与角接触球轴承的参数有关,角接触球轴承的径向游隙越大,主轴系统的振动幅值越大。(3)主轴系统的振动大小同样受轴套磨损的影响,轴套磨损越大,主轴振动幅值越大。(4)在给定的危险状态(棒料平面s弯在水平面)条件下,主轴系统z方向对主轴参数变化敏感,x方向,y方向对主轴参数变化不敏感。因此,在调整主轴参数时应注意其对z方向振动的影响。虽然动力学建模考虑了多方面的问题,但是与实际仍存在一定的差距,通过与实验数据的对比,证明了动力学模型建立的准确性。
