一般性拱轴线偏差对拱桥内力和稳定性的影响
2019-04-02
(重庆交通大学 重庆 400047)
拱作为一种以受压为主的结构,最为理想的拱轴线是与拱上各种荷载的压力线重合,在这种情况下,拱结构的各截面上只会存在轴向的压力且分布均匀。然而,对于实际工程而言,拱轴线偏离合理状态的情况几乎不可避免。
一、拱轴线偏差对拱桥内力的影响
(一)水平推力
(1.1)

(1.2)
因为矢高变化量f△一般很小,则水平推力的变化率可简化为:
(1.3)
又因为△f≪f,由上式(1.4)可知,拱圈内的水平推力对矢高变化的响应不大。
(二)轴线偏差引起的弯矩
假定原设计拱轴线为y0,成桥时实际拱轴线为y,则实际拱轴线较设计拱轴线的偏差为δ=y-y0;假定成桥时实际恒载压力线为y恒,则实际拱轴线较实际恒载压力线的偏差为η=y-y恒。由系统余能公式可得:
(1.4)
M=Нη=Н(y-y恒)
(1.5)
由上述可知,主拱圈任意截面的弯矩M与其对应的实际拱轴线较实际恒载压力线的偏差η有一定的函数关系。
二、拱轴线偏差对稳定性的影响
(一)面内轴线偏差
假设某一反对称的轴线偏差为:δ=αsin(2πx/l0),则拱轴线的压杆微分方程可以写成:
(1.6)
设:k2=Na/EIZ,则
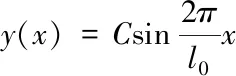
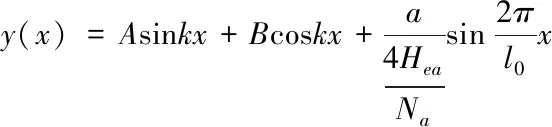
(1.7)
其中y(0)=y(l)=0,则式(1.9)改写为:
(1.8)
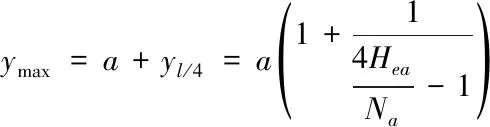
综上所述可得:
1.式中4Hea/Na=λa是稳定安全度,对于理想杆的临界平衡条件应为λa=1,当λa<1时,出现分支点失稳。由上式可知,当存在初始偏差a时,λa=1,则ymax→∞,表现为结构失稳。这说明拱结构失稳模态由第一类失稳(分支点失稳)变换为第二类失稳(极值点失稳)的根本原因是拱轴线平面内偏差的出现。
2.对于正对称偏差δ=asin(πx/l0)和反对称偏差δ=asin(2πx/l0)而言,若其偏差δ相同,则正对称偏差的a小于δ,而反对称偏差的a与δ相近,因此,正对称偏差的总附加绕度ymax比反对称偏差的要小,即稳定安全度更高,更不易失稳。
(二)面外轴线偏差
假设面外的拱轴线初始偏差:b(x)=b1sin(πxL0)
由此同理可建立平面外微分方程:
(1.9)
设:k2=Nb/EIy,则
上式一般解为:z(x)=Asinkx+Bcoskx,

(1.10)
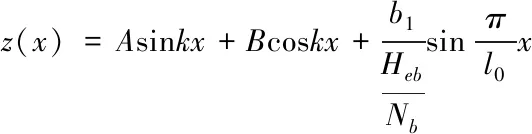
(1.11)
其中z(0)=z(l)=0,则式(1.14)改写为:
(1.12)
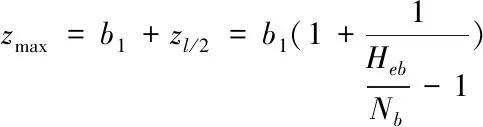
综上所述可得:
面外和面内轴线偏差的情况类似,同样会使得拱结构失稳模态由第一类失稳变换为第二类失稳,即失稳状况提前出现。但是与面内轴线偏差不同的是临界荷载取值不同,一般情况下比4Hea要大很多。
三、结论
1.拱桥施工中由于拱圈线形的变化,导致了恒载压力线也作出了相应的变化。因此,若仍以原设计拱轴线作为基础来控制拱圈轴线的偏差或对偏差进行评定,是不够准确的。
2.对于水平推力而言,其对一般性的拱轴线偏差的响应不明显,而弯矩对拱轴线偏差的响应情况就要看具体偏差的大小和类型了。正对称的轴线偏差,其轴力N、弯矩M的响应都很小。反对称的轴线偏差,由于反对称的轴线偏差水平夹角φ大,则其轴力不可忽略,为N=Н/cosφ,且η近似的等于a,则由偏差引起的弯矩为M=Нa。
3.面内和面外两种轴线偏差都会使得拱结构从第一类失稳转换为第二类失稳,而拱轴线初始的偏差又使得拱结构的失稳状态提前。对于一般性拱轴线偏差,即正对称和反对称偏差,当偏差相同时,正对称偏差引起的远小于,反对称偏差引起的更接近,因此正对称偏差比反对称偏差稳定安全度更高,更不易失稳。
