基于改进自适应趋近律的弹丸协调臂滑模控制
2021-04-27潘润超李志刚
潘润超,李志刚
(南京理工大学机械工程学院,江苏 南京 210094)
0 引言
滑模变结构控制本质是一种特殊的非线性控制,其非线性表现为控制的不连续性。滑模变结构控制在本质上的不连续开关特性会引起系统的抖振。在实际系统中,由于时间滞后开关、系统惯性等因素,使变结构控制在滑动模态下伴随着高频振动,抖振不仅影响了控制的精确性,增加了能量消耗,而且系统中高频未建模动态很容易被激发起来,破坏系统的性能。因此,关于变结构控制信号抖动消除的研究成了变结构控制研究的首要工作。
马天兵等[1]针对传统幂次趋近律中幂次系数过大会导致在滑模函数较小时,控制出现剧烈抖动,幂次系数过小会导致整个控制过程衰减速度过慢的问题,提出了一种自适应的幂次系数,根据系统状态变量来自适应调整幂次系数,最终通过壁板振动实验证明了算法的有效性。李永恒等[2]在结合幂次趋近律和变速趋近律基础上,提出了一种自适应趋近律,当系统状态变量距离滑模面较小时,变速项能根据状态变量自适应调节滑模面参数,直到系统状态轨迹运行到稳定点。廖瑛等[3]提出一种基于双幂次组合函数趋近律的新型滑模控制方案,在原有基础上,结合了一种非线性幂次组合函数,收敛速度比快速幂次或双幂次趋近律快,同时还保持了全局固定时间收敛特性,收敛时间上界与滑模初值无关。田野等[4]通过使用变指数幂次项,实现了系统在趋近过程中根据不同阶段进行自适应调节的功能,大幅提高了系统的收敛速度,并具有全局有限时间收敛特性。李慧洁等[5]针对滑模控制中传统趋近律存在抖振,收敛速度慢问题,提出了一种基于特定双幂次趋近律的滑模控制方法,能保证系统在存在有界集总干扰的情况下,滑模及其一阶导数在有限时间内收敛到稳态误差界内。Huang等[6]通过在趋近律里设计状态变量的积分项,来抑制抖振并提高响应速度,此外还提出了一种将恒定比例速率到达定律和指数到达定律相结合的IERRL,以进一步抑制颤动并消除直流母线电压的稳态跟踪误差。吕海龙[7]设计了一种基于幂次趋近律单向辅助面滑模控制方法,通过仿真验证了相比于常规滑模控制方法,具有更好的抗抖振能力。王杰等[8]采取分层滑模控制,并引入一种新的非线性趋近律并求取切换控制量,趋近速度相比于等速趋近律更快。Brahim 等[9]引入新的到达定律,通过提高系统轨迹的收敛速度,同时增加抖振衰减过程来解决抖振问题。邹权[10]利用自适应律调节切换律系数,使其在状态变量变化中围绕着某个值上下波动,保证状态变量有限时间收敛,有效减弱了抖振。
针对弹丸协调臂电液伺服系统在常规滑模控制下系统存在抖振和收敛速度慢问题,本文提出了一种基于改进自适应趋近律的弹丸协调臂滑模控制策略。在系统变量趋近切换面阶段,幂次项起主要作用,保证较快的趋近速度,在系统变量离切换面很近时,变速项起主要作用,且变速项增益系数能够根据状态变量大小自适应调节。以此期望能够保证系统变量有限时间收敛,且不会因变速项系数过大造成较大的抖振。
1 问题描述与动力学模型
1.1 弹丸协调臂机械部分动力学建模
弹丸协调器的工作原理为从接弹位将弹丸协调运动到与身管平行的输弹位。整个过程要求平稳,无冲击,到位误差控制在±3°以内,以保持较高的卡膛一致性,从而保证火炮弹药自动装填系统的可靠性,提高火炮射速。弹丸协调臂电液伺服系统模型如图1所示。

图1 弹丸协调臂电液伺服系统模型
图1所示模型中,点A和点O为系统的2个固定支撑点,点B为油缸支撑弹丸协调臂运动支点,点C和点D分别为协调臂质心和弹丸质心。具体参数定义如下:l为固定支点A与运动支点B之间的距离;l1为油缸支撑弹丸协调臂运动支点B到固定支撑点O的距离;l2和l3分别为协调臂架体质心和弹丸质心到固定支撑点O的距离;l4为固定支撑点A和固定支撑点O之间的距离;α为l4与竖直方向的夹角;θ为协调器协调角度,变化范围为0~90°;β为油缸推杆与协调臂架体的夹角;F为油缸推力;m1g为协调器架体所受重力;m2g为弹丸所受重力;p1为油缸无杆腔压力;p2为油缸有杆腔压力;ps和pr分别为供油压力和回油压力;μ为控制器输出到伺服阀的电压信号。
弹丸协调臂运动方程可表示为
Fl1sinβ-m1gl2sinθ-m2gl3sinθ=
(1)
1.2 弹丸协调臂液压部分动力学建模
油缸两腔的流量方程可表示为:
(2)
(3)
Q1和Q2分别为油缸无杆腔和有杆腔进油量或回油量;Cd为流量系数;阀芯位移xv=kvu,其中kv为伺服阀和放大器总增益,u为控制器输出控制电压;W为阀口面积梯度;ρ为液压油密度;且0≤pr≤p1≤ps,0≤pr≤p2≤p1;s(xv)为阀芯位移的函数,定义为
(4)
油缸两腔的连续性方程为:
(5)
(6)
1.3 弹丸协调臂状态方程推导
油缸两腔压力平衡方程为
A1p1-A2p2=F
(7)
结合式(1)~式(7)可得
(8)
K1、K2、K3和ΔF均为非线性未知可变函数。

(9)
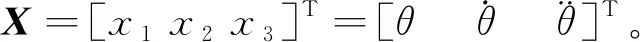
2 滑模控制器以及趋近律设计
2.1 系统滑模面设计
(10)
c1和c2均大于0,对于Laplace算子P,满足c1+c2P+P2为Hurwitz多项式。结合式(9)和式(10)可得
(11)
2.2 传统趋近律分析
传统指数趋近律为
(12)

文献[3]提出双幂次组合函数趋近律为
(13)
其中,a=1+γ,b=1-γ,δ=1,0<γ<1,k1和k2均大于0。
(14)
由于Fal函数的分段特性,双幂次组合函数趋近律在[0,δ]范围内比传统指数趋近律趋近速度更快,且全程控制连续。但是该趋近律第2项在s很小时,合适准确的k2取值难以通过调试获得,且在逼近切换面时切换增益偏大,引起系统抖振也较大。
2.3 改进自适应趋近律设计
结合上面所提到的趋近律,本文提出一种改进自适应趋近律为
(15)
k1>0,K(t)>0。改进自适应趋近律的第1项分段函数定义为
(16)
其中,a>0;ε为稳态误差界参数,ε>0。当运动点距离切换面较远时,采用幂次趋近律保证系统变量能以较大速度趋近于滑模面;当运动点距离切换面很近时,趋近速度很小,让改进自适应趋近律的第2项完全掌握趋近速度大小的调节,尽量加快趋近速度的同时减少抖振。自适应律为
(17)

2.4 稳定性证明
结合式(11),滑模面一阶导数采取改进自适应趋近律式(15)可转换为
u+ΔF=k1Kal-K(t)sgn(s)
(18)
由式(18)可得系统控制律为
(19)
定义Lyapunov函数为
(20)
γ为待定的常数,γ>0。对V求导可得
(21)
因为Kal函数和sgn(|s|-ε)大小由|s|大小决定,现分为以下2种情况分别讨论。
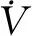
(22)
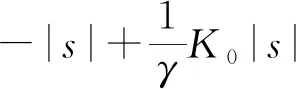
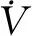
(23)
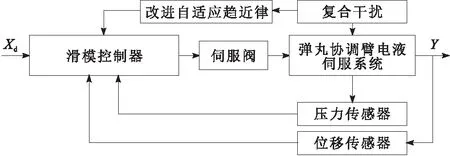
图2 弹丸协调臂电液伺服控制系统结构
3 仿真分析与验证
3.1 弹丸协调臂运动轨迹设计
根据实际系统在MATLAB/Simulink里建立弹丸协调臂仿真模型,并设计控制器。为了保证整个运动过程平稳,特别是在启停阶段没有过大的加速度突变过程,采用S型速度曲线规划算法,0~1 s内静止不动,1~2 s弹丸协调臂从0运动到60°,规划轨迹如图3所示。

图3 协调臂的运动轨迹规划
整个过程让加速度处于连续变化的规程,没有加速度突变的情况,有利于控制量不会产生突变,减少了协调臂在运动过程中因为控制量突变而引起的抖动,保证了较好的运动动态品质。
3.2 仿真结果与分析
最终获得的控制参数为:c1=20,c2=50,K0=1×10-5,k1=4×10-6,a=1.75,ε=2.6,μ=3×10-5、γ=1×10-6。在仿真模型中,给系统所加干扰为d(t)=120 sin(2πt)+50.6。系统控制输入电压,大小在-10~+10 V内,符合伺服阀输入要求。因为是单方向向上协调运动,即液压缸只伸出,所以控制电压为正。基于改进自适应趋近律控制输入电压如图4所示。
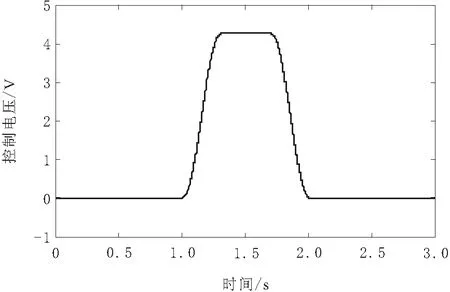
图4 系统控制输入电压
基于改进自适应趋近律弹丸协调臂运动位置跟踪误差如图5所示。
由图5可知,弹丸协调臂动态误差最大为0.11°,到位误差为0.01°,整个运动过程较平稳,无明显振动,满足实际工况需求。
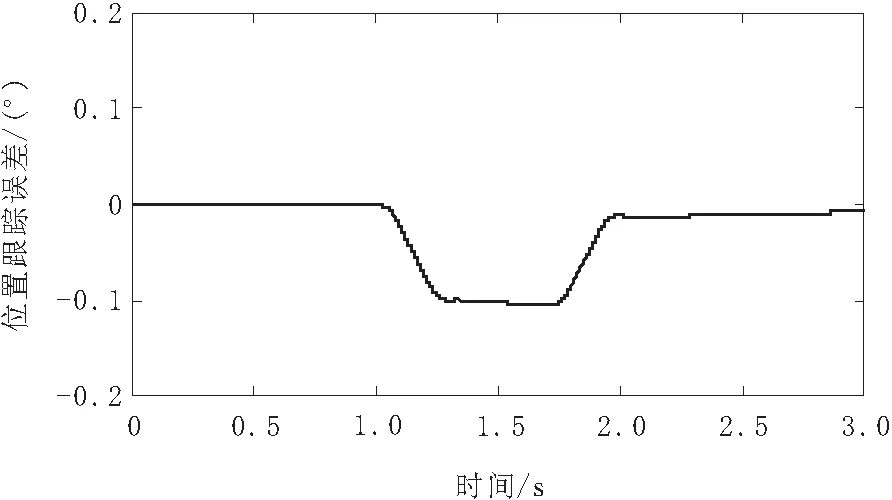
图5 位置跟踪误差
改进自适应趋近律增益自适应调整如图6所示。

图6 改进自适应趋近律增益K(t)变化曲线
由图6可知,变速项增益K(t)能在滑模变量s变化下自适应调节其本身大小,而不是以固定增益趋近切换面,这样可以使系统在保证趋近速度的同时又减少了抖振,实现动态调整。
3.3 不同趋近律下滑模变量s分析
为了证明改进自适应趋近律的有效性,在同等条件下分别测试在改进自适应趋近律、幂次趋近律和传统指数趋近律下弹丸协调臂运动过程中滑模变量s的变化情况。
3.3.1 改进自适应趋近律
调试参数为:k1=4×10-6,a=1.75,K0=1×10-5,μ=2×10-5,ε=1。基于改进自适应趋近律滑模变量s变化情况如图7所示。
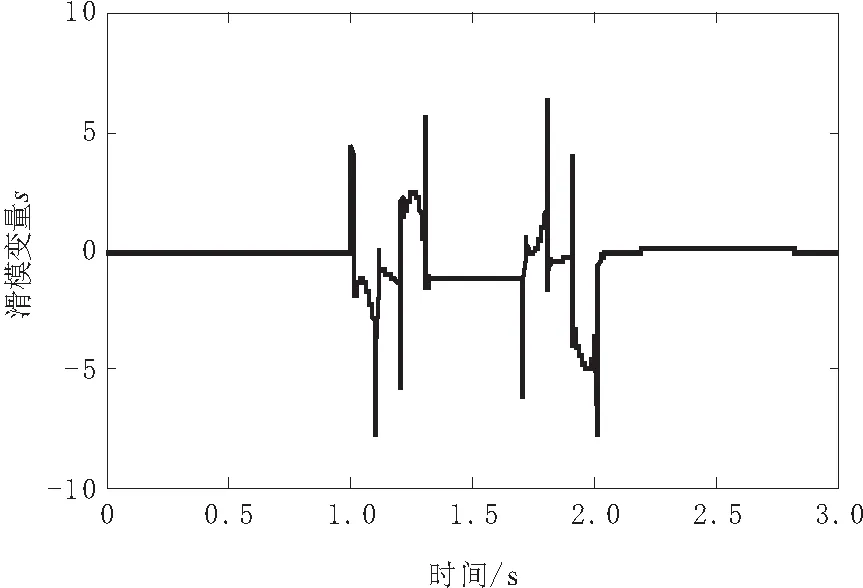
图7 基于改进自适应趋近律滑模变量s变化曲线
由图7可知,基于改进趋近律下的滑模变量s在受到系统参数不确定性和外部干扰时,s有一定幅度的波动,总体较为平稳,振幅不大,最大振幅为-7.6。状态变量能以较快的速度收敛到稳态误差宽度为2.6的范围内。
3.3.2 幂次趋近律
调试参数为:k1=4×10-6,k2=5×10-5,a=1.75,b=0.25,δ=1。基于幂次趋近律滑模变量s变化情况如图8所示。

图8 基于幂次趋近律滑模变量s变化曲线
由图8可知,基于幂次趋近律下的滑模变量s在受到系统参数不确定性和外部干扰时,波动较为明显,s最大振幅为-8.75,s收敛后的稳态误差范围为7.1以内。
3.3.3 传统指数趋近律
调试参数为:k1=4×10-6,k2=5×10-6,ε=1。基于指数趋近滑模变量s变化情况如图9所示。
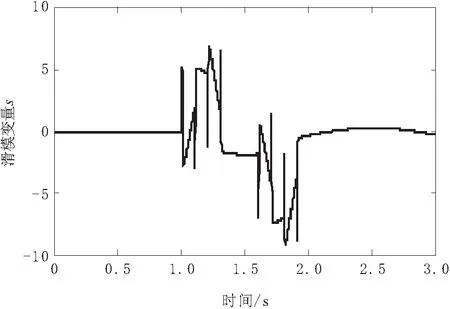
图9 基于指数趋近律滑模变量s变化曲线
由图9可知,基于改进趋近律下的滑模变量s在受到系统参数不确定性和外部干扰时,s波动较大,最大振幅为-8.74,s收敛后的稳态误差范围为9.0以内。
4 结束语
针对弹丸协调臂电液伺服系统在传统滑模控制下存在趋近速度慢,抖振严重等问题,提出了一种基于改进自适应趋近律的弹丸协调臂滑模控制策略,根据实际系统在MATLAB/Simulink里建立弹丸协调臂仿真模型,并设计控制器。
经过对模型进行仿真分析以及对不同趋近律下滑模变量s分析验证,得出以下结论:
a.所设计改进自适应趋近律能够根据系统状态变量s大小自适应调节其变速项增益大小,既保证了趋近速度又有效减弱了抖振。
b.将3种趋近律下的滑模变量s进行对比,所提出改进自适应趋近律下的滑模变量在受到系统参数不确定性和外界扰动的时候,波动振幅小,鲁棒性好,且能达到收敛稳态误差宽度为2.6的区域内,抖振较小。
c.在改进自适应趋近律控制下,弹丸协调臂能保持较高的动态精度和到位精度。
