超高速撞击下球形弹丸破碎特性仿真研究
2022-09-13盖芳芳生帝刘恂刘宝良
盖芳芳,生帝,刘恂,刘宝良
(1.广东石油化工学院 建筑工程学院,广东 茂名 525000;2.固安云谷科技有限公司,河北 廊坊 065000)
随着人类航天事业的发展,发射在地球近地轨道的航天器越来越多,造成在轨物体数量不断积累,空间环境也随之恶化[1,2]。空间碎片的高速碰撞会对正常运行的航天器造成损伤,甚至可能造成航天任务的失败。另外,空间碎片撞击后还可能形成新的碎片,对航天器造成二次损伤[3,4]。可见,对空间碎片撞击发生破碎后的破碎状态进行研究很有必要。由于试验技术的限制,通过试验能够获得的弹丸破碎状态数据有限,因此仿真手段成了目前研究弹丸破碎状态的主要手段。Piekutowski[5-7]对弹丸的破碎进行了大量的研究,为国内外研究者提供了真实可靠的试验数据。Kipp等[8]对撞击过程中弹丸的破碎状态进行了建模,给出了不同破碎模型下碎片尺寸及不同破碎模式转换的临界条件;Swift等[9]建立了在球形弹丸撞击速度为7 km/s时正撞击铝板形成碎片云的半理论半经验模型。国内也有很多学者对超高速撞击下的弹丸破碎状态进行了研究。如柳森等[10]对超高速拍摄设备进行了改进;张伟等[11,12]对柱形弹丸铝合金薄板形成的碎片云进行了建模,获得了弹丸破碎状态的质量及速度特性;迟润强[13]研究了当球形弹丸撞击薄板时弹丸和薄板的破碎状态,建立了碎片云模型,获得了弹丸破碎特性数据。本文使用我国航天常用铝合金材料Al2017、Al6061模拟弹丸及薄板,对球形弹丸撞击薄板后的破碎状态进行仿真研究,以期为我国航天器防护研究提供数据支持。
1 仿真模型建立
为了更准确地对弹丸的破碎状态进行描述,应用非线性动力学软件AUTODYN-3D,采用SPH方法三维建模,弹丸采用Al2017材料,薄板采用Al6061材料,SPH粒子直径0.1 mm,几何模型如图1所示。

图1 仿真的几何模型
2 弹丸破碎状态特性分析
2.1 弹丸破碎和完全破碎时的临界速度
确定不同弹丸直径下弹丸发生破碎的临界撞击速度vpc和弹丸发生完全破碎的临界速度vpcc。薄板厚度t取1.0 mm,弹丸直径dp取2.0~4.0 mm。图2给出了当弹丸直径为4.0 mm时不同撞击速度下弹丸的破碎状态。由图2可见,随着弹丸速度的增加,弹丸破碎得越厉害。

图2 不同撞击速度下弹丸的破碎情况
确定弹丸发生破碎时的临界速度。由图2不同撞击速度下弹丸破碎后的小碎片分布情况可见,当板厚为1.0 mm和弹丸直径为4.0 mm时,工况a弹丸基本无形变,且没有发生明显的破碎,而工况b则有较明显的形变,并且弹丸前端开始发生破碎。则弹丸破碎的临界速度在1.3~1.5 km/s间,取1.4 km/s为弹丸破碎的临界速度。根据上述计算方法,可以确定不同弹丸直径下弹丸破碎的临界速度,并绘制曲线,如图3所示。由图3可见,弹丸破碎的临界速度随着弹丸直径的增加而增加,且呈近似正比关系。
确定弹丸发生完全破碎时的临界速度。由图2可见,在弹丸撞击速度为6.5 km/s(图2h)和7.0 km/s(图2i)时,弹丸已经发生完全破碎;而在撞击速度为6.0 km/s时,碎片云前端仍有较大的碎片,即弹丸完全破碎临界速度在6.0~6.5 km/s间,取6.25 km/s为弹丸发生完全破碎的临界速度。对弹丸完全破碎时的临界速度和弹丸直径的关系进行拟合,绘制曲线如图4所示。由图4可见,弹丸完全破碎的临界速度随着弹丸直径的增加而增加,且呈近似正比关系。
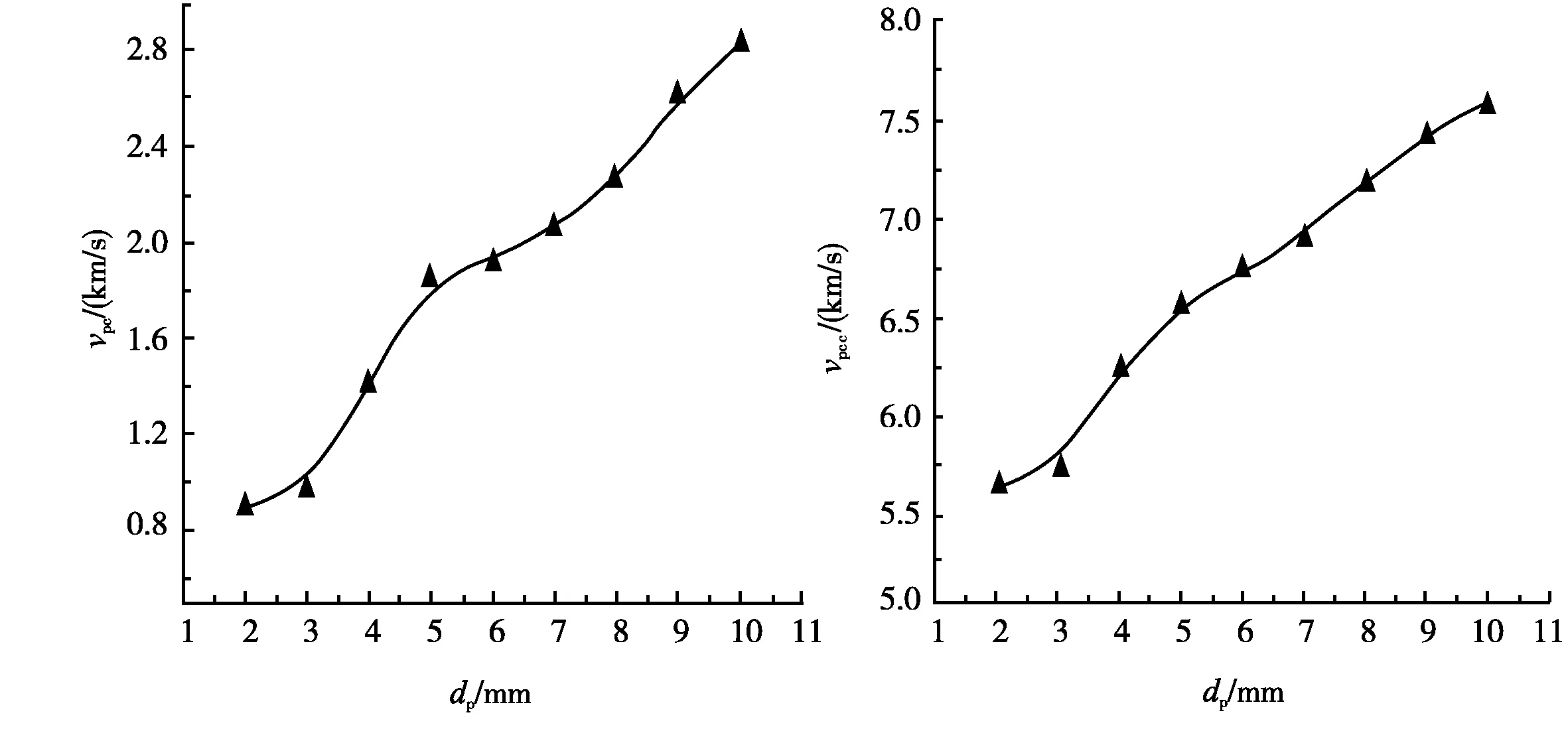
图3 vpc与dp的关系曲线 图4 vpcc与dp的关系曲线
2.2 弹丸破碎和完全破碎时的临界直径
确定不同撞击速度下弹丸发生破碎时的临界直径dpc和弹丸发生完全破碎时的临界直径dpcc。薄板厚度t取1.0 mm,弹丸撞击速度vp取1.0~4.0 km/s。图5给出了当撞击速度为2.5 km/s时不同弹丸直径下弹丸的破碎状态。由图5可见,随着弹丸直径的增加,弹丸越不容易发生破碎。

图5 不同弹丸直径下弹丸破碎情况
不同撞击速度下,弹丸发生破碎时的临界直径和完全破碎时的临界直径随撞击速度的变化曲线如图6、图7所示。由图6、图7可见,弹丸发生破碎的临界直径、弹丸发生完全破碎的临界直径均随着撞击速度的增加而增加。

图6 dpc与vp的关系曲线 图7 dpcc与vp的关系曲线
2.3 弹丸破碎和完全破碎时的临界板厚
确定不同弹丸撞击速度、弹丸直径下弹丸发生破碎时的临界板厚tpc和弹丸发生完全破碎时的临界板厚tpcc。图8给出了当撞击速度为2.0 km/s,弹丸直径为6.0 mm时在不同的薄板厚度下弹丸的破碎状态。由图8可见,随着板厚的增加,弹丸越容易发生破碎。

图8 不同板厚下弹丸破碎状态
计算弹丸直径dp为4.0 mm时,不同撞击速度下弹丸发生破碎时和完全破碎时的临界板厚,拟合曲线如图9和图10。由图9、10可见,随着撞击速度的增加,弹丸破碎时的临界板厚和完全破碎时的临界板厚均逐渐减小。
计算弹丸撞击速度vp为2.5 km/s时,不同弹丸直径下弹丸发生破碎时和完全破碎时的临界板厚,并拟合曲线如图11和图12。由图11、12可见,随着弹丸直径的增加,弹丸破碎时的临界板厚和完全破碎时的临界板厚逐渐增加,并近似呈正比关系。

图9 tpc与vp的关系曲线 图10 tpcc与vp的关系曲线 图11 tpc与dp的关系曲线 图12 tpcc与dp的关系曲线
3 结论
采用SPH方法拟合了弹丸破碎状态特性的曲线,可得出如下结论:
(1)弹丸撞击速度越大,撞击后弹丸破碎的小碎片越细化;且弹丸发生破碎和发生完全破碎时的临界速度均随着弹丸直径的增加而增加,并近似呈正比关系。(2)弹丸直径越大,弹丸越不易破碎;且弹丸发生破碎和发生完全破碎时的临界直径均随着撞击速度的增加而增加。(3)随着薄板板厚的增加,弹丸越容易发生破碎;弹丸发生破碎和发生完全破碎时的临界板厚随着撞击速度的增加而减小,随着弹丸直径的增加而增加,并近似呈正比关系。
